当前位置：文档之家 › 2流体静力学

2流体静力学

  • 格式：ppt
  • 大小：2.17 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

工程流体力学第2章流体静力学

工程流体力学第2章流体静力学

① 沿任意方向 ② 沿外法线方向
有切向分力 流体受拉力
都将破坏流体平衡。
这与静止前提不符，故假设不成立，则原命题成立。
①
②
4
第2章 流体静力学
特性二、静止流体中任何一点上各个方向的静压力大小相等，与作用面方位无关。
证明：采用微元体分析法 ① 取微单元体
在静止流体中，在O点附近取出各边长分别 为dx、dy、dz的微小四面体OABC。相应坐标 轴为x、y、z。
第2章 流体静力学
流体静力学：研究流体在静止状态下的平衡规律及其应用。 静止：流体质点相对于参考系没有运动，质点之间也没有相对运动。 静止状态包括两种情况： 1、绝对静止：流体整体对地球没有相对运动。
2、相对静止：流体整体对地球有运动，但流体各质点之间没有相对运动。
举例：
绝对静止
等加速水平直线运动 等角速定轴转动
2
第2章 流体静力学
§2.1 流体静压力及其特性
1、静压力的概念
（1）静压力：静止流体作用在单位面积上的压力，称为静压力，或静压强。记作“p”
一点的静压力表示方法：
设静止流体中某一点m，围绕该点取一微小作用面积A，其上压力为P，则： 平均静压力： p P
A
m点的静压力：p lim P
单位：
A0 A
m
国际单位：Pa
物理单位：dyn/cm2
工程单位：kgf/m2
混合单位：1大气压（工程大气压） = 1kgf/cm2
（2）总压力：作用在某一面积上的总静压力，称为总压力。记作“P”
单位：N
3
第2章 流体静力学
2、静压力的两个重要特性
特性一、静压力方向永远沿着作用面内法线方向。

2 流体静力学

2 流体静力学

思考题及答案一、选择 ............................................................1 二、例题 .............................................................6 三、问答 .. (25)一、选择问题1：比较重力场（质量力只有重力）中，水和水银所受的单位质量力f 水和f 水银的大小？ A. f 水<f 水银； C. f 水>f 水银；B. f 水=f 水银； D 、不一定。

问题2：试问自由落体和加速度a 向x 方向运动状态下的液体所受的单位质量力大小（f X . f Y . f Z ）分别为多少？自由落体：X ＝Y=0,Z=0。

加速运动：X=-a,Y=0,Z=-g 。

算一算：1.如图所示的密闭容器中，液面压强p 0＝9.8kPa ，A 点压强为49kPa ，则B 点压强为39.2kPa ,在液面下的深度为3m 。

问题：露天水池水深5m处的相对压强为：A. 5kPa；B. 49kPa；C. 147kPa；D. 205kPa。

问题1：仅在重力作用下,静止液体中任意一点对同一基准面的单位势能为_______？A.随深度增加而增加； C.随深度增加而减少；B.常数； D.不确定。

问题2：试问图示中A、B、C、D点的测压管高度？测压管水头？（D点闸门关闭，以D点所在的水平面为基准面）A:0m，6mB:2m，6mC:3m，6mD:6m，6m问题：某点的真空度为65000 Pa，当地大气压为0.1MPa，该点的绝对压强为：A. 65000P a；B. 55000P a；C. 35000P a；D. 165000P a。

问题：绝对压强pabs 及相对压强p、真空度pv、当地大气压pa之间的关系是：A. pabs =p+pv；B. p=pabs +paC. pv = pa-pabsD. p=pabs +pa问题1：金属压力表的读数值是：A.绝对压强； C.绝对压强加当地大气压；B.相对压强； D.相对压强加当地大气压。

第二章流体静力学

第二章流体静力学

dy → 0, p y = pS 当四面体向A点收缩时，
同理 px = pz = pS
§2.2静力学基本方程（Euler静平衡方程）：
取一个矩形微元六面体，其六个面分别与 坐标轴平行，设微元中心处的压强为 p。 由于 这是个微小体积，因此认为六个面上的压强各 自均匀分布，常用面上中心来做代表。

而面上中心处的压强又可以围绕六面体 中心做Taylor展开。展开式忽略二阶以上 的高阶量，有
1 ⎞ ⎛ p A = p⎜ x + dx ⎟ 2 ⎠ ⎝
p A = p + 0.5(∂p ∂x )dx
p B = p − 0.5(∂p ∂x )dx

这样，垂直于x轴的两个面上的表面力分 别为
[ p + 0.5(∂p ∂x )dx ]dydz [ p − 0.5(∂p ∂x )dx ]dydz
§2.3重力作用下静止流体内部的压强分布 [均匀液体的压强分布] 根据Euler静平衡方程 可以得到：
p = p0 + γh
第一部分是自由面上的压强，第二部分称 为剩余压强。
p = p0 + γh = γ ( p0 γ + h )
这种做法，称为虚水面方法。
[连通器] （ 1 ）同种液体，表面自由压强相等。则两液面 等高，任一等高度的面上均为等压面。 （ 2 ）同种液体，但表面自由压强不等。则自由 压强大者，液面低。 （3）不同液体（不相混）。密度大者液面低。
F = ∫ ρf dV
V
2、表面力——一个流体体积的表面上，受 到其他部分的流体或与之相接的固体的 作用力。这种力，只是作用在体积的表 面上而没有作用到体积内部的流体质点 上。 通常可以把表面力分解为法向的和 切向的分量，分别称为法向力和切向力。 单位面积上则称为法向应力和切应力。

2 流体静力学

2 流体静力学

其全微分式 Xdx Ydy Zdz 1 (p dx p dy p dz)
x y z
dp ( Xdx Ydy Zdz)
§2.2 流体平衡微分方程
§2.2.3 等压面
等压面：静止流体中压强相等的点连接成的面（平面或曲面）。
根据欧拉平衡微分方程的全微分表达式
点上各方向的静压强大小相等。
证明如下：
在流体中去一个特殊四面体作为研究对象，如图所示
px 为作用在ΔODB面上的静压强；
z D
py
py 为作用在ΔODC面上的静压强； px dz
pn
pz 为作用在ΔOBC面上的静压强； pn 为作用在ΔDBC面上的静压强。
dy o dx C x B
y
pz
§2.1 静止流体中压强的特性
1. 静压力 静止（或处于相对平衡状态）流体作用在与之接触的表面上的
压力称为静压力或压力。
2. 静压强
取微小面积 ，A令作用于
所受的平均静压力为
静压强
p lim F A0 A
的静A 压力为 ，则F 面上单A位面积
p F A
3. 动压强
处于流动状态的流体内部的压强称为流体动压强。
解:
pA pa m g (1 2 ) g (3 2 ) m g (3 4 ) g (5 4 )
pa m g (1 2 3 4 ) g (3 2 5 4 )
pa m g(1.8 0.6 2.0 1.0) g(2.0 0.6 1.5 1.0)
pa 13.6 103 9.81 2.2 103 9.811.9
故
pAabs 98.1 274.9 373KN / m2

第一章 2 流体静力学 流体流动中的守恒原理

第一章 2 流体静力学 流体流动中的守恒原理

即：
X − 1 ∂p = 0 ρ ∂x
类似地，在Ｙ、Ｚ方向：
Y − 1 ∂p = 0 ρ ∂y
Z − 1 ∂p = 0 ρ ∂z
这就是流体平衡微分方程式，也即欧拉平衡方程。
流体静力学方程
重力场中： X=Y=0，Z= - g 对连续、均质
∂p =0 ∂p =0 ρg + ∂p =0
∂x ∂y
∂z
ρg + dp = 0 dz
表压
绝对压
真空度
p2
大气压
绝对压
绝对真空
流体静力学方程
p − ∂p δ x ∂x 2
p + ∂p δ x (压强) ∂x 2
(p + ∂p δ x )(δ yδ z) (压力) ∂x 2
取立方微元体边长δx、 δ y、 δ z，其中心A点
压强为p，作用于此微元
体上的力有表面力和质量 力两种。以x方向为例：
静力学基本方程的应用回顾第一节体积力重力离心力表面力流体流动中的作用力压力绝压表压真空度液柱高度剪切力牛顿粘性定律粘度回顾1112流体静力学方程推导及讨论压力型式能量型式流体静力学方程的应用压力测量简单测压管原理性u形测压管回顾111213流体流动中的守恒原理流体流动基本方程流体动力学流体流动服从的守恒定律
7
1.3.2 机械能守恒——柏努利方程
1. 总能量衡算
1 p ,u ,ρ
1 11
1' z
1
0
q
e2 p ,u ,ρ
2 22
2'
z 2
h e 0'
衡算范围：1-1′、2-2′截面以及管内壁所围成的空间 衡算基准：1kg流体 基准面：0-0′水平面

第二章-流体静力学

第二章-流体静力学

第⼆章-流体静⼒学⼀、学习导引1、流体静⽌的⼀般⽅程（1）流体静⽌微分⽅程x p f x ??=ρ1，y p f y ??=ρ1，zpf z ??=ρ1 （2）压强微分)(dz f dy f dx f dp z y x ++=ρ（3）等压⾯微分⽅程0=++dz f dy f dx f z y x2、液体的压强分布重⼒场中，液体的位置⽔头与压强⽔头之和等于常数，即C pz =+γ如果液⾯的压强为0p ，则液⾯下深度为h 处的压强为h p p γ+=03、固体壁⾯受到的静⽌液体的总压⼒物体受到的⼤⽓压的合⼒为0。

计算静⽌液体对物⾯的总压⼒时，只需考虑⼤⽓压强的作⽤。

（1）平⾯壁总压⼒：A h P c γ= 压⼒中⼼Ay J y y c cc D += 式中，坐标y 从液⾯起算；下标D 表⽰合⼒作⽤点；C 表⽰形⼼。

（2）曲⾯壁总压⼒：222z y x F F F F ++=分⼒：x xc x A h F γ=，y yc y A h F γ=，V F z γ=4、难点分析（1）连通器内不同液体的压强传递流体静⼒学基本⽅程式的两种表达形式为C pz =+γ和h p p γ+=0。

需要注意的是这两个公式只适⽤于同⼀液体，如果连通器⾥⾯由若⼲种液体，则要注意不同液体之间的压强传递关系。

（2）平⾯壁的压⼒中⼼压⼒中⼼的坐标可按式Ay J y y c cc D +=计算，⾯积惯性矩c J 可查表，计算⼀般较为复杂。

求压⼒中⼼的⽬的是求合⼒矩，如果⽤积分法，计算往往还简便些。

（3）复杂曲⾯的压⼒体压⼒体是这样⼀部分空间体积：即以受压曲⾯为底，过受压曲⾯的周界，向相对压强为零的⾯或其延伸⾯引铅垂投影线，并以这种投影线在相对压强为零的⾯或其延伸⾯上的投影⾯为顶所围成的空间体积。

压⼒体内不⼀定有液体。

正确绘制压⼒体，可以很⽅便地算出铅垂⽅向的总压⼒。

（4）旋转容器内液体的相对静⽌液体随容器作等⾓速度旋转时，压强分布及⾃由⾯的⽅程式为c z gr p +-=)2(22ωγc gr z +=2220ω恰当地选取坐标原点，可以使上述表达式简化。

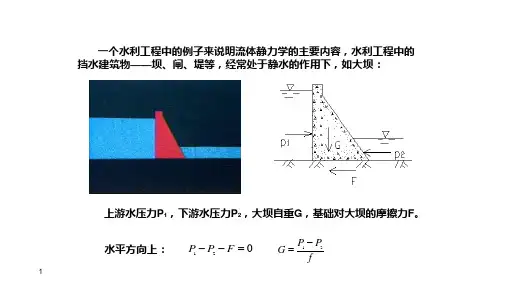
2 流体静力学

2 流体静力学
缺点：易受人为破坏、降雨量的影响、易淤堵
2 U形水银测压计 当被测点压强很大时，所需测压管很长，这时可以
改用U形水银测压计。
在U形管内，水银面N-N为等压面，p1=p2。 对测压计右支 对测压计左支 A点的绝对压强 A点的相对压强 式中， 与m分别为水和水银的密度。
3 差压计 差压计是直接测量两点压强差的装置。若左、右两容器
内各盛一种介质，其密度分别为 A和 。B 因c-c面是等压面，于是
pA AghA pB B ghB m gh pA pB m gh B ghB AghA hA s hB h
hA h hB s pA pB (m A )gh (B A )ghB Ags
流体静压强基本特性
特性一：静止流体只能承受压应力，压强的方向垂直并指向作用面。
用反证法来证明此特性： 取一块处于静止状态的流
体，若作用面AB上的应力p’ 的方向向外且不垂直于AB， 则可分解成法向应力pn和切向
应力 。
1）若存在 ，必然有流动，这与静止的前提不符， 0。 2）流体不能承受拉力，因此 p的方向必然是内法线方向，如图中的 p。
3
静压力与静压强
静压力：在平衡流体内部相邻两部分之间相互作用的力 或流体对固体壁面的作用力称为压力，常以字母F表示。
静压力：取微小面积A ，令作用于A 的静压力为FP，则
单位面积所受的平均静水压力为 p FP /。A
静压强： p lim FP A0 A
静压力FP的单位：牛顿(N)； 静压强 p 的单位：牛顿/米2(N/m2)，又称为“帕”(Pa)。
代入平衡微分方程
dp ( fxdx f ydy fzdz)
p0

流体流动2—流体静力学

流体流动2—流体静力学

2 x
2 x
各项均除以微元体的流体质量xyz
可得：
1 p
X
0
x
Байду номын сангаас
X 1 p 0
x
同理 y方向
Y 1 p 0
y
z方向
Z 1 p 0
z
…欧拉平衡方程
若将该微元流体移动dl距离
此距离对三个坐标轴的分量为dx、dy、dz
dp gdz 0

dp


g

dz

0
设流体不可压缩，即密度ρ与压力无关，可将上
式积分得：
p gz 常数 或 p gz 常数

物理意义为：任一平面上，静压强与ρgz的和为
一常数
对于静止流体中任意两点1 和2，

p1


gz1
或p2

gz2
p2 p1 g(z1 z2 ) p1 gh
1.2 流体静力学
Fluid statics or Hydrostatics
流体静力学：研究流体在重力和压力作用 下的规律
特点：流体处于相对静止状态，即流体在 外力作用下达到平衡的状态
重力可以看作不变，因此变化的是压力 实质：研究的是静止流体内部压强变化的
规律
一、静压强static pressure在空间的 分布
dp Xdx Ydy Zdz


即流体平衡的一般表达式
等式两边分别表示压力和体积力所作的功
2、平衡方程在重力场中的应用： 流体静力学基本方程式
如流体所受的体积力仅
为重力，并取z轴方向与

第二章流体静力学

第二章流体静力学

当四面体的体积趋于零时，可证得px= py=pz=pn
即
p=p(x,y,z)
§2-2 流体的平衡微分方程及积分
一、流体的平衡微分方程
在平衡流体中取如图所示微小正交六面体。分析六面
体在x、y、z方向所受外力，列平衡方程，整理化简得
fx
1
p x
0
fy
1
p y
0
1 p
fz z 0
上式也可用矢量方程表示：
虚压力体：压力体和液体在受压曲面的异侧， Pz向上。
A
A
B
B
例4：试绘制图中abc曲面上的压力体。如已知曲面abc为半圆 柱面，宽度为1m，d=3m，试求abc柱面所受静水压力的水平分 力Px和竖直分力Pz 。
a
d d/2
b 水
水 c
[解] 因abc曲面左右两侧均有水的作用，故应分别考虑。
考虑左侧水的作用
故得欧拉平衡微分方程综合式（即全微分形式）
dp ( f xdx f ydy f z dz)
四.等压面
1.定义： p=C或dp=0的平面或曲面。
2.等压面微分方程
f xdx f y dy f z dz 0
或
f•
ds
0
3.等压面的性质
(1)等压面与等势面重合;
(2)等压面恒与质量力正交。
其作用点为通过体积重心所引出的水平线与受压面的交点D。 当相对压强分布图为三角形时，D点位于自由液面下(2h)/3处。
对于相对压强分布图为梯形情况，可将其分解成三角形和矩 形两部分进行计算后，最后利用合力矩定理求总压力作用点。
例3.铅垂放置的矩形平板闸门，面板后布置三根横梁,各横梁受 力相等,已知闸门上游水头H=4m，试求： （1）每根横梁所受静水总压力的大小； （2）各横梁至水面的距离。

流体静力学

流体静力学

p
z
p
C

p
—压强水头(the pressure head)

z—测压管水头(piezometric head)
测压管(the piezometer tube) 是一端 和大气相通，另一端和液体中某一 点相接的管子。 p z C

表示同一容器的静止液体中，所有 各点的测压管水头均相等。 This shows that for incompressible fluid at rest the summation of the elevation z at any point in a fluid plus the pressure head at that point is equal to the sum of these two quantities at any other point. The significance of this statement is that, in a fluid at rest with an increase in elevation, there is a decrease in pressure head and vice versa.
第二章 流体静力学
(Chapter 2 Fluid Statics) • 流体静力学研究流体处于静止或相对静止状态下的平 衡规律及其应用。 • 静止的含义：流体的静止状态是一个相对的概念，指 流体质点之间不存在相对运动，或流体质点相对于参 考系没有相对运动，处于相对平衡状态。 • 静止流体的应力特征：当流体处于相对静止，质点之 间无相对运动的条件下，粘性将无从表现，流体内部 不存在切应力，而只存在正应力（亦即法向应力）。 事实上，由于流体不能承受拉应力，故流体质点间或 流体接触面之间的作用是通过压应力的形式来体现的。 因此，根据力学平衡条件研究静压强的空间分布规律， 确定各种承压面上静压强产生的总压力，是流体静力 学的主要任务。

工程流体力学2-流体静力学

工程流体力学2-流体静力学
该闸门上所受静水总压力的大小为246kN， 方向向右，作用点在水面下8.03m处。
流体力学
2.7 作用在曲面上的液体总压力
实际工程中经常遇到受压面为曲面的情况，如
弧形闸门 拱堤堤面
贮水池壁面 水管管壁
U形渡槽，等
本节仅对工程中应用最多的二向曲面（即具有 平行母线的柱面）进行讨论。
p 表面力： pb dydz pc dydz dxdydz x
质量力：
f x dxdydz
据
流体力学
p F x 0 : f x d x d y d z d xdydz 0 x
2.1 流体平衡微分方程式
推导
p p dx dydz x
p0 h1
相对压强：
p0 abs pa 4900 g (h2 h1 ) 4900 1000 9.8 (0.5 1.5) 4900 Pa
A
绝对压强：
流体力学
p 0 abs 4900 p a 4900 98000 93100 Pa
故欧拉平衡微分方程可以写成全微分形式
dp ( f x dx f y dy f z dz )
通常作用在流体上的单位质量力是已知的，利用上式 便可求得流体静压强的分布规律。
流体力学
第二章 流体静力学
2.2 等压面

定义：在流场中，压强相等（dp=0）的各点组成的面。 微分方程：
由定义得：
流体力学
2.1 流体平衡微分方程式
推导
1 p dx dydz p 2 x
b
a p(x,y,z)
c
1 p dx dydz p 2 x

第二章 流体静力学

第二章 流体静力学

A
P P A
P dp P lim A0 A dA
流体静压力和流体静压强都是压力的一种度量，它们的区 别仅在于前者是作用在某一面积上的总压力，而后者是作 用在某一面积上的平均压力或某一点的压强。
§2.1 流体静压强及其特性
2.1.2 流体静压强的特性 特性一：流体静压强的作用方向沿作用面的内法线方向。
1
第二章 流体静力学
§2.1 流体静压强及其特性
§2.2 重力场中流体的平衡 §2.3 压强的计算基准和度量单位
§2.4 液柱式测压计
§2.5 静止液体作用在固体壁面上的总压力 §2.6 流体平衡微分方程
§2.7 液体的相对平衡
§2.1 流体静压强及其特性
2.1.1 流体静压强 当流体静止或者相对静止时，流体的压强称为流体的静压强。
2.2.3 液体静压强分布图
p p0 gh
1.ρgh部分的绘制
P0
D
A
= gh 设 P＇
’ 对于A点： P A = ghA 0
’ 对于B点： PB = ghB
P
E
C
2. P0部分的绘制
P 0
ghB
B
PB P 0 ghB
h
根据静压强等值传递规律，P0部分等值的传递到 受压面任意点上去。
如果A、B两处为同种液体：
A B
pA pB g (h2 h1 ) g gh3
1-2为 等压面
如果A、B两处为同种气体：
pA pB g gh3
§2.4 液柱式压差计
2.4.3 倾斜式微压计
h l sin
p ＇g (h h)
A1 h A2l

第二章 流体静力学

第二章 流体静力学
2、作用于六面体的质量力 x轴向
X dxdydz
x轴向的平衡 1 p 1 p (p dx)dydz ( p dx)dydz X dxdydz 0 2 x 2 x
X
p 0 x
同理
p Y 0 y p Z 0 z
流体平衡微分方程式 （欧拉平衡方程）
第二节 流体静压强的分布规律
三、气体压强计算
前述规律，虽然是在液体的基础上提出来的，但对于不可 压缩气体仍然适用。 由于气体密度很小的特点，在高差不是很大的情况下，气 柱产生的压强很小，因而可以忽略ρg h的影响，即 p= p0 上式表明空间各点气体压强相等，例如液体容器、测压管、 锅炉等上部的气体空间，就认为各点的压强是相等的。
第一节 流体静压强及其特性
二、流体静压强的特性
（1）静压强的垂向性。 流体静压强总是沿着作用面 的内法线方向。 （2）静压强的各向等值性。 在静止或相对静止的流体中，任一点的流体静压强的大小与 作用面的方向无关，只与该点的位置有关，即同一点上各个 方向的流体静压强大小相等。
第一节 流体静压强及其特性
第七节 液体平衡微分方程
p 0 x p Y 0 y p Z 0 z
X
指出流体处于平衡状态时，作用于 流体上的质量力与压强递增率之间 的关系。它表示单位体积质量力在 某一轴的分力，与压强沿该轴的递 增率相平衡。
1 p x 1 p Y y 1 p Z z X
水头。 p Z ：测压管水面相对于基准面的高度，测压管水头。 g
所谓测压管是一端和大气相通，另一端和液体中某一点相 接的管子。 两水头相加等于常数，表示在同一容器的静止液体中所有 各点的测压管水面必然在同一水平面上。
第二节 流体静压强的分布规律

流体力学第02章流体静力学

流体力学第02章流体静力学

于质量力只有重力的同一种连续介质。对不连续液体或
一个水平面穿过了两种不同介质，位于同一水平面上的
各点压强并不相等。
二 气体压强的分布（不讲） （不讲就不考）
三 压强的度量--绝对压强与相对压强
1、 绝对压强
设想没有大气存在的绝对真空状态作为零点计量的压 强，称为绝对压强。总是正的。
2、 相对压强
解：相对静水压强：
p pabs pa p0 gh pa
代入已知值后可算得
h ( p p0 pa ) (9.8 85 98) / 9.8 2.33m
g
例： 如图，一封闭水箱，其自由面上气体压强为
25kN/m2，试问水箱中 A、B两点的静水压强何处为大？
已知h1为5m，h2为2m。 解：A、B两点的绝对静水
因水箱和测压管内是互相连通的同种液体故和水箱自由表面同高程的测压管内n点应与自由表面位于同一等压面上其压强应等于自由表面上的大气压强即ghgh11测压管测压管若欲测容器中若欲测容器中aa点的液体压强点的液体压强可在容器上设置一开口细管可在容器上设置一开口细管
第二章 流体静力学
流体静力学的任务：是研究液体平衡的规律及其
p
g
p0
g
得出静止液体中任意点的静水压强计算公式：
p p0 gh
式中
h z0 z ：表示该点在自由面以下的淹没
深度。
p0 ：自由面上的气体压强。
静止液体内任意点的静水压强有两部分组
成：一部分是自由面上的气体压强P0，另一部分 相当于单位面积上高度为h的水柱重量。
(a)
(b)
(c)
淹没深度相同的各点静水压强相等，只适用
pA gLsin
当被测点压强很大时：所需测压管很长，这时可以改 用U形水银测压计。

第2章 流体静力学

第2章 流体静力学

第2章 流体静力学本章提要研究内容：静止流体的力学规律以及这些规律在工程实际中的应用。

静止含义：以地球作为惯性参考坐标系绝对静止：流体相对于惯性坐标系静止 相对静止：流体相对于非惯性参考坐标系静止适用范围：实际流体、理想流体都是适用的。

【学习重点、难点】 重点：1. 静压强及其特性，点压强的计算，静压强分布。

2. 作用于平面上液体总压力。

3. 作用于曲面上液体总压力，压力体的画法。

难点：1. 应用静力学基本定律计算作用在平面、曲面上的总压力；2. 不同高度的液体对固体壁面总压力的计算。

0=μ0=τ§2.1 流体静压强的特性2.1.1静压强定义及特性流体处于静止状态时，流体的压强称为流体的静压强静止液体只能承受压力，几乎不能承受拉力，它与固体比较具有两个明显的特性：1.流体静压强方向与作用面相垂直，并指向作用面的内法线方向。

证明：假设：在静止流体中，流体静压强方向不与作用面相垂直，与作用面的切线方向成α角则存在切向压强pt这与假设静止流体相矛盾2.静止流体中任意一点流体压强的大小与作用面的方向无关，即任一点上各方向的流体静压强都相同。

证 明：取一微元四面体的流体微团ABCD ，边长分别为dx ，dy 和dz 由于流体处于平衡状态，故作用在其上的一切力在任意轴上投影的总和等于零。

流体微团受力分析：x 方向受力分析表面力：nz y xp p p p ===∑=0x F ∑=0yF∑=0zFzy x p x P d d 21=ααcos dcos nA np n P =zy A n d d 21cos d =α质量力：因为流体平衡:在轴方向上力的平衡方程为把 P x ，P n 和W x 的各式代入得化简得由于等式左侧第三项为无穷小，可以略去，故得几点说明:（1） 静止流体中不同点的静压强一般是不等的，是空间坐标的连续函数。

同一点的各向静压强大小相等。

z y n p n P d d 21cos =αXdxdydzX dxdydz ρρ11F x ∙⨯=∑=0xFcos =+-x n x W P P α0d d d 61d d 21d d 21=+-z y x X z y p z y p n x ρ0d 31=+-x X p p n x ρnx p p =（2） 运动状态下的实际流体，流体层间若有相对运动，则由于粘性会产生切应力，这时同一点上各法向应力不再相等。

第二章流体静力学

第二章流体静力学

二、液体随容器作等角速度旋转运动
z 建立如图所示动坐标系 ω
X = ω 2 x, Y = ω 2 y , Z = − g
p0
dp = ρ (ω xdx + ω ydy − gdz )
2 2
y
o
A g
x
p = ρ( = ρ(
ω 2 x2
2
+
ω 2 y2
2
− gz ) + C
o x y
x
y r A
ω y
p / ρg
能；
C 表示单位重量流体所具有的总势能，简称总能。 表示单位重量流体所具有的总势能，简称总能。
在重力作用下， 在重力作用下，静止流体中各点的单位重量流体的总 势能是相等的。 势能是相等的。
三、流体静力学基本方程的几何意义
单位重量流体具有的能量用液柱高度来表示称为水头。 单位重量流体具有的能量用液柱高度来表示称为水头。 水头 表示该点到基准面的高度，称为位置水头， z 表示该点到基准面的高度，称为位置水头，简称位水
hC 平面形心点的淹没深度
A
PyD = ∫ ydP =ρ g sin α ∫ y 2 dA = ρ g sin α I x
∂p dx pA = p − ∂x 2 ∂p dx pB = p + ∂x 2
1 ∂p p− dx dydz 2 ∂x
A
C p
B
1 ∂p p+ dx dydz 2 ∂x
½ dx
图2－4
由于微六面体处于平衡状态， 由于微六面体处于平衡状态，所以由平衡条件得
一、流体平衡微分方程
在静止的流体中取一微六面体，如图2-4所示。取六面 在静止的流体中取一微六面体，如图2 所示。 体内中心点C点，设C点的静压强为 p ，过C点作轴的平行线 体内中心点C 交左右侧面分别为A 将静压强按泰勒级数展开， 交左右侧面分别为A、B点，将静压强按泰勒级数展开，并略 去高阶微量， 去高阶微量，则
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dp Zdz gdz 积分 p gz c
p1
g
z1
p2
g
z2
c
单位重量能量
p1 gz1 p2 gz2 c （Pa）
相对平衡
1.等加速直线运动流体的平衡
z x
由 dp Xdx Ydy Zdz
ao
X a（惯性力） Y 0,Z g
2 x
X
1
p x
0
Y
1
p y
0
Z
1
p z
0
欧拉平衡微分方程式
表明了单位质量流体所 承受的质量力和表面力沿 各轴的平衡关系。
2流体静力学
将欧拉平衡方程式分别乘以dx、dy、dz，并相加
p dx p dy p dz ( Xdx Ydy Zdz)
x
y
z
dp ( W dx W dy W dz)
面，使留在液面以下部分物体所排开的液体重量恰好等于 物体的重力为止，称为浮体。
2.5.1 浮体与潜体的稳定性
平衡条件：合力为零，合力矩为零
如果要求浮体和潜体在液体中不发生转动，还 必须满足重力和浮力对任何一点的力矩的代数和为 零，即重心 C 和浮心B 在同一条铅直线上。但这种 平衡的稳定性（也就是遇到外界干扰，浮体和潜体 倾斜后，恢复到原来的平衡状态的能力）取决于重 心C和浮心B在同一条铅直线上的相对位置。
2.流体静力学
2.1 流体静压强及其特性 2.2 流体的平衡微分方程 2.3 流体静力学基本方程 2.4 静止流体对壁面的总压力 2.5 浮体与潜体
习题
流体静力学是研究流体平衡以及 全部或部分浸在流体中的固体平衡的 力学。
流体质点与质点之间，以及流体 质点与固体接触面之间没有相对运动 的流体，都称为平衡流体或相对平衡 流体。
r 0,z 0, p pa 0
p
0
dp
0r 2 rd r
0z
gdz
p
2r 2
2
gz
在自由面： p 0
z 2r2
2g
z
o
r
ω2r g
等压面为旋转抛物面
2.4 静止流体对壁面的总压力
1.作用在平面上的总压力
（1）总压力
dP pdA
ghdA gy sindA
P dP g sin A ydA g sinyc A ghc A pc A
dPz dPsin ghdAsin ghdAx
Pz dPz gAz hdAx gV
V——压力体体积
Ax Az
Pz
（3）合作用力大小
P Px2 Py2 作用点通过压力体体积的形心
（4）合作用力方向
与水平面夹角 tg Pz
Px
压力体由以下各面围成：
（a）曲面本身；
压
（b）通过曲面周界的铅垂面；
2流体静力学
(1)流体静压强的方向必然重合于受力面的内 法线方向。
(2)平衡流体中任意点的静压强值只能由该点 的坐标位置来决定，而与该压强的作用方
向无关。即：平衡流体中各点的压强 p 只 是位置坐标 ( x, y, z ) 的连续函数，与作用
方向无关。即：p f (x, y, z)
2流体静力学
干扰力矩
干扰力矩
CG
CG
CG
随遇平衡
浮心在上重心之 上，稳定平衡
干扰力
C G
恢复力偶
C G
潜体的重心在浮心之上
干扰力矩
恢复力矩
M
G
G
C
倾覆力矩 CM
M－定倾中心
浮体与潜体的稳定性
1. 当重心在浮心之下时，潜体处于稳定平衡。
潜 体 2. 当重心在浮心之上时，潜体处于不稳定平衡。
3. 当重心与浮心重合时，潜体处于随遇稳定平衡。
力
（c）自由液面或者延续面
体
的
实压力体
作
法
虚压力体
p 水平压力
压力体
V
F= gyVsindA
2流体静力学
一切浸没于液体中或漂浮于液面上的物体都受到两个力 作用：一个是垂直向上的浮力，其作用线通过浮心；另一个 是垂直向下的重力G，其作用线通过物体的重心。 根据重力G与浮力Pf的大小，物体在液体中将有三种不同的 存在方式： 1．重力G大于浮力Pf ，物体将下沉到底，称为沉体； 2．重力G等于浮力Pf ，物体可以潜没于液体中，称为潜体； 3．重力G小于浮力Pf ，物体会上浮，直到部分物体露出液
x
y
z
X W ;Y W ; Z W
x
y
z
p W c
c p0 W0
p p0 (W W0 )
在平衡流体中，压强相等的各点所组成的面称为等压面。
Xdx Ydy Zdz 0
特征：（1）等压面为等势面（等高面）。 （2）等压面是一个垂直于质量力的面。
重力作用下的液体压强分布规律
Z g
（2）压力中心
dM dPy
M dM dPy PyD y sindAy yC sin AyD
ghdAy ghC AyD
y2dA yC AyD
Ix y2dA ——受压面A对ox轴的面积矩（惯性矩）
I x IC yC2 A
I y2A
y C
C
D
yA
C
压力中心始终在形心之下。
2.作用在曲面上的总压力
（1）总压力的大小和方向
Px
a 水平方向的作用力
dPx dP cos ghdAcos ghdAz
Px dPx gAz hdAz ghC Az pC Az
hdAz ghC Az pC Az
大小、作用点与作用 在平面上的压力相同
Ax Az
（2）垂直方向的作用力
g
a
边界条件： x 0,z 0, p pa
pab pa
dp
0x
adx
0z
gdz
pab pa ax gz
相对压强： p ax gz
在自由面： p 0 z a x g
等压面为倾斜平面
2.匀速圆周运动流体的平衡
由 dp Rdr Zdz
R 2r（惯性力） Z g
边界条件：
潜体和浮体在静止流体中的平衡条件：
浮力与重力相等，作用在同一 铅垂直线上。 (合力与合力矩为零)
C G
浮体
C G
潜体
潜体的重心在浮心之下
干扰力矩
干扰力矩
C
C
C
G
G
G
恢复力矩
恢复力矩
稳定平衡
潜体的重心在浮心之上
干扰力矩
A 干扰力矩
G
G
G
C
C
C
倾覆力矩 B
C GC
G
不稳定平衡
倾覆力矩 B
C G
A
潜体的重心与浮心重合
在平衡流体中取 六面体流体微团，如 图示。微团在质量力 和表面力的作用下处 于平衡状态。
分析X 坐标轴方
向上各力的分量
质量力：dGx dxdydzX
表面力：
pA
p
1 2
p x
dx
pB
p
1 2
p x
dx
( p 1 p dx)dydz ( p 1 p dx)dydz dxdydzX 0
2 x