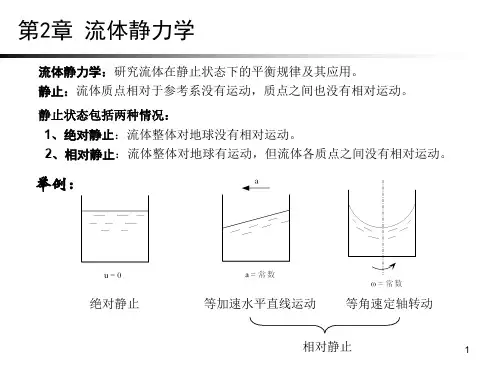
第二章流体静力学流体静力学研究流体在静止状态下的力学规律。
由于静止状态下，流体只存在压应力，简称压强，因此，流体静力学这一章以压强为中心，阐述静压强的特性，静压强的分布规律，以及作用面上总压力的计算。
1静止流体中应力的特性2流体平衡微分方程3重力场中流体静压强的分布规律4流体的相对平衡5液体作用在平面上的总压力6液体作用在曲面上的总压特性一：应力的方向沿作用面的内法线方 向。
特性二：静压强的大小与作用面方位无关。
1 •欧拉方程2.全微分方程自然界常见的质量力是重力，因此，在 流体平衡一般规律的基础上，研究重力作用下流-丄空=()p dx丄丝=0 p Z -丄空二 P dz体静压强的分布规律，更有实用意义。
等压而:压强相等的空间点构成的而性质：Ho基本方程：1卩=Po + pghpg气体压强的分布1・对流层、50256zp = 101 .3 1 --- - KPaI 44300 丿2.同温层<11000 一p = 22 .6 exp ----------6334 丿压强的度量1・绝对压强和相对压强绝对压强以无气体分子存在的完全真空为基准起算的压强。
相对压强是以当地大气压为基准起算的压强。
P = Pabs一P2 •真空度当绝对压强小于当地大气压，相对压强便是负值，又称负压，这种状态用真空度来度量。
［例2・1］立置在水池中的密封罩（如图2・6）所示，求罩内A、B、C三点的压强。
1・测压管高度、测压管水头Z 称为位置高度或位置水头。
称为测压管高度或压强水头。
"嬴称为测压管水头。
2 •真空高度pg［例2・2］密闭容器（图2-9）,侧壁上方装有U形管水银测压计，读值hP=20cm。
试求安装在水面下3.5m处的压力表读值。
［例2・3］用U形管水银压差计测量水管A、B 两点的压强差（图2-10） o已知两测点的高差△ z=0.4m,压差计的读值hP = 0.2 m o 试求A、B两点的压强差和测压管水头差。
