(优选)等高线地形图的计算

等高线计算公式【原创版】目录1.等高线的定义和作用2.等高线的计算公式3.计算公式的应用示例4.结论正文1.等高线的定义和作用等高线是地图学中的一种符号，用于表示地形高度相同的点。

在地图制作和地理研究中，等高线起着重要作用，能够直观地反映出地形地貌的特点。

通过观察等高线，我们可以了解地区的海拔高度、坡度、方向等信息。

2.等高线的计算公式等高线的计算公式基于地图学原理和数学方法。

在平面上，等高线可以通过以下公式计算：h = (R * ln(tan(α/2))) / (2 * Δh)其中，h 表示等高线的海拔高度，R 表示地球半径，ln 表示自然对数，tan 表示正切，α表示地形角度，Δh 表示等高线间隔。

3.计算公式的应用示例为了更好地理解等高线的计算公式，我们可以通过一个实际应用示例来说明。

假设我们要绘制一个 10 公里×10 公里的区域地图，地图上的等高线间隔为 100 米，地形角度为 45 度，地球半径为 6371 公里。

我们可以使用以下步骤计算等高线的海拔高度：步骤 1：将地图上的距离转换为地球表面的距离。

在这个例子中，10 公里在地球表面上对应的距离为：10km * cos(45°) = 7.07km步骤 2：根据地球半径和地图上的距离，计算出等高线的海拔高度：h = (6371km * ln(tan(45°/2))) / (2 * 100m) = 70.7m因此，在这个例子中，等高线的海拔高度为 70.7 米。

4.结论等高线的计算公式是地图学中一个重要的概念，可以帮助我们了解地形地貌的特点。

等高线地形图中的相关计算”★★★★○○○1．估算某地形区的相对高度的方法(1)公式计算法：如图所示,求A、B两点间的相对高度:A、B两点之间有3条等高线，等高距为100 m，利用公式（n－1)d m＜H＜(n＋1）d m。

可得A、B两点间的相对高度为200 m＜H＜400 m。

（2）直接计算法：根据图中各点的海拔计算相对高度，如图中A点海拔为300~400 m，B点海拔为0～100 m，则A、B的相对高度为(300－100）m＜H＜（400－0）m。

2．闭合等高线区域内高度(海拔)的判断位于两条等高线之间的闭合区域，如果其值与两侧等高线中的较低值相等，则闭合区域内的高度(海拔)低于较低值等高线的值；如果闭合等高线的值与两侧等高线中的较高值相等，则闭合区域内的高度(海拔)高于较高值等高线的值，即“大于大的，小于小的”。

如下表：大于大的相邻等高线之间的闭合区域,海拔不在两条等高线的数值之间，如A高度(海拔）高于200米，而B低于100米(大于大的，小于小的）小于小的高考试题中多以等高线为背景对等高线地形图的综合判读和相关计算进行考查.等高线地形图上，等高线闭合且等高线数值中间高四周低则为山顶，两山顶之间相对低洼的部位为鞍部，等高线闭合且等高线数值中间低四周高则为盆地，等高线向海拔低处凸为山脊，等高线向海拔高处凸为山谷，等高线重合的地方为陡崖。

陡崖相对高度的计算公式为，（n－1)d≤△H＜(n＋1）d(n为陡崖处重合的等高线的条数，d为等高距）。

等高线的递变规律，按某一递增或递减的顺序变化。

d为一处洼地，故d周围闭合等高线数值应和两侧等高线中较小的相等。

依据“大于大的,小于小的"规律判断即可。

下图示意某小区域地形。

图中等高距为100m，瀑布的落差为72 m.据此回答(1)～(2）题.(1)Q地的海拔可能为( )A．90 m B．230 mC．340 m D．420 m(2）桥梁附近河岸与山峰的高差最接近( ）A．260 m B．310 mC．360 m D．410 m【答案】(1)D (2）C【易错剖析】此题易错点是对瀑布的落差为72米的理解，瀑布位于桥梁之上，学生容易忽略这一点，而是简单的套用公式（n－1)d＜H＜(n＋1)d，这就要求学生做题时，需要结合试题的实际情况，明白不同地理事物的相对位置。

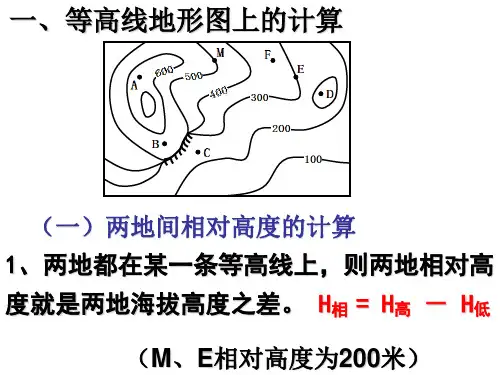
方法技巧：如何进行等高线地形图的相关计算1．计算两地间的相对高度从等高线图上读出任意两点的海拔，就可以计算这两点的相对高度：H相＝H高－H低。

2．计算两地间的气温差已知某地的气温和两地间的相对高度，根据对流层气温垂直递减率(0.6℃/100m)可计算两地间的气温差异：T差＝(0.6℃×H相)/100m。

3．估算陡崖的相对高度(1)陡崖的相对高度ΔH的取值范围是：(n—1)d≤ΔH<(n＋1)d。

(2)陡崖的绝对高度①陡崖崖顶的绝对高度：H大≤H顶<H大＋d。

②陡崖崖底的绝对高度：H小－d＜H底≤H小。

(注：n为陡崖处重合的等高线条数，d为等高距，H大为重合等高线中海拔最高的，H小为重合等高线中海拔最低的。

)4．估算某地形区的相对高度(1)估算方法：一般说来，若在等高线地形图上，任意两点之间有n条等高线，等高距为d，则这两点的相对高度H可用下面公式求算：(n—1)d＜H＜(n＋1)d。

(2)例证：如图所示，求A、B两点间的相对高度。

A、B两点之间有3条等高线，等高距为100m，利用公式可得A、B两点间的相对高度为200m＜H＜400m。

5．估算坡度(1)应用：一般情况下，如果坡度大于25°，则不宜修建梯田，因此，在山区能否修建梯田，常会用到坡度计算；此外山区道路修建也会对坡度进行估算。

(2)计算：公式tanα＝h/L。

(h为两点相对高度，可由两点等高线求出。

L为两点距离，可由图中比例尺与两点图上距离算出。

α为坡度，可由h/L的值再从数学用表中查出。

)【典型例题】(2012·新课标全国文综)下图示意某小区域地形，图中等高距为100米，瀑布的落差为72米。

据此完成下面两题。

1．Q地的海拔可能为( )A．90米B．230米C．340米D．420米2．桥梁附近河岸与山峰的高差最接近( )A．260米B．310米C．360米D．410米思维过程1．由图名、图例可知该图为等高线地形图，分布着山峰、河湖、瀑布、桥梁等。

等高线地形图中有关长度和面积的量算（原创）河北省邢台市邢台学院地理科学系陈霁冰风水规划研究室原创。

专业从事高考地理命题研究、风水规划设计、四柱命理预测邮编054001.邮箱：zhangbingtong@地理计算越来越注重和实际应用结合。

在等高线地形图中常见的计算有：河流长度、流域面积、库容、土石方等估算。

下面介绍几种简便易行的计算方法。

一、长度的量算长度的量算分两种：一种是直线长度的量算，一种是曲线长度的量算。

1.直线长度的量算用两脚规（或毫米刻度尺）最方便，先用两脚规或刻度尺量取图上两点间距离，然后结合本图的比例尺上，便可求出长度。

此法较简便。

2.曲线长度的量算在地图中出现的河流、海岸线、道路等多为曲线，考虑到考试中的实际需要，不需要太精确，可用下述两方法进行粗略估算。

①等长法：将曲线截成若干等长小线段（线段分得越小，精度越高），从一端开始进行连续测量（两脚规较方便），直到终点，最后如有距终点不足一个小线段长度，可估算该线段出长度。

然后用小线段的段数乘以小线段的长度再加上最后一个估算的线段长度，即为曲线图上长度。

最后结合图中比例尺就可求出曲线实际长度。

②不等长法：若曲线有较明显的数段不等长的线段构成，可用刻度尺直接量出各线段长度，然后相加，即为曲线的图上长度。

最后结合图中比例尺就可求出曲线实际长度。

二、面积量算在实际中经常会遇到地形图上面积的量算问题，如求算某河流流域面积、部分河段汇水面积、地形图中局部面积和土地利用类型面积等等。

比较简洁实用的是方格法。

方法：如图1所示，将所计算区域按一定的边长划分成多个小正方形，如边长一般取小于图示中比例尺单位长度的值（如0.5mm×0.5mm）较为合适且方便计算。

读出完整的方格数，然后再用目估方法将不完整的方格凑成完整的方格数。

最后累加出图形轮廓线内的总方格数。

用总方格数去乘每一方格代表的实地面积，即得欲测图形的总面积。

另外，方格画的越小，精度越高。

等高线计算公式等高线计算公式是地理学中常用的一种方法，用于表示地形的高度变化。

等高线是连接地球表面上具有相同高度的点的曲线，通过等高线可以直观地了解地形的起伏和山脉的分布。

下面将介绍等高线计算公式的基本原理和应用。

等高线计算公式的基本原理是根据地形的高度变化来确定等高线的间距和高度。

首先，需要确定一个基准点，通常选择海平面作为基准点。

然后，根据地形的高度变化，确定等高线的间距。

一般情况下，等高线的间距越小，表示地形的起伏越大。

最后，根据等高线的间距和高度，可以计算出每条等高线的具体高度。

等高线计算公式的应用非常广泛。

在地理学和地质学中，等高线可以用于绘制地形图和地质图，帮助人们了解地球表面的地形和地质特征。

在军事和航空领域，等高线可以用于制定作战计划和飞行路线，帮助军队和飞行员避开地形障碍。

在旅游和户外运动中，等高线可以用于规划徒步和登山路线，帮助人们安全地探索自然环境。

等高线计算公式的具体步骤如下：1. 确定基准点：选择一个基准点作为起点，通常选择海平面作为基准点。

2. 确定等高线间距：根据地形的高度变化，确定等高线的间距。

一般情况下，等高线的间距越小，表示地形的起伏越大。

等高线间距的选择需要根据具体情况进行，可以根据地图上的高度标志来确定。

3. 计算等高线高度：根据等高线的间距和高度，可以计算出每条等高线的具体高度。

计算公式为：等高线高度 = 基准点高度 + 等高线间距 ×等高线数量。

4. 绘制等高线图：根据计算得到的等高线高度，可以绘制出等高线图。

等高线图上的等高线越密集，表示地形的起伏越大。

需要注意的是，等高线计算公式只是一种近似方法，实际地形的高度变化可能会受到多种因素的影响，如地质构造、水文条件等。

因此，在使用等高线计算公式时，需要结合实际情况进行分析和判断。

总之，等高线计算公式是一种常用的地理学方法，可以帮助人们了解地形的高度变化。

通过计算等高线的间距和高度，可以绘制出等高线图，帮助人们更好地认识和利用地球表面的地形特征。

算等高线的公式算等高线的公式是地理学中常用的一种方法，用于表示地形图上的等高线。

等高线是连接地面上相同高度点的曲线，它反映了地形的高低起伏。

在地形图上，等高线的间距越窄，表示地形的起伏越大；等高线的间距越宽，表示地形的起伏越小。

等高线的公式可以用数学语言来描述，即通过数学函数来表示地形的高度。

一般而言，我们可以使用以下公式来计算等高线：h(x, y) = f(x, y)其中，h表示地形的高度，x和y表示地形上的任意点的坐标，f(x, y)表示地形上的高度函数。

高度函数f(x, y)可以是任意的数学函数，它决定了地形的形状和起伏。

常见的高度函数包括线性函数、二次函数、三次函数等。

在实际应用中，我们通常使用地理信息系统（GIS）来绘制地形图和计算等高线。

GIS软件可以根据地形数据和高度函数来自动生成等高线。

具体而言，GIS软件会根据地形数据中的高度信息，计算出地形上每个点的高度值，并根据等高线的间距设定，生成相应的等高线。

等高线的绘制可以采用等高线图的方式。

在等高线图中，等高线通过不同的线型、颜色或标签来表示不同的高度。

一般而言，等高线图的每条等高线都有一个对应的高度值，用于标识该等高线所代表的高度。

通过等高线图，我们可以直观地了解地形的高低起伏。

等高线图可以帮助我们判断地势的陡缓，识别山脉、河流、平原等地形特征，还可以用于规划工程建设、军事作战等领域。

除了等高线图，我们还可以使用等高线插值的方法来计算地形上任意点的高度值。

等高线插值是一种通过已知等高线数据来推测未知点高度的方法。

常见的等高线插值方法有三角网插值、反距离权重插值、克里金插值等。

这些插值方法可以根据已知点的高度值，推算出未知点的高度值，并用等高线的方式呈现出来。

算等高线的公式是地理学中重要的一种方法，它可以帮助我们了解地形的高低起伏，并在实际应用中发挥重要作用。

通过等高线图和等高线插值，我们可以更好地理解和利用地形信息，为各种领域的研究和应用提供支持。

例谈等高线地形图中的相关计算方法等高线（contour）是表示地形景观的重要工具，它能够将地形面分解成多个子区域，从而能够清楚地展示地形特征。

等高线地形图（contour map）是一种表示地形景观的重要图表，它可以帮助我们用一张图来直观地展示地形形势。

等高线地形图中的相关计算方法，是构建等高线地形图的重要工具，也是影响地形图展示精度的重要因素。

本文以例谈的形式，介绍等高线地形图中的常用计算方法。

1.地形景观简单统计在等高线地形图中，每个等高线都会连接组成地形景观的各个顶点（vertex），从而形成不同的地形景观。

地形景观的简单统计，就是将整个地形景观中的各个部分，依据其不同的组成部分进行统计。

比如，地形景观中有多少个等高线，有多少个组成等高线的顶点，以及各个等高线的长度等。

2.地形景观拓扑信息地形景观的拓扑信息，是指地形景观中相互关联的顶点，以及各个顶点之间的关系。

也就是说，地形景观的拓扑信息描述的是，地形景观中的各个等高线顶点以及等高线之间的关系。

比如，哪些顶点相邻，哪些顶点是等高线的尖锐点，哪些顶点是等高线的平滑点等。

3.等高线角度计算在等高线地形图中，每条等高线都有一定的方向和角度。

等高线角度计算，就是在地形景观中计算出每条等高线的方向和角度，以此来精确表示地形景观的方向和角度。

4.等高线曲率计算等高线曲率计算，是指在等高线地形图中，计算每条等高线的曲率，以此来描述地形景观的曲率。

曲率的计算方法有很多种，主要是基于二次曲率、后验求解、边长比变换等方法。

5.地形要素分析地形要素分析，是指从等高线地形图中，提取出地形要素，以此帮助地形学者更容易识别地形要素。

比如，可以提取出平坡、坡脊、山谷、峰顶等地形要素。

6.地形距离计算地形距离计算，是指从等高线地形图中，计算出不同顶点之间的距离，从而用来表示地形的距离关系。

比如，从点A到点B的距离，从点A到点C的距离等。

以上便是等高线地形图中的常用计算方法。

算等高线的公式算等高线的公式是指在数学中用来表示地形等高线的数学公式。

等高线是指连接相同高度的点所形成的线。

在地理学中，等高线用来表示地形的高度和形态。

等高线的公式可以用数学语言来表示，一般使用二维平面上的函数方程来描述。

常用的等高线公式有以下几种形式：1. 等高线方程：z = f(x, y)这是最常见的等高线公式，其中z表示高度，f(x, y)表示地形表面上的点的高度函数。

在二维平面上，可以通过将x和y代入函数来确定地形表面上的点的高度，从而得到等高线。

2. 等高线方程：ax + by + c = 0这是一种较简单的等高线公式，其中a、b和c是常数。

通过将x和y代入方程，可以得到满足等高线条件的点。

3. 等高线方程：r = a + bθ这是一种极坐标下的等高线公式，其中r表示距离原点的距离，θ表示与x轴的夹角，a和b是常数。

通过改变θ的值，可以得到不同高度上的等高线。

4. 等高线方程：z = ax^2 + by^2 + c这是一个二次函数的等高线公式，其中a、b和c是常数。

通过将x和y代入方程，可以得到满足等高线条件的点。

通过使用这些等高线公式，可以在地图上绘制出地形的等高线图。

等高线图可以帮助我们更好地理解地形的高度和形态，从而在农业、城市规划、地质勘探等领域提供重要的参考信息。

除了使用等高线公式来描述地形的高度和形态，还可以利用地形数据来生成等高线。

现代技术可以通过卫星遥感、激光雷达等手段获取大量的地形数据，然后利用计算机算法来生成等高线图。

这种方法可以更精确地绘制地形的等高线图，提供更准确的地形信息。

等高线的公式是描述地形等高线的数学公式。

通过使用这些公式，可以在地图上绘制出地形的等高线图，帮助我们更好地理解地形的高度和形态。

现代技术可以利用地形数据来生成等高线图，提供更准确的地形信息。

等高线图在农业、城市规划、地质勘探等领域具有重要的应用价值。