欢迎光临指导
一、问题的引入
我们知道,物体作匀速直线运动的位 移S是时间t的函数,即s=vt,其中v是常量。 在实际问题中常常需要求时间t,即 t=s/v,这时,时间t是位移s的函数.我们 把t=s/v叫s=vt的反函数。 这一节课我们就来研究反函数。
问题1:函数s=vt的定义域,值域分别是 什么? 问题2:函数t=s/v中谁是谁的函数? 问题3:函数s=vt与函数t=s/v之间有什么 关系
(4)
2x 3 y ( x R x 1 , 且 ) x 1
x3 y ( x R x 2 , 且 ) x2
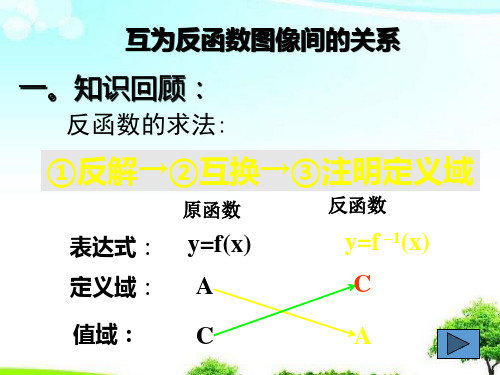
八、求函数反函数的步骤:
1 求原函数的值域。
2 由y=f(x)反解出x = f 1(y)。
3 把 x = f 1(y)中 x与y互换得y = f 1(x).
三、反函数定义:
函数y=f(x)(x∈A) 中,设它的值域为 C。 我们根据这个函数中x,y的关系, 用 y 把 x 表示出来,得到 x = (y) 。
如果对于y在C中的任何一个值,通过x = (y) ,x在A中都有唯一的值和它对应,
那么, x = (y)就表示y是自变量,x是自变量 y 的函数。这样的函数 x = (y)(y ∈C)叫做 函数y=f(x)(x∈A)的反函数.
二.问题的研究
函数y=2x+6的定义域为:A=R, 值域C=R,建立了如下的映射 。 问题:能否建立C到A的对应,让y 与x对应?这个新的对应是函数吗? A x x=?
f
?
C y 2x 6 y
函数 y 2 x 6( x R)中,x是自变量,
y是x的函数, 从函数 y 2 x 6 中解出x, y 得到 x 3( y R) 2 这样,对于y在R中任何一个值,通过式子 y x 3, x在R中都有唯一的值和它对应。 2 这时 y 为自变量,x 作为 y 的函数 这样的函数称为原函数的反函数 怎么给反函数下定义呢?