苏科版九年级下6.6图形的位似同步练习及答案

图形的位似--巩固练习一、选择题1.下面给出了相似的一些命题：（1）菱形都相似；（2）等腰直角三角形都相似；（3）正方形都相似；（4）矩形都相似；（5）正六边形都相似.其中正确的有（）A．2个 B．3个 C．4个 D．5个2.下列说法错误的是（）A.位似图形一定是相似图形.B.相似图形不一定是位似图形.C.位似图形上任意一对对应点到位似中心的距离之比等于相似比.D.位似图形中每组对应点所在的直线必相互平行.3.下列说法正确的是（）A.分别在ABC的边AB、AC的反向延长线上取点D、E，使DE∥BC，则ADE是ABC放大后的图形.B.两位似图形的面积之比等于相似比.C.位似多边形中对应对角线之比等于相似比.D.位似图形的周长之比等于相似比的平方.4．如图，在平面直角坐标系中，已知点A（﹣3，6），B（﹣9，﹣3），1，把△ABO缩小，则点A的对应点以原点O为位似中心，相似比为3A '的坐标是 （ ）A ．（﹣1，2）B ．（﹣9，18）C ．（﹣9，18）或（9，﹣18）D ．（﹣1，2）或（1，﹣2）第4题 第7题5.下列命题：①两个正方形是位似图形；②两个等边三角形是位似图形；③两个同心圆是位似图形；④平行于三角形一边的直线截这个三角形的两边，所得的三角形与原三角形是位似图形.其中正确的有( )A.1个B.2个C.3个D.4个6．如果点C 为线段AB 的黄金分割点，且AC ＞BC ，则下列各式不正确的是 （ ）7.已知矩形ABCD 中，AB=1，在BC 上取一点E ，沿AE 将△ABE 向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，则AD= （）二、填空题8. 如果两个位似图形的对应线段长分别为3cm和5cm，且较小图形周长为30cm，则较大图形周长为__________.9.如图，在平面直角坐标系中，已知A（1，0），D（3，0），△ABC与△DEF位似，原点O是位似中心．若AB=1.5，则DE= ．第9题第10题10．如图，以点O为位似中心，将五边形ABCDE放大后得到五边形，已知OA=10cm，OA′=20cm，则五边形ABCDE的周长与五边形的周长的比值是__________．11. △ABC中，D、E分别在AB、AC上，DE∥BC，△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分，则AD：AB=________.A B C D E'''''A B C D E'''''12. 把一矩形纸片对折，如果对折后的矩形与原矩形相似，则原矩形纸片的长与宽之比为___________.13.如图，以O为位似中心，将边长为256的正方形OABC依次作位似1，变换，经第一次变化后得正方形OA1B1C1，其边长OA1缩小为OA的21，经第，经第二次变化后得正方形OA2B2C2，其边长OA2缩小为OA1的21，…，依次规三次变化后得正方形OA3B3C3，其边长OA3缩小为OA2的2律，经第n次变化后，所得正方形OA n B n C n的边长为正方形OABC边长的倒数，则n= ．第13题第14题14. 如图，△ABC中，AB=AC=4，∠BAC=36°，∠ABC的平分线与AC 边的交点D为边AC的黄金分割点（AD＞DC），则BC=___________.三、综合题15.如图，D、E分别AB、AC上的点.(1)如果DE∥BC，那么△ADE和△ABC是位似图形吗？为什么？(2)如果△ADE和△ABC是位似图形，那么DE∥BC吗？为什么？16.如图，F在BD上，BC、AD相交于点E，且AB∥CD∥EF，（1）图中有哪几对位似三角形，选其中一对加以证明；（2）若AB=2，CD=3，求EF的长．17. 如图1，矩形ODEF的一边落在矩形ABCO的一边上，并且矩形ODEF（1）求矩形ODEF的面积；（2）将图1中的矩形ODEF绕点O逆时针旋转一周，连接EC、EA，△ACE的面积是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，请说明理由．一、选择题1．【答案】B【解析】（1）菱形的角不一定对应相等，故错误； （2）（3）（5）符合相似的定义，故正确； （4）对应边的比不一定相等．故错误． 故正确的是：（2）（3）（5）．故选B ． 2．【答案】D. 3．【答案】C. 4.【答案】D.【解析】∵A （﹣3，6），B （﹣9，﹣3），以原点O 为位似中心，相似比为，把△ABO 缩小，∴点A 的对应点A ′的坐标为（316313⨯⨯-，）或[)31(6)31(3-⨯-⨯-，]，即A ′点的坐标为（﹣1，2）或（1，﹣2）． 5．【答案】B【解析】由位似图形的概念可知③和④对，故选B. 6．【答案】D.【解析】∵ AC ＞BC ，∴ AC 是较长的线段，,AB ACAC ≈0.618AB ．故选D ．7.【答案】B. 【解析】∵ AB=1，设AD=x ，则FD=x -1，FE=1， ∵ 四边形EFDC 与矩形ABCD 相似，二、填空题 8.【答案】50cm. 9.【答案】4.5．【解析】∵ △ABC 与DEF 是位似图形，它们的位似中心恰好为原点，已知A 点坐标为（1，0），D 点坐标为（3，0）， ∴ AO=2，DO=5，∴==，∵ AB=1.5，∴ DE=4.5． 故答案为：4.5．11x =-10.【答案】1：2．【解析】∵ 五边形ABCDE 与五边形A ′B ′C ′D ′E ′位似，OA=10cm ，OA ′=20cm ，∴ 五边形ABCDE ∽五边形A ′B ′C ′D ′E ′，且相似比为：OA ：OA ′=10：20=1：2，∴ 五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比为：OA ：OA ′=1：2． 故答案为：1：2． 11.【答案】2:2 .【解析】由BC ∥DE 可得△ADE ∽△ABC ，所以，故.【解析】矩形ABCD 对折后所得矩形与原矩形相似，则矩形ABCD ∽ 矩形BFEA ，设矩形的长为a ，宽为b ．则AB=CD=b ，AD=BC=a ，BF=AE=13. 【答案】16.【解析】由图形的变化规律可得：2561256)21(=⨯n ， 解得n =16． 14. 【解析】∵ AB=AC ，∠A=36°，∴ ∠ABC=∠C=72°， 又BD 平分∠ABC ，∴ ∠ABD=∠CBD=36°，∴ ∠BDC=72°，∴ BC=BD=AD ， 三、解答题 15.【答案与解析】(1)△ADE 和 △ABC 是位似图形.理由是：DE∥BC，所以∠ADE=∠B，∠AED=∠C.所以△ADE∽△ABC，所以.又因为点A是△ADE和△ABC的公共点，点D和点B是对应点，点E和点C是对应点，直线BD与CE交于点A，所以△ADE和△ABC是位似图形.(2)DE∥BC.理由是：因为△ADE和△ABC是位似图形，所以△ADE∽△ABC 所以∠ADE=∠B 所以DE∥BC.16.【答案与解析】解：（1）△DFE与△DBA，△BFE与△BDC，△AEB与△DEC都是位似图形，理由：∵ AB∥CD∥EF，∴△DFE∽△DBA，△BFE∽△BDC，△AEB∽△DEC，且对应边都交于一点，∴△DFE与△DBA，△BFE与△BDC，△AEB与△DEC都是位似图形；（2）∵△BFE∽△BDC，△AEB∽△DEC，AB=2，CD=3，∴==，∴==，解得：EF=．17.【答案与解析】（1）∵矩形ODEF∽矩形ABCO，其相似比为1：4，（2）存在．所以点E的轨迹为以点O为圆心，以2为半径的圆，设点O到AC的距离为h，.。

HM GFNCBA ED 九年级数学下册同步练习6.6图形的位似一、选择题1.若两个图形位似，则下列叙述不正确的是（）A．两个图形的面积比等于位似比的平方B．两个图形上的对应线段必平行C．两个图形上的对应线段之比等于位似比D．每对对应点所在直线交于同一点2.下列关于位似图形的表述：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于相似比.A.②③B.①②C.③④D.②③④3.如图，正五边形FGHMN是由正五边形ABCDE经过位似变换得到的，若AB∶FG＝2∶3，则下列结论正确的是（）A．2DE＝3MN B．3DE＝2MN C．3∠A＝2∠F D．2∠A＝3∠F 4.如图，点P（8，6）在△ABC的边AC上，以原点O为位似中心，在第一象限内将△ABC缩小到原来的，得到△A′B′C′，点P在A′C′上的对应点P′的的坐标为（）A．（4，3） B．（3，4）C．（5，3）D．（4，4）第3题第4题第5题5.如图，BC∥DE，下列说法不正确的是（）A．两个三角形是位似图形B．点A是两个三角形的位似中心C．B与D，C与E是对应位似点D．AE：AD是相似比6.在平面直角坐标系中，点P（1，﹣2）是线段AB上一点，以原点O为位似中心把△AOB放大到原来的两倍，则点P对应点的坐标为（）A．（2，﹣4）B．（2，﹣4）或（﹣2，4）C．（，﹣1）D．（，﹣1）或（﹣，1）7.已知下列四种变化：①向下平移2个单位长度；②向左平移2个单位长度；③横坐标变为原来的2倍，纵坐标不变；④纵坐标变为原来的2倍，横坐标不变．若将函数y＝x2+1图象上的所有点都经过三次变化得到函数y＝x2+x的图象，则这三次变化的顺序可以是（）A．③→④→①B．③→①→②C．④→②→①D．①→④→②8.如图，△DEF和△ABC是位似图形点O是位似中心，点D，E，F，分别是OA，OB，OC的中点，若△ABC的面积是8，△DEF的面积是（）A．2B．4C．6D．8二、填空题9.如果两个位似图形的对应线段长分别为3cm和5cm，且较小图形的周长为36cm，则较大图形的周长为＿＿＿＿＿＿.10.如果把直角坐标系内多边形各点的横坐标与纵坐标均乘以2，则所得多边形与原多边形是＿＿＿＿＿＿，它们的面积之比为＿＿＿＿＿＿。

图形的位似A组题1、利用位似形只能将一个图形放大，这句话_______（填“正确”或“不正确”）。

2、两个构成位似的三角形其相似比为k，则对应点到位似中心的距离之比为__ ___。

3、下列说法中：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形若全等，则位似中心在两个图形之间；④若五边形ABCDE与五边形A＇B＇C＇D＇E＇位似，则其中△ABC与△A＇B＇C＇也是位似的，且相似比相等。

其中正确的个数有（）A、1个B、2个C、3个D、4个4、若两个图形位似，则下列叙述不正确的是（）A、每对对应点所在的直线相交于同一点B、两个图形上对应线段之比等于位似比C、两个图形上对应线段必平行D、两个图形的面积比等于位似比的平方5、下列说法正确的是（）A、分别在△ABC的边AB、AC的反向延长线上取点D、E，使DE∥BC，则△ADE是△ABC放大后的图形；B、两位似图形的面积比等于位似比；C、位似多边形中对应对角线之比等于位似比；D、位似图形的周长之比等于位似比的平方。

6、某习小组在讨论“变化的鱼”时，知道大鱼和小鱼是位似图形（如上图所示），则小鱼上的点（a，b）对应大鱼上的点（）A、（-2a，-2b）B、（-a，-2b）C、（-2b，-2a）D、（-2a，-b）7、按如下方法将△ABC的三边缩小来原来的12。

任取一点O，连AO，•BO，CO，并取它们的中点D，E，F，得△DEF，则下列说法中正确的个数是（）①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形③△ABC与△DEF是周长的比为2：1④△ABC与△DEF面积比为4：1A、1个B、2个C、3个D、4个8、已知，如图，E（-4，2），F（-1，-1），以点O为位似中心，按比例尺1：2，把△EFO缩小，•则点E的对应点E′的坐标为（）A、（2，-1）或（-2，1）B、（8，-4）或（-8，4）y EC 、（2，-1）D 、（8，-4）9、如图△ABC 。

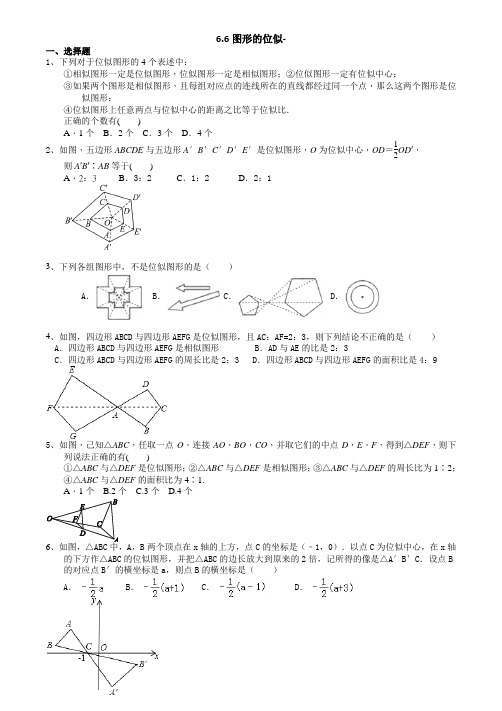
6.6图形的位似-一、选择题1、下列对于位似图形的4个表述中：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比． 正确的个数有( )A ．1个B ．2个C ．3个D ．4个2、如图，五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形，O 为位似中心，OD ＝12OD ′，则A ′B ′∶AB 等于( )A ．2：3B ．3：2C ．1：2D ．2：13、下列各组图形中，不是位似图形的是（ ）A ．B ．C ．D ．4、如图，四边形ABCD 与四边形AEFG 是位似图形，且AC ：AF=2：3，则下列结论不正确的是（ ） A ．四边形ABCD 与四边形AEFG 是相似图形 B ．AD 与AE 的比是2：3C ．四边形ABCD 与四边形AEFG 的周长比是2：3 D ．四边形ABCD 与四边形AEFG 的面积比是4：95、如图，己知△ABC ，任取一点O ，连接AO ，BO ，CO ，并取它们的中点D ，E ，F ，得到△DEF ，则下列说法正确的有( )①△ABC 与△DEF 是位似图形；②△ABC 与△DEF 是相似图形；③△ABC 与△DEF 的周长比为1∶2；④△ABC 与△DEF 的面积比为4∶1. A ．1个 B .2个 C .3个 D .4个A ，B 两个顶点在x 轴的上方，点C 的坐标是（﹣1，0）．以点C 为位似中心，在x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的2倍，记所得的像是△A ′B ′C ．设点B 的对应点B ′的横坐标是a ，则点B 的横坐标是（ ）A ．B ．C ．D ．7、如图，已知点E （﹣4，2)，点F （﹣1，﹣1），以O 为位似中心，把△EFO 放大为原来的2倍，则E 点的对应点坐标为（ ） A ．（2,﹣1）或（﹣2，1） B ．（8，-4）或（﹣8，4） C ．（2，﹣1） D ．（8，﹣4）8、如图所示，正方形OEFG 和正方形ABCD 是位似图形，点F 的坐标为(－1，1)，点C 的坐标为(－4，2)，则这两个正方形位似中心的坐标是________．A.(2，0)B.(－43，23)C.(2,2)D.(2，0)或(－43，23)二、填空题9、如图，△ABO 三个顶点的坐标分别为A (2，4)，B (6，0)，O (0，0)．以原点O 为位似中心，把这个三角形缩小为原来的12，可以得到△A ′B ′O ，已知点B ′的坐标是(3，0)，则点A ′的坐标是________．10、如图所示，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2.若AB ＝2 cm ，则A ′B ′＝_______cm ，在图中画出位似中心O .11111是以点O 为位似中心的位似三角形，若C 1为OC 的中点，AB ＝4，1B 1的长为________.12ABCDE 放大后得到五边形A ′B ′C ′D ′E ′，已知OA=10cm ，OA ′=20cm ，则五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是______．13、如图，A′B′∥AB ，B′C′∥BC ，且OA′∶A′A ＝4∶3，则△ABC 与___________是位似图形，相似比是_________．14、如图，△ABC与△DEF位似，位似中心为点O，且BC：EF＝3：2，则S△ABC：S△DEF＝．15、如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD＝90°，CO＝CD，若B（1，0），则点C的坐标为．16、如图，O点是△ABC与△D1E1F1的位似中心，△ABC的周长为1.若D1、E1、F1分别是线段OA、OB、OC的中点，则△D1E1F1的周长为12；若OD2＝13OA、OE2＝13OB、OF2＝13OC，则△D2E2F2的周长为13；…若ODn＝13OA、OEn＝13OB、OFn＝13OC，则△DnEnFn的周长为_____．(用正整数n表示)三、解答题17、如图，在网格图中，每格是边长为1的正方形，四边形ABCD的顶点均为格点．（1）请以点O为位似中心，在网格中作出四边形A'B'C'D'，使四边形A'B'C'D'与四边形ABCD位似，且＝2；（2）线段C'D'的长为；（3）求出△A'B'O的面积．18、如图，在矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BC于E点，连接DE交OC于F点，作FG⊥BC于G点，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．19、如图，△ABC 三个顶点的坐标分别为A (－1，3)，B (－1，1)，C (－3，2)．(1)请画出△ABC 关于y 轴对称的△A 1B 1C 1； (2)以原点O 为位似中心，将△A 1B 1C 1放大为原来的2倍，得到△A 2B 2C 2，请在第三象限内画出△A 2B 2C 2，并求出S △A △A 2B 2C 2的值．20、如图，方格纸中每个小正方形的边长为1，ABC 和DEF 的顶点都在方格纸的格点上．（1）判断ABC 和DEF 是否相似，并说明理由；（2）以点E 为中心，在位似中心的同侧画出EDF 的一个位似11ED F ，使得它与EDF 的相似比为2:1； （3）求ABC 与11ED F 的面积比．6.6图形的位似-苏科版九年级数学下册 巩固训练（答案）一、选择题1、下列对于位似图形的4个表述中：①相似图形一定是位似图形，位似图形一定是相似图形；②位似图形一定有位似中心；③如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形；④位似图形上任意两点与位似中心的距离之比等于位似比． 正确的个数有( )A ．1个B ．2个C ．3个D ．4个[解析] 相似图形不一定是位似图形，位似图形一定是相似图形，①错误；位似图形一定有位似中心，②正确；如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么这两个图形是位似图形，③正确；位似图形上对应两点与位似中心的距离之比等于位似比，④错误．故选B .2、如图，五边形ABCDE 与五边形A ′B ′C ′D ′E ′是位似图形，O 为位似中心，OD ＝12OD ′，则A ′B ′∶AB 等于( )A ．2：3B ．3：2C ．1：2D ．2：1[解析] 因为OD ＝12OD′，所以OD OD′＝12，所以五边形ABCDE 与五边形A′B′C′D′E′的位似比为12，所以AB A′B′＝12，所以A′B′∶AB ＝2∶1.故选 D3、下列各组图形中，不是位似图形的是（ B ）A ．B ．C ．D ．4、如图，四边形ABCD 与四边形AEFG 是位似图形，且AC ：AF=2：3，则下列结论不正确的是（ B ） A ．四边形ABCD 与四边形AEFG 是相似图形B ．AD 与AE 的比是2：3C ．四边形ABCD 与四边形AEFG 的周长比是2：3 D ．四边形ABCD 与四边形AEFG 的面积比是4：95、如图，己知△ABC ，任取一点O ，连接AO ，BO ，CO ，并取它们的中点D ，E ，F ，得到△DEF ，则下列说法正确的有( )①△ABC 与△DEF 是位似图形；②△ABC 与△DEF 是相似图形；③△ABC 与△DEF 的周长比为1∶2；④△ABC 与△DEF 的面积比为4∶1. A ．1个 B .2个 C .3个 D .4个ABC 与△DEF 是位似图形，故①正确； △ABC 与△DEF 是相似图形，故②正确；∵将△ABC 的三边缩小为原来的一半得到△DEF ，∴△ABC 与△DEF 的周长比为2∶1，故③错误；根据面积比等于相似比的平方，得△ABC 与△DEF 的面积比为4∶1，故④正确．故选C.6、如图，△ABC 中，A ，B 两个顶点在x 轴的上方，点C 的坐标是（﹣1，0）．以点C 为位似中心，在x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的2倍，记所得的像是△A ′B ′C ．设点B 的对应点B ′的横坐标是a ，则点B 的横坐标是（ D ）A ．B ．C ．D ．7、如图，已知点E （﹣4，2)，点F （﹣1，﹣1），以O 为位似中心，把△EFO 放大为原来的2倍，则E 点的对应点坐标为（ B ） A ．（2,﹣1）或（﹣2，1） B ．（8，-4）或（﹣8，4） C ．（2，﹣1） D ．（8，﹣4）8、如图所示，正方形OEFG 和正方形ABCD 是位似图形，点F 的坐标为(－1，1)，点C 的坐标为(－4，2)，则这两个正方形位似中心的坐标是________．A.(2，0)B.(－43，23)C.(2,2)D.(2，0)或(－43，23)[①当两个位似图形在位似中心O ′同旁时，位似中心就是直线CF 与x 轴的交点．设直线CF 的函数表达式为y ＝kx ＋b (k ≠0)，将C (－4，2)，F (－1，1)的坐标代入，得⎩⎨⎧－4k ＋b ＝2，－k ＋b ＝1，解得⎩⎨⎧k ＝－13，b ＝23，即y ＝－13x ＋23.令y ＝0，得x ＝2，∴点O ′的坐标是(2，0)． ②当位似中心O ′在两个正方形之间时，可求直线OC 的函数表达式为y ＝－12x ，直线DE 的函数表达式为y ＝14x ＋1，由⎩⎨⎧y ＝－12x ，y ＝14x ＋1， 解得⎩⎨⎧x ＝－43，y ＝23，即O ′(－43，23)．故答案为(2，0)或(－43，23)．二、填空题9、如图，△ABO 三个顶点的坐标分别为A (2，4)，B (6，0)，O (0，0)．以原点O 为位似中心，把这个三角形缩小为原来的12，可以得到△A ′B ′O ，已知点B ′的坐标是(3，0)，则点A ′的坐标是________．[解析] ∵点A 的坐标为(2，4)，以原点O 为位似中心，把这个三角形缩小为原来的12，∴点A ′的坐标是(2×12，4×12)，即(1，2)．故答案为(1，2)．10、如图所示，△ABC 与△A ′B ′C ′是位似图形，且位似比是1∶2.若AB ＝2 cm ，则A ′B ′＝__4______cm ，在图中画出位似中心O .A 1B 1C 1是以点O 为位似中心的位似三角形，若C 1为OC 的中点，AB ＝4，则A 1B 1的长为________.[解析] ∵△ABC 和△A 1B 1C 1是以点O 为位似中心的位似三角形，C 1为OC 的中点，AB ＝4，∴A 1B 1＝12AB ＝2.12、如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形A ′B ′C ′D ′E ′，已知OA=10cm ，OA ′=20cm ，则五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比值是__1：2____．13、如图，A′B′∥AB ，B′C′∥BC ，且OA′∶A′A ＝4∶3，则△ABC 与___________是位似图形，相似比是_________．答案:△A′B′C′；7∶414、如图，△ABC 与△DEF 位似，位似中心为点O ，且BC ：EF ＝3：2，则S △ABC ：S △DEF ＝ ．解：∵△ABC 与△DEF 位似，∴△ABC ∽△DEF ， ∵BC ：EF ＝3：2，∴＝（）2＝，故答案为：9：4．15、如图，△OAB 与△OCD 是以点O 为位似中心的位似图形，相似比为1：2，∠OCD ＝90°，CO ＝CD ，若B （1，0），则点C 的坐标为 ．解：∵∠OAB ＝∠OCD ＝90°，AO ＝AB ，CO ＝CD ，等腰Rt △OAB 与等腰Rt △OCD 是位似图形，点B 的坐标为（1，0），∴BO ＝1，则AO ＝AB ＝， ∴A （，），∵等腰Rt △OAB 与等腰Rt △OCD 是位似图形，O 为位似中心，相似比为1：2， ∴点C 的坐标为：（1，1）． 故答案为：（1，1）．16、如图，O 点是△ABC 与△D 1E 1F 1的位似中心，△ABC 的周长为1.若D 1、E 1、F 1分别是线段OA 、OB 、OC 的中点，则△D 1E 1F 1的周长为12；若OD 2＝13OA 、OE 2＝13OB 、OF 2＝13OC ，则△D 2E 2F 2的周长为13；…若ODn ＝13OA 、OEn ＝13OB 、OFn ＝13OC ，则△DnEnFn 的周长为___1n __．(用正整数n 表示)三、解答题17、如图，在网格图中，每格是边长为1的正方形，四边形ABCD的顶点均为格点．（1）请以点O为位似中心，在网格中作出四边形A'B'C'D'，使四边形A'B'C'D'与四边形ABCD位似，且＝2；（2）线段C'D'的长为；（3）求出△A'B'O的面积．解：（1）如图所示，四边形A'B'C'D'即为所求；（2）线段C'D'的长为＝，故答案为：；（3）△A'B'O的面积为×4×2+×4×2＝4+4＝8．18、如图，在矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BC于E点，连接DE交OC于F点，作FG⊥BC于G点，则△ABC与△FGC是位似图形吗？若是，请说出位似中心，并求出相似比；若不是，请说明理由．解:△ABC与△FGC是位似图形，位似中心是点C.因为在矩形ABCD中，AD∥B C，所以∠FAD＝∠FCE，∠FDA＝∠FEC，所以△AFD∽△CFE，所以CF CE AF AD=因为AD＝BC，所以CF CE AF CB=因为∠ABC＝90°，OE⊥BC，所以OE∥AB.因为OA＝OC，所以CE＝12BC，所以CFAF＝12,所以CFAC＝13.即△ABC与△FGC的相似比为3∶1.19、如图，△ABC三个顶点的坐标分别为A(－1，3)，B(－1，1)，C(－3，2)．(1)请画出△ABC关于y轴对称的△A1B1C1；(2)以原点O为位似中心，将△A1B1C1放大为原来的2倍，得到△A2B2C2，请在第三象限内画出△A2B2C2，并求出S△A1B1C1S△A2B2C2的值．解：(1)如图所示，△A1B1C1即为所求．(2)如图所示，△A2B2C2即为所求．∵将△A1B1C1放大为原来的2倍得到△A2B2C2，∴△A1B1C1∽△A2B2C2，且位似比为12，∴S△A1B1C1∶S△A2B2C2＝(12)2＝14.20、如图，方格纸中每个小正方形的边长为1，ABC和DEF的顶点都在方格纸的格点上．（1）判断ABC和DEF是否相似，并说明理由；（2）以点E为中心，在位似中心的同侧画出EDF的一个位似11ED F，使得它与EDF的相似比为2:1；（3）求ABC与11ED F的面积比．解:()1AB25AC5BC5EF10FD2ED22，，，，，======，∴BC10AC510AB2510EF FD ED10222======，，，∴BC AC ABEF FD ED==，∴ABC DEF∽；（2）延长ED到点1D，使12ED ED=，延长EF到点1F，使12EF EF=，连结11D F，则11ED F 为所求，如图；()113ABC DEF DEF D EF∽，∽，∴11ABC D EF∽，∴11ABC ED F与的面积比2211AC55()(D F822===．6.7 《用相似三角形解决问题》（满分120分；时间：120分钟）真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！题号一二三总分得分一、选择题（本题共计9小题，每题3 分，共计27分，）1. 如图，在中，．C.①②③D.①②③④ A.①② B.③④2 某同学想利用影长测量学校旗杆的高度，如图，他在某一时刻立米长的标杆测得其影厂为米，同时旗杆的投影一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为米和米，则学校旗杆的高度为（）米．A. B. C. D.3 如图，在中，＝，＝，点是的中点，连接，过点作，分别交，于点，，与过点且垂直于的直线相交于点，连接，给出以下五个结论：①；②＝；③点是的中点；④；⑤＝，其中正确结论有（）个．A. B. C. D.4. 如图，是一个照相机成像的示意图，如果底片宽，焦距是，所拍摄的外的景物的宽为( )A. B. C. D.5. 如图，在矩形中，点是的中点，的平分线交于点，将沿折叠，点恰好落在上点处，延长，交于点．有下列四个结论：①垂直平分；②平分；③；④．其中，将正确结论的序号全部选对的是（）A.①②③B.①②④C.②③④D.①②③④6. 如图，在正方形中，为正方形内一点，且，，将绕点逆时针旋转得到，连接、、，为的中点，连接．有下列结论：①为等腰直角三角形；②；③；④．其中正确结论的个数是（）A. B. C. D.7. 如图所示：两根竖直的电线杆长为，长为，交于于点点，则到地面的距离的长是（）A. B. C. D.8. 如图，为等边三角形，，，连接，为的中点，连接并倍长，连接、、．下列结论：①；②若，则；③在②的条件下，若，则．其中正确的有（）A.①②③都正确B.只有①②正确C.只有②③正确D.只有①③正确9 四边形为直角梯形，，为边上的中点，连接交于点，过点作于，的延长线交于点，则：①；②为的中点；③，则正确的结论有（）A.只有①②B.只有①③C.只有②③D.①②③二、填空题（本题共计7 小题，每题3 分，共计21分，）10. 有一支夹子如图所示，，，在夹子前面有一个长方体硬物，厚为，如果想用夹子的尖端、两点夹住、两点，那么手握的地方至少要张开________ ．11. 王宏身高米，为了测出路灯的高度，他从路灯出发沿平直道路以米/秒的速度向东匀速走开，某时他的影子长米，再过秒，他的影子长为米，则路灯高度为________米．12. 如图，测量小玻璃管管径的量具，的长为，被分为等份．如果玻璃管的管径正好对着量具上等份处，那么小玻璃管的管径________．13. 如图，在离某建筑物米处有一棵树，在某时刻，将长的竹竿竖直立在地面上，影长为，此时，树的影子照射到地面，还有一部分影子投影在建筑物的墙上，墙上的影子长为，那么这棵树高约为________米．14. 在同一时刻，米高的竹竿影长为米，那么影长为米的楼的高度为________米．15 如图，在等边中，于，点在的延长线上，点在上，，的延长线交的延长线于．若，，则________．三、解答题（本题共计7 小题，共计75分，）16 有一块三角形纸板（如图），，，小华想用它剪一个正方形，使正方形的每个顶点都在三角形的边上，请你帮她计算剪下的正方形的边长．17. 两棵树的高度分别是米，米，两棵树的根部之间的距离米．小强沿着正对这两棵树的方向从右向左前进，如果小强的眼睛与地面的距离为米，当小强与树的距离等于多少时，小强的眼睛与树、的顶部、恰好在同一条直线上，请说明理由．18. 如图，在梯形中，，，，，动点从点出发沿方向以的速度向点运动，动点同时以相同速度从点出发沿方向向终点运动，其中一个动点到达端点时，另一个动点也随之停止运动．（1）求的长：（2）当的面积为时，求运动时间；（3）当运动时间为何值时，的面积达到最大，并求出的最大值．19. 如图，小明和大伟想利用所学的几何知识测量学校操场上旗杆的高度，他们的测量方案如下：他们两次利用镜子，第一次他把镜子放在点，人在点正好在镜子中看见旗杆顶端：第二次把镜子放在点，人在点正好在镜子中看到旗杆顶端；已知图中的所有点均在同一平面内，，，，小明的眼晴距离地面的距离＝＝米，量得＝米，＝米，＝米，请你利用这些数据求出旗杆的高度．20. 如图，在中，，，，动点从点开始沿边向点以每秒个单位长度的速度运动，动点从点沿边向点以每秒个单位长度的速度运动，过点作，交于点，连接．点，分别从、同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为秒．（1）当为何值时，的面积为？（2）当为何值时，以点、、为顶点的三角形与相似？（3）是否存在这样的，使为等腰三角形？若存在，求出的值；若不存在，请说明理由．21. 如图，在中，，．（1）求的度数；（2）如图，延长到，使，延长到，使，、交于点．求证：；（3）如图，点、分别是、上的动点，且，作，，分别交于点、，线段、、能否始终组成直角三角形？给出你的结论，并说明理由．22. 如图，四边形是矩形，点是对角线上一动点（不与、重合），连接，过点作，交射线于点，已知，．设的长为．（1）________；当时，________；（2）①试探究：否是定值？若是，请求出这个值；若不是，请说明理由；②连接，设的面积为，求的最小值．（3）当是等腰三角形时．请求出的值；。

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！课时练6.6图形的位似一、选择题1.如图1,四边形ABCD与四边形GBEF是位似图形,则位似中心是()图1A.点AB.点BC.点FD.点D2.下列关于位似图形的四种表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确的有()A.1个B.2个C.3个D.4个3.如图2,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA∶OA1=1∶3,则五边形ABCDE和五边形A1B1C1D1E1的面积比是()图2A.1∶2B.1∶3C.1∶4D.1∶94在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A.四边形NPMQB.四边形NPMRC.四边形NHMQD.四边形NHMR5.已知△ABC与△A1B1C1是以原点为位似中心的位似图形,且A(3,1),△ABC与△A1B1C1的相似比为12,则点A的对应点A1的坐标是()A.(6,2)B.(-6,-2)C.(6,2)或(-6,-2)D.(2,6)二填空题6.如图3,四边形ABCD与四边形A'B'C'D'位似,位似中心为点O,OC=6,CC'=4,AB=3,则A'B'=.7.如图在平面直角坐标系中,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为2∶3,点B,E在第一象限.若点A的坐标为(4,0),则点E的坐标是.8.在平面直角坐标系中,点A的坐标是(-2,1),以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为A'.若点A'恰在某一反比例函数的图像上,则该反比例函数的表达式为.9.如图9,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为13,点A,B,E在x轴上.若正方形BEFG的边长为6,则点C的坐标为.图910.如图10,已知▱ABCD,以点B为位似中心,作▱ABCD的位似图形▱EBFG,▱EBFG与▱ABCD的相似比为23,连接CG,DG.若▱ABCD的面积为30,则△CDG的面积为.图10三、解答题11.如图,已知四边形ABCD,以AD的中点为位似中心将它放大,使放大前后的两个图形对应线段的比为1∶2.12.如图,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)在图中画出位似中心点O,△ABC与△A'B'C'的相似比是.(2)以点O为位似中心,在方格纸中再画一个△A1B1C1,使它与△ABC的相似比等于2∶1.13.如图7,在平面直角坐标系中,△ABC各顶点的坐标分别是A(2,4),B(-4,2),C(-2,-2).图7(1)以原点O为位似中心,画出一个△A1B1C1,使它与△ABC的相似比为1∶2;(2)根据(1)中的作图,△A1B1C1各顶点的坐标分别为A1,B1,C1.14.如图11,在正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(-3,2)和(1,-1),求这两个正方形的位似中心的坐标.图11参考答案1.B2.A3.D4.A5.C657.(6,6)8.y=-89.(3,2)10.5.11.解:(答案不唯一)如图所示,四边形A1B1C1D1即为所求.12.解:(1)点O如图所示.∵OA∶OA'=6∶12=1∶2,∴△ABC与△A'B'C'的相似比为1∶2.(2)△A1B1C1如图所示.13.解:答案不唯一.(1)如图所示,△A1B1C1即为所求.(2)(1,2)(-2,1)(-1,-1)14.解:当位似中心在两个正方形之间时,如图①,连接AF,DG交于点H,则点H为其位似中心,且点H在x轴上.∵DC∥GO,∴△DCH∽△GOH,∴ ‹ ‹=‹吠‹吠.由题意,得DC=2,GO=1,∴CH=2OH,∴OH=13OC.又∵D(-3,2),∴C(-3,0),∴OC=3,∴OH=1,∴其位似中心的坐标为(-1,0).当位似中心在正方形OEFG的右侧时,如图②,连接DE并延长,连接CF并延长,两条延长线交于点M,则点M为其位似中心,过点M作MN⊥x轴于点N,则CD∥EF∥MN,∴△MEF∽△MDC,△CED∽△NEM,∴ 〼 ‹= ‵ ‵, ‵= ‹ 吠= ‹‵吠.由题意,得DC=2,EF=1,∴ ‵ ‵= 〼 ‹=12,∴ED=EM,∴EC=EN,MN=DC=2.∵OC=3,OE=1,∴EC=4,∴ON=OE+EN=OE+EC=5,∴位似中心点M的坐标为(5,-2).综上所述,这两个正方形的位似中心的坐标为(-1,0)或(5,-2).。

图形的位似【学习目标】1、了解位似多边形的概念，知道位似变换是特殊的相似变换，能利用位似的方法，将一个图形放大或缩小；2、能在同一坐标系中，感受图形放缩前后点的坐标的变化.【要点梳理】要点一、位似多边形1.位似多边形定义:如果两个相似多边形任意一组对应顶点所在的直线都经过同一个点O，且每组对应点与点O 点的距离之比都等于一个定值k，例如，如下图，OA′=k·OA（k≠0），那么这样的两个多边形叫做位似多边形，点O叫做位似中心.要点诠释：位似图形与相似图形的区别：位似图形是一种特殊的相似图形，而相似图形未必能构成位似图形.2.位似图形的性质:（1）位似图形的对应点相交于同一点，此点就是位似中心；（2) 位似图形的对应点到位似中心的距离之比等于相似比；（3）位似图形中不经过位似中心的对应线段平行.3.平移、轴对称、旋转和位似四种变换的异同：图形经过平移、旋转或轴对称的变换后，虽然对应位置改变了，但大小和形状没有改变，即两个图形是全等的；而位似变换之后图形是放大或缩小的，是相似的．4.作位似图形的步骤第一步：在原图上找若干个关键点，并任取一点作为位似中心；第二步：作位似中心与各关键点连线；第三步：在连线上取关键点的对应点，使之满足放缩比例；第四步：顺次连接各对应点.要点诠释：位似中心可以取在多边形外、多边形内，或多边形的一边上、或顶点，下面是位似中心不同的画法.要点二、坐标系中的位似图形在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘同一个数k (k ≠0)，所对应的图形与原图形位似，位似中心是坐标原点，它们的相似比为|k |.要点诠释：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标等于原来点的坐标乘以（或除以）k 或-k.【典型例题】类型一、位似多边形例1. 下列每组的两个图形不是位似图形的是（ ）.A. B. C. D.【答案】D【解析】解：对应顶点的连线相交于一点的两个相似多边形叫位似图形．据此可得A 、B 、C 三个图形中的两个图形都是位似图形；而D 的对应顶点的连线不能相交于一点，故不是位似图形．故选D ．举一反三【变式】在小孔成像问题中， 根据如图4所示，若O 到AB 的距离是18cm ，O 到CD 的距离是6cm ，则像CD 的长是物AB 长的 （ ）.A. 3倍B.21 C.31 D.不知AB 的长度，无法判断【答案】C例2. 利用位似图形的方法把五边形ABCDE 放大1.5倍.【答案与解析】即是要画一个五边形A ′B ′C ′D ′E ′，要与五边形ABCDE 相似且相似比 为1.5.画法是：1．在平面上任取一点O.2．以O 为端点作射线OA 、OB 、OC 、OD 、OE.3．在射线OA 、OB 、OC 、OD 、OE 上分别取点A ′、B ′、C ′、D ′、E ′，使OA ′:OA ＝ OB ′:OB ＝OC ′:OC ＝OD ′:OD ＝OE ′:OE ＝1.5.4．连结A ′B ′、B ′C ′、C ′D ′、D ′E ′、E ′A ′.这样：A ′B ′AB ＝B ′C ′BC ＝C ′D ′CD ＝D ′E ′DE ＝A ′E ′AE＝1.5. 则五边形A ′B ′C ′D ′E ′为所求. 另外一种情况，所画五边形跟原五边形分别在位似中心的两侧.【总结升华】由本题可知，利用位似的方法，可以把一个多边形放大或缩小.举一反三【变式】在已知三角形内求作内接正方形．A 1B 1C 1D 1E 1 A B C DE【答案与解析】作法：（1）在AB 上任取一点G ′，作G ′D ′⊥BC；（2）以G ′D ′为边，在△ABC 内作一正方形D ′E ′F ′G ′；（3）连接BF ′，延长交AC 于F ；（4）作FG∥CB，交AB 于G ，从F 、G 分别作BC 的垂线FE ， GD ；∴四边形DEFG 即为所求．类型二、坐标系中的位似图形例3.如图，在10×10的正方形网格中，点A ，B ，C ，D 均在格点上，以点A 为位似中心画四边形AB ′C ′D ′，使它与四边形ABCD 位似，且相似比为2．（1）在图中画出四边形AB ′C ′D ′；（2）填空：△AC ′D ′是 三角形．【思路点拨】（1）延长AB 到B ′，使AB ′=2AB ，得到B 的对应点B ′，同样得到C 、D 的对应点C ′，D ′，再顺次连接即可；（2）利用勾股定理求出AC ′2=42+82=80，AD ′2=62+22=40，C ′D ′2=62+22=40，那么AD ′=C ′D ′，AD ′2+C ′D ′2=AC ′2，即可判定△AC ′D ′是等腰直角三角形．【答案与解析】解：（1）如图所示：B C（2）∵AC′2=42+82=16+64=80，AD′2=62+22=36+4=40，C′D′2=62+22=36+4=40，∴AD′=C′D′，AD′2+C′D′2=AC′2，∴△AC′D′是等腰直角三角形．故答案为：等腰直角．例4.如图△ABC的顶点坐标分别为A（1，1），B（2，3），C（3，0）．（1）以点O为位似中心画△DEF，使它与△ABC位似，且相似比为2．（2）在（1）的条件下，若M（a，b）为△ABC边上的任意一点，则△DEF的边上与点M 对应的点M′的坐标为．【思路点拨】（1）把点A、B、C的横、纵坐标都乘以2可得到对应点D、E、F的坐标，再描点可得△DEF；把点A、B、C的横、纵坐标都乘以﹣2可得到对应点D′、E′、F′的坐标，然后描点可得△D′E′F′；（2）利用以原点为位似中心的位似变换的对应点的坐标特征求解．【答案与解析】解：（1）如图，△DEF和△D′E′F′为所作；（2）点M对应的点M′的坐标为（2a，2b）或（﹣2a，﹣2b）．故答案为（2a，2b）或（﹣2a，﹣2b）．举一反三：【变式】如图，将△AOB中各顶点的纵坐标，横坐标分别乘-1，•得到的图形与原图形相比有什么变化？作出所得的图形，这个过程可以看作是一个什么图形变换？【答案】解：图形的形状和大小都没有变化；可以看作是△AOB绕O•点按逆时针方向旋转180°得到的.【巩固练习】一. 选择题1.下面给出了相似的一些命题：（1）菱形都相似；（2）等腰直角三角形都相似；（3）正方形都相似；（4）矩形都相似；（5）正六边形都相似；其中正确的有（）.A．2个 B．3个 C．4个 D．5个2.下列说法错误的是（）.A.位似图形一定是相似图形.B.相似图形不一定是位似图形.C.位似图形上任意一对对应点到位似中心的距离之比等于相似比.D.位似图形中每组对应点所在的直线必相互平行.3.下列说法正确的是（） .A.分别在ABC的边AB、AC的反向延长线上取点D、E，使DE∥BC，则ADE是ABC放大后的图形.B.两位似图形的面积之比等于相似比.C.位似多边形中对应对角线之比等于相似比.D.位似图形的周长之比等于相似比的平方.4．如图，在平面直角坐标系中，已知点A（﹣3，6），B（﹣9，﹣3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（）A．（﹣1，2）B．（﹣9，18）C．（﹣9，18）或（9，﹣18）D．（﹣1，2）或（1，﹣2）5. 下列命题：①两个正方形是位似图形；②两个等边三角形是位似图形；③两个同心圆是位似图形；④平行于三角形一边的直线截这个三角形的两边，所得的三角形与原三角形是位似图形.其中正确的有( ).A.1个B.2个C.3个D.4个二. 填空题8. 如果两个位似图形的对应线段长分别为3cm 和5cm ，且较小图形周长为30cm ，则较大图形周长为__________.9.如图，在平面直角坐标系中，已知A （1，0），D （3，0），△ABC 与△DEF 位似，原点O 是位似中心．若AB=1.5，则DE= ．10．如图，以点O 为位似中心，将五边形ABCDE 放大后得到五边形，已知OA =10cm ，OA ′=20cm ，则五边形ABCDE 的周长与五边形的周长的比值是__________．11. △ABC 中，D 、E 分别在AB 、AC 上，DE ∥BC ，△ADE 是△ABC 缩小后的图形.若DE 把△ABC 的面积分成相等的两部分，则AD ：AB=________.12. 把一矩形纸片对折，如果对折后的矩形与原矩形相似，则原矩形纸片的长与宽之比为____________________.13.如图，以O 为位似中心，将边长为256的正方形OABC 依次作位似变换，经第一次变化后得正方形OA 1B 1C 1，其边长OA 1缩小为OA 的，经第二次变化后得正方形OA 2B 2C 2，其边长OA 2缩小为OA 1的，经第，三次变化后得正方形OA 3B 3C 3，其边长OA 3缩小为OA 2的，…，依次规律，经第n 次变化后，所得正方形OA n B n C n 的边长为正方形OABC 边长的倒数，则n= ．A B C D E '''''A B C D E '''''14. 如图，△ABC中，AB=AC=4，∠BAC=36°，∠ABC的平分线与AC边的交点D为边AC的黄金分割点（AD＞DC），则BC=______________.三．综合题15.如图，D、E分别AB、AC上的点.(1)如果DE∥BC，那么△ADE和△ABC是位似图形吗？为什么？(2)如果△ADE和△ABC是位似图形，那么DE∥BC吗？为什么？16.如图，F在BD上，BC、AD相交于点E，且AB∥CD∥EF，（1）图中有哪几对位似三角形，选其中一对加以证明；（2）若AB=2，CD=3，求EF的长．17. 如图1，矩形ODEF 的一边落在矩形ABCO 的一边上，并且矩形ODEF ∽矩形ABCO ，其相（1）求矩形ODEF 的面积；（2）将图1中的矩形ODEF 绕点O 逆时针旋转一周，连接EC 、EA ，△ACE 的面积是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，请说明理由．【答案与解析】一、选择题1．【答案】B【解析】（1）菱形的角不一定对应相等，故错误；（2）（3）（5）符合相似的定义，故正确；（4）对应边的比不一定相等．故错误．故正确的是：（2）（3）（5）．故选B ．2．【答案】D.3．【答案】C.4.【答案】D.【解析】∵A （﹣3，6），B （﹣9，﹣3），以原点O 为位似中心，相似比为，把△ABO 缩小，∴点A 的对应点A ′的坐标为（﹣3×，6×）或[﹣3×（﹣），6×（﹣）]，即A ′点的坐标为（﹣1，2）或（1，﹣2）．5．【答案】B【解析】由位似图形的概念可知③和④对，故选B.6．【答案】D.【解析】∵AC ＞BC ，∴AC 是较长的线段，AC ≈0.618AB ．故选D ．7.【答案】B.【解析】∵AB=1，设AD=x ，则FD=x-1，FE=1，∵四边形EFDC 与矩形ABCD 相似， AB AC，二、填空题 8.【答案】50cm. 9.【答案】4.5．【解析】∵△ABC与DEF 是位似图形，它们的位似中心恰好为原点，已知A 点坐标为（1，0），D 点坐标为（3，0），∴AO=2，DO=5，∴==，∵AB=1.5，∴DE=4.5．故答案为：4.5．10.【答案】1：2．【解析】∵五边形ABCDE 与五边形A ′B ′C ′D ′E ′位似，OA=10cm ，OA ′=20cm ，∴五边形ABCDE ∽五边形A ′B ′C ′D ′E ′，且相似比为：OA ：OA ′=10：20=1：2， ∴五边形ABCDE 的周长与五边形A ′B ′C ′D ′E ′的周长的比为：OA ：OA ′=1：2． 故答案为：1：2．11.【答案】 .【解析】由BC ∥DE 可得△ADE ∽△ABC ，所以，故.111x x =-13. 【答案】16.【解析】由图形的变化规律可得×256=， 解得n=16．14. 【解析】∵AB=AC，∠A=36°，∴∠ABC=∠C=72°，又BD 平分∠ABC ，∴∠ABD=∠CBD=36°，∴∠BDC=72°，∴BC=BD=AD ，∵D 点是AC 的黄金分割点，三．解答题15.【答案与解析】(1)△ADE 和 △ABC 是位似图形.理由是：DE ∥BC ，所以∠ADE=∠B ， ∠AED=∠C.所以△ADE ∽△ABC ，所以. 又因为 点A 是△ADE 和 △ABC 的公共点，点D 和点B 是对应点，点E 和点C是对应点，直线BD 与CE 交于点A ，所以△ADE 和 △ABC 是位似图形.(2)DE ∥BC.理由是：因为△ADE 和△ABC 是位似图形，所以△ADE ∽△ABC所以∠ADE=∠B所以DE ∥BC.16.【答案与解析】解：（1）△DFE 与△DBA ，△BFE 与△BDC ，△AEB 与△DEC 都是位似图形， 理由：∵AB ∥CD ∥EF ，∴△DFE ∽△DBA ，△BFE ∽△BDC ，△AEB ∽△DEC ，且对应边都交于一点，∴△DFE与△DBA，△BFE与△BDC，△AEB与△DEC都是位似图形；（2）∵△BFE∽△BDC，△AEB∽△DEC，AB=2，CD=3，∴==，∴==，解得：EF=．17.【答案与解析】（1）∵矩形ODEF∽矩形ABCO，其相似比为1：4，（2）存在．。

6.6图形的位似同步练习一．选择题1．如图，正方形ABCD和正方形EFOG是位似图形，其中点A与点E对应，点A的坐标为（﹣4，2）点E的坐标为（﹣1，1），则这两个正方形位似中心的坐标为（）A．（2，0）B．（1，1）C．（﹣2，0）D．（﹣1，0）2．如图，六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形，O为位似中心，OD＝OD1，则A1B1：AB为（）A．2：3B．3：2C．1：2D．2：13．如图，四边形ABCD与四边形A'B'C'D'位似，点O为位似中心，若OB：OB'＝2：3，则四边形ABCD与四边形A'B'C′D'的面积比为（）A．2：3B．2：5C．4：9D．4：254．在平面直角坐标系中，△ABC顶点A（2，3），若以原点O为位似中心，画三角形ABC 的位似图形△A′B′C′，使△A′B′C′与△ABC的相似比为1：2，则A′的坐标为（）A．（1，）B．（2，6）C．（1，）或（﹣1，﹣）D．（2，6）或（﹣2，﹣6）5．如图，在△ABC中，A、B两个顶点在x轴的上方，点C的坐标是（﹣1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B'C′，并把△ABC的边长放大到原来的2倍．设点B的对应点B′的横坐标是a，则点B的横坐标是（）A．﹣B．C．D．6．下列说法错误的是（）A．如果把一个多边形的面积扩大为原来的5倍，那么它的各边也扩大为原来的5倍B．如果把一个三角形的各边扩大为原来的5倍，那么它的周长也扩大为原来的5倍C．相似三角形对应高的比等于对应中线的比D．相似多边形的面积比等于周长比的平方7．如图，△ABC中，三个顶点的坐标分别是A（﹣2，2），B（﹣4，1），C（﹣1，﹣1）．以点C为位似中心，在x轴下方作△ABC的位似图形△A'B'C'，并把△ABC的边长放大为原来的2倍，那么点A'的坐标为（）A．（3，﹣7）B．（1，﹣7）C．（4，﹣4）D．（1，﹣4）8．在如图所示的网格中，以点O为位似中心，四边形ABCD的位似图形是（）A．四边形NPMQ B．四边形NPMR C．四边形NHMQ D．四边形NHMR 9．如图，△ABC与△A1B1C1是以O为位似中心的位似图形，若OA＝3AA1，S△ABC＝36，则S＝（）A．64B．68C．81D．9210．如图，等腰Rt△ABC与等腰Rt△CDE是以点O为位似中心的位似图形，位似比为k＝1：3，∠ACB＝90°，BC＝4，则点D的坐标是（）A．（18，12）B．（16，12）C．（12，18）D．（12，16）二．填空题11．已知：如图，E（﹣6，2），F（﹣2，﹣2），以原点O为位似中心，相似比1：2，把△EFO在y右侧缩小，则点E的对应点E1的坐标为．12．如图，在平面直角坐标系中，正方形OABC与正方形ODEF是位似图形，点O为位似中心，位似比为2：3，点B、E在第一象限，若点A的坐标为（4，0），则点E的坐标是．13．如图，在平面直角坐标系中，已知点A（﹣2，4），B（﹣8，﹣2），以原点O为位似中心，在y轴的右侧把线段AB缩小为原来的，则点A的对应点A′的坐标是．14．如图，在平面直角坐标系中有两点A（6，0）和B（6，3），以原点O为位似中心，相似比为，把线段AB缩短为CD，其中点C与点A对应，点D与点B对应，且CD在y 轴的右侧，则点D的坐标为．15．如图，在平面直角坐标系中，等边△ABC与等边△BDE是以原点为位似中心的位似图形，且相似比为，点A、B、D在x轴上，若等边△BDE边长为6，则点C的坐标为．三．解答题16．已知：△ABC三个顶点的坐标分别为A（﹣2，﹣2），B（﹣5，﹣4），C（﹣1，﹣5）．（1）画出将△ABC绕点A逆时针旋转90°的△AB1C1；（2）以点O为位似中心，将△ABC放大为原来的2倍，得到△A2B2C2，请在网格纸中画出△A2B2C2，并写出点C2的坐标．（3）若图中每个小方格的面积为1，请直接写出△A2B2C2的面积．17．如图，△ABC各顶点坐标分别为：A（﹣4，4），B（﹣1，2），C（﹣5，1）．（I）以O为位似中心，在x轴下方将△ABC放大为原来的2倍形成△A2B2C2；（2）求S．18．如图，已知O为坐标原点，B，C两点坐标为（3，﹣1），（2，1）．（1）在y轴的左侧将△OBC放大到原来的2倍，画出放大后△O1B1C1；（2）写出B1，C1的坐标；（3）在（1）条件下，若△OBC内部有一点M的坐标为（x，y），写出M的对应点M1的坐标．参考答案一．选择题1．解：连接AE并延长交x轴于H，则点H为位似中心，∵点A的坐标为（﹣4，2）点E的坐标为（﹣1，1），∴OF＝1，OB＝4，EF＝1，AB＝2，∵正方形ABCD和正方形EFOG是位似图形，∴EF∥AB，∴△HEF∽△HAB，∴＝，即＝，解得，OH＝2，∴点H的坐标为（2，0），故选：A．2．解：∵六边形ABCDEF与六边形A1B1C1D1E1F1是位似图形，∴六边形ABCDEF∽六边形A1B1C1D1E1F1，DE∥D′E′，∴△ODE∽△OD1E1，∴＝＝，∴＝＝2：1，故选：D．3．解：∵四边形ABCD与四边形A'B'C'D'位似，∴四边形ABCD∽四边形A'B'C'D'，AB∥A′B′，∴△OAB∽△OA′B′，∴＝＝，∴四边形ABCD与四边形A'B'C′D'的面积比＝（）2＝，故选：C．4．解：∵以原点O为位似中心，画三角形ABC的位似图形△A′B′C′，使△A′B′C′与△ABC的相似比为1：2，点A（2，3），∴A′的坐标为（2×，3×）或（﹣2×，﹣3×），即（1，）或（﹣1，﹣），故选：C．5．解：以点C为坐标原点建立新的坐标系，∵点C的坐标是（﹣1，0），∴点B′的横坐标为：a+1，以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B'C′，则点B在以C为坐标原点的坐标系中的横坐标为：﹣，∴点B在原坐标系中的横坐标为：﹣﹣1＝﹣，故选：D．6．解：A、如果把一个多边形的面积扩大为原来的5倍，那么它的各边也扩大为原来的倍，本选项说法错误，符合题意；B、如果把一个三角形的各边扩大为原来的5倍，那么它的周长也扩大为原来的5倍，本选项说法正确，不符合题意；C、相似三角形对应高的比等于对应中线的比，本选项说法正确，不符合题意；D、相似多边形的面积比等于周长比的平方，本选项说法正确，不符合题意；故选：A．7．解：以C为坐标原点建立平面直角坐标系，则点A在新坐标系中的坐标为（﹣1，3），∵△ABC与△A'B'C'以点C为位似中心，在x轴下方作△ABC的位似图形△A'B'C'，把△ABC的边长放大为原来的2倍，∴点A'在新坐标系中的坐标为（1×2，﹣3×2），即（2，﹣6），则点A'的坐标为（1，﹣7），故选：B．8．解：∵以点O为位似中心，∴点C对应点M，设网格中每个小方格的边长为1，则OC＝＝，OM＝＝2，OD＝，OB＝＝，OA ＝＝，OR＝＝，OQ＝2，OP＝＝2，OH＝＝3，ON＝＝2，∵＝＝2，∴点D对应点Q，点B对应点P，点A对应点N，∴以点O为位似中心，四边形ABCD的位似图形是四边形NPMQ，故选：A．9．解：∵△ABC与△A1B1C1是以O为位似中心的位似图形，∴△ABC∽△A1B1C1，∵OA＝3AA1，∴△ABC与△A1B1C1的相似比为：＝，∴△ABC与△A1B1C1的面积比为：（）2＝，∵S△ABC＝36，∴S＝36÷＝64，故选：A．10．解：由题意可得：△OBC∽△ODE，则＝＝，∵BC＝4，∴ED＝12，∵等腰Rt△CDE，∴CE＝DE＝12，∴＝，解得：CO＝6，故EO＝18，∴点D的坐标是（18，12）．故选：A．二．填空题11．解：∵以原点O为位似中心，相似比1：2，把△EFO在y右侧缩小，E（﹣6，2），∴点E的对应点E1的坐标为（6×，﹣2×），即（3，﹣1），故答案为：（3，﹣1）．12．解：∵正方形OABC与正方形ODEF是位似图形，点O为位似中心，位似比为2：3，∴＝，＝，即＝，＝，解得，OD＝6，OF＝6，则点E的坐标为（6，6），故答案为：（6，6）．13．解：∵以原点O为位似中心，在y轴的右侧把线段AB缩小为原来的，点A的坐标为（﹣2，4），∴点A的对应点A′的坐标为（﹣2×（﹣），4×（﹣）），即（1，﹣2），故答案为：（1，﹣2）．14．解：∵以原点O为位似中心，相似比为，把线段AB缩短为CD，CD在y轴的右侧，点B的坐标为（6，3），∴点D的坐标为（6×，3×），即（3，），故答案为：（3，）．15．解：作CF⊥AB于F，∵等边△ABC与等边△BDE是以原点为位似中心的位似图形，∴BC∥DE，∴△OBC∽△ODE，∴＝，∵△ABC与△BDE的相似比为，等边△BDE边长为6，∴＝＝，解得，BC＝2，OB＝3，∴OA＝1，∵CA＝CB，CF⊥AB，∴AF＝1，由勾股定理得，CF＝＝，∴OF＝OA+AF＝2，∴点C的坐标为（2，），故答案为：（2，）．三．解答题16．解：（1）如图，△AB1C1为所作；（2）如图，△A2B2C2为所作；点C2的坐标为（2，10）．（3）△A2B2C2的面积＝4S△ABC＝4（4×3﹣×1×3﹣×3×2﹣×1×4）＝22．17．解：（1）如图，△A2B2C2为所作；（2）S＝6×8﹣×6×2﹣×8×2﹣×4×6＝22．18．解：（1）如图，△O1B1C1即为所求作．（2）B1（﹣6，2），C1（﹣4，﹣2）．（3）M1（﹣2x，﹣2y）．。

第66讲 位似题一： 用两种方法，以O 为位似中心，把△ABC 缩小为原来的．题二： 以点O 为位似中心，将网格中的图形放大为原来的2倍．题三： 如图，△ABC 在方格中．(1)请在方格纸上建立平面直角坐标系，使A (2，3)、C (5，2)，并求出B 点坐标；(2)以原点O 为位似中心，相似比为2，在第一象限内将△ABC 放大，画出放大后的图形．题四： 如图，在平面直角坐标系中，四边形ABCD 的四个顶点的坐标分别是A (1，3)、B (2，2)、C (2，1)，D (3，3)．(1)以原点O 为位似中心，相似比为2，将图形放大，画出符合要求的位似四边形；(2)在(1)的前提下，写出点A 的对应点坐标，并说明点A 与点坐标的关系．12A 'A '题五： 如图，△ABC 的两个顶点BC 均在第一象限，以点A (0，1)为位似中心，在y 轴左方作△ABC 的位似图形△，△ABC 与△的位似比为1：2．若设点C 的纵坐标是m ，则其对应点的纵坐标是( )A ．－(2m －3)B ．－(2m －2)C ．－(2m －1)D ．－2m题六： 如图，△ABC 中，A ，B 两个顶点在x 轴的上方，点C 的坐标是(－1，0)．将△ABC 绕C 点按顺时针方向旋转180°后，记所得的图形是△NMC ．设点M 的横坐标是a ，则点B 的横坐标是( )A ．－aB ．－(a +1)C ．－(a －1)D ．－(a +2)第66讲位似题一： 见详解．详解：如图所示，△与△即为所求．AB C ''AB C ''C'A B C '''A B C ''''''题二： 见详解．详解：作图如下：题三： 见详解．详解：(1)如图画出原点O 、x 轴、y 轴，建立直角坐标系， 则B 的坐标为 (2，1)；(2)如图，△即为所求．题四： 见详解．详解：(1)符合要求的位似四边形有两个，如图所示．A B C '''(2)点A 的对应点有2个，分别是(2，6)或(－2，－6)， 其中点的横、纵坐标分别是点A 的横、纵坐标分别乘以2或－2． 题五： A ．详解：设点C 的纵坐标为m ，则A 、C 间的纵坐标的长度为(m －1)， ∵△ABC 放大到原来的2倍得到△，∴、A 间的纵坐标的长度为2 (m －1)，∴点的纵坐标是－[2(m －1)－1]=－(2m －3)．故选A ．题六： D ．详解：过B 点和M 点作x 轴的垂线，垂足分别是D 和E ，∵点M 的横坐标是a 点，C 的坐标是 (－1，0)．∴EC = a +1， 又∵△CNM 的边长与△ABC 的边长相等，∴DC =a +1，∴DO =a +2，∴B 点的横坐标是－(a +2)．故选D ．A 'A 'A 'A 'ABC ''C 'C'。

6.6《图形的位似》一、选择题1.下列说法正确的是（）A.分别在△4BC的边4C的反向延长线上取点D, E,使DE//BC,则△力DE是△ 4BC放大后的图形B.两位似图形的面积之比等于位似比C.位似多边形中对应对角线之比等于位似比D.位似图形的周长Z比等于位似比的平方如图，以点O为位似中心，将△SBC缩小后得到△ xire,已知SJ 3CW, 则与的面积的比为（）A.1： 3B.1： 4C.1： 5D.1： 9如图，在平面直角坐标系中，已知点0（0, 0）, 4（6, 0）, B（0, 8）,以某点为位似屮心，作出与△MB的位似比为R的位似厶CDE,贝IJ位似屮心的坐标和«的值分别为（）A.(0, 0), 21B.(2, 2),-C.(2, 2), 21D.(1, 1),-2.3.4.如图△SBC与ADEF是位似图形，位似比是1： 2,已知DE = 4,则A3的长是（）6. A. 2 B.4DC. 8D. 1B（易错题）如图，将△MBC的三边缩小为原来的*任取一点0,连A0、C0,并収它们的中点D、E、F,得△DEF,下列说法正确的个数是（①△力BC与△ DEF是位似图形B（?）△ ABC与△ DEF是相似图形（3） A ABC与△DEF周长之比为2： 1（4）^ ABC与△ DEF的面积之比为4： 1.A.l个B. 2个C. 3个D.4个平面直角坐标系屮，有一条鱼，它有六个顶点，贝M ）A.将各点横坐标乘以2,纵坐标不变，得到的鱼与原来的鱼位似B.将各点纵坐标乘以2,横坐标不变，得到的鱼与原来的鱼位似C.将各点横，纵坐标都乘以2,得到的鱼与原来的鱼位似D.将各点横坐标乘以2,纵坐标乘以*,得到的鱼与原來的鱼位似如图，△4B0与厶A'B'O是位似图形，其“MB//AE,那么力®的长y 与AB的长兀之间函数关系的图象大致是（）A.B'8. 已知“ABC 与厶4/1"位似，A/IBC 与厶A 2B 2C 2位似，贝lj()A. A 1B 1C 1 与彳 A 2B 2C 2全等B. △力iB]C]与△ A 2B 2C 2位似C. △出与△ A 2B 2C 2相似但不一定位似D.与公A 2B 2C 2不相似9.已知点A 的坐标是(2, 1),以坐标原点O 为位似中心，像与原图形的位似比为2,则点A 的坐标为()10. 下列3个图形中是位似图形的有()1A. (1, 2} 1 、 1C. (1, R 或(-1,--) B. (4, 2)D. (4, 2)或(-4, -2)A. 0个C.2个 C二、解答题11.如图，在平面直角坐标系兀0)：中，AABC的三个顶点分别为4(2, 6), B(4, 2), C(6, 2).1⑴以原点O为位似中心，将△力BC缩小为原来的亍得到△DEF.请在第一象限内，画出△DEF.(2)在(1)的条件下，点A的对应点D的坐标为_______ ，点B的对应点E的坐标为_______12.如图，在边长均为1的小正方形网格纸中，厶0力B的顶点0、4、3均在格点上，且O是直角坐标系的原点，点A在x轴上.(1)以0为位似中心，将△0M放大，使得放大后的△ 04卫1,与△04〃对应线段的比为2： 1,画出△。

苏科版九年级下册数学第6章图形的相似含答案一、单选题(共15题，共计45分)1、如下图，已知⊙O的直径为AB，AC⊥AB于点A, BC与⊙O相交于点D，在AC 上取一点E，使得ED=EA．下面四个结论：①ED是⊙O的切线；②BC=2OE③△BOD为等边三角形；④△EOD ∽△CAD，正确的是（）A.①②B.②④C.①②④D.①②③④2、如图，平行于BC的直线DE把△ABC分成面积相等的两部分，则的值为（）A.1B.C. -1D. +13、如图，在△ABC中，若DE∥BC，=，DE=4cm，则BC的长为（）A.8cmB.12cmC.11cmD.10cm4、图中两个四边形是位似图形，它们的位似中心是（）A.点MB.点NC.点OD.点P5、已知△ABC中，∠C=90°，tanA= ，D是AC上一点，∠CBD=∠A，则sin∠ABD=（）A. B. C. D.6、如图，平面直角坐标系中，，反比例函数的图象分别与线段交于点，连接.若点关于的对称点恰好在上，则（）A. B. C. D.7、下列命题中，正确的是（）A.所有的等腰三角形都相似B.所有的直角三角形都相似C.所有的等边三角形都相似D.所有的矩形都相似8、下列命题中，正确的个数是（）①等边三角形都相似；②直角三角形都相似；③等腰三角形都相似；④锐角三角形都相似；⑤等腰三角形都全等；⑥有一个角相等的等腰三角形相似；⑦有一个钝角相等的两个等腰三角形相似；⑧全等三角形相似．A.2个B.3个C.4个D.5个9、一组正方形按如图所示的方式放置，其中顶点B1在y轴上，顶点C1、E1、E 2、C2、E3、E4、C3…在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O=60°，B 1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是（）A.（）2015B.（）2016C.（）2016D.（）201510、若2a=3b，则的值为( )A. B. C. D.11、宽与长的比是（约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形：作正方形，分别取的中点，连接，以点F为圆心，以为半径画弧，交的延长线于点G；作，交的延长线于点H，则图中下列矩形是黄金矩形的是（）A.矩形ABEFB.矩形EFCDC.矩形EFGHD.矩形ABGH12、如图，在△ABC中，点D，E分别在边AB，AC上，且DE∥BC，，若S△ADE ＝2，则S△ABC的值是（）A.6B.8C.18D.3213、如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中：①CE=BD；②△ADC是等腰直角三角形；③∠ADB=∠AEB；④CD•AE=EF•CG；一定正确的结论有（）A.1个B.2个C.3个D.4个14、如图，在中，，将沿图示中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（）A.  B.C.D.15、已知：如图，在△ABC中，∠AED＝∠B，则下列等式成立的是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，是小彬利用标杆AB测量某建筑物高度的示意图，其中P，B，D在同一水平直线上，点P，A，C在同一直线上，AB⊥PD，CD⊥PD，测得标杆AB=1.5m，PB=2m，PB=6m，则该建筑物CD的高是________米．17、如图所示，一般书本的纸张是原纸张多次对开得到的，矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依此类推，若各种开本的矩形都相似，那么等于________ ．18、在Rt△ABC中∠C=90°，AD平分∠CAB,BE平分∠CBA,AD、BE相交于点F，且AF=4,EF= ,则AC=________．19、如图，与中，，，，，AD的长为________.20、如果△ABC∽△DEF，且△ABC的面积为2cm2，△DEF的面积为8cm2，那么△ABC与△DEF相似比为________．21、在比例尺为1∶20000的地图上，相距3cm的A、B两地的实际距离是________22、如图，5个同样大小的正方形拼成一个长方形，则________.23、如图：AB、CD相交于O，且∠A=∠C，若OA=3，OD=4，OB=2，则OC=________.24、如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是________25、如图，电灯在横杆的正上方，在灯光下的影子为，，米，米，点到的距离是3米，则到的距离是________米.三、解答题(共5题，共计25分)26、，求的值.27、附加题：如图，在中，，，垂足为，、分别为、的中点，，垂足为，求证：．28、如图，已知，，，求的度数．29、如图，在直角坐标系中，△ABC是格点三角形（三角形的三个顶点都是小正方形的顶点）．（1）在第一象限内找一点P，以格点P、A、B为顶点的三角形与△ABC相似但不全等，请写出符合条件格点P的坐标；（2）请用直尺与圆规在第一象限内找到两个点M、N，使∠AMB=∠ANB=∠ACB．请保留作图痕迹，不要求写画法．30、如图，矩形ABCD中，E为BC上一点，DF⊥AE于F．（1）△ABE与△ADF相似吗？请说明理由．（2）若AB=6，AD=12，BE=8，求DF的长．参考答案一、单选题(共15题，共计45分)1、C2、C3、B4、D5、A6、C7、C8、B9、D10、D11、D12、C13、D14、D15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、23、24、25、三、解答题(共5题，共计25分)26、29、。