数字电子技术基础第三章逻辑门电路
- 格式:ppt
- 大小:4.12 MB
- 文档页数:37

数字电子技术基础课后答案全解第3章逻辑代数及逻辑门【3-1】填空1、与模拟信号相比,数字信号的特点是它的离散性。
一个数字信号只有两种取值分别表示为0和12、布尔代数中有三种最基本运算:与、或和非,在此基础上又派生出五种基本运算,分别为与非、或非、异或、同或和与或非。
3、与运算的法则可概述为:有“0”出0,全“1”出1;类似地或运算的法则为有”1”出”1”,全”0”出”0”4、摩根定理表示为:AB=AB;AB=AB。
5、函数表达式Y=ABCD,则其对偶式为Y=(AB)CD。
6、根据反演规则,若Y=ABCDC,则Y(ABCD)C7、指出下列各式中哪些是四变量ABCD的最小项和最大项。
在最小项后的()里填入mi,在最大项后的()里填入Mi,其它填某(i为最小项或最大项的序号)。
(1)A+B+D(某);(2)ABCD(m7);(3)ABC(某)(4)AB(C+D)(某);(5)ABCD(M9);(6)A+B+CD(某);8、函数式F=AB+BC+CD写成最小项之和的形式结果应为成最大项之积的形式结果应为m(3,6,7,11,12,13,14,15),写M(0,1,2,4,5,8,9,10)9、对逻辑运算判断下述说法是否正确,正确者在其后()内打对号,反之打某。
(1)若某+Y=某+Z,则Y=Z;(某)(2)若某Y=某Z,则Y=Z;(某)(3)若某Y=某Z,则Y=Z;(√)【3-2】用代数法化简下列各式(1)F1=ABCAB1(2)F2=ABCDABDACDAD(3)F3ACABCACDCD(4)F4ABC(ABC)(ABC)ACD【3-3】用卡诺图化简下列各式ABC(1)F1BCABABC(2)F2ABBCBCABCAB(3)F3ACACBCBC(4)F4ABCABDACDCDABCACDABACBCAD第1页/共46页或ABACBC(5)F5ABCACABD(6)F6ABCDABCADABCABACBDABCCD(7)F7ACABBCDBDABDABCD(8)F8ACACBDBDABDBDABCDABCDABCDABCD(9)F9A(CD)BCDACDABCDCDCD(10)F10=F10ACABBCDBECDECABACBDEC【3-4】用卡诺图化简下列各式(1)P1(A,B,C)=m(0,1,2,5,6,7)ABACBCm(0,1,2,3,4,6,7,8,9,10,11,14)ACADBCDABBC ADBD(2)P2(A,B,C,D)=(3)P3(A,B,C,D)=m(0,1,,4,6,8,9,10,12,13,14,15)(4)P4(A,B,C,D)=M1M7ABCBCD【3-5】用卡诺图化简下列带有约束条件的逻辑函数(1)P1A,B,C,Dm(3,6,8,9,11,12)d(0,1,2,13,14,15)ACBDBCD(或ACD)(2)P2(A,B,C,D)=m(0,2,3,4,5,6,11,12)(8,9,10,13,14,15)dBCBCD(3)P3=ACDABCDABCDADACDBCD(或ABD)AB+AC=0(4)P4=ABCDABCDAB(ABCD为互相排斥的一组变量,即在任何情况下它们之中不可能两个同时为1)【3-6】已知:Y1=ABACBDY2=ABCDACDBCDBC用卡诺图分别求出Y1Y2,Y1Y2,Y1Y2。




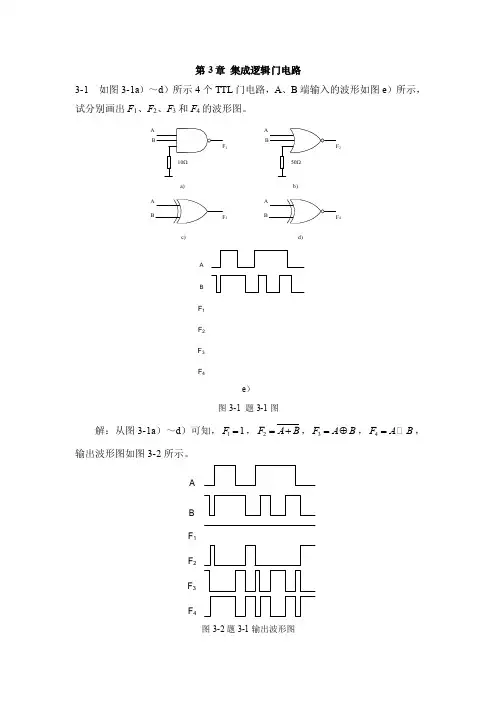
第3章集成逻辑门电路3-1 如图3-1a)~d)所示4个TTL门电路,A、B端输入的波形如图e)所示,试分别画出F1、F2、F3和F4的波形图。
A1A234a)b)c)d)F1F2F3F4BAe)图3-1 题3-1图解:从图3-1a)~d)可知,11F=,2F A B=+,3F A B=⊕,4F A B= ,输出波形图如图3-2所示。
F1F2F3F4AB图3-2题3-1输出波形图3-2 电路如图3-3a )所示,输入A 、B 的电压波形如图3-3b )所示,试画出各个门电路输出端的电压波形。
1A 23b)a)AB图3-3 题3-2图解:从图3-3a )可知,1F AB =,2F A B =+,3F A B =⊕,输出波形如图3-4所示。
F 1F 2F 3AB图3-4 题3-2输出波形3-3在图3-5a )所示的正逻辑与门和图b )所示的正逻辑或门电路中,若改用负逻辑,试列出它们的逻辑真值表,并说明F 和A 、B 之间是什么逻辑关系。
b)a)图3-5 题3-3图解:(1)图3-5a )负逻辑真值表如表3-1所示。
表3-1 与门负逻辑真值表F 与A 、B 之间相当于正逻辑的“或”操作。
(2)图3-5b )负逻辑真值表如表3-2所示。
表3-2 或门负逻辑真值表F 与A 、B 之间相当于正逻辑的“与”操作。
3-4试说明能否将与非门、或非门和异或门当做反相器使用?如果可以,各输入端应如何连接?解:与非门、或非门和异或门经过处理以后均可以实现反相器功能。
1)与非门:将多余输入端接至高电平或与另一端并联; 2)或非门:将多余输入端接至低电平或与另一端并联;3) 异或门:将另一个输入端接高电平。
3-5为了实现图3-6所示的各TTL 门电路输出端所示的逻辑关系,请合理地将多余的输入端进行处理。
b)a)AB=A B=+A BC DABC D图3-6 题3-5图解:a )多余输入端可以悬空,但建议接高电平或与另两个输入端的一端相连;b )多余输入端接低电平或与另两个输入端的一端相连;c) 未用与门的两个输入端至少一端接低电平,另一端可以悬空、接高电平或接低电平;d )未用或门的两个输入端悬空或都接高电平。


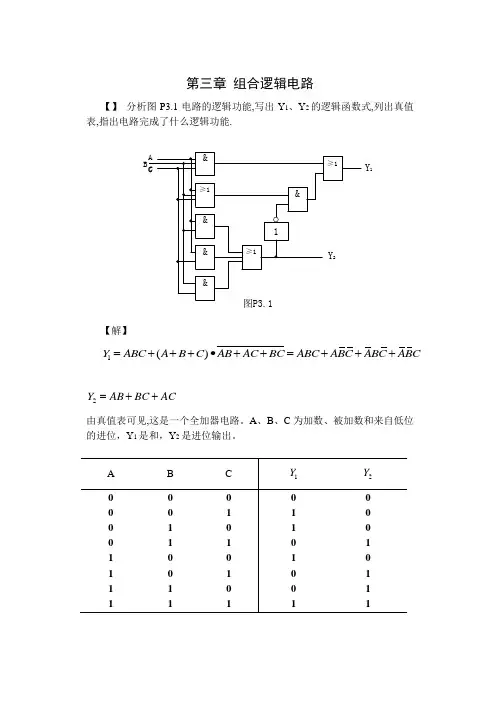
第三章 组合逻辑电路【】 分析图P3.1电路的逻辑功能,写出Y 1、Y 2的逻辑函数式,列出真值表,指出电路完成了什么逻辑功能.Y 1【解】1()Y ABC A B C AB AC BC ABC ABC ABC ABC=+++•++=+++2Y AB BC AC =++由真值表可见,这是一个全加器电路。
A 、B 、C 为加数、被加数和来自低位的进位,Y 1是和,Y 2是进位输出。
【】 图3.2是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1;Z=0和COMP=0,Z=0时Y 1,Y 2,Y 3,Y 4的逻辑式,列出真值表。
Y 1Y 2Y 3Y 4A 1A 2A 3A 4Z【解】(1)COMP=1、Z=0时输出的逻辑式为11223234234Y A Y A Y A A Y A A A⎧=⎪=⎪⎨=⊕⎪⎪=++⎩ 〔2〕COMP=0、Z=0时输出的逻辑式为11223344Y A Y A Y A Y A =⎧⎪=⎪⎨=⎪⎪=⎩〔即不变换,真值表从略〕3个或3个以上为1时输出1,输入为其他状态时输出0。
【解】Y ABCD ABCD ABCD ABCD ABCD ABC ABD ACD BCD ABC ABD ACD BCD=++++=+++=•••B D Y【】 有一水箱由大、小两台水泵M L 、M S 供水,如图P3.4所示.水箱中设置了3个水位检测元件A、B 、C 。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作;水位低于C 点高于B 点时M S 单独工作;水位低于B 点而高于A 点时M L 单独工作;水位低于A 点时M L 、M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
【解】图P3.4M L真值表中的ABC 、ABC 、ABC 、ABC 为约束项,利用卡诺图【图A3.4(a)】化简后得到S L M A BCM B⎧=+⎪⎨=⎪⎩ 〔M S 、M L 的1状态表示工作,0状态表示停止〕 逻辑图如图A3.4(b).S M A BC =+L M B =〔a 〕(b)A B CM SM L【】。

