数电-第三章_逻辑门电路

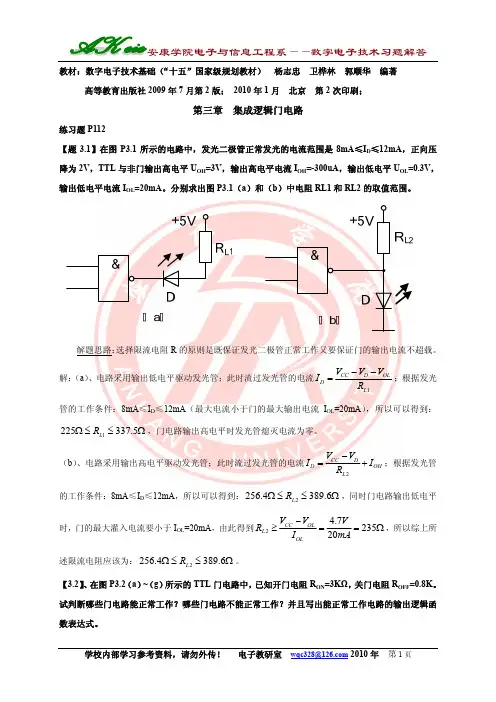
教材：数字电子技术基础（“十五”国家级规划教材） 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版； 2010年1月 北京 第2次印刷；第三章 集成逻辑门电路练习题P112【题3.1】在图P3.1所示的电路中，发光二极管正常发光的电流范围是8mA ≤I D ≤12mA ，正向压降为2V ，TTL 与非门输出高电平U OH =3V ，输出高电平电流I OH =-300uA ，输出低电平U OL =0.3V ，输出低电平电流I OL =20mA 。

分别求出图P3.1（a ）和（b ）中电阻RL1和RL2的取值范围。

解题思路：选择限流电阻R 的原则是既保证发光二极管正常工作又要保证门的输出电流不超载。

解：（a ）、电路采用输出低电平驱动发光管；此时流过发光管的电流1CC D OL D L V V V I R −−=；根据发光管的工作条件：8mA ≤I D ≤12mA （最大电流小于门的最大输出电流I OL =20mA ），所以可以得到：1225337.5L R Ω≤≤Ω，门电路输出高电平时发光管熄灭电流为零。

（b ）、电路采用输出高电平驱动发光管；此时流过发光管的电流2CC D D OH L V V I I R −=+；根据发光管的工作条件：8mA ≤I D ≤12mA ，所以可以得到：2256.4389.6L R Ω≤≤Ω，同时门电路输出低电平时，门的最大灌入电流要小于I OL =20mA ，由此得到2 4.723520CC OL L OL V V V R I mA−≥==Ω，所以综上所述限流电阻应该为：2256.4389.6L R Ω≤≤Ω。

【3.2】、在图P3.2（a ）~（g ）所示的TTL 门电路中，已知开门电阻R ON =3K Ω，关门电阻R OFF =0.8K 。

试判断哪些门电路能正常工作？哪些门电路不能正常工作？并且写出能正常工作电路的输出逻辑函数表达式。

解题思路：了解各类门电路的逻辑功能，明白TTL 门的开门电阻R ON ≥3K Ω时相当于在输入端得到高电平“1”，关门电阻R OFF ≤0.8K Ω时相当于在输入端得到低电平“0”。

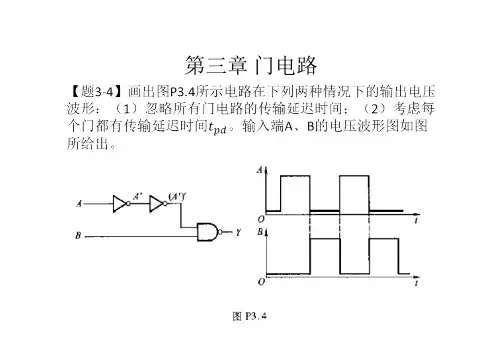
第三章门电路解：两种情况下的电压波形图如图A3.4所示。

【题3.7】试分析图3.7中各电路图的逻辑功能，写出输出的逻辑函数式。

（a ）图P3.7（a ）电路可划分为四个反相器电路和一个三输入端的与非门电路，如图所示。

从输入到输出逐级写出输出的逻辑函数式，'111'1'1'1)(,,,C B A D C C B B A A ''''111')(C B A C B A C B A D Y（b ）图P3.7（b ）电路可划分为五个反相器电路和一个或非门电路，如图所示。

从输入到输出逐级写出输出的逻辑函数式：'111''''()()YA B C A B C ABC（c ）图P3.7（c ）电路可划分为三个与非门电路、两个反相器电路和一个或非门电路，如图所示。

从输入到输出逐级写出输出的逻辑函数式：''')(,)(,)'(,)(G INHH EF G CD F AB E '''''()()'()'()()Y I H AB CD INH AB CD INH（d）图P3.7（d）电路可划分为两个反相器电路和两个传输门电路，如图所示。

从输入到输出逐级写出输出的逻辑函数式：'YBAAB'【题3.8】试画出图3-8（a）（b）两个电路的输出电压波形，输入电压波形如图（c）所示。

输出电压波形如右图所示：【题3.9】 在图3-21所示电路中，G 1和G 2是两个OD 输出结构的与非门74HC03，74HC03输出端MOS 管截止电流为 导通时允许的最大负载电流为这时对应的输出电压V OL （max ）=0.33V 。

负载门G 3-G 5是3输入端或非门74HC27，每个输入端的高电平输入电流最大值为 ，低电平输入电流最大值为 ，试求在 、、、、并且满足 ，的情况下， 的取值的允许范围。

数电课后标准答案康华光第五版（完整）第⼀章数字逻辑习题1．1数字电路与数字信号1.1.2 图形代表的⼆进制数0101101001．1．4⼀周期性数字波形如图题所⽰，试计算：（1）周期；（2）频率；（3）占空⽐例MSB LSB0 1 2 11 12 （ms）解：因为图题所⽰为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms 频率为周期的倒数，f=1/T=1/0.01s=100HZ占空⽐为⾼电平脉冲宽度与周期的百分⽐，q=1ms/10ms*100%=10%1.2数制2 1.2.2将下列⼗进制数转换为⼆进制数，⼋进制数和⼗六进制数（要求转换误差不⼤于4（2）127 （4）2.718解：（2）（127）D=72-1=（10000000）B-1=（1111111）B=（177）O=（7F）H（4）（2.718）D=(10.1011)B=(2.54)O=(2.B)H1.4⼆进制代码1.4.1将下列⼗进制数转换为8421BCD码：（1）43 （3）254.25解：（43）D=（01000011）BCD1.4.3试⽤⼗六进制写书下列字符繁荣ASCⅡ码的表⽰：P28（1）+ （2）@ （3）you (4)43解：⾸先查出每个字符所对应的⼆进制表⽰的ASCⅡ码，然后将⼆进制码转换为⼗六进制数表⽰。

（1）“+”的ASCⅡ码为0101011，则（00101011）B=（2B）H（2）@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的⼗六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的⼗六紧张数分别为34,331.6逻辑函数及其表⽰⽅法1.6.1在图题1. 6.1中，已知输⼊信号A，B`的波形，画出各门电路输出L的波形。

解: (a)为与⾮， (b)为同或⾮，即异或第⼆章逻辑代数习题解答2.1.1 ⽤真值表证明下列恒等式 (3)A B AB AB ⊕=+（A ⊕B ）=AB+AB 解：真值表如下A B A B ⊕ABAB A B ⊕AB +AB0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 11111由最右边2栏可知，A B ⊕与AB +AB 的真值表完全相同。

第一章 逻辑代数基础 例题1.与(10000111)BCD 相等的十进制数是87， 二进制数是1010111 十六进制数是57，2.AB+CD=0（约束项）求 的最简与或表达式。

解：D C A C B A Z +=，见图1-1， 得3.若F(A,B,C,D)=∑m(0,1,2,3,4,7,15）的函数可化简为： 则可能存在的约束项为（ 3 ）。

见图1-21．逻辑函数式Y A B C D =++（）的反演式为 D C B A + 2. 在下列不同进制的数中，数值最大的数是（ D ）1051A.（） .101010B 2（） 163E C.（） D.（01011001）8421BCD 码 3、用卡诺图化简下式为最简与或式。

D C B A ++ Y(A,B,C,D)= ∑m(0,2,4,5,6,8,9)+ ∑d(10,11,12,13,14,15) 4.已知F ABC CD =+选出下列可以肯定使F=0的情况（ D )A. A=0，BC=1B. B=C=1C. D=0，C=1D. BC=1，D=1 5、是8421BCD 码的是（ B ）。

A 、1010 B C 、1100 D 、11016、欲对全班43个学生以二进制代码编码表示，最少需要二进制码的位数是（ B ）。

A 、5B 、6C 、8D 、437、逻辑函数F(A,B,C) = AB+B C+C A 的最小项标准式为（ D ）。

A 、F(A,B,C)=∑m(0,2,4)B 、F(A,B,C)=∑m(1,5,6,7)C 、F(A,B,C)=∑m (0,2,3,4)D 、F(A,B,C)=∑m(3,4,6,7)Z A BC A B AC D =++Z Z AC AC =+()B C D C D ++1..2..3..4..AC A DA C AB A D A B A B B C++++8、用代数法化简下式为最简与或式。

A+CC B BC C B A BCD A A F ++++=判断题1.若两个函数具有不同的真值表，则两个逻辑函数必然不相等。

数电逻辑门电路逻辑门电路是数字电路中常见的一种电路结构，用于处理不同的逻辑运算和控制信号。

逻辑门电路通常由不同类型的逻辑门组成，如与门、或门、非门、异或门等。

在这篇文章中，我们将介绍几种常见的逻辑门电路以及它们的应用。

1. 与门电路与门电路是最基本的逻辑门之一，其功能是将两个输入信号进行逻辑与运算，输出结果为如果两个输入信号同时为高电平时输出高电平，否则输出低电平。

与门电路通常用于逻辑运算和控制信号的处理，比如电脑中的逻辑电路、开关控制等。

2. 或门电路或门电路是另一种常见的逻辑门，其功能是将两个输入信号进行逻辑或运算，输出结果为如果任一输入信号为高电平时输出高电平，否则输出低电平。

或门电路也广泛应用于逻辑运算和控制信号处理中，例如电脑中的逻辑电路、开关控制等。

3. 非门电路非门电路是一种单输入单输出的逻辑门，其功能是将输入信号取反输出，即如果输入信号为高电平则输出低电平，如果输入信号为低电平则输出高电平。

非门电路通常用于信号反转、逻辑反相等应用。

4. 异或门电路异或门电路是一种常见的逻辑门，其功能是将两个输入信号进行逻辑异或运算，输出结果为如果两个输入信号不相同则输出高电平，否则输出低电平。

异或门电路在数字电路设计中经常被使用，例如数据的误码检测、加法器电路等。

以上是几种常见的逻辑门电路，下面我们将介绍一个简单的逻辑门电路示例：4位全加器电路。

4位全加器电路是由4个异或门、3个与门和1个或门组成的逻辑电路，用于实现4位二进制数的加法运算。

该电路的原理是将两个4位二进制数相加，得到和输出以及进位输出。

当输入信号为A3-A0、B3-B0时，输出信号为S3-S0代表和值，C代表进位位。

在4位全加器电路中，每个异或门接收两个输入信号A和B，输出一个异或运算结果；每个与门接收三个输入信号A、B和C_in，输出一个与运算结果；一个或门接收四个输入信号S0-S3，输出一个或运算结果。

将这些逻辑门按照接线图正确连接，就可以实现全加器电路的功能。

逻辑门电路原理
逻辑门电路是由逻辑门元件（比如与门、或门、非门等）组成的电路，用于实现不同逻辑功能的处理。

逻辑门电路的原理是基于布尔代数的原理，通过输入信号的组合，产生特定的输出信号。

与门是逻辑门电路中最简单的一种。

它有两个输入端和一个输出端。

当两个输入同时为高电平（1）时，输出才为高电平（1），否则输出为低电平（0）。

与门电路可以用晶体管来实现。

其中，两个输入信号接通到两个晶体管的基极，输出信号从两个晶体管的发射极中获取。

或门是逻辑门电路中另一种常见的门电路。

它也有两个输入端和一个输出端。

当两个输入中至少一个为高电平（1）时，输出就为高电平（1），只有当两个输入都为低电平（0）时，输出为低电平（0）。

或门电路可以通过将两个输入信号连接到两个晶体管的集电极，输出从两个晶体管的发射极中获取来实现。

非门是逻辑门电路中最简单的一种反转门电路。

它只有一个输入端和一个输出端。

当输入为高电平（1）时，输出为低电平（0），反之亦然。

非门电路可以通过一个晶体管来实现，输入信号通过晶体管的基极，输出来自晶体管的发射极。

逻辑门电路的原理基于布尔代数，通过在输入信号之间的逻辑运算，实现特定的逻辑功能。

在电子数位系统中，逻辑门电路被广泛应用于数字电路中，如计算机、电子器件等。

它们可以
实现逻辑运算、信号控制、数据存储等功能，是现代电子设备中不可或缺的一部分。

数电逻辑门电路
逻辑门电路是数字电路中最基本的组成部分，它执行基本的逻辑运算，如 AND、OR、NOT 等。

常见的逻辑门
•AND 门：只有当所有输入都为高电平时，输出才为高电平。

•OR 门：只要有一个输入为高电平时，输出就为高电平。

•NOT 门：当输入为高电平时，输出为低电平，反之亦然。

•NAND 门：与 AND 门相同，但输出取反。

•NOR 门：与 OR 门相同，但输出取反。

•XOR 门：只有当输入不同时，输出才为高电平。

•XNOR 门：只有当输入相同时，输出才为高电平。

逻辑门符号
每个逻辑门都有一个标准符号，用于表示其功能和输入/输出关系。

逻辑门特性
•逻辑电平：逻辑门通常使用高电平和低电平表示二进制信号。

•传递延迟：逻辑门之间有延迟时间，称为传递延迟。

•扇出：逻辑门可以驱动多个其他逻辑门，其数量称为扇出。

•功耗：逻辑门消耗功率，这取决于其尺寸、类型和开关频率。

逻辑门应用
逻辑门电路用于各种数字系统中，包括：
•计算机
•智能手机
•数字仪表
•控制系统
•数据通信
逻辑门实现
逻辑门电路可以通过以下方式实现：
•分立器件：使用晶体管、电阻器和二极管等分立器件构建。

•集成电路（IC）：将多个逻辑门集成到一个单一的 IC 芯片中。

•现场可编程门阵列（FPGA）：提供可编程逻辑，允许用户配置自定义逻辑门电路。

数电组合逻辑电路门电路设计
数电组合逻辑电路的设计包括确定逻辑功能和选择适当的门电路进行实现。

首先，确定所需的逻辑功能。

这可能是一个布尔代数的表达式，如与、或、非等。

例如，如果需要实现一个逻辑与门，可以使用以下布尔代数表达式：Y = A * B。

然后，选择适当的门电路进行实现。

常见的门电路有与门、或门、非门等。

与门用于实现逻辑与功能，或门用于实现逻辑或功能，非门用于实现逻辑非功能。

对于上面的例子，可以选择一个与门电路进行实现。

与门电路有两个输入端和一个输出端。

根据布尔表达式，将输入A和
B连接到与门的两个输入端，将输出Y连接到与门的输出端。

最后，根据具体的设计需求，选择合适的门电路芯片进行设计。

常见的门电路芯片有与门芯片、或门芯片、非门芯片等。

可以根据需要的输入输出端口数目和电压要求选择合适的芯片。

综上所述，数电组合逻辑电路门电路设计包括确定逻辑功能、选择适当的门电路和门电路芯片进行实现。

什么是逻辑门电路逻辑门电路是指由逻辑门组成的电路，用于对逻辑信号进行运算和控制。

逻辑门是一种基本的数电器件，可以实现逻辑运算，如与、或、非等，常见的逻辑门有与门、或门、非门、异或门等。

逻辑门电路可以简单的理解为一个逻辑功能的实现器，根据输入信号的不同，输出不同的逻辑结果。

逻辑门使用布尔代数进行描述，通过将输入信号与逻辑运算规则相结合，得到输出信号。

目前，常见的逻辑门电路有数字式和模拟式两种。

数字式逻辑门电路主要用于数字计算机、数字电路和通讯等领域，其中包括与门、或门、与非门等。

模拟式逻辑门电路主要用于模拟计算机、模拟电路和通讯等领域，其中包括模拟与门、模拟或门等。

在数字电路中，逻辑门电路广泛应用于计算机的计算和控制系统中。

例如，在计算机的中央处理器（CPU）中，逻辑门电路用于处理和运算指令，控制计算机的各项操作。

此外，逻辑门电路还可以用于编码器、解码器、计数器、存储器等的设计与实现。

逻辑门电路的设计和实现需要经过多个步骤。

首先，需要确定所需的逻辑运算规则和功能；然后，选择合适的逻辑门类型和数量；接着，按照逻辑门的真值表，确定逻辑门的输入输出关系；最后，将逻辑门按照设计要求进行连接和布局。

在逻辑门电路的实现中，一般使用逻辑门芯片。

逻辑门芯片是将多个逻辑门组合在一个集成电路芯片中，使得电路更加简洁、稳定和可靠。

逻辑门芯片具有功能强大、体积小巧等特点，能够满足不同规模和需求的电路设计。

逻辑门电路的应用不仅仅局限于计算机领域，还广泛应用于电子、通信、自动控制、仪器仪表等领域。

逻辑门电路在现代技术中扮演着重要的角色，推动了数字化、自动化和智能化的发展。

总之，逻辑门电路是一种基本的数电器件，用于对逻辑信号进行运算和控制。

逻辑门电路广泛应用于计算机、电子、通信等领域，是现代技术发展的重要组成部分。

随着科技的进步，逻辑门电路的应用将会更加广泛，对推动技术的发展和应用有着重要的作用。