毕奥_萨伐尔定律的螺旋表达式

毕奥萨伐尔定律的数学表达式
毕奥萨伐尔定律是描述一个重要物理现象的重要定律。

1853年，德国物理学家威廉·毕奥萨·伐尔提出了这一定律，他指出，磁体周围存在一种旋转电流，磁体正在试图引导这种旋转电流。

由此，如果磁体不能无限循环这种电流，那么磁场强度就会减弱，直到磁体消失。

毕奥萨·伐尔定律的数学表达式是用来描述磁体的磁场的变化的重要理论，其定律如下：B⃗={μ⃗0 ·(I⃗·r̂)/4πr2}r̂, 其中B⃗是磁场，μ⃗0是真空磁导率，I⃗是电流，r̂是相对于磁片的单位向量。

从这个公式可以看出，磁场强度随着距离的增加而减弱，磁场强度和电流强度之间存在着内在联系。

毕奥萨·伐尔定律非常重要，它不仅在物理上解释了磁场的结构，而且是研究电磁相关问题的基础。

在电工学中广泛应用，例如在线圈的设计中，用伐尔定律可以迅速计算线圈的磁场，确定绕线的线圈，以及测量电压、电流和功率。

总之，毕奥萨·伐尔定律是一个重要及有效的定律，它可以解释磁体所受到的影响，而且它在电磁学中被广泛应用。

它的数学表达式让研究变得简单、快速，也显示出物理系统中物体与环境之间微妙的相互作用。

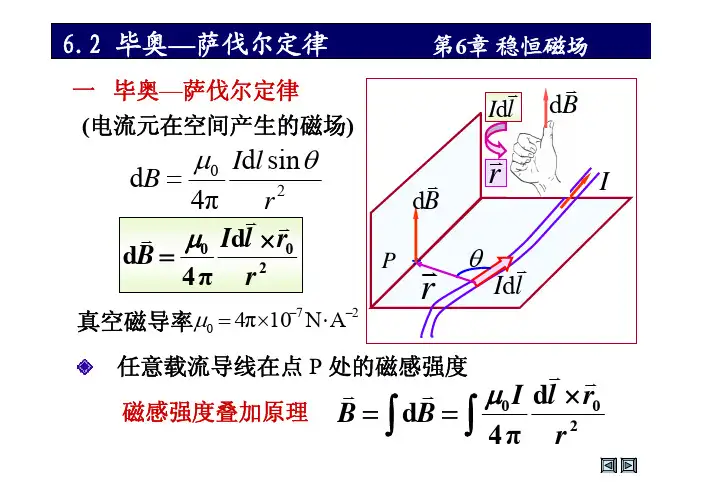
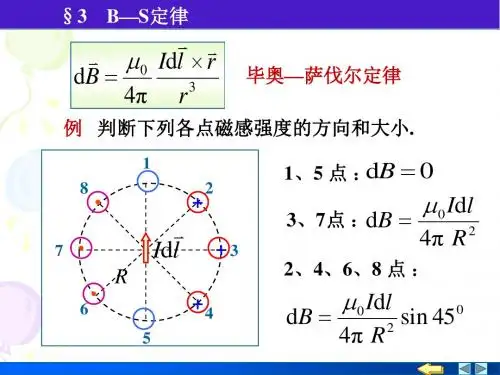
6.2 毕奥—萨伐尔定律一 毕奥—萨伐尔定律 (电流元在空间产生的磁场)第6章 稳恒磁场v Idlv dB4π r v v v μ0 Idl × r0 dB = 4π r2−7 −2 真空磁导率μ0 = 4π ×10 N ⋅ AdB =μ0 Idl sin θ2v dBP *v rθv IdlIv r任意载流导线在点 P 处的磁感强度 磁感强度叠加原理v v v v μ0 I dl × r0 B = ∫ dB = ∫ 2 4π r6.2 毕奥—萨伐尔定律v v v μ0 Idl × r0 毕奥—萨伐尔定律 dB = 2 4π r1 8第6章 稳恒磁场例 判断下列各点磁感强度的方向和大小.2dB = 0 1、5 点 ：3、7点 ：dB +3+7v IdlR6 5=μ 0 Id l4π R22、4、6、8 点 ：+4dB =μ 0 Idl4π R0 sin 45 26.2 毕奥—萨伐尔定律二 毕奥---萨伐尔定律应用举例第6章 稳恒磁场θ1、 θ2、 r0 例1 载流长直导线的磁场. 已知：真空中 I、zDθ2解dz θ vIzθ1rv dB* P yxor0dB = 2 4π r v dB 方向均沿r Ì任取电流元 Id z μ 0 Idz sin θ⊗Ì建立坐标系OXYCx 轴的负方向 μ0 Idz sinθ B = ∫ dB = ∫ 2 CD 4π r6.2 毕奥—萨伐尔定律Ì写出分量式第6章 稳恒磁场Idz sinθ B = ∫ dB = ∫ 2 CD 4π rÌ统一积分变量μ0zDθ2z = r0ctg(π −θ ) = −r0ctgθ ,dz θ vIzθ1rv dB* P yr = r0 / sinθxor0Cdz = r0dθ / sin θ μ 0 I sin θ dz B=∫ 2 4π r2=∫μ 0 sin 2 θ r0 d θ I sin θ 2 2 sin θ 4 π r06.2 毕奥—萨伐尔定律第6章 稳恒磁场B=μ0I4 π r0∫θθ21sin θ d θ =v B 的方向沿 x 轴的负方向.B=（cosθ1 − cosθ 2） 4π r0μ0 IzDθ2v B无限长载流长直导线的磁场.（cosθ1 − cosθ 2） 4π r0B=μ0 IIoxCθ1 → 0 θ2 →πμ0I2 π r0θ1P y+6.2 毕奥—萨伐尔定律无限长载流长直导线的磁场 I B第6章 稳恒磁场B=μ0I2π rIXB电流与磁感强度成右螺旋关系 半无限长载流长直导线的磁场π θ1 → 2 θ 2 →πBP =μ0I4π rIor* P6.2 毕奥—萨伐尔定律第6章 稳恒磁场例2 圆形载流导线的磁场. 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 求其轴线上一点 p 的磁感强度的方向和大小.v Idlrv Bv dBp *oRϕv BI 解 根据对称性分析4π r B = Bx = ∫ dB sin ϕdB =μ 0 Id l2x6.2 毕奥—萨伐尔定律 v IdlR第6章 稳恒磁场rxoϕr 2 2 2 ϕ r =R +x α μ 0 I cos α dl *p x B= 4 π ∫l r 2v dBcosα = R4π r μ 0 I cos αdl dB x = 2 4π rdB =μ 0 Id l2B=B=μ0 IR4π r 2 μ0 IR2 23 0∫2π Rdl3（ 2 x + R ）26.2 毕奥—萨伐尔定律第6章 稳恒磁场IR ox*v BxB=B=μ0 IR22 2 3讨 论（ 2 x + R ）2 v v 2）x < 0 B 的方向不变( I 和 B 成右螺旋关系） μ 0I B = 3）x = 0 2R 2 IR IS μ μ 0 0 4）x >> R ， B= B= 3 3 2x 2π x2 21）若线圈有 N 匝（ 2 x + R ）2 2 N μ 0 IR36.2 毕奥—萨伐尔定律 例：载流圆弧，已知 I , R , θ r 求： B 0 r r 解： B = ∫ dB r r μ 0 Idl sin( dl , r ) B = ∫ dB = 2 ∫ 4π R μ0 I Rθ μ0 Iθ = dl = 2 ∫ 4πR 0 4πR第6章 稳恒磁场 Iθ⊗ oR6.2 毕奥—萨伐尔定律(1） I （2 ） o+ （3） I R⊗第6章 稳恒磁场 （4）v R B x 0 μ0I o B0 = 2RI RBA =d （5） I *AR1• * oμ0 I4π d⊗B0 =μ0 I4RR2B0 =oμ0 I8RB0 =μ0 I4 R2−μ0 I4 R1−μ0 I4π R16.2 毕奥—萨伐尔定律(6)O•第6章 稳恒磁场B =IRμ0I8R•(7)R•OIμ0I + B = 4R 2π Rμ0I•(8)2π 3• OIRμ0I 3 (1 − B = + ) 6R 2π R 2⊗μ0I。

毕奥萨伐尔定律公式1埃尔维·毕奥萨伐尔定律埃尔维·毕奥萨伐尔定律（Erwin Bolza's Law）是一个定理，由德国数学家埃尔维·毕奥萨伐尔（Erwin Bolza）在1847年提出，指出把一个复数函数系统化为一个多项式来得到方程的解。

在这里，复数是表示多个自变量聚集在一起形成的函数，而多项式是一组关于自变量的有限阶多项式，当满足相应条件时，就可以将复数函数简化为多项式，从而得出所有的解决方案。

由于埃尔维·毕奥萨伐尔定律是一个常规的、可证明的定理，因此它被广泛应用于各种数学领域，包括几何、计算机科学和物理学等。

对于具有多个变量的函数系统，它可以比较快速地将复数函数简化为多项式，从而更容易求解。

2毕奥萨伐尔定理的原理埃尔维·毕奥萨伐尔定理的核心原理是，在满足一定条件的情况下，可以将一个复数函数简化为多项式，从而得出它的解。

首先，毕奥萨伐尔定理要求复数函数系统有@n@个自变量，其中每个自变量由特定的多项式表示，而这@n@个多项式的系数必须是一定的，唯一的属性是他们的阶数可以不同。

接下来，当@n@个多项式被联合起来时，它们就可以形成一个复数函数，其中也可以得到它们关于每个自变量的解。

但是，由于有许多系数参与到计算当中，这样的计算过程可能很耗时。

这时，埃尔维·毕奥萨伐尔定理的核心原理就起作用了：它可以把复数函数系统改写成一个多项式，这样就更容易求解，而@n@个多项式的系数也可以任意调整，以获得最优的解。

3应用由于埃尔维·毕奥萨伐尔定理对于多项式的变量以及联合变量的计算有重要的应用，因此它在多个领域中都有广泛应用。

例如，它可以用于求解一元二次方程组——一组有两个自变量的方程组——的解。

在这里，一元二次方程组有两个多项式，其中每个多项式有两个系数，这里也就是有两个自变量。

通过把它们简化成一个多项式，就可以求出来它们的解。

此外，埃尔维·毕奥萨伐尔定理还可以用于比较两个物体的动力学性质，因为它可以有效地求出这两个物体的总运动方程，以及这两个物体的动力学特性。

毕奥萨伐尔定律表达式
毕奥萨伐尔定律公式: k=107T·m·A-1。

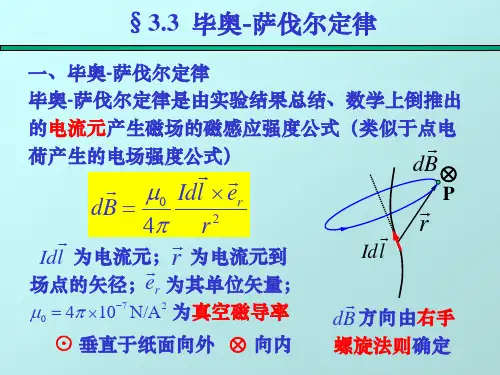
在静磁学中，毕奥－萨伐尔定律（英文：Biot-SavartLaw）描述电流元在空间任意点P处所激发的磁场。

具体表述如下：毕奥-萨伐尔公式，它指出，曲线涡丝段d l所诱导的速度d v，其方向垂直子d l和 r，大小则与距离 r的平方成反比，而且同d l和d l与 r
时夹角的正弦成正比。

毕奥萨伐尔定律介绍：
在恒定磁场中引入电流元的概念，分析电流元产生磁场的规律，即B-S定律，最后利用磁场的叠加原理，可以解决任意载流体所产生的稳恒磁场的分布。

B-S（毕奥萨伐尔定律）的物理意义：表明一切磁现象的根源是电流（运动电荷）产生的磁场。

反映了载流导线上任一电流元在空间任一点处产生磁感应强度在大小和方向上的关系。

由此定律原则上可以解决任何载流导体在其周围空间产生的磁场分别。

磁场，物理概念，是指传递实物间磁力作用的场。

磁场是一种看不见、摸不着的特殊物质。

磁场不是由原子或分子组成的，但磁场是客观存在的。

磁场具有波粒的辐射特性。

磁体周围存在磁场，磁体间的相互作用就是以磁场作为媒介的，所以两磁体不用在物理层面接触就能发生作用。