毕奥-萨伐尔定律实验

毕奥—萨伐尔定律1820年，毕奥和萨伐尔通过实验得到了载流导线周围磁场与电流的定量关系，拉普拉斯又以公式的形式概括得出电流元产生磁感强度d B 的规律。

为计算电流为I 的导线在空间某点户产生的磁感强度B ，设想将载流导线分割成许多电流元，用矢量dl I 表示．线元dl的方向与电流流向一致。

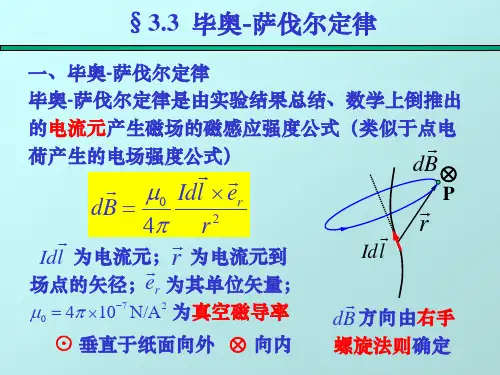
毕奥—萨伐尔定律指出：载流导线上的电流元dl I 在真空中某点P 的磁感度dB 的大小与电流元dl I 的大小成正比，与电流元dl I 和从电流元到P 点的位矢r 之间的夹角θ的正弦成正比，与位矢r 的大小的平方成反比，即20sin 4r dl I dB θπμ= （9-2a ） 上式中，πμ40为比例系数，0μ称为真空磁导率，其值为 270104--∙⨯=A N πμ dB 的方向垂直于dl I 和r 所确定的平面，当右手弯曲，四指从dl I 方向沿小于π角转向r 时，伸直的大姆指所指的方向为dB 的方向， 即dB 、dl I 、r 三个矢量的方向符合右手螺旋法则，如图9—2所示，因此，可将式(9—2a)写成矢量形式204r rdlI dB ⨯=πμ（9-2b）上式中，r0为位矢r的单位矢量．此即毕奥——萨伐尔定律的公式表述。

与点电荷的场强公式相似，毕奥——萨伐尔定律是求电流周围磁感强度的基本公式．磁感强度B也遵从叠加原理．因此，任一形状的载流导线在空间某一点P的磁感强度B，等于各电流元在该点所产生的磁感应强度dB的矢量和，即⎰⎰⨯==L r rIdldBB204πμ（9-3）例9-1例9-1求载流直导线周围的磁场。

解：设有长为L的直导线上通有电流I,求距离此导线为a处一点P的磁感应强度。

在直导线上任取一电流元Idl,它到P点的位矢为r,P点到直线的垂足为O，电流元到O的距离为l，Idl与r的夹角为θ，如左图所示。

根据毕萨定律可得该电流元在P点的磁感应强度dB的大小为20sin 4r l d I dB θπμ= dB 的方向垂直于纸面向里，图中用⊗表示.由于直导线上所有电流元在P 点的磁感应强度dB 的方向度相同,所以, P 点的磁感应强度B 的大小等于各电流元在P 点dB 的大小之和,即20sin 4r l d I B L θπμ⎰= 将上式中l 、r 、θ等变量统一为一个变量,以便积分.由图9-3所得()θπ-=ctg a lθθd adl 2sin =()θθπsin sin a a r =-=于是()2100c o s c o s 4s i n 421θθπμθθπμθθ-==⎰aI d a I B （9-4）式中,θ1和θ2分别为直导线两端的电流元与它到P 点的位矢之间的夹角。

毕奥-萨戈尔定律
毕奥-萨伐尔定律（英文：Biot-Savart Law）在静磁学中是描述电流元在空间任意点P处所激发的磁场。

毕奥-萨伐尔定律是法国科学家毕奥和萨伐尔合作研究发现的，以让-巴蒂斯特·毕奥（Jean-Baptiste Biot）和费利克斯·萨伐尔（Félix Savart）命名，1820年9月30日两人将第一个实验结果发表：载流长直导线到磁极距离与其作用力成反比，这一结果肯定了电和磁的联系。

毕奥-萨伐尔定律在静磁近似中是有效的，并且与安培（Ampère）的电路规律和磁性高斯定律一致。

毕奥-萨伐尔定律文字描述：电流元Idl在空间某点P处产生的磁感应强度dB的大小与电流元Idl的大小成正比，与电流元Idl所在处到P点的位置矢量和电流元Idl之间的夹角的正弦成正比，而与电流元Idl到P点的距离的平方成反比。

毕奥-萨伐尔定律在生产和生活中的应用有磁悬浮列车、根据工件大小来选择充磁电流的大小，从而达到磁粉探伤所需的磁场等。

毕奥-萨伐尔定律验证实验实验目的1. 测定直导体和圆形导体环路激发的磁感应强度与导体电流的关系2. 测定直导体激发的磁感应强度与距导体轴线距离的关系3. 测定圆形导体环路激发的磁感应强度与环路半径以及距环路距离的关系实验原理根据毕奥-萨伐尔定律，电流元在I d l 空间某点r 处产生磁感应强度d B 的大小：与I d l 的大小成正比，与电流元到该点的距离r 的平方成反比，与I d l 和r 之间小于π的夹角α的正弦成正比，比例系数为πμ4/0，即 02d sin d 4I l B rμαπ=（1） 式中0μ称为真空磁导率，其值为A /m T 10470⋅⨯=-πμ。

d B 的方向垂直于I d l 与r 构成的平面，用右手螺旋法则确定。

毕奥-萨伐尔定律的矢量表达式为 02d d 4rI rμπ⨯=l e B （2） 式中e r 是r 方向上的单位矢量。

对于确定几何形状的导体，利用公式（1）对d B 积分，就得到该载流导体产生的总磁感应强度B 。

例如：一根无限长导体，在距轴线r 的位置产生的磁场大小为：002IB r μπ=（3） 而半径为R 的圆形导体回路在圆环轴线上距圆心x 处产生的磁场大小为：()22003232222IR IR B r R xμμ==+ （4）本实验中，将分别利用轴向以及切向磁感应强度探测器来测量上述导体产生的磁场。

实验仪器：毕-萨实验仪，探头（黑点朝上），电流源，待测圆环（其半径分别为20mm 、40mm 、60mm ），待测直导线，槽式导轨及支架。

实验步骤： 一、 直导体激发的磁场1. 将直导线插入支座上；2. 将恒流源上红、黑两导线对应接到直导体两端；3. 将磁感应强度探测器与毕-萨实验仪连接，方向切换为垂直方向，并调零；4. 将磁感应强度探测器与直导体中心对准；5. 开始时使带电直导线和探测器在同一平面内，相互接触且互相垂直，此时可以近似认为距离0cm x =； 6. 打开恒流源电源。

毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。

微分形式为：整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。

磁感应线的方向服从右手定则，如图。

二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布：载流直导线；圆电流。

例1.载流长直导线的磁场解：建立如图坐标系，在载流直导线上，任取一电流元Idz，由毕-萨定律得元电流在P点产生的磁感应强度大小为：方向为垂直进入纸面。

所有电流元在P点产生的磁场方向相同，所以求总磁感强度的积分为标量积分，即：（1）由图得：,即：此外：，代入（1）可得：讨论：（1）无限长直通电导线的磁场：（2）半无限长直通电导线的磁场：（3）其他例子例2:圆形载流导线轴线上的磁场：设在真空中，有一半径为 R ，通电流为 I 的细导线圆环，求其轴线上距圆心 O 为 x 处的P点的磁感应强度。

解：建立坐标系如图，任取电流元，由毕-萨定律得：，方向如图：，所有dB形成锥面。

将dB进行正交分解：，则由由对称性分析得：，所以有:，因为： ,r=常量，所以：，又因为：所以：，方向：沿x轴正方向，与电流成右螺旋关系。

讨论：（1）圆心处的磁场：x=0 ，。

（2）当即P点远离圆环电流时，P点的磁感应强度为：。

例3：设有一密绕直螺线管。

半径为 R ，通电流 I。

总长度L，总匝数N（单位长度绕有n 匝线圈），试求管内部轴线上一点 P 处的磁感应强度。

解：建立坐标系，在距P 点 x 处任意截取一小段 dx ，其线圈匝数为: 电流为：。

其相当于一个圆电流，它在P点的磁感应强度为：。

因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右，所以整个螺线管在P点的磁感应强度的大小为：因为：代入上式得：所以：讨论：（1）管内轴线上中点的磁场:（2）当 L>>R时，为无限长螺线管。

此时,，管内磁场。

即无限长螺线管轴线上及内部为均匀磁场，方向与轴线平行满足右手定则。

毕奥萨伐尔定律实验报告本次实验旨在验证毕奥萨伐尔定律，通过对于电流和磁场的测量，利用毕奥萨伐尔定律的公式计算出两者之间的关系。

实验结果表明，电流和磁场之间确实存在一定的关系，验证了毕奥萨伐尔定律的正确性。

关键词：毕奥萨伐尔定律；电流；磁场；实验引言：毕奥萨伐尔定律是描述电流和磁场相互作用的基本定律，它揭示了电流和磁场之间的密切关系。

在现代物理学中，毕奥萨伐尔定律是一个非常重要的定律，它被广泛应用于电磁学、电动力学、电子学、通信等领域。

因此，本次实验旨在验证毕奥萨伐尔定律的正确性，通过实验数据的收集和分析，得出电流和磁场之间的关系，为后续的研究提供实验基础。

实验材料和方法：材料：导线、电池、磁铁、万用表、磁力计、直尺。

方法：1.将导线固定在直尺上，使其与直尺成为一条直线。

2.将电池连接到导线两端，使电流通过导线。

3.将磁铁放置在导线附近，测量磁场强度。

4.在不同的电流强度下，重复步骤3，记录磁场强度。

5.通过毕奥萨伐尔定律的公式计算出电流和磁场之间的关系。

实验结果分析：在本次实验中，我们测量了不同电流强度下的磁场强度，并记录了实验数据。

通过毕奥萨伐尔定律的公式计算出电流和磁场之间的关系，得到了如下图所示的实验结果：图1 电流和磁场之间的关系曲线从图1可以看出，电流和磁场之间确实存在一定的关系，随着电流的增大，磁场强度也随之增大。

这与毕奥萨伐尔定律的预测是一致的，验证了毕奥萨伐尔定律的正确性。

结论：通过本次实验，我们成功地验证了毕奥萨伐尔定律的正确性，证明了电流和磁场之间确实存在一定的关系。

这对于后续的研究和应用具有重要的意义。

同时，我们也应该注意到实验中存在的误差，尽可能地减小误差对实验结果的影响，提高实验的准确性。