金属线胀系数的测定--南昌大学-物理实验

实验四 利用直读式测量仪测定金属的线胀系数【实验目的】利用直读式测量仪测量金属棒的线胀系数； 【实验仪器】DH4608金属热膨胀系数试验仪、不锈钢管、钢卷尺 【实验原理】已知金属的线胀方程为：)1(0t l l α+=，其中0l 是金属在00C 时的长度。

当温度为1t 时，)1(10t l l α+=当温度为2t 时，设金属棒伸长量为l ∆，则有：)1(20t l l l α+=∆+ 两式相减得：t l t t l l ∆⋅=-=∆αα0120)(，其中α为金属的线胀系数。

实验时，利用DH4608金属热膨胀系数试验仪，每5℃设定一个控温点，利用热电偶记录样品上的实测温度和千分尺上的变化值。

根据数据l ∆和t ∆，画出l ∆（作y 轴）－t ∆（作x 轴）的曲线图，观察其线型性，并利用图形求出斜率，计算样品（不锈钢管）的线胀系数。

【实验步骤】1、将试验样品（不锈钢管）固定在实验架上，注意挡板要正对千分尺；2、调节千分尺和挡板的位置，保证两者无间隙且千分尺有足够的伸长空间；3、打开电源和水泵开关，每5℃设定一个控温点，记录样品的实测温度和千分尺上的变化值。

实际操作时，由于千分尺的指针在不停地转动，所以在设定的控温点不易准确读数，从而导致样品加热后的伸长量测量不准确。

具体操作可改为：在加热过程中，当观察到千分尺的指针转动匀速时，在千分尺上设定一个记录起点（比如0格），记下此时的温度值和数字电压表上的示值作为第一组实验数据。

以后每当千分尺的指针转过50格（或30格）记录一组温度值和数字电压表上的示值，填入设计的记录表中。

实验结束后再根据铜—康铜热电偶分度表将数字电压表上的示值转换为温度值作为试验样品的实际温度。

4、根据数据l ∆和t ∆，画出l ∆（作y 轴）－t ∆（作x 轴）的曲线图，观察其线型性。

5、利用图形求出斜率，计算样品的线胀系数（0l k =α，k 为斜率，0l 近似为室温下金属棒的有效长度）。

金属线胀系数的测定实验目的：1）学会用千分表法测量金属杆长度的微小变化2）测量金属杆的线胀系数，并判断此金属为何种金属实验仪器：实验原理：大家都知道热胀冷缩的现象，一般固体的长度或体积会随着温度的升高而膨胀，这就是固体的热膨胀。

设物体的温度改变Δt 时，其长度改变量为ΔL,如果Δt 足够小，则Δt 与ΔL 成正比，并且也与物体的原长有关系。

因此它们三个量之间有：ΔL=αL Δt式中的比例系数α称为固体的线胀系数，其物理意义是温度每升高1℃时其伸长量与它在0℃时长度的比。

设金属在0℃时的长度是L0,当温度升高为t ℃时其长度为Lt,则有：（Lt-L0)/L0=αt 即Lt=L0(1+αt)如果金属杆在温度为t1,t2时的长度分别为L1，L2，则可加热箱恒温控制仪以得到：L1=L0(1+αt1),L2=L0(1+αt2)因为L1，L2非常接近，所以得到下式：α=（L2-L1)/L0(t2-t1)由上式测得L1，L2，t1,t2就可以测得α值了。

实验过程： 1）接好电源和各个接口。

2）打开恒温控制仪，记录室温t1,再设定温度最大值，再记录此时千分表读数n1，最后按下确定键开始加热。

（实验所用金属杆0℃时长度为400mm)3）每隔5℃读一次数tn ，同时记录千分表读数n n 。

4) 将数据整理填入设计好的表格中，待处理。

实验数据记录与处理： t1=21℃L0=400mm n1=0.4012mm tn/℃ 26 3136 41 46 51 tn-t1/℃ 510 15 20 25 30 nn /mm 0.4630 0.5119 0.553 0.591 0.624 0.658 nn -n1/mm 0.062 0.111 0.152 0.19 0.223 0.26以nn-n1为横坐标，tn-t1为纵坐标作出曲线：由关系式可得直线的斜率即为：αL0,通过直线先求出斜率k 的大小，再计算α的值得α=1.975*e-5以上是通过作图法求斜率计算线胀系数α，下面通过逐差法 求线胀系数： 计数次数 12 3 4 5 ni 0.4012 0.46300.5119 0.5530 0.5912 计数次数 3 45 6 7 n(i+2) 0.5119 0.55300.5912 0.6240 0.6582 Δn 0.1107 0.09 0.0793 0.071 0.0675n n ∑∆=∆代入数据得n ∆=0.0836mm 。

金属线膨胀系数的测定实验报告一、实验目的。

本实验旨在通过测定金属线的膨胀系数，探究金属在受热作用下的膨胀规律，并验证线性膨胀系数的概念。

二、实验原理。

金属在受热作用下会发生线性膨胀，其膨胀量与温度变化呈线性关系。

金属线的膨胀量可用以下公式表示：ΔL = αL0ΔT。

其中，ΔL为金属线的膨胀量，α为线性膨胀系数，L0为金属线的原始长度，ΔT为温度变化量。

三、实验器材。

1. 金属线。

2. 热水槽。

3. 温度计。

4. 尺子。

四、实验步骤。

1. 准备金属线，并测量其原始长度L0。

2. 将金属线固定在支架上。

3. 将热水倒入热水槽中，待温度稳定后，记录水温作为初始温度T1。

4. 将金属线放入热水中，测量金属线的膨胀量ΔL。

5. 记录金属线在热水中的最终温度T2。

6. 根据实验数据计算金属线的线性膨胀系数α。

五、实验数据记录。

1. 金属线原始长度L0 = 1m。

2. 初始温度T1 = 25°C。

3. 最终温度T2 = 75°C。

4. 金属线膨胀量ΔL = 5mm。

六、实验结果分析。

根据实验数据计算得到金属线的线性膨胀系数α为：α = ΔL / (L0ΔT) = 5mm / (1m × 50°C) = 1 × 10^-4 /°C。

七、实验结论。

通过本实验的测定和计算，验证了金属线在受热作用下会发生线性膨胀的规律，并得到了金属线的线性膨胀系数α。

实验结果表明，金属线的膨胀量与温度变化呈线性关系，膨胀系数是一个常数，可用于预测金属在不同温度下的膨胀量。

八、实验注意事项。

1. 在实验过程中要小心热水的温度，避免烫伤。

2. 测量金属线的膨胀量时要注意准确度，避免误差。

九、实验总结。

本实验通过测定金属线的膨胀量，验证了金属在受热作用下的线性膨胀规律，得到了金属线的线性膨胀系数α。

实验结果对于理解金属膨胀规律具有重要意义，也为工程应用提供了重要参考。

以上为金属线膨胀系数的测定实验报告。

金属线胀系数的测定实验报告
本实验旨在测定金属线的线胀系数，了解金属线的热膨胀特性。

实验原理：
金属线热膨胀的原理是，当金属受热时，其分子内部的热运动增强，分子之间的距离也随之增大，从而导致物体的尺寸扩大，即产生热膨胀现象。

金属线的线胀系数是指在单位温度变化下，金属线长度增加的比例。

实验器材：
1.金属线
2.测温仪
3.皮尺
4.温度计
5.实验台
实验步骤：
1.将金属线固定在实验台上，用皮尺测出金属线的长度。

2.将测温仪夹在金属线上，并将温度计插入测温仪中，记录下此时的温度。

3.将热水放入容器中，在温度计显示为100℃时，测量金属线的长度，并记录下此时的温度。

4.根据所得数据计算出金属线的线胀系数。

实验结果：
测得金属线初始长度为10cm，温度为20℃；在100℃下，金属
线长度为10.5cm。

根据公式：线胀系数=（ΔL/L）/ΔT
其中，ΔL为金属线的长度变化量，ΔT为温度变化量。

则可得出线胀系数为：（0.5/10）/（100-20）=0.00025/℃
实验结论：
通过实验得出金属线的线胀系数为0.00025/℃。

这说明在一定温度范围内，金属线的长度会随温度的升高而增大，具有热膨胀的特性。

掌握金属线的线胀系数能够为工程设计提供重要的参考依据，特别是在高温环境下工作的机器和设备的设计中更为重要。

金属线胀系数的测定实验报告金属线胀系数的测定实验报告引言：金属的热胀冷缩性质是物理学中的一个重要研究领域。

金属的线胀系数是描述金属在温度变化时长度变化的物理量。

本实验旨在通过测定不同金属的线胀系数，探究金属的热胀冷缩规律。

实验装置与方法：实验装置包括一个恒温槽、一根金属线、一个测微器和一个温度计。

首先，将金属线固定在两个支架上，保证其自由伸缩。

然后，将恒温槽中的温度调至适当的初始温度，测量金属线的初始长度。

接下来，将恒温槽中的温度逐渐升高，并记录每个温度下金属线的长度变化。

同时，使用温度计测量恒温槽中的温度。

实验结果与分析：我们选取了铜、铁和铝作为实验材料，进行了线胀系数的测定。

下表列出了实验数据：温度（℃）铜线长度（cm）铁线长度（cm）铝线长度（cm）20 10.0 10.0 10.030 10.2 10.1 10.140 10.4 10.2 10.250 10.6 10.3 10.360 10.8 10.4 10.4根据实验数据，我们可以计算出每个金属的线胀系数。

线胀系数的计算公式为：线胀系数= (ΔL / L0) / ΔT其中，ΔL为长度变化，L0为初始长度，ΔT为温度变化。

以铜为例，当温度从20℃升至30℃时，长度变化为0.2cm。

初始长度为10.0cm，温度变化为10℃。

代入公式计算得到铜的线胀系数为：线胀系数 = (0.2 / 10.0) / 10 = 0.002同样的方法可以计算出铁和铝的线胀系数。

铁的线胀系数为0.001，铝的线胀系数为0.0015。

通过比较不同金属的线胀系数，我们可以发现铝的线胀系数最大，铜次之，铁最小。

这是因为金属的线胀系数与其晶格结构和原子间的结合力有关。

铝的晶格结构较松散，原子间的结合力较弱，因此其线胀系数较大。

铜的晶格结构较紧密，原子间的结合力较强，因此其线胀系数较小。

铁的晶格结构介于铝和铜之间，因此其线胀系数处于中间水平。

结论：通过本实验，我们成功测定了铜、铁和铝的线胀系数，并比较了它们之间的差异。

金属线胀系数的测定实验报告资料实验报告：一、实验目的通过实验掌握金属线的胀系数的测定方法，了解线性膨胀系数的概念，掌握测量金属线胀系数的步骤和注意事项。

二、实验原理当一条金属线受热后，由于温度的升高导致其长度发生了改变，这种现象被称为热膨胀。

线性膨胀系数α是指物体在温度每变化1℃时，单位长度发生的变化量。

金属线胀系数的测定方法是采用差极式法。

实验中选用圆形金属丝，其胀系数可以用弹簧测微计来测量。

三、实验步骤1.将样品金属线固定在实验架上，线的一端用两片木板固定，另一端通过夹具固定在弹簧测微计的下端。

2.设定弹簧测微计的初始读数，并记录下来。

3.将电热器连接电源，并设置恒温水槽温度。

4.待水温稳定后，在恒温水槽中浸泡金属线，并等待其达到恒定温度。

6.将采样点数据整理，计算金属线的胀系数。

四、实验数据实验数据如下表所示：温度（℃）弹簧测微计读数（mm）膨胀量ΔL（mm）20 124.5 040 125.0 0.560 125.5 1.080 126.0 1.5100 126.5 2.0由上表可知，金属线在温度上升到100℃时，长度发生了2.0mm的变化。

根据线性膨胀系数的公式：ΔL = L × α × ΔT其中ΔL为长度变化量，L为材料长度，α为线性膨胀系数，ΔT为温度变化量。

可以得到公式：根据实验数据计算得到金属线的胀系数为：α = 2.0 ÷ 500 ÷ 80 = 0.00005 ℃-1五、实验结论通过差极式法测量，本实验测得圆形金属丝的胀系数为0.00005 ℃-1。

六、实验注意事项1. 金属线需保持一定的拉力，以保证数据结果的准确度。

2. 弹簧测微计需经常校准，以确保其读数的准确度。

3. 采样点的选取应尽量均匀，以得到更为准确的结果。

4. 实验前需检查实验设备的安全性，保证实验过程的安全。

实验四 金属线胀系数的测定【实验目的】学习用光杠杆法测量金属棒的线胀系数。

【实验仪器】GXZ 型金属系数测定仪，光杠杆，尺度望远镜，钢卷尺，游标卡尺，蒸汽发生器，待测金属棒。

【实验原理】固体的长度通常随着温度的升高而增加，其长度l 和温度t 之间的关系为)1(20 +++=t t l l βα (4-1)式中0l 为温度C t 00=的长度，α、β是和被测物体有关的常数，都为很小的数值，而β以下各系数与α相比更小，常温下可以忽略，则(13-1)可写成)1(0t l l α+= (4-2)式子中α即为通常所称的线胀系数，单位是10-C 。

设物体在温度为C t 01时的长度为l ，温度升高到C t 02时，其长度增加δ，根据式(13-2)，可得)1(10t l l α+=)1(20t l l αδ+=+由此二式消去0l ，整理后得出)34()(112---=t t t l δδα因l 与δ相比很小，112)(t t t l δ>>-，所以式(13-3)可近似写成)44()(12--=t t l δα线胀系数α测量中，最重要的工作是如何准确测量出当温度变化时引起的金属长度产生的微小变化δ。

实际测量中常常使用的方法有：（1）光杠杆法测量微小长度变化法实验时将待测金属棒直立在金属线胀系数测定仪的金属筒中(图13-1)，将光杠杆的后足尖置于金属棒的上端，二前足置于固定台上。

设在温度C t 01时，通过望远镜和光杠杆平面镜，看见直尺上的刻度1a 刚好在望远镜中叉丝横线(或交点)处，当温度升高至C t 02时，直尺上刻度2a 移至叉丝横线上，根据光杠杆原理(光杠杆的使用方法参见本书实验九中的仪器原理介绍)可得)54(2)(12--=Dda a δ式中d 为光杠杆后足尖到二前足尖连线的垂直距离，D 为光杠杆镜面到直尺的距离。

将式(13-5)代入式(13-4)中，则)64()(2)(1212---=t t Dl da a α(2)利用螺旋测微器原理测量金属微小长度 如图13-2所示。

金属线胀系数的测量实验报告一、实验目的1、学会使用千分表测量金属杆的微小长度变化。

2、掌握用光杠杆法测量金属线胀系数的原理和方法。

3、加深对热膨胀现象的理解，培养实验操作和数据处理能力。

二、实验原理当固体温度升高时，由于分子的热运动加剧，固体的长度会发生微小的增加。

这种现象称为线膨胀。

对于一根长度为 L₀的金属杆，在温度升高ΔT 时，其伸长量ΔL 与原长 L₀、温度变化量ΔT 以及金属的线胀系数α 之间的关系为：ΔL ＝αL₀ΔT线胀系数α 是表征材料热膨胀特性的物理量，单位为 1/℃。

本实验采用光杠杆法测量金属杆的微小伸长量。

光杠杆是一个带有可旋转平面镜的三脚支架，其原理是利用光的反射将微小长度变化进行放大。

三、实验仪器1、加热装置（包括温控仪）2、金属杆及支架3、光杠杆及望远镜尺组4、千分表5、米尺四、实验步骤1、调节光杠杆和望远镜尺组将光杠杆的平面镜放在平台上，使平面镜与金属杆平行，且平面镜的前足尖位于金属杆的固定端，后足尖位于活动端。

调整望远镜尺组，使其与光杠杆平面镜等高，且望远镜的光轴与平面镜垂直。

通过望远镜能清晰地看到标尺的像。

2、测量金属杆的初始长度 L₀用米尺测量金属杆在室温下的长度，测量多次取平均值。

3、安装千分表将千分表安装在金属杆的活动端，使其测量杆与金属杆垂直，并预压一定的量，记录千分表的初始读数。

4、开始加热并测量打开加热装置，设置合适的升温速率和目标温度。

每隔一定的温度间隔，读取千分表和望远镜中标尺的读数。

5、数据记录将测量得到的温度、千分表读数和望远镜标尺读数记录在表格中。

五、数据处理1、计算金属杆的伸长量根据千分表的读数变化计算金属杆的微小伸长量ΔL₁。

利用光杠杆原理，通过望远镜标尺读数的变化计算金属杆的伸长量ΔL₂。

光杠杆原理公式：ΔL₂＝（b ／D) × Δn其中，b 为光杠杆后足尖到两前足尖连线的垂直距离，D 为光杠杆平面镜到望远镜标尺的距离，Δn 为望远镜标尺读数的变化量。

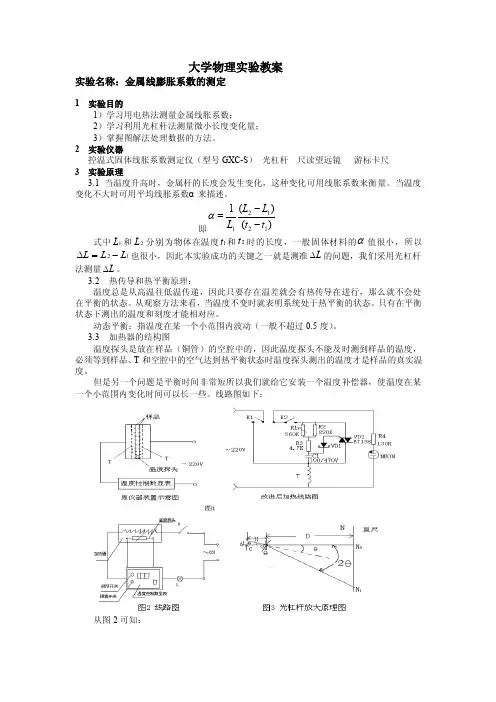
大学物理实验教案实验名称：金属线膨胀系数的测定1 实验目的1）学习用电热法测量金属线胀系数；2）学习利用光杠杆法测量微小长度变化量；3）掌握图解法处理数据的方法。

2 实验仪器控温式固体线胀系数测定仪（型号GXC-S ） 光杠杆 尺读望远镜 游标卡尺 3 实验原理3.1 当温度升高时，金属杆的长度会发生变化，这种变化可用线胀系数来衡量。

当温度变化不大时可用平均线胀系数α来描述。

即)()(112121t t L L L --=α式中1L 和2L 分别为物体在温度1t 和2t 时的长度，一般固体材料的α值很小，所以12L L L -=∆也很小，因此本实验成功的关键之一就是测准L ∆的问题，我们采用光杠杆法测量L ∆。

3.2 热传导和热平衡原理：温度总是从高温往低温传递，因此只要存在温差就会有热传导在进行，那么就不会处在平衡的状态。

从观察方法来看，当温度不变时就表明系统处于热平衡的状态。

只有在平衡状态下测出的温度和刻度才能相对应。

动态平衡：指温度在某一个小范围内波动（一般不超过0.5度）。

3.3 加热器的结构图温度探头是放在样品（铜管）的空腔中的，因此温度探头不能及时测到样品的温度，必须等到样品、T 和空腔中的空气达到热平衡状态时温度探头测出的温度才是样品的真实温度。

但是另一个问题是平衡时间非常短所以我们就给它安装一个温度补偿器，使温度在某一个小范围内变化时间可以长一些。

线路图如下：从图2可知：()D NH D H L 2201∆=N -N =∆所以可得：()1221t t D L -H ∆N =α=t LD ∆H∆N 2 4 教学内容1）用卷尺测量金属杆的长度L2）光杠杆放在仪器平台上，其后足尖放在金属杆顶端的金属套上，光杠杆的镜面在铅直方向。

在光杠杆前1.5~2.0m 处放置望远镜及直尺（尺在铅直方向）。

调节镜尺组让望远镜与直尺相对镜面成对称关系，调节望远镜的目镜使叉丝清晰，如图2，再调节望远镜使直尺的象进入望远镜中。

金属线胀系数的测定实验数据实验目的:测定金属的线胀系数，了解线胀系数的测量方法及实验结果的处理方法。

实验原理:金属的线胀系数是指金属在温度变化时，长度和直径发生变化的大小。

在进行线胀系数测定时，需要将金属样品在两个温度下测量其长度和直径，然后计算出其线胀系数。

通常情况下，线胀系数可以通过公式 C=([L-L0]/L0)×100% 来计算，其中 C 为线胀系数，[L-L0] 为温度变化时金属的长度变化，L0 为金属在恒温下的长度。

实验步骤:1. 准备试样：从不同部位取出长度约为 100mm 的金属样品，将其固定在拉伸机上。

2. 测量起始长度和直径：在室温下测量金属样品的长度和直径，并记录下来。

3. 将金属样品恒温至目标温度：将金属样品放置在恒温箱中，使其恒温至目标温度。

常用的目标温度范围为室温至 300°C。

4. 测量结束长度和直径：在目标温度下，再次测量金属样品的长度和直径，并记录下来。

5. 计算线胀系数：根据实验数据和公式 C=([L-L0]/L0)×100% 计算金属的线胀系数。

实验数据:表格 1:金属的线胀系数测量数据| 温度 (°C)| 长度变化 (%) | 直径变化 (%) | 线胀系数 | | -------- | -------- | -------- | -------- || 20 | -3.8 | -2.1 | 0.16 || 50 | -10.3 | -6.2 | 0.21 || 100 | -21.8 | -12.9 | 0.26 || 150 | -32.3 | -20.6 | 0.31 || 200 | -41.7 | -28.9 | 0.36 |实验结果分析:从表格 1 中可以看出，金属的线胀系数随着温度的升高而减小。

在室温下，金属的线胀系数通常在 0.17 左右。

在目标温度下，金属的线胀系数通常会比室温下的线胀系数小，这是因为在高温下金属的原子运动更加剧烈，导致金属的线胀系数减小。

实验 4.20 金属线膨胀系数的测定【实验目的】1．理解线膨胀系数的意义，掌握测定金属杆线膨胀系数的方法。

2．掌握用光杠杆测量固体微小伸长量的原理及方法。

【实验仪器】金属线胀系数测定仪、光杠杆、米尺、望远镜、游标卡尺、电子温度计。

【实验原理】一、线胀系数测量的基本原理任何物体都具有“热胀冷缩”的特性，这个特性在工程设计、精密仪表设计、材料的焊接和加工中都必须加以考虑。

线胀系数是描述材科受热膨胀的一项重要参数，金属线胀系数的测定是大学物理实验中一个重要的热学实验。

测量金属线胀系数的方法按加热方式分为流水加热法、水蒸气加热法、电加热法等；按测量方式分为：千分表法、组合法、单色光的劈尖干涉法、光杠杆法、传感器测量法等。

目前，金属线胀系数测量较为常见的是利用电加热待测金属杆，采用温度计在多个温度工作点下，用尺度望远镜和光扛杆测量金属杆由不同状态温差所引起的长度变化，从而得到金属杆的线胀系数。

固体加热时，体积将增大，这是一般物体所具有“热胀冷缩”的特性，固体受热后长度的增长称为“线膨胀”，其长度L和温度之间的关系为L=L0(1+αt+βt2+⋯) (4.20.1）式中L0为温度 t=0℃时的长度。

α、β……是和被测物质有关的常数，都是很小的数值。

而β以后各系数和α相比更小。

所以在常温下可以忽略，则（4.20.1）式可写成：L=L0(1+αt)（4.20.2）式中α就是通常所称的线胀系数，其物理意义为温度每升1℃度时物体的伸长量与它在零度时的长度比，单位是℃-1。

如果在温度 t1和t2时，金属杆的长度分别为L1和 L2则可写出：L1=L0(1+αt1)（4.20.3）L2=L0(1+αt2)（4.20.4）将式（4.20.3）代入式（4.20.4），化简后得：α=L2−L1L1(t2−L2L1t1)（4.20.5）由于 L2与L1变化微小，L2L1⁄≈1所以（4.20.5）式可近似写成α=L2−L1L1(t2−t1)=∆LL1∆t（4.20.6）其中∆L 是温度由t1升至t2时金属棒的伸长量。

金属线胀系数的测定实验报告数据一、实验目的1、学会使用千分表测量微小长度的变化。

2、掌握用光杠杆法测量金属棒的线胀系数。

3、了解金属受热膨胀的规律。

二、实验原理固体受热时会发生膨胀，其长度的增加量与温度的升高量成正比。

设固体在温度为 t₁时的长度为 L₁，温度升高到 t₂时的长度为 L₂，线胀系数为α，则有：ΔL ＝ L₂ L₁＝αL₁Δtα ＝（L₂ L₁) ／（L₁Δt)由于金属棒的伸长量ΔL 很小，难以直接测量，本实验采用光杠杆法进行测量。

光杠杆原理：光杠杆是一个带有三个尖足的平面镜，前两尖足放在一个固定的平台上，后尖足放在待测金属棒的顶端。

当金属棒受热伸长时，光杠杆的后尖足会随之上升，从而带动平面镜转动一个微小的角度θ。

通过望远镜和标尺，可以测量出平面镜转动角度θ所对应的标尺读数的变化量 n。

根据几何关系，有：ΔL ＝ b·n ／ 2D其中，b 为光杠杆常数（即前两尖足间的距离），D 为望远镜到平面镜的距离。

将上式代入线胀系数的表达式，可得：α ＝（b·n) ／（2D·L₁Δt)三、实验仪器1、加热装置：包括电炉、石棉网等。

2、金属棒：待测金属材料制成。

3、光杠杆及望远镜、标尺。

4、千分表。

5、温度计。

四、实验步骤1、调整光杠杆和望远镜的位置，使望远镜中能够清晰地看到标尺的像。

2、测量光杠杆常数 b 和望远镜到平面镜的距离 D。

3、用千分表测量金属棒在室温 t₁时的长度 L₁，并记录。

4、接通电炉电源，对金属棒进行加热，同时观察温度计的示数。

每隔一定温度间隔，记录一次标尺的读数 n 和温度计的示数 t。

5、当温度升高到一定值后，停止加热，让金属棒自然冷却，再次测量室温下金属棒的长度 L₂，以检验实验的重复性。

五、实验数据记录与处理｜温度 t（℃）｜标尺读数 n（mm）｜｜｜｜｜ 20 ｜ 250 ｜｜ 40 ｜ 305 ｜｜ 60 ｜ 360 ｜｜ 80 ｜ 415 ｜｜ 100 ｜ 470 ｜1、计算温度的变化量Δt：Δt ＝ t t₁2、计算每次温度变化对应的标尺读数变化量Δn：Δn ＝ n n₁3、计算金属棒的伸长量ΔL：ΔL ＝b·Δn ／ 2D4、根据线胀系数的表达式，计算不同温度下的线胀系数α，并求平均值。

金属线胀系数的测定--南昌大学-物理实验LT一、 实验原理：一般固体的体积或长度，随温度的升高而膨胀，这就是固体的热膨胀。

绝大多数固定材料，其长度是随温度的升高而增加的，这一现象称为线膨胀。

设物体的温度改变∆t 时其长度改变量为∆L ，如果∆t 足够小，则∆t 与∆L 成正比，并且也与物体原长L 成正比，因此有∆L =αL ∆t上式中比例系数α称为固体的线膨胀系数，其物理意义是温度每升高1℃时物体的伸长量与它在0℃时长度之比。

设在温度为0℃时，固体的长度为L 0,当温度升高t 时，其长度为L t ，则有(L t −L 0)/ L 0=αt即L t = L 0（1+αt ）如果金属杆在温度为t 1，t 2时，其长度分别为L 1，L 2，则可得出L 1= L 0（1+αt ） L 2= L 0（1+αt ）又因为L 1与L 2非常接近，所以L 1/L 2≈1，于是可得到如下结果：α=(L 2−L 1)L 1(t 2−t 1)所以，测得L 1，L 2，t 1和t 2，就可求得α值二、 实验内容和步骤：1. 接通电加热器与温控仪输入输出接口和温度传感器的航空插头。

2. 使金属杆一端与隔热顶尖紧密接触。

3. 调节千分表带绝热头的测量杆，使其刚好与金属杆的自由端接触。

4.接通恒温控制仪的电源，设定需要加热的值为65℃，按确定键开始加热，在达到设定温度后降温至室温，降温时也应读数。

注视恒温控制仪，每隔5℃读一次读数，同时读出千分表的示数，将相应的读数t 1，t 2…t n ，n 1，n 2…n n 记在表格里。

5. 显然，金属杆各时刻上升的温度是t 2-t 1，t 3-t 2，…，t n -t n−1，相应的伸长量是n 2-n 1，n 3-n 2，…，n n -n n−1，则n n -n 1=αL 1（t n -t 1）即α=(n 2−n 1)L 1(t 2−t 1)=∆nL 1∆t由此可知，线膨胀系数α是以n n -n 1为纵坐标、以t n -t 1为横坐标的实验曲线的斜率。

南昌大学物理实验报告
课程名称：大学物理实验
实验名称：金属线胀系数的测定
学院：XX XX学院专业班级：XXX１６４班学生姓名：XXX学号：XXXXX１６１２4实验地点：基础实验大楼座位号：XX
实验时间：第２周星期四上午三四五节课
不确定度计算
七、实验总结
1.本次实验的原理比较简单，操作其实也并不复杂。

但是在加热过程中需要较长的时间，而且必须时时注意温度的变化，这需要我们有一定的耐心。

2.再进一步深入了解了逐差法分析数据的方法。

3.了解到了科学试验的严谨性。

八、附上原始数据：。

金属线胀系数的测定实验实训报告 .doc一、实验目的1、了解不同金属导热系数差异；2、掌握测量不同金属杆的热胀系数方法；3、了解热胀现象在实际应用中的作用。

二、实验原理金属杆的热胀系数通常用于当温度发生变化时，在长度、体积等方面的变化率，即“热膨胀系数”的描述数量。

物体受热时，体积会发生变化，通常是增加；当冷却时，则会收缩。

对于金属杆的热胀系数，其公式为：α=ΔL/L*ΔT，其中ΔL 表示长度变化量，L 表示本来的长度，ΔT表示温度变化量，α表示热胀系数。

三、实验仪器1、热膨胀测量仪；2、实验用的固定导杆；3、温度计；4、电源供电线。

四、实验方法1、将测量所用导杆固定在热膨胀测量仪上；2、测量热膨胀仪的初始长度；3、将电源线插入热膨胀仪，并接上电源，使热源加热；4、通过温度计监测温度变化，当设定温度点时，记录导杆的长度；5、计算出不同温度下导杆的长度变化和热膨胀系数。

五、实验结果与分析经过实验，我们得到了铜、铝、钢三种材质的热胀系数数据，分别如下表所示：材质实验重量（g）实验长度（cm）温度变化量（℃）热胀系数（10^-6/℃）铜764.898 17.69 40 12.301铝418.456 17.78 40 24.073钢393.896 17.77 40 11.719从上表可以看出，不同金属的热胀系数是不同的，铝材的热膨胀系数最大，为24.073×10^-6/℃，而铜材的热膨胀系数最小，仅为12.301×10^-6/℃；钢材和铜材的差别较小，分别为11.719×10^-6/℃和12.301×10^-6/℃。

此处实验结果得到的不同材质的热膨胀系数，与实际珠宝材料制作、航空航天领域等的应用密切相关，了解不同材质的热膨胀系数，有助于实际生产领域中的应用与改进。

六、实验结论通过本次实验，我们得出了不同金属的热膨胀系数数据，并分析了数据的差异，了解到热胀现象在实际应用中的重要性。

金属线胀系数的测定实验报告引言金属的线胀系数是指在温度变化时，金属材料长度的变化比例。

了解金属线胀系数对于工程设计和材料研究非常重要。

本实验将通过测量金属线在不同温度下的长度变化，来确定金属的线胀系数。

实验步骤1. 准备实验材料和设备•实验材料：选择一种金属线作为实验样品，例如铁丝或铜丝。

•实验设备：恒温水槽、温度计、游标卡尺、计时器。

2. 设置实验条件•将恒温水槽的温度设置在一个合适的范围，例如从室温开始逐渐升高到80°C。

•使用温度计测量恒温水槽内的温度，并记录下来。

3. 测量金属线的长度•在室温下，使用游标卡尺测量金属线的初始长度，并记录下来作为参考值。

•将金属线放入恒温水槽中，确保其完全浸入水中。

•等待一段时间，让金属线与水的温度达到平衡。

•再次使用游标卡尺测量金属线的长度，并记录下来。

4. 重复测量•重复步骤3，但每次将温度升高一定的步长，例如每次升高10°C，直到达到设定的最高温度。

数据处理与分析1. 计算金属线的线胀系数•对于每个温度点，计算金属线的长度变化。

•根据公式ΔL = α * L * ΔT，计算金属线的线胀系数α，其中ΔL 是长度变化，L 是初始长度，ΔT 是温度变化。

2. 绘制实验结果图表•使用数据绘制温度与金属线线胀系数之间的变化曲线图表。

•横轴为温度，纵轴为线胀系数。

•根据曲线的趋势，分析金属线胀系数与温度的关系。

结论通过该实验，我们成功测定了金属线的线胀系数，并绘制了线胀系数随温度变化的曲线图。

根据实验结果，可以得出金属线的线胀系数随温度的升高而增加的结论。

这对于工程设计和材料研究中的热膨胀问题具有重要意义。

参考文献(这里列出你在写实验报告时参考的任何文献、资料等信息)。