2015年达州第二次诊断考试文科数学答案
- 格式:doc
- 大小:462.00 KB
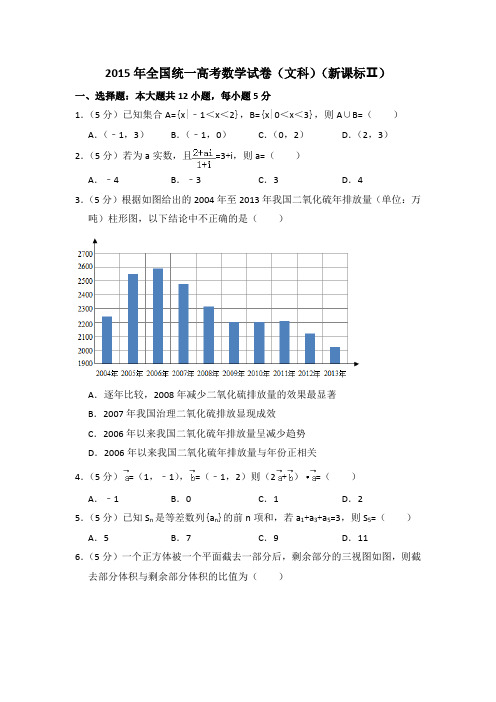
- 文档页数:5


达州市普通高中2015届第一次诊断性测试数学(文)试题参考答案1-5 C DB A A 6-10 C D B B C11.180,12. 0或31,13.-4, 14.⎩⎨⎧=-=56y x , 15.②③④16解:(Ⅰ)()(),cos ,cos ,,B C n c b m == ;cos 2A a n m -=⋅()分分分6 (3)24 (21)cos cos sin 2sin sin 2cos sin 2cos sin cos sin ;cos 2cos cos π=∴-=∴-==+∴⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=+∴-=+=⋅∴A A AA A CB A A BC C B A a B c C b n m (Ⅱ)分得由8....................................................12cos 2123222222=++∴-+===bc c b Abc c b a a分分又12.............................................................210. (43)sin 21==∴=∴==∆c b bc A bc S17解:(Ⅰ)设甲答错的3道题为321..A A A ,答对的2道题为21.B B , 则从中选3题的所有可能有:213212232132211231131221121321,,,,,,,,B B A B B A B A A B A A B B A B A A B A A B A A B A A A A A ,共10种,其中得15分(两对一错)的有3种,所以乙得15分的概率为103;...........................................6分(Ⅱ)不妨设(Ⅰ)中的321..A A A 为乙答对的3题,21.B B 为乙答错的2道题,则从中选3题的所有可能有:213212232132211231131221121321,,,,,,,,B B A B B A B A A B A A B B A B A A B A A B A A B A A A A A ,也是10种,则乙得15分(两对一错)的有6种,得30分(全对)的只有1种,所以乙入选(两对一错或全对,)的概率为107..........................12分 18解:(Ⅰ)由θ=∠POC ,ABCD 为距形,2=OC 得分3...............................cos 2,sin 2θθ===OB BC AD又θsin 245==∴=∠AD OA POQ ,分),,(5..............................40sin 2cos 2⎪⎭⎫⎝⎛∈-=-=∴πθθθOA OB AB(Ⅱ)由(Ⅰ)得()BC AB f S ABCD ⋅==θ ()θθθsin 2sin 2cos 2⋅-=θθθ2sin 2cos sin 2-⋅= θθ2cos 12sin +-=142sin 2-⎪⎭⎫ ⎝⎛+=πθ ⎪⎭⎫⎝⎛∈40πθ,............8分 ⎪⎭⎫⎝⎛∈+∴43,442πππθ()θπθπππθf y =⎪⎭⎫ ⎝⎛∈⎪⎭⎫⎝⎛∈+∴时,,即当8,02,442为增函数; ()θππθπππθf y =⎪⎭⎫⎝⎛∈⎪⎭⎫ ⎝⎛∈+∴时,,即,当4843242为减函数;()θf y =∴的增区间为⎪⎭⎫ ⎝⎛80π,,减区间为⎪⎭⎫⎝⎛48ππ,..................10分()128max -=⎪⎭⎫⎝⎛=∴πθf f ..............................12分 19解:(Ⅰ)因为()1+n n a a ,在函数()的21+-=x x f 图象上,211+-=∴+n n a a 又,11+=n n a b 11112111211111111=+-++=+-++-=+-+=-++n n n n n n n n n a a a a a a a b b .........4分又()2101-==f a,21111=+=∴a b {}n b ∴是以2为首项,1为公差的等差数列;),(*1N n n b n ∈+=∴;..........................6分(Ⅱ)由(Ⅰ)得111+=+=n n a n b1+-=∴n na n又Kn a n >对*∈N n 恒成立,得min 11⎪⎭⎫⎝⎛+-<n K ..................8分 而11+-n 在*∈N n 为递增数列,...................10分所以2111min -=⎪⎭⎫⎝⎛+-n 21-<K ..................................12分20解:(Ⅰ)因为当0≥x 时,()44313+-=x x x f ;()()()()()()()()[][)()()(][]()()()40,34220,22,,0,2,2,0,00,2,02,0224''2'=-==---∞-=≤∴=+∞=≥∴>+∞∈<∈∴-+=-=∴f f f x f y x x f y x f y x x f x x f x x x x x f 又,增区间为的减区间为时当为偶函数,又,增区间为的减区间为时当;时当时当 综上得:()(][]2,02,,的减区间为-∞-=x f y ,[][)∞+-,,增区间为20,2极大值为:()40=f ,极小值为:()()3422-==-f f ...............6分(Ⅱ)由(Ⅰ)得()x f y =在[]2,0为减函数,在[]3,2为增函数又()()⎪⎭⎫ ⎝⎛--==-=34,034,13,342恒过点kx y f f (),时过点又971,334=-=k kx y ,时过点034,234=⎪⎭⎫ ⎝⎛--=k kx y时,⎥⎦⎤⎢⎣⎡∈∴97,0k 集合{()}34-=kx x f x 有两个元素,...............9分又()x f y =是定义在R 上的偶函数,同理可得时,⎥⎦⎤⎢⎣⎡-∈∴0,97k 集合{()}34-=kx x f x 也有两个元素,综上得⎥⎦⎤⎢⎣⎡-∈∴97,97k ..........................................13分()()()()()()()()()()()()()()()分为增函数;为减函数,在在,时当时当时当解:3..................................001,00,10,0,00,111111',11ln ,1.21min''22==∴-=∴>+∞∈<-∈∴+=+-++=∴+-++==I f x f x f y x f x x f x x xx x x f x xx x f a(Ⅱ)()()()0,1ln 2>+--++=a aax xa a x x f ()()()22'111a x aa x a x a a x x f +-+=+-++=∴,()()()()分为增函数;为减函数,在在,时当时当5.............................................111ln 1,11,0,1,01,min ''a a a a f x f a a a a a x f y x f a a x x f a a a x -+=⎪⎭⎫ ⎝⎛+-=∴⎪⎭⎫⎝⎛+∞+-⎪⎭⎫ ⎝⎛+--=∴>⎪⎭⎫⎝⎛+∞+-∈<⎪⎭⎫ ⎝⎛+--∈∴又()x f y =有两个零点,()()()22'1110ln 110111ln aaa a a h a a aa h aa -=-=>--=<-+∴则令 ()()()()()()()()()()()()()()分综上:时当时当又减为函数;为增函数,在在,时当时当8.......................................................,11,00,,1,0,1,001,11,00,1,01,0''+∞⋃∈<+∞∈<∈∴=+∞=∴<+∞∈>∈∴a a h a a h a h x f y x f a x f a()III 当1=a 时由(Ⅰ)得方程()0=-k x f 必存在两个异号实根21,x x ,且()21210x x x x <<<不妨设;()01=-k x f ,()02=-k x f()()()[]()[]()()()()()()()()()()()()0,0,1000,110 (0114111)1ln 11ln ,0,122222'>-∈∴==-∈∴≤-+-=--+=∴+--+--+-++=----=-∈x g x g x g y x x x x x x x x x g x xx x x x k x f k x f x g x 时当又为减函数,时,当分设时当()00111><<-x g x ,则又[()][()]()()()()()()()()分为增函数,在又14....................................................................0,0,,0,1,000212121212111>+∴<-∴+∞=+∞∈∈-<-⇒-=<--∴>----∴x x x x x f y x x x f x f k x f k x f k x f k x f。

达州市普通高中2015届第二次诊断性测试评价报告命题组一、试题评价1.试卷结构时间120分钟。
难易比例为易:中:难=7:2:1。
考试内容为四川省2015届高考相同。
其主干知识的考察和分值分配均以《2015年全国普通高等学校统一招生考试数学考试大纲(四川省)》为依据。
全卷评阅统计结果的难度与预设难度吻合。
2.试题特点重视基础,全面考查,凸显重点。
全卷结合新课程特点和我市具体情况,强调基础。
文理科的第1~7题、第11~13题、第16题、第17题和第18题都是基础题,容易题和中档题,其中的很多题,读完题就能够得出结论(分值高达60分)。
试题涵盖四川省普通高中2015届学生在校学习的全部内容,但不是平均权重,重点知识重点考查,在知识交叉点和主干知识点设置试题。
函数、三角、立体几何、解析几何、数列和离散数学是主要内容,累计权重超过三分之二。
试卷亲和力强,由易到难坡度平缓。
除文理第8、9、10题、第15题、文第18题、理第17题外,所有试题入口宽,文第18题、理第17题和文理第20、21题这六个题的难度增加。
文科第17题第(II)问至少有两种解法,文科第20题打破理解析几何运算量大的限制,综合了圆和圆的切线,设点特殊,+的取值范围,减少难度,易于考生得分。
方便学生下手。
理科第20题,采用分步设问的方式,以求2k的范围来提示求λμ试卷评阅结果的部分统计数据表(理)试卷评阅结果的部分统计数据表(文)试题立足教材,坚持原创,题型常见,不偏不怪。
文理科试题来源于教材的习题各达三分之一,不回避学生最熟悉的内容。
考察结论性的知识点,不出怪题,不出特殊性结论的试题,文科第11题和第21题、理科第16题和第21题都是高中数学知识的常见题型,也是骨干知识。
有些题的最后结论虽然都有一定的难度,有些题作了过渡性第(I)问,掌握了相关知识后,是可以解决或者部分解决的。
适度创新,稳中求变。
这次诊断性考试,与平常的期末考试性质不同,不能在难度上一味降低,要符合高考要求,要根据高考试题的“三个有利于”来命制试题。

达州市普通高中2015届第一次诊断性测试数学试题(文科)本试卷分选择题和非选择题两部分,全卷共4页,第Ⅰ卷(选择题)1至2页,第Ⅱ卷(非选择题)3至4页,满分150分.考试时间120分钟.注意事项:1. 答题前,考生务必将自己的姓名、考号用0.5毫米黑色字迹的签字笔或钢笔填写在答题卡上,将条形码贴在答题卡规定的位置上.2. 选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上, 非选择题用0.5毫米黑色字迹的签字笔或钢笔书写在答题卡的对应框内,超出答题区书写的答案无效;在草稿纸、试题卷上的答案无效.3. 考试结束后,将答题卡收回.第Ⅰ卷(选择题,共50分)一.选择题:本大题共10个小题;每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1.已知全集U ={1,2,3,4,5},集合A ={1,2,3},B ={2,4}, 则(∁U A )∪B 为( )A .{1,2,4}B .{2,3,4}C .{2,4,5}D .{2,3,4,5} 2.设()()()()⎩⎨⎧>+≤-=10,1010,2x x f x x x f 则()2015f 的值为A .2B .3C .4D .53.如果复数()i i z +-=1,则( )A .|z |=2B .z 的实部为1 C.z 的共轭复数为1+i D .z 的虚部为-1 4. 在正项等比数列}{n a 中,3lg lg lg 963=++a a a ,则102a a 的值是 ( ) A. 100 B. 10 C. 9 D. 3 5. 定义某种运算⊙:S a =⊙b 的算原理如框图,则式子5⊙3+2⊙4= ( ) A .14 B .15C .16D .186.函数f(x)=sin(ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,如果x 1,x 2∈(-π6,π3),且f(x 1)=f(x 2),则f(x 1+x 2)=( )A.12B.22C.32D .17.某选手参加演讲比赛的一次评委打分如茎叶图所示,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为A . 86.5,1.5B .86.5,1.2C .86,1.5D .86,1.2 8 .下列说法正确..的是( ) A .命题“x ∀∈R ,0x e >”的否定是“x ∃∈R ,0<x e ” B .命题 “已知,x y ∈R ,若55,10≠≠≠+y x y x 或则”是真命题C .22x x ax +≥在[]2,0∈x 上恒成立⇔max min 2)()2(ax x x ≥+在[]2,0∈x 上恒成立”D .命题:若1a =-,则函数()221f x ax x =+-只有一个零点的逆命题为真命题。

四川省达州市2015年中考数学试卷一、选择题(共10小题,每小题3分,满分30分在每小题给出的四个选项中,只有一项符合要求)1. 2015的相反数是()A .B - -C 2015D - 201520152015考点:相反数.分析:根据只有符号不同的两个数互为相反数,可得一个数的相反数.解答:解:2015的相反数是:-2015 ,故选:D.点评:本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2. (3分)(2015?达州)一个几何体由大小相同的小方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是()考点:由三视图判断几何体;作图一三视图.3, 2, 3,据此可得出图分析:由已知条件可知,主视图有3列,每列小正方形数目分别为形.解答:解:根据所给出的图形和数字可得:主视图有3列,每列小正方形数目分别为3, 2, 3,则符合题意的是D;点评:本题考查几何体的三视图.由几何体的俯视图及小正方形中的数字,可知主视图有3列,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字. 左视图有3列,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.3. (3 分)(2015?达州)卜列运算止确的是()2 2A . a?a2=a2B. (a2) 3=a6- 2 3 6C. a +a =a6 2 3D. a ^a =a考点:同底数幕的除法;合并同类项;同底数幕的乘法;幕的乘方与积的乘方.专题:计算题.分析:A、原式利用同底数幕的乘法法则计算得到结果,即可做出判断;B、原式利用幕的乘方运算法则计算得到结果,即可做出判断;C、原式不能合并,错误;D、原式利用同底数幕的除法法则计算得到结果,即可做出判断.解答:解:A、原式=a3,错误;B、原式=a6,正确;C、原式不能合并,错误;4D、原式=a,错误,故选B.点评:此题考查了同底数幕的乘除法,合并同类项,以及幕的乘方与积的乘方,熟练掌握运算法则是解本题的关键.4. (3分)(2015?达州)2015年某中学举行的春季田径径运动会上,参加男子跳高的15名运动员的成绩如表所示:这些运动员跳高成绩的中位数和众数分别是()A .• 1.70m, 1.65m B. 1.70m, 1.70m (C . 1.65m, 1.60m D .3, 4考点:众数;中位数.分析:首先根据这组数据的个数是奇数,则处于中间位置的数就是这组数据的中位数,判断出这些运动员跳高成绩的中位数即可;然后找出这组数据中出现次数最多的数,则它就是这些运动员跳高成绩的众数,据此解答即可.解答:解:T 15十2=7…1,第8名的成绩处于中间位置,•••男子跳高的15名运动员的成绩处于中间位置的数是 1.65m,•••这些运动员跳高成绩的中位数是 1.65m;•••男子跳高的15名运动员的成绩出现次数最多的是 1.60m,•••这些运动员跳高成绩的众数是1.60m;综上,可得这些运动员跳高成绩的中位数是 1.65m,众数是1.60m.故选:C.点评:(1)此题主要考查了众数的含义和求法,要熟练掌握,解答此题的关键是要明确:①一组数据中出现次数最多的数据叫做众数. ②求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.(2)此题还考查了中位数的含义和求法,要熟练掌握,解答此题的关键是要明确:将一组数据按照从小到大(或从大到小)的顺序排列,①如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数•②如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.5. (3分)(2015?达州)下列命题正确的是()A .矩形的对角线互相垂直B .两边和一角对应相等的两个三角形全等C .分式方程——+仁一可化为一元一次力程X-2+ (2x- 1)= - 1.52z- 1 1- 2xD .多项式t2- 16+3t因式分解为(t+4)(t- 4)+3t考点:命题与定理.分析:根据矩形的性质,全等三角形的判定,分式方程的解法以及因式分解对各选项分析判断即可得解.解答:解:A、矩形的对角线互相垂直是假命题,故本选项错误;B、两边和一角对应相等的两个三角形全等是假命题,故本选项错误;C、分式方程上主+仁丄父两边都乘以(2x- 1),可化为一元一次力程x-2+ (2x2i- 1 1 - 2x-1)= - 1.5是真命题,故本选项正确;D、多项式t2- 16+3t因式分解为(t+4)(t- 4)+3t错误,故本选项错误.故选C.点评:本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题•判断命题的真假关键是要熟悉课本中的性质定理.6. (3分)(2015?达州)如图,△ ABC中,BD平分/ ABC, BC的中垂线交BC于点E,交BD于点F,连接CF •若/ A=60 ° / ABD =24 °则/ ACF的度数为()A .18°B.36°'C.30°D.24°/考点:线段垂直平分线的性质.分析:根据角平分线的性质可得/ DBC = / ABD=24°然后再计算出/ ACB的度数,再根据线段垂直平分线的性质可得BF = CF,进而可得/ FCB=24°,然后可算出/ ACF的度数.解答:解:T BD平分/ ABC,•••/ DBC= / ABD=24° ,•••/ A=60°,•••/ ACB=180°- 60° - 24° X2=72°,••• BC的中垂线交BC于点E,• BF=CF,•••/ FCB=24°•••/ ACF=72° - 24° =48°,故选:A .点评:此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.7. (3分)(2015?达州)如图,直径AB为12的半圆,绕A点逆时针旋转60 °,此时点B旋A . 12 nB . 24 n C. 6 n D. 36 n转到点B 则图中阴影部分的面积是()考点:扇形面积的计算;旋转的性质.分析:根据题意得出AB=AB' =12 / BAB ' =60。

遂宁市高中2015届第二次诊断性考试数学(文科)参考答案及评分意见一、选择题:每小题5分,满分50分 二、填空题:每小题5分,满分25分11.222=+y x 12.(0,4) 13.4 14.75 15.①③④ 三、解答题:满分75分 16.(本小题满分12分)解:(1)因为)2,4(ππ∈A ,所以)43,2(4πππ∈+A ,又102)4cos(-=+πA , 所以1027)4(cos 1)4sin(2=+-=+ππA A ................3分 所以544sin)4cos(4cos)4sin(]4)4sin[(sin =+-+=-+=ππππππA A A A 。
..............6分(2)23)21(sin 2sin 21sin 22cos sin 2)(22+--=-+=+=x x x x x x f ,因为x R ∈ 所以sin [1,1]x ∈-,从而当1sin 2x =时()f x 取得最大值32 ...............12分17.(本小题满分I2分)解: (1)由题意知,该校共有老师60名,故某老师被抽到的概率P=151604=。
设该学科攻关小组中男老师的人数为x ,则46045x=,解得x =3,所以该学科攻关小组中男、女老师的人数分别为3,1。
...............5分 (2)由(1)知,记3名男老师分别为1a ,2a ,3a ,1名女老师为b ,则选出2名老师的所有基本事件为(21,a a ), (31,a a ),(b a ,1),(32,a a ),(b a ,2),(b a ,3), (12,a a ),(13,a a ),(1,a b ),(23,a a ),(2,a b ),(b,3a ),共12个, ...............8分 恰有1名女老师的基本事件为(b a ,1),(b a ,2),(b a ,3),(1,a b ),(2,a b ),(b,3a ) 共6个 ...............11分 所以选出的2名老师中恰有1名女老师的概率21126==p ...............12分18.(本小题满分12分) 证明: (1)连结BD90BAD ADC ∠=∠=,AB a DA =所以2BD DC a ==E 为BC 中点所以BC DE ⊥ ……………3分 又因为PD ⊥平面ABCD , 所以BC PD ⊥ 因为DEPD D = ……………4分所以BC ⊥平面PDE ……………5分 因为BC ⊂平面PBC ,所以平面PBC ⊥平面PDE ……………6分 (2)当点F 位于PC 三分之一分点(靠近P 点)时, //PA 平面BDF ……………7分 连结,AC BD 交于O 点//AB CD ,所以AOB ∆相似于∆又因为12AB DC =,所以12AO =从而在CPA ∆中,13AO AC = ……10分而13PF PC =所以//OF PA ………11分 而OF ⊂平面BDFPA ⊄平面BDF所以//PA 平面BDF ………12分19.(本小题满分12分)解:(1)∵71613162a a d d d =+⇒=+⇒=所以1(1)21n a a n d n =+-=- ...............5分 (2)∵数列}{n b 满足11+⋅=n n n a a b∴)121121(21)12)(12(111+--=+-=⋅=+n n n n a a b n n n ,∴12)1211215131311(21+=+--++-+-=n n n n T n ...............8分 要使不等式8n T n λ<+(*∈N n )恒成立,只需不等式1782)12)(8(++=++<n n n n n λ恒成立即可 ...............10分∵882≥+nn ,等号在2=n 时取得,∴25<λ ...............12分20.(本小题满分13分)解:(1)(10)F ,,设()P x y ,为E12= ∴ 22143x y +=。

达州市普通高中2018届第二次诊断性测试数学试题(文科)第Ⅰ卷(选择题,共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数()()()1a i i a R ++∈为纯虚数,则a 的值为( ) A .1- B .0 C .1 D .22.已知集合(){}|20A x x x =-≥,(1,4]B =-,则A B ⋃=( ) A .[]0,2 B .R C .(1,4]- D .[](1,0]2,4-⋃3.数列{}n a 中,若()*1312,n n S a n n N -=-∈…,11a=,则2a =( )A .4B .3C .2D .14.运行如图所示的程序框图,若输入n 的值为2,则输出的i 为( )A .3B .4C .5D .6 5.已知命题p :0a =,q :2()||()f x x x a x =++∈R 为偶函数,则p 是q 成立的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件6.如图,在正三棱柱111ABC A B C -中,D 为11B C 的中点,则下列说法正确的是( )A .1CC 与BD 是异面直线B .几何体11A DC ABC -为棱台且体积为原棱柱体积的56C .1AC P 面1A BD D .CD ⊥平面1A BD7.若实数,x y 满足不等式组202100x y x y y ++≥⎧⎪++<⎨⎪⎩…,则4z x y =+的取值范围为( )A .[]7,2--B .[7,1)--C .()7,1--D .[2,1)- 8.若[]2,2k ∈-,则直线y kx k =+与圆()2211x y -+=相交的概率为( )A.6 B.2 C.4 D.29.函数2()2cos2x f x x a =+-在110,6π⎛⎫⎪⎝⎭上有两个不同的零点,则实数a 的取值范围为( ) A .[1,1)(2,3]-⋃ B .()()1,12,3-⋃ C .()2,3 D .()()2,01,2-⋃10.某湖泊的水位h (单位:米)随时间t (单位:小时)的变化规律如下:122(0,0)t th m m t -=⋅+>…,若该湖泊的水位总不低于2米,则m 的取值范围是( )A .[2,)+∞B .[1,)+∞C .1[,)2+∞ D .1[,)4-+∞11.F 是双曲线2222:1(0,0)x y C a b a b-=>>的左焦点,M 是双曲线右支上一点,直线MF 切圆222x y a +=于点N ,2OF OM ON +=u u u r u u u u r u u u r,则C 的离心率是( )AB .2 CD12.已知偶函数()f x 的定义域是{}|0x R x ∈≠,()f x '是()f x 的导数,()()12f x xf x x'+>.不等式()22()ln 1(1)ln 20x f x x f ++--„的解集是( )A .(,1][1,)-∞-⋃+∞B .[1,0)(0,1]-⋃C .(,1]-∞-D .(0,1]第Ⅱ卷(非选择题,共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.“光明天使”基金收到甲乙丙三兄弟24万、25万、26万三笔捐款(一人捐一笔款),记者采访这三兄弟时,甲说:“乙捐的不是最少.”乙说:“甲捐的比丙多.”丙说:“若我捐的最少,则甲捐的不是最多.”根据这三兄弟的回答,确定乙捐了_________万.14.已知向量()2,a t =r ,()1,2b =-r ,且a b r r P ,则||a b -=r r.15.过抛物线24y x =的焦点倾斜角为6π的直线交抛物线于,A B 两点,则||AB = . 16.如图所示,要修建一个形状为等腰直角三角形的广场ABC ,90ABC ∠=︒,且在广场外修建一块三角形草地BCD ,满足2BD =,1CD =,欲使A 、D 之间距离最长,则BDC ∠=________(用弧度作答).三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17.已知等差数列{}n a ,公差0d >,且12312a a a ++=,将1a ,2a ,3a 分别加上2,4,10后成为等比数列{}n b 中3b ,4b ,5b 项.(1)求数列{}n a ,{}n b 的通项公式; (2)求数列{}n n a b 前n 项的和n S .18.我省某市根据实际情况目前主要采取以下四种扶贫方式:第一,以工代赈方式.指政府投资建设基础设施工程,组织贫困地区群众参加工程建设并获得劳务报酬.第二,整村推进方式.指以贫困村为具体帮扶对象,帮扶对口到村,资金安排到村,扶贫效益到户.第三,科技扶贫方式,指组织科技人员深入贫困乡村实地指导、技术培训等传授科技知识.第四,移民搬迁方式.指对目前极少数居住在生存条件恶劣、自然资源贫乏地区的特困人口,实行自愿移民.该市为了2018年更好精准精细的落实脱贫攻坚各项任务,2018年初在全市贫困户(分一般贫困户和“五特”户两类)中随机抽取了5000户就目前的主要四种扶贫方式进行了问卷调查,支持每种扶贫方式的结果如下表:已知在被调查的5000户中随机抽取一户支持整村推进的概率为0.36.(1)现用分层抽样的方法在所有参与调查的贫困户中抽取50户进行深入访谈,问应在支持科技扶贫户数中抽取多少户?(2)虽然“五特”户在全市的贫困户所占比例不大,但本次调查要有意义,其中这次调查的“五特”户户数不能低于被调查总户数的9.2%,已知1530b ≥,58c ≥,求本次调查有意义的概率是多少? 19.如图,多面体ABCDE 中,面ACDE 为矩形,面ACDE ⊥面ABC ,AB BC ⊥.(1)求证:面ABE ⊥面BCD ;(2)已知多面体ABCDE 各顶点均在同一球面上,且该球的表面积为48π,DC =的体积取得最大值时求其侧视图的面积.20.已知P 是椭圆2222:1(0)x y C a b a b+=>>上一点,1F ,2F 是椭圆的左右焦点,12||2F F =,12||||PF PF +=(1)求椭圆C 的标准方程;(2)斜率为()0k k >的直线AB 过点1F ,和椭圆C 相交于A 、B 两点,且11AF F Bλ=u u u r u u u r,23λ+≤.求k 的取值范围. 21.已知()1()ln a af x e ex x x-=+-+(01a ≤≤, 2.71828e =L 是自然对数的底数). (1)求函数()f x 的单调区间;(2)曲线()y f x =在()()11,A x f x 、()()22,B x f x 处的切线平行,线段AB 的中点为()00,C x y ,求证:01x ≥.(二)选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点O 为极点,以x 轴为极轴建立极坐标系,曲线1C 的参数方程是22cos 2sin x y αα=+⎧⎨=⎩(α为参数). (1)求1C 的普通方程(写成标准形式)和极坐标方程; (2)曲线2C 的极坐标方程是4cos 1cos 2θρθ=-(22ππθ-剟,且0θ≠),1C 、2C 的一个交点为A (异于O ),求||OA .23.选修4-5:不等式选讲已知0m >,0n >,函数()|2|||f x x m x n =-++的最小值是3. (1)求证:26m n +=; (2)2m =,解不等式()4f x ≥.达州市普通高中2018届第二次诊断性测试文科数学参考答案及评分参考评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解答与本解答不同,可根据试题的主要考查内容比照评分参考制定相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再得分.3.解答右端所注分数,表示该生正确做到这一步应该得的累加分数. 4.只给整数分数.选择题不给中间分.一、选择题13.26 15.16 16.34π三、解答题 (一)必考题17.解:(1)∵已知等差数列{}n a ,公差0d >,且12312a a a ++=, ∴24a =.∴3b ,4b ,5b 分别为6-d ,8,14+d , ∴28(6)(14)d d =-+. 解得,2d =(10d =-已舍)∴2n a n =, 12n n b -= (2)∵2nn n a b n =⋅,∴231222322nn S n =⨯+⨯+⨯+⋯+⋅, ∴23212+22++(1)22n nn S n n =⨯⨯-⋅+⋅L12(1)2n n S n +=+-⋅.18.解:(1)∵支持整村推进户数为50000.361800⨯=户 ∴5000120010018003001600b c +=----=户, ∴501600165000⨯=(户),(2)∵200a =五特户户数不能低于被调查总户数的9.2% ∴50009.2%460⨯=∴60≥c 有意义,又1530≥b ,58≥c ,1600+=b c ,,b c 情况列举如下:(1530,70),(1531,69),(1532,68),(1533,67),(1534,66),(1535,65),(1536,64), (1537,63),(1538,62),(1539,61),(1540,60),(1541,59),(1542,58)共13种情况.∴1113P =19.解:(1)面ACDE 为矩形,面ACDE ⊥面ABC ∴AE BC ⊥,AB BC ⊥.∴BC ⊥平面ABE .又BC ⊂平面BCD , ∴面ABE ⊥面BCD(2)∵易知多面体ABCDE 中外接球球心在AD 上中点,由2448S R ππ==球,得AD =DC = ∴6AC =.又AB BC ⊥,ABC ∆为直角三角形, ∴当ABC ∆斜边AC 上的高等于132AC =时,体积取得最大值.此时其侧视图也为直角三角形,面积为132⨯⨯=.20.解:(1)由题意,12||22==F F c,122PF PF a +==.∴=a 1=c ,∴1b ==. ∴C 的标准方程是2212x y +=.(2)设11(,)A x y 、22(,)B x y (10>y ), 由条件可得,直线AB 的方程为y kx k =+,即1yx k=-. 又111(1,)AF x y =---uuu r ,122(1,)FB x y =+uuu r , ∵11AF FB λ=uuu r uuu r ,∴12y y λ=-. 由方程组221,1.2y x k x y ⎧=-⎪⎨⎪+=⎩得,222(12)20k y ky k +--=.∴122212k y y k +=+,212212k y y k=-+. ∴222212k y y k λ-+=+,解得222(1)(12)k y k λ=-+,22(1)(12)k y k λλ=--+1. ∴2222224(1)(12)12k k k kλλ-=--++,解得2212(1)121k λ=+--.∵32λ剟1≤≤k .21.解:(1)由函数1()()ln a a f x e e x x x-=+-+得,0x >,且2()()()a a x e x e f x x ---'=-. ∵01a ≤≤,∴10a a e e ->>>.由不等式()0f x '>得a a e x e -<<,由不等式()0f x '<得0a x e -<<,或a x e >. 所以()f x 的单调增区间是[]a a e e -,,()f x 的单调减区间是(0,]-a e ,[,)+∞a e . (2)因曲线()y f x =在11(()),A x f x 、22(,())B x f x 处的切线平行,所以1212()()()f x f x x x ''=≠,即2212121111()1()1aaaae e e e x x x x --+⋅--=+⋅--,∴1212()a ae e x x x x -+=+,∴21212()()4-++≥+aax x e e x x ,即124-+≥+a a x x e e .∵2-+≥=a a e e ,即42-≤+a ae e∴122+≥x x . ∴12012+=≥x x x . 22.解:(1)因曲线1C 的参数方程是22cos 2sin x y αα=+⎧⎨=⎩(α为参数),所以,曲线1C 的普通方程是()2224x y -+=.将cos x ρθ=,sin y ρθ=代入普通方程得,22(cos 2)(sin )4ρθρθ-+=, 化简得曲线2C 极坐标方程是4cos ρθ=. (2)∵曲线1C ,2C 的极坐标方程分别是4cos 12cos 2θρθ=-,4cos ρθ=,∴当2πθ=,0ρ=,即曲线1C ,2C 都经过极点.设(),A ρθ,∴4cos 4cos 1cos 2θθθ=-.∵22ππθ-≤≤,∴4πθ=±,∴ρ=±,∴||AB =23.(1)证明:∵0m >,0n >,()|2|||f x x m x n =-++∴3()()232x m n x n m f x x m n n x m x m n x ⎧⎪-+-<-⎪⎪⎛⎫=-++-⎨ ⎪⎝⎭⎪⎪⎛⎫-+>⎪ ⎪⎝⎭⎩剟,∴()f x 在区间(,]2m -∞单调递减,在区间[,)2m+∞单调递增. ∴min ()22m mf x f n ⎛⎫==+ ⎪⎝⎭. 由题意,32mn +=,即26m n +=. (2)解:∵2m =,由(1)可知,3(2)()4(21)3(1)x x f x x x x x -<-⎧⎪=-+-⎨⎪>⎩剟, 当1x ≤时,由()4f x ≥得,44x -+≥,解得,0x ≤. 当1x >时,由()4f x ≥得,34x ≥,解得,43x ≥. 所以,不等式()4f x ≥的解集是4(,0][,)3-∞⋃+∞.。

达州市普通高中2024届第二次诊断性测试数学试题(文科)注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数z 满足i1iz ,则z 的虚部是A .1i 2B .1i 2C .12D .122.设全集R U,{|12}A x x ≤,2{|40}B x x x ,则图中阴影部分对应的集合是A .{|12}x x ≤B .{|02}x x ≤C .{|10}x x ≤D .{|1}x x 03.下图是某地区2016-2023年旅游收入(单位:亿元)的条形图,则下列说法错误的是A .该地区2016-2019年旅游收入逐年递增B .该地区2016-2023年旅游收入的中位数是4.30C .经历了疫情之后,该地区2023年旅游收入恢复到接近2018年水平D .该地区2016-2023年旅游收入的极差是3.694.如图,在正方体1111ABCD A B C D 中,E 为AB 中点,P 为线段11C D 上一动点,过D E P ,,的平面截正方体的截面图形不可能是A .三角形B .矩形C .梯形D .菱形A2016-2023年旅游收入15.函数3cos ()22x xxf x的部分图象大致为A .B .C .D .6.cos147cos333cos57cos 63A .1B.2C.2D .127.已知实数a b ,满足22ba ,则42ab 最小值为A .4B .8C.D.8.双曲线2222:1(00)x y C a b a b,的左、右顶点分别为12A A ,,P 为C 上一点,若直线1PA 与直线2PA 斜率之积为2,则C 的离心率为ABC .2D .39.已知圆心为(0 1)M ,的M ⊙与直线1y x 相切,则直线1x 被M ⊙截得的弦长为A.B .1CD .210.已知向量(21) ,a ,(36) ,b ,若t c a b ,且3 a c b c ,则实数tA .3B .4C .5D .611.如图,灯笼的主体可看作将一个椭圆绕短轴旋转得到的,这样的旋转体称为椭圆体.已知椭圆22221(0)x y a b a b绕短轴旋转得到的椭圆体的体积和表面积可以用公式243V a b 和24(2)3S a ab 计算.若灯笼主体的体积为323,4a ≤,则该灯笼主体表面积取值范围为A .80(83 ,B .64(16]3,C .80(16]3 ,D .64(83,12.当0x ≥时,不等式2e (1)xax x ≥恒成立,则a 取值范围是A .(1],B .1(]e,C .(e] ,D .(3],xyOxyO二、填空题:本题共4小题,每小题5分,共20分.13.若“x a ”是“2log 1x ”的充分不必要条件,则a 的取值范围是.14.已知2111()|2|113 x x f x x x ,≤,,≤≤,则((3))f f.15.将函数22()2sin cos f x x x x x的图象向左平移(0)a a 个单位得到函数()g x 的图象.若(23g ,则a 的最小值为.16.在ABC △中,角A B C ,,的对边分别为a b c ,,,222sin a b c A ,点D在平面ABC 内,满足2DC DB ,6a ,则DA 的最大值为.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)等差数列{}n a 的前n 项和为n S ,18a ,且90S .(1)求n S ;(2)若{}n b 为等比数列,415S b,26b a ,求{}n b 通项公式.18.(12分)随着AI 技术的不断发展,人工智能科技在越来越多的领域发挥着重要的作用.某校在寒假里给学生推荐了一套智能辅导系统,学生可自愿选择是否使用该系统完成假期的作业.开学时进行了入学测试,随机抽取了100名学生统计得到如下列联表:(1)判断是否有95%的把握认为入学测试成绩优秀与使用智能辅导系统相关;(2)若把这100名学生按照入学测试成绩是否优秀进行分层随机抽样,从中抽取5人,再从这5人中随机抽取2人,则抽取的2人中恰1人的入学测试成绩优秀的概率.附:22()()()()()n ad bc K a b c d a c b d ,其中n a b c d .20()P K k ≥0.100.050.0250.0100k 2.7063.8415.0246.635使用智能辅导系统未使用智能辅导系统合计入学测试成绩优秀202040入学测试成绩不优秀402060合计604010019.(12分)如图,在直角梯形ABCD 中,AD BC ∥,AB BC ,3AB ,24BC AD ,把梯形ABCD 绕AB 旋转至11ABC D ,E F ,分别为1AB CC ,中点.(1)证明:EF ∥平面1CD A ;(2)若1π3DAD ,求点B 到平面11CDD C20.(12分)已知抛物线2:2(0)y px p ,直线:()l y k x p 与 交于A ,B 两点,线段AB 中点()m m M x y ,,2m ky .(1)求抛物线 的方程;(2)直线l 与x 轴交于点C ,O 为原点,设BOC △,COM △,MOA △的面积分别为BOC S △,COM S △,MOA S △,若BOC S △,COM S △,MOA S △成等差数列,求k .21.(12分)已知2()ln f x m x x,()2ln 2g x mx x .(1)当1m 时,求()f x 在点(1(1)) f ,处的切线方程;(2)令()()()h x g x f x ,当(1e) x ,时,判断()h x 零点的个数,并说明理由.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,曲线12cos :22sin x C y,( 为参数),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为cos 24.(1)求1C 的普通方程和2C 的直角坐标方程;(2)求以曲线1C 与曲线2C 的公共点为顶点的多边形面积.23.[选修4-5:不等式选讲](10分)设()|3||24|f x x x ,不等式()|1|f x m m ≥有解.(1)求m 取值范围;(2)记m 的最大值为n ,32a b c n ,求22252a b c ab 的最小值.C1C达州市普通高中2024届第二次诊断性测试文科数学参考答案一、选择题:1.D2.C3.B4.A5.A6.D7.B8.B9.D10.A11.C12.C二、填空题:本题共4小题,每小题5分,共20分.13.(2)+∞,14.115.7π1216.4+三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.解:(1)设等差数列{}n a 公差为d ,∵90S =,∴989802d ⨯⨯+=,∴2d =-,∴2(1)8(2)92n n n S n n n -=--=-.(2)4145s b ==,268102b a =-=-+=,∴数列{}n b 公比为12,∴1314(22n nn b --==.18.解:(1)∵2100(20202040)252.7783.841406040609k ⨯⨯-⨯==≈<⨯⨯⨯.∴没有95%的把握认为入学测试成绩优秀与使用智能辅导系统相关.(2)∵使用分层抽样,∴5人中2人成绩优秀,3人成绩不优秀,成绩优秀的2人记为1A ,2A ,成绩不优秀的3人记为1B ,2B ,3B ∴这5人中抽取2人的所有情况有:12A A ,11A B ,12A B ,13A B ,21A B ,22A B ,23A B ,12B B ,13B B ,23B B 共10种;其中恰好1人成绩优秀的有11A B ,12A B ,13A B ,21A B ,22A B ,23A B 共6种.∴抽取的2人中恰1人的入学测试成绩优秀的概率为35.19.(1)证明:设11D C 中点为G ,连接FG ,EG ,∵FG 为11CC D △中位线,1FG CD ∥,1CD ⊂平面1CD A ,FG ⊄平面1CD A ,∴FG ∥平面1CD A ,∵EG 为梯形11ABC D 中位线,1EG AD ∥,1AD ⊂平面1CD A ,EG ⊄平面1CD A ,∴EG ∥平面1CD A ,∵EG FG G = ,FG ⊂平面EFG ,EG ⊂平面EFG ,∴平面EFG ∥平面1CD A ,∵EF ⊂平面EFG ,∴EF ∥平面1CD A .(2)解:如图连接1BD ,∵AB BC ⊥,1AB BC ⊥,1BC BC B = ,∴AB ⊥平面1BCC ,1D 到平面1BCC 的距离为3,∵1BC BC =,1π3DAD ∠=,∴11113443322D BCC V -=⨯⨯⨯⨯=.等腰梯形11CDD C中可求11CD C S =△,设B 到平面11CDD C 的距离为h ,A CB E 1D 1C DF G∴1113B CDC V h -=⨯,∵1111D BCC B CD C V V --=,∴3h =.∴B 到平面11CDD C 的距离为3.20.解:(1)设11() A x y ,,22() B x y ,,∵22()y px y k x p ⎧=⎨=-⎩,,22220ky py p k --=,∴122p y y k +=,m p y k =.∵2m ky =,∴2p =,∴2:4y x Γ=.(2)∵24(2)y x y k x ⎧=⎨=-⎩,,2480ky y k --=,∴124y y k +=,128y y =-.∵BOC S △,COM S △,MOA S △成等差数列,∴2||y ,||m y ,1||||m y y -成等差数列.∴212||||||||m m y y y y =+-,∴123||||||m y y y =+,123||||m y y y =-,∴2212129()4m y y y y y =+-,22249()()32k k =+,∴4k =±.21.解(1)∵1m =,∴2()ln f x x x=+,(1)2f =,即切点为(12) ,,∵212()f x x x'=-,(1)1f '=-,∴(1(1)) f ,处切线方程为:30x y +-=.(2)∵2()()()2ln 2ln h x g x f x mx x m x x=-=-+--,∴2222(1)(2)()m x mx h x m x x x x--'=--+=,∵(1e) x ∈,,∴10x ->.当0m ≤时,20mx -<,()0h x '<,∴()h x 在(1e) ,上单调递减,∴()(1)0h x h m <=≤,()h x 无零点.当0m >时,令20mx -=,2x m=,若21m≤,即2m ≥时,()0h x '>,∴()h x 在(1e) ,上单调递增,∴()(1)0h x h m >=>,()h x 无零点.若21e m <<,即22e m <<时,2(1 x m ∈,,()0h x '<,()h x 单调递减,2(e) x m∈,,()0h x '>,()h x 单调递增,∴222()()42ln ln42ln 22ln ln 2ln h x h m m m m m m m m m m=---=--+-+≥,设()42ln 22ln ln 2ln F x x x x x x =--+-+,22ex <<,∴2()ln ln 2F x x x '=+-,设()()G x F x '=,22()0x G x x -'=<,即()G x 在2(2)e 上单调递减,()(2)10G x G >=>,即()0F x '>,∴()F x 在2(2)e 上单调递增,24()(20e eF x F >=->,即()0h x >,()h x 无零点.若2e m ≥,即20em <≤时,()0h x '<,∴()h x 在(1e) ,上单调递减,(1)0h m =>,2(e)e e h m m =--,∴2e 0e m m --≥,即222e e em -≤≤时,()h x 无零点.∴2e 0em m --<,即220e e m <<-时,()h x 有唯一零点.综上,220e e m <<-时()h x 有唯一零点,0m ≤或22e e m -≥时()h x 无零点.22.解:(1)221:(2)4C x y +-=2C :∵22(cos sin )4cos 4sin ρθθθθ-=-,∴2222cossin 4cos 4sin ρθρθρθρθ-=-,∵cos x ρθ=,sin y ρθ=,∴2244x y x y -=-,()()4()0x y x y x y +---=,∴()(4)0x y x y -+-=,∴2C 方程为0x y -=和40x y +-=.(2)∵22(2)40x y x y ⎧+-=⎨-=⎩解得00x y =⎧⎨=⎩,22x y =⎧⎨=⎩;∵22(2)440x y x y ⎧+-=⎨+-=⎩解得04x y =⎧⎨=⎩,22x y =⎧⎨=⎩.∴以曲线1C 与曲线2C 的公共点为顶点的多边形为三角形,其面积为4.23.解:(1)∵73()|3||24|31327 2. x x f x x x x x x x --⎧⎪=+--=--<⎨⎪->⎩,≤,,≤,,∴max ()5f x =,∴5|1|m m -+≥,解得3m ≤.所以m 的取值范围为(3] -∞,.(2)由(1)可得3n =,323a b c ++=,∴22222252()4a b c ab a b a c +++=+++2222221[()4](112)6a b a c =+++++213(32)62a b c ++=≥当且仅当441a b c ===时取等号,即22252a b c ab +++最小值为32.。

2015年普通高等学校招生全国统一考试(四川卷)数学(文史类)姓名 成绩一、选择题:本题共10个小题,每小题5分,共50分,在每个小题给出的四个选项中,只有一个是符合题目要求的。
1、设集合{|12}A x x =-<<,集合{|13}B x x =<<,则A B =( )()A {|13}x x -<< ()B {|11}x x -<< ()C {|12}x x << ()D {|23}x x <<2、设向量(2,4)a =与向量(,6)b x =共线,则实数x =( ) ()A 2 ()B 3 ()C 4 ()D 63、某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( ) ()A 抽签法 ()B 系统抽样法 ()C 分层抽样法 ()D 随机数法4、设,a b 为正实数,则"1"a b >>是22log log 0"a b >>的( )()A 充要条件 ()B 充分不必要条件 ()C 必要不充分条件 ()D 既不充分也不必要条件5、下列函数中,最小正周期为π的奇函数是( )()A cos(2)2y x π=+ ()B sin(2)3y x π=+ ()Csin 2cos 2y x x =+ ()D sin cos yx x =+6、执行如图所示程序框图,输出S 的值为( )()A ()B ()C 12- ()D 127、过双曲线2213y x -=的右焦点且与x ,A B 两点,则||AB =( )()A ()B ()C 6 ()D 8、某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系y e=( 2.718...e =为自然对数的底数,,k b 为常数)。

绝密 ★ 启封并使用完毕前2015年普通高等学校招生全国统一考试(四川卷)数 学(文史类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
满分l50 分。
考试时间l20分钟。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
第Ⅰ卷共10小题。
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{|(1)(2)0}A x x x =+-<,集合{|13}B x x =<<,则A B =(A ){}1|3x x -<< (B ){}|11x x -<< (C ){}|12x x << (D ){}|23x x <<【答案】A【解析】∵{|12}A x x =-<<,{|13}B x x =<<,{|13}A B x x ∴=-<<,选A.2.设向量(2,4)a =与向量(,6)bx =共线,则实数x =(A)2 (B)3 (C) 4 (D) 6 【答案】B【解析】由共线向量()11,a x y =,()22,b x y =的坐标运算可知12210x y x y -=, 即26403x x ⨯-=⇒=,选B.3.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是 (A)抽签法 (B )系统抽样法 (C )分层抽样法 (D )随机数法 【答案】C【解析】因为是为了解各年级之间的学生视力是否存在显著差异,所以选择分层抽样法。
4.设a ,b 为正实数,则“1a b >>”是“22log log a b >”的【答案】A【解析】由已知当1a b >>时,22log log 0a b >>∴,“1a b >>”是“22log log a b >”的充分条件。
2015年全国统一高考数学试卷(文科)(新课标Ⅱ)一、选择题:本大题共12小题,每小题5分1.(5分)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=()A.(﹣1,3)B.(﹣1,0)C.(0,2)D.(2,3)2.(5分)若为a实数,且=3+i,则a=()A.﹣4B.﹣3C.3D.43.(5分)根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是()A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关4.(5分)=(1,﹣1),=(﹣1,2)则(2+)=()A.﹣1B.0C.1D.25.(5分)已知S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=()A.5B.7C.9D.116.(5分)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.7.(5分)已知三点A(1,0),B(0,),C(2,)则△ABC外接圆的圆心到原点的距离为()A.B.C.D.8.(5分)如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为14,18,则输出的a=()A.0B.2C.4D.149.(5分)已知等比数列{a n}满足a1=,a3a5=4(a4﹣1),则a2=()A.2B.1C.D.10.(5分)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π11.(5分)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为()A.B.C.D.12.(5分)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)二、填空题13.(3分)已知函数f(x)=ax3﹣2x的图象过点(﹣1,4)则a=.14.(3分)若x,y满足约束条件,则z=2x+y的最大值为.15.(3分)已知双曲线过点且渐近线方程为y=±x,则该双曲线的标准方程是.16.(3分)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=.三.解答题17.△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC(Ⅰ)求.(Ⅱ)若∠BAC=60°,求∠B.18.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50,60)[60,70)[70,80)[80,90)[90,100)频数2814106(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大?说明理由.19.(12分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F 分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.20.椭圆C:=1,(a>b>0)的离心率,点(2,)在C上.(1)求椭圆C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.21.设函数f(x)=lnx+a(1﹣x).(Ⅰ)讨论:f(x)的单调性;(Ⅱ)当f(x)有最大值,且最大值大于2a﹣2时,求a的取值范围.四、选修4-1:几何证明选讲22.(10分)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.五、选修4-4:坐标系与参数方程23.(10分)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α≤π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,C3:ρ=2cosθ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.六、选修4-5不等式选讲24.(10分)设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd,则+>+;(2)+>+是|a﹣b|<|c﹣d|的充要条件.2015年全国统一高考数学试卷(文科)(新课标Ⅱ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分1.(5分)已知集合A={x|﹣1<x<2},B={x|0<x<3},则A∪B=()A.(﹣1,3)B.(﹣1,0)C.(0,2)D.(2,3)【考点】1D:并集及其运算.【专题】5J:集合.【分析】根据集合的基本运算进行求解即可.【解答】解:∵A={x|﹣1<x<2},B={x|0<x<3},∴A∪B={x|﹣1<x<3},故选:A.【点评】本题主要考查集合的基本运算,比较基础.2.(5分)若为a实数,且=3+i,则a=()A.﹣4B.﹣3C.3D.4【考点】A1:虚数单位i、复数.【专题】5N:数系的扩充和复数.【分析】根据复数相等的条件进行求解即可.【解答】解:由,得2+ai=(1+i)(3+i)=2+4i,则a=4,故选:D.【点评】本题主要考查复数相等的应用,比较基础.3.(5分)根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是()A.逐年比较,2008年减少二氧化硫排放量的效果最显著B.2007年我国治理二氧化硫排放显现成效C.2006年以来我国二氧化硫年排放量呈减少趋势D.2006年以来我国二氧化硫年排放量与年份正相关【考点】B8:频率分布直方图.【专题】5I:概率与统计.【分析】A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量减少的最多,故A正确;B从2007年开始二氧化硫排放量变少,故B正确;C从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C正确;D2006年以来我国二氧化硫年排放量越来越少,与年份负相关,故D错误.【解答】解:A从图中明显看出2008年二氧化硫排放量比2007年的二氧化硫排放量明显减少,且减少的最多,故A正确;B2004﹣2006年二氧化硫排放量越来越多,从2007年开始二氧化硫排放量变少,故B正确;C从图中看出,2006年以来我国二氧化硫年排放量越来越少,故C正确;D2006年以来我国二氧化硫年排放量越来越少,而不是与年份正相关,故D错误.故选:D.【点评】本题考查了学生识图的能力,能够从图中提取出所需要的信息,属于基础题.4.(5分)=(1,﹣1),=(﹣1,2)则(2+)=()A.﹣1B.0C.1D.2【考点】9O:平面向量数量积的性质及其运算.【专题】5A:平面向量及应用.【分析】利用向量的加法和数量积的坐标运算解答本题.【解答】解:因为=(1,﹣1),=(﹣1,2)则(2+)=(1,0)•(1,﹣1)=1;故选:C.【点评】本题考查了向量的加法和数量积的坐标运算;属于基础题目.5.(5分)已知S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=()A.5B.7C.9D.11【考点】85:等差数列的前n项和.【专题】35:转化思想;4A:数学模型法;54:等差数列与等比数列.【分析】由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3.再利用等差数列的前n项和公式即可得出.【解答】解:由等差数列{a n}的性质,a1+a3+a5=3=3a3,解得a3=1.则S5==5a3=5.故选:A.【点评】本题考查了等差数列的通项公式及其性质、前n项和公式,考查了推理能力与计算能力,属于中档题.6.(5分)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()A.B.C.D.【考点】L!:由三视图求面积、体积.【专题】11:计算题;5F:空间位置关系与距离.【分析】由三视图判断,正方体被切掉的部分为三棱锥,把相关数据代入棱锥的体积公式计算即可.【解答】解:设正方体的棱长为1,由三视图判断,正方体被切掉的部分为三棱锥,∴正方体切掉部分的体积为×1×1×1=,∴剩余部分体积为1﹣=,∴截去部分体积与剩余部分体积的比值为.故选:D.【点评】本题考查了由三视图判断几何体的形状,求几何体的体积.7.(5分)已知三点A(1,0),B(0,),C(2,)则△ABC外接圆的圆心到原点的距离为()A.B.C.D.【考点】J1:圆的标准方程.【专题】5B:直线与圆.【分析】利用外接圆的性质,求出圆心坐标,再根据圆心到原点的距离公式即可求出结论.【解答】解:因为△ABC外接圆的圆心在直线BC垂直平分线上,即直线x=1上,可设圆心P(1,p),由PA=PB得|p|=,得p=圆心坐标为P(1,),所以圆心到原点的距离|OP|===,故选:B.【点评】本题主要考查圆性质及△ABC外接圆的性质,了解性质并灵运用是解决本题的关键.8.(5分)如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为14,18,则输出的a=()A.0B.2C.4D.14【考点】EF:程序框图.【专题】27:图表型;5K:算法和程序框图.【分析】模拟执行程序框图,依次写出每次循环得到的a,b的值,当a=b=2时不满足条件a≠b,输出a的值为2.【解答】解:模拟执行程序框图,可得a=14,b=18满足条件a≠b,不满足条件a>b,b=4满足条件a≠b,满足条件a>b,a=10满足条件a≠b,满足条件a>b,a=6满足条件a≠b,满足条件a>b,a=2满足条件a≠b,不满足条件a>b,b=2不满足条件a≠b,输出a的值为2.故选:B.【点评】本题主要考查了循环结构程序框图,属于基础题.9.(5分)已知等比数列{a n}满足a1=,a3a5=4(a4﹣1),则a2=()A.2B.1C.D.【考点】88:等比数列的通项公式.【专题】54:等差数列与等比数列.【分析】利用等比数列的通项公式即可得出.【解答】解:设等比数列{a n}的公比为q,∵,a3a5=4(a4﹣1),∴=4,化为q3=8,解得q=2则a2==.故选:C.【点评】本题考查了等比数列的通项公式,属于基础题.10.(5分)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π【考点】LG:球的体积和表面积.【专题】11:计算题;5F:空间位置关系与距离.【分析】当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,利用三棱锥O﹣ABC体积的最大值为36,求出半径,即可求出球O的表面积.【解答】解:如图所示,当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,设球O的半径为R,此时V O﹣ABC=V C﹣AOB===36,故R=6,则球O的表面积为4πR2=144π,故选:C.【点评】本题考查球的半径与表面积,考查体积的计算,确定点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大是关键.11.(5分)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为()A.B.C.D.【考点】HC:正切函数的图象.【分析】根据函数图象关系,利用排除法进行求解即可.【解答】解:当0≤x≤时,BP=tanx,AP==,此时f(x)=+tanx,0≤x≤,此时单调递增,当P在CD边上运动时,≤x≤且x≠时,如图所示,tan∠POB=tan(π﹣∠POQ)=tanx=﹣tan∠POQ=﹣=﹣,∴OQ=﹣,∴PD=AO﹣OQ=1+,PC=BO+OQ=1﹣,∴PA+PB=,当x=时,PA+PB=2,当P在AD边上运动时,≤x≤π,PA+PB=﹣tanx,由对称性可知函数f(x)关于x=对称,且f()>f(),且轨迹为非线型,排除A,C,D,故选:B.【点评】本题主要考查函数图象的识别和判断,根据条件先求出0≤x≤时的解析式是解决本题的关键.12.(5分)设函数f(x)=ln(1+|x|)﹣,则使得f(x)>f(2x﹣1)成立的x的取值范围是()A.(﹣∞,)∪(1,+∞)B.(,1)C.()D.(﹣∞,﹣,)【考点】6B:利用导数研究函数的单调性.【专题】33:函数思想;49:综合法;51:函数的性质及应用.【分析】根据函数的奇偶性和单调性之间的关系,将不等式进行转化即可得到结论.【解答】解:∵函数f(x)=ln(1+|x|)﹣为偶函数,且在x≥0时,f(x)=ln(1+x)﹣,导数为f′(x)=+>0,即有函数f(x)在[0,+∞)单调递增,∴f(x)>f(2x﹣1)等价为f(|x|)>f(|2x﹣1|),即|x|>|2x﹣1|,平方得3x2﹣4x+1<0,解得:<x<1,所求x的取值范围是(,1).故选:B.【点评】本题主要考查函数奇偶性和单调性的应用,综合考查函数性质的综合应用,运用偶函数的性质是解题的关键.二、填空题13.(3分)已知函数f(x)=ax3﹣2x的图象过点(﹣1,4)则a=﹣2.【考点】36:函数解析式的求解及常用方法.【专题】11:计算题;51:函数的性质及应用.【分析】f(x)是图象过点(﹣1,4),从而该点坐标满足函数f(x)解析式,从而将点(﹣1,4)带入函数f(x)解析式即可求出a.【解答】解:根据条件得:4=﹣a+2;∴a=﹣2.故答案为:﹣2.【点评】考查函数图象上的点的坐标和函数解析式的关系,考查学生的计算能力,比较基础.14.(3分)若x,y满足约束条件,则z=2x+y的最大值为8.【考点】7C:简单线性规划.【专题】59:不等式的解法及应用.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).由z=2x+y得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点A时,直线y=﹣2x+z的截距最大,此时z最大.由,解得,即A(3,2)将A(3,2)的坐标代入目标函数z=2x+y,得z=2×3+2=8.即z=2x+y的最大值为8.故答案为:8.【点评】本题主要考查线性规划的应用,结合目标函数的几何意义,利用数形结合的数学思想是解决此类问题的基本方法.15.(3分)已知双曲线过点且渐近线方程为y=±x,则该双曲线的标准方程是x2﹣y2=1.【考点】KB:双曲线的标准方程.【专题】11:计算题;5D:圆锥曲线的定义、性质与方程.【分析】设双曲线方程为y2﹣x2=λ,代入点,求出λ,即可求出双曲线的标准方程.【解答】解:设双曲线方程为y2﹣x2=λ,代入点,可得3﹣=λ,∴λ=﹣1,∴双曲线的标准方程是x2﹣y2=1.故答案为:x2﹣y2=1.【点评】本题考查双曲线的标准方程,考查学生的计算能力,正确设出双曲线的方程是关键.16.(3分)已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=8.【考点】6H:利用导数研究曲线上某点切线方程.【专题】26:开放型;53:导数的综合应用.【分析】求出y=x+lnx的导数,求得切线的斜率,可得切线方程,再由于切线与曲线y=ax2+(a+2)x+1相切,有且只有一切点,进而可联立切线与曲线方程,根据△=0得到a的值.【解答】解:y=x+lnx的导数为y′=1+,曲线y=x+lnx在x=1处的切线斜率为k=2,则曲线y=x+lnx在x=1处的切线方程为y﹣1=2x﹣2,即y=2x﹣1.由于切线与曲线y=ax2+(a+2)x+1相切,故y=ax2+(a+2)x+1可联立y=2x﹣1,得ax2+ax+2=0,又a≠0,两线相切有一切点,所以有△=a2﹣8a=0,解得a=8.故答案为:8.【点评】本题考查导数的运用:求切线方程,主要考查导数的几何意义:函数在某点处的导数即为曲线在该点处的导数,设出切线方程运用两线相切的性质是解题的关键.三.解答题17.△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC(Ⅰ)求.(Ⅱ)若∠BAC=60°,求∠B.【考点】HP:正弦定理.【专题】58:解三角形.【分析】(Ⅰ)由题意画出图形,再由正弦定理结合内角平分线定理得答案;(Ⅱ)由∠C=180°﹣(∠BAC+∠B),两边取正弦后展开两角和的正弦,再结合(Ⅰ)中的结论得答案.【解答】解:(Ⅰ)如图,由正弦定理得:,∵AD平分∠BAC,BD=2DC,∴;(Ⅱ)∵∠C=180°﹣(∠BAC+∠B),∠BAC=60°,∴,由(Ⅰ)知2sin∠B=sin∠C,∴tan∠B=,即∠B=30°.【点评】本题考查了内角平分线的性质,考查了正弦定理的应用,是中档题.18.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表B地区用户满意度评分的频数分布表满意度评分分组[50,60)[60,70)[70,80)[80,90)[90,100)频数2814106(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:满意度评分低于70分70分到89分不低于90分满意度等级不满意满意非常满意估计哪个地区用户的满意度等级为不满意的概率大?说明理由.【考点】B8:频率分布直方图;CB:古典概型及其概率计算公式.【专题】5I:概率与统计.【分析】(I)根据分布表的数据,画出频率直方图,求解即可.(II)计算得出C A表示事件:“A地区用户的满意度等级为不满意”,C B表示事件:“B地区用户的满意度等级为不满意”,P(C A),P(C B),即可判断不满意的情况.【解答】解:(Ⅰ)通过两个地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值,B 地区的用户满意度评分的比较集中,而A地区的用户满意度评分的比较分散.(Ⅱ)A地区用户的满意度等级为不满意的概率大.记C A表示事件:“A地区用户的满意度等级为不满意”,C B表示事件:“B地区用户的满意度等级为不满意”,由直方图得P(C A)=(0.01+0.02+0.03)×10=0.6得P(C B)=(0.005+0.02)×10=0.25∴A地区用户的满意度等级为不满意的概率大.【点评】本题考查了频率直方图,频率表达运用,考查了阅读能力,属于中档题.19.(12分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F 分别在A1B1,D1C1上,A1E=D1F=4.过E,F的平面α与此长方体的面相交,交线围成一个正方形(Ⅰ)在图中画出这个正方形(不必说出画法和理由)(Ⅱ)求平面α把该长方体分成的两部分体积的比值.【考点】LF:棱柱、棱锥、棱台的体积;LJ:平面的基本性质及推论.【专题】15:综合题;5F:空间位置关系与距离.【分析】(Ⅰ)利用平面与平面平行的性质,可在图中画出这个正方形;(Ⅱ)求出MH==6,AH=10,HB=6,即可求平面a把该长方体分成的两部分体积的比值.【解答】解:(Ⅰ)交线围成的正方形EFGH如图所示;(Ⅱ)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8.因为EFGH为正方形,所以EH=EF=BC=10,于是MH==6,AH=10,HB=6.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.【点评】本题考查平面与平面平行的性质,考查学生的计算能力,比较基础.20.椭圆C:=1,(a>b>0)的离心率,点(2,)在C上.(1)求椭圆C的方程;(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与l的斜率的乘积为定值.【考点】K3:椭圆的标准方程;KH:直线与圆锥曲线的综合.【专题】5D:圆锥曲线的定义、性质与方程.【分析】(1)利用椭圆的离心率,以及椭圆经过的点,求解椭圆的几何量,然后得到椭圆的方程.(2)设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(x M,y M),联立直线方程与椭圆方程,通过韦达定理求解K OM,然后推出直线OM的斜率与l的斜率的乘积为定值.【解答】解:(1)椭圆C:=1,(a>b>0)的离心率,点(2,)在C上,可得,,解得a2=8,b2=4,所求椭圆C方程为:.(2)设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(x M,y M),把直线y=kx+b代入可得(2k2+1)x2+4kbx+2b2﹣8=0,故x M==,y M=kx M+b=,于是在OM的斜率为:K OM==,即K OM•k=.∴直线OM的斜率与l的斜率的乘积为定值.【点评】本题考查椭圆方程的综合应用,椭圆的方程的求法,考查分析问题解决问题的能力.21.设函数f(x)=lnx+a(1﹣x).(Ⅰ)讨论:f(x)的单调性;(Ⅱ)当f(x)有最大值,且最大值大于2a﹣2时,求a的取值范围.【考点】6B:利用导数研究函数的单调性;6E:利用导数研究函数的最值.【专题】26:开放型;53:导数的综合应用.【分析】(Ⅰ)先求导,再分类讨论,根据导数即可判断函数的单调性;(2)先求出函数的最大值,再构造函数(a)=lna+a﹣1,根据函数的单调性即可求出a的范围.【解答】解:(Ⅰ)f(x)=lnx+a(1﹣x)的定义域为(0,+∞),∴f′(x)=﹣a=,若a≤0,则f′(x)>0,∴函数f(x)在(0,+∞)上单调递增,若a>0,则当x∈(0,)时,f′(x)>0,当x∈(,+∞)时,f′(x)<0,所以f(x)在(0,)上单调递增,在(,+∞)上单调递减,(Ⅱ),由(Ⅰ)知,当a≤0时,f(x)在(0,+∞)上无最大值;当a>0时,f(x)在x=取得最大值,最大值为f()=﹣lna+a﹣1,∵f()>2a﹣2,∴lna+a﹣1<0,令g(a)=lna+a﹣1,∵g(a)在(0,+∞)单调递增,g(1)=0,∴当0<a<1时,g(a)<0,当a>1时,g(a)>0,∴a的取值范围为(0,1).【点评】本题考查了导数与函数的单调性最值的关系,以及参数的取值范围,属于中档题.四、选修4-1:几何证明选讲22.(10分)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=2,求四边形EBCF的面积.【考点】N4:相似三角形的判定.【专题】26:开放型;5F:空间位置关系与距离.【分析】(1)通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论;(2)通过(1)知AD是EF的垂直平分线,连结OE、OM,则OE⊥AE,利用S△ABC﹣S△AEF计算即可.【解答】(1)证明:∵△ABC为等腰三角形,AD⊥BC,∴AD是∠CAB的角平分线,又∵圆O分别与AB、AC相切于点E、F,∴AE=AF,∴AD⊥EF,∴EF∥BC;(2)解:由(1)知AE=AF,AD⊥EF,∴AD是EF的垂直平分线,又∵EF为圆O的弦,∴O在AD上,连结OE、OM,则OE⊥AE,由AG等于圆O的半径可得AO=2OE,∴∠OAE=30°,∴△ABC与△AEF都是等边三角形,∵AE=2,∴AO=4,OE=2,∵OM=OE=2,DM=MN=,∴OD=1,∴AD=5,AB=,∴四边形EBCF的面积为×﹣××=.【点评】本题考查空间中线与线之间的位置关系,考查四边形面积的计算,注意解题方法的积累,属于中档题.五、选修4-4:坐标系与参数方程23.(10分)在直角坐标系xOy中,曲线C1:(t为参数,t≠0),其中0≤α≤π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,C3:ρ=2cosθ.(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.【专题】5S:坐标系和参数方程.【分析】(I)由曲线C2:ρ=2sinθ,化为ρ2=2ρsinθ,把代入可得直角坐标方程.同理由C3:ρ=2cosθ.可得直角坐标方程,联立解出可得C2与C3交点的直角坐标.(2)由曲线C1的参数方程,消去参数t,化为普通方程:y=xtanα,其中0≤α≤π,α≠;α=时,为x=0(y≠0).其极坐标方程为:θ=α(ρ∈R,ρ≠0),利用|AB|=即可得出.【解答】解:(I)由曲线C2:ρ=2sinθ,化为ρ2=2ρsinθ,∴x2+y2=2y.同理由C3:ρ=2cosθ.可得直角坐标方程:,联立,解得,,∴C2与C3交点的直角坐标为(0,0),.(2)曲线C1:(t为参数,t≠0),化为普通方程:y=xtanα,其中0≤α≤π,α≠;α=时,为x=0(y≠0).其极坐标方程为:θ=α(ρ∈R,ρ≠0),∵A,B都在C1上,∴A(2sinα,α),B.∴|AB|==4,当时,|AB|取得最大值4.【点评】本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、曲线的交点、两点之间的距离公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.六、选修4-5不等式选讲24.(10分)设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab>cd,则+>+;(2)+>+是|a﹣b|<|c﹣d|的充要条件.【考点】29:充分条件、必要条件、充要条件;R6:不等式的证明.【专题】59:不等式的解法及应用;5L:简易逻辑.【分析】(1)运用不等式的性质,结合条件a,b,c,d均为正数,且a+b=c+d,ab>cd,即可得证;(2)从两方面证,①若+>+,证得|a﹣b|<|c﹣d|,②若|a﹣b|<|c﹣d|,证得+>+,注意运用不等式的性质,即可得证.【解答】证明:(1)由于(+)2=a+b+2,(+)2=c+d+2,由a,b,c,d均为正数,且a+b=c+d,ab>cd,则>,即有(+)2>(+)2,则+>+;(2)①若+>+,则(+)2>(+)2,即为a+b+2>c+d+2,由a+b=c+d,则ab>cd,于是(a﹣b)2=(a+b)2﹣4ab,(c﹣d)2=(c+d)2﹣4cd,即有(a﹣b)2<(c﹣d)2,即为|a﹣b|<|c﹣d|;②若|a﹣b|<|c﹣d|,则(a﹣b)2<(c﹣d)2,即有(a+b)2﹣4ab<(c+d)2﹣4cd,由a+b=c+d,则ab>cd,则有(+)2>(+)2.综上可得,+>+是|a﹣b|<|c﹣d|的充要条件.【点评】本题考查不等式的证明,主要考查不等式的性质的运用,同时考查充要条件的判断,属于基础题.。

2015普通高等学校招生全国统一考试Ⅱ卷文科数学第一卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合A={}{}=<<=<<-B A x x B x x 则,30,21 A.(-1,3) B.(-1,0 ) C.(0,2) D.(2,3) 1、选A (2)若a 实数,且=+=++a i iai则,312 A.-4 B. -3 C. 3 D. 42、解:因为.4,42)1)(3(2=+=++=+a i i i ai 所以故选D(3)根据下面给出的2004年至2013年我国二氧化碳年排放量(单位:万吨)柱形图,以下 结论中不正确的是27002600250024002300210020001900)A.逐年比较,2008年减少二氧化碳排放量的效果最显著; 排放显现成效;C.2006年以来我国二氧化碳排放量呈减少趋势;D.2006年以来我国二氧化碳年排放量与年份正相关。
3、选D(4)已知向量=•+-=-=a b a b a )则(2),2,1(),1,0( A. -1 B. 0 C. 1 D. 2 4、选B(5)设{}项和,的前是等差数列n a S n n 若==++5531,3S a a a 则A. 5B. 7C. 9D. 115、解:在等差数列中,因为.,5525)(,1,335153531A a a a S a a a a 故选所以==⨯+===++(6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为A.81 B.71 C. 61 D. 51 6、解:如图所示,选D.(7)已知三点)32()30(),01(,,,,C B A ,则ABC ∆外接圆的圆心到原点的距离为 A.35B. 321C. 352D. 34 7、解:根据题意,三角形ABC 是等边三角形,设外接圆的圆心为D ,则D (1,332)所以, .32137341==+=OD 故选B. (8)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”。

一、选择题(本题10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求)二、填空题(本题6个小题,每小题3分,共18分.把最后答案直接填在题中的横线上)11.-2 12.2 13.(40-x)(20+2x)=120014.94 15.4≤a <5 16.22n -3三、解答题(72分.解答时应写出必要的文字说明、证明过程或演算步骤)(一)(本题2个小题,共13分)17.(6分)解:原式=-1+1+12-(3-12)(3分)=12-3+12(5分)=1-3(6分)18.(7分)解:原式=a(a +2)(a -2)·a +2a(a -3)+1a -2(1分)=1(a -2)(a -3)+a -3(a -2)(a -3)(2分)=1+a -3(a -2)(a -3)=1a -3(3分)∵a,2,3是△ABC 的三边∴1 a 5且a 为整数(4分)∴a =2,3,4(5分)∵a 取2或3时,原分式无意义,所以a 只能取4(6分)当a =4时,原式=14-3=1(7分)(二)(本题2个小题,共15分)19.(7分)解:(1)40,20,30,(一空1分)(4分)(2)树状图(6分)所有可能:(A 1,A 2)(A 1,B 1)(A 1,B 2)(A 2,A 1)(A 2,B 1)(A 2,B 2)(B 1,A 1)(B 1,A 2)(B 1,B 2)(B 2,A 1)(B 2,A 2)(B 2,B 1)共12种,每种可能机会均等.P(一男一女参加比赛)=812=23(7分) 另解: 列表法:共12种可能,每种可能机会均等.P(一男一女参加比赛)=812=23(7分) 20.(8分)(1)解:设购买1台平板电脑x 元,购买1台学习机y 元.根据题意,得错误!(2分)解得错误!答:购买1台平板电脑3000元,购买1台学习机800元.(4分)(2)设购买平板电脑m 台,则学习机(100-m)台.根据题意,得错误!(5分)解得37127≤m ≤40 ∵m 取整数,∴一共有3种方案.(6分)方案一:平板电脑38台,学习机62台;方案二:平板电脑39台,学习机61台;方案三:平板电脑40台,学习机60台;(7分)方案一费用163600元,方案二费用165800元,方案三费用168000元,∵163600<165800<168000 另解:总费用y =3000m +800(100-m)y =2200m +80000∵2200>0,y 随m 的增大而增大∴当m 取38时,y 的值最小,y 的最小值为163600元∴方案一平板电脑38台,学习机62台最省钱(8分)(三)(本题2个小题,共15分)21.(7分)解:设AH 为x 米,则EH =(x +12)米在Rt △EHG 中,∵∠EGH =45°∴EH =HG =(x +12)米(2分)∵GF =DC =288米∴HF =x +12+288=(x +300)米(3分)在Rt △AHF 中,∵∠AFH =30°∴tan ∠AFH =AH HF 即x x +300=33(4分) 解得x =1503+150(6分)∵CF =HB =1.5米∴AB =HB +AH =1503+151.5≈411米∴凤凰山与中心广场的相对高度AB 为411米(7分)22.(8分)解:(1)连接AC 交BO 于点E ,过D 作DF ⊥OB 于点F.∵四边形ABCO 是菱形∴AE ⊥BO ,且BO =2EO∵tan ∠AOB =12∴AE EO =12设AE =x ,则EO =2x ,∵AE 2+EO 2=AO 2,AO = 5∴x 2+(2x)2=(5)2解得x 1=1,x 2=-1(舍去)∴AE =1,EO =2∴A(-2,1),B(-4,0)(1分)将A(-2,1),B(-4,0)代入y =k 1x +b得错误!解得错误!∴一次函数的关系式:y =12x +2(3分) ∵DF ⊥BO ,AE ⊥BO∴DF ∥AE∴△DFO ∽△AEO∵D 为AO 的中点 ∴DF AE =FO EO =12∴D(-1,12)(4分) 将D(-1,12)代入y =k 2x ,得k 2=-12∴反比例函数的表达式:y =-12x(5分) (2)由题意得错误!∴12x +b =-12x即x 2+2bx +1=0(6分) 当(2b)2-4×1×1=0时只有一个交点此时b =±1(7分)∴当-1<b <1时,一次函数y =k 1x +b 的图象与反比例函数y =k 2x的图象无交点(8分) (四)(本题2个小题,共17分)23.(8分)问题1:2,8(一空1分)(2分)问题2:2,6(一空1分)(4分)问题3:解:设学校每天的支出总费用为y 元则y =4900+10x +0.01x 2(5分)每天的生均投入为y x =4900x+10+0.01x(6分) 4900x =0.01x 时,y x的值最小 即x =700时,每天生均投入费用最低,最低费用24元.(8分)24.(9分)解:(1)DB =DA ,理由如下:∵CD 平分∠MCA∴∠MCD =∠DCA∵∠MCD +∠BCD =180°而∠BCD +∠BAD =180°∴∠MCD =∠BAD∵∠DCA =∠DBA∴∠DAB =∠DBA∴DB =DA(2分)(2)∵BC =AF∴BC =AF又∵∠DAB =∠DBA∴BCD =DFA∴CD =DF∴CD =DF又∵DB =DA∴△BCD ≌△AFD(5分)(3)过D 、O 作⊙O 的直径DN ,连接AN∵∠DCA =12∠MCA =60° ∴∠DNA =∠DCA =60°又∵DN 为⊙O 的直径∴∠DAN =90°∴DA =DN·sin ∠DNA=2×5×sin 60°=5 3在四边形ABDF 中,∠ABD +∠AFD =180°又∵∠DAB +∠DAE =180°,且∠DBA =∠DAB∴∠AFD =∠DAE又∵∠FDA =∠EDA∴△DAF ∽△DEA(7分)∴DA DE =DF DA即DA 2=DE·DF由(2)知:DF =DC =6∴DE =DA 2DF=(53)26=252(9分) (五)(本题12分)25.解:(1)将A(0,4),C(5,0)代入y =45x 2+bx +c 中 得:错误!(1分)解得b =-245,c =4 ∴该二次函数的表达式为:y =45x 2-245x +4(3分)(2)∵四边形OABC 是矩形∴DA ⊥y 轴又∵OD 平分∠AOC∴∠AOD =45°∴AO =DA =4∴D(4,4)又∵E 为BC 的中点BC =AO =4∴E(5,2)作D 点关于y 轴的对称点D′E 点关于x 轴的对称点E′(4分)连接D′E′分别交x 轴,y 轴于F 、G∵BD′=AD′+AB =AD +AB =9BE′=BC +CE′=BC +CE =4+2=6在Rt △BD′E′中,D′E′=BD′2+BE′2=92+62=313(6分)根据轴对称性得DG =D′G ,EF =E′F∴DG +GF +EF =D′E′=313又∵DE =BD 2+BE 2=12+22= 5∴四边形DEFG 周长的最小值为313+5(7分)(3)解:①过O 点作直线OF ⊥OD 与抛物线的对称轴交于点F ,再过点F 作直线MN ∥OD 交抛物线于P 1,P 2,交x 轴于点N ,交y 轴于点M ,在Rt △AOD 中OD =AD 2+AO 2=42+42=4 2∵抛物线的表达式为y =45x 2-245x +4 =45(x -3)2-165∴抛物线的对称轴为直线x =3,∴G(3,0),OG =3∵∠DOC =45°,∠DOF =90°∴∠COF =45°∴OG =GF∴OF =OG 2+GF 2=32+32=32(8分)∴S △P 1OD =S △P 2OD =12OD·OF =12×42×32=12 又∵MN ∥OD∴∠OMN =∠AOD =45° ∴OM =ON又∵OF ⊥MN在Rt △OMF 中OM =2·OF =2×32=6∴M(-6,0)∴直线MN 的表达式为:y =x -6由题意得方程组错误!解得:错误! 错误!∴P 1(29+418,-19+418),P 2(29-418,-19-418)(10分) ②在OF 的反向延长线上截取OF′=OF ,过F′作直线M′N′∥OD 分别与x 轴交于N′,与y 轴交于M′,与抛物线分别交于P 3、P 4,则S △P 3OD =S △P 4OD =12同理,直线M′N′的表达式为:y =x +6,由题意得方程组错误!解得:错误! 错误!∴P 3(29+10018,77+10018),P 4(29-10018,77-10018)(12分) 综上所述:抛物线上存在点P ,使△ODP 的面积为12.点P 的坐标分别为(29+418,-19+418) (29-418,-19-418) (29+10018,77+10018) (29-10018,77-10018)。

达州市普通高中2015届第二次诊断测试语文参考答案1.选C。
A.乘shènɡ→chénɡ;B.菲fēi→fěi;D.弄nònɡ→lònɡ。
2.选B。
A.迭→跌;C.荫→茵;D. 陨→殒3.选A。
往往:表示根据以往的经验,某种情况在一定条件下时常存在或经常发生。
此处正确。
B项“诟病”意为“指责”,为动词,此处误作名词使用。
这里可改为“还有一个广为诟病的原因”。
C项“光怪陆离”意为“形容现象奇异,色彩繁杂”,而句中“缤纷”也有“繁多而错杂”之意,故“光怪陆离”修饰“缤纷世界”,语意有重复,可删去“缤纷”,或改“缤纷”为“现实”。
D项“噤若寒蝉”意为“形容不敢作声”,此处用“不知所措”(不知道怎么办才好,形容受窘或发急)为好。
4.选D。
A项成分残缺,最后一分句“成为”的主语残缺,承前看主语是“圈子本身具有的排他性”,这就与“成为……重灾区”不搭配;此处可在“容易”前加“从而使得圈子”。
B项“最终目的是为了”犯了句式杂糅的毛病,应删去“目的”或“为了”。
C项“赋予……氛围”动宾搭配不当,可改“赋予”为“营造”。
5.B。
(A项无中生有,“‘道’比知识更重要”原文无据;C项以偏概全,“都是”错,原文是“多为”;D项混淆是非,“历久不衰”错,原文是“近代以来书院文化曾一度中断”)6.D。
(选项讲的是传统书院的间接优势)7.C。
(A项不能推出“达到了……目的”;B项不能推出“能者为师”;D项不能推出“传统书院办学理念”给“联合国教科文组织以极大的启发”)8.D。
( 虚,空着)9.C。
(A 表修饰;表递进。
B代词,代“他”;结构助词,用在主谓间取消句子独立性。
C介词,到。
D代词,他们的,自己)10.(1)于是他驾着车子,举着剑,拜访他的朋友,说:“孟尝君把我当成上客。
”(揭、过、客各1分,句意2分)(2)我暗自考虑,您宫中堆满了珍宝,宫外圈舍养满了狗马,堂下站满了美女。
您家里缺少的就是义罢了(窃、充及判断句式各1分,句意2分)11.焚券市义,谋复相位,(在薛)建立宗庙(答对1点1分,答对2点2分,答对3点4分)12.孟子对曰/地方百里而可以王/王如施仁政于民/省刑罚/薄税敛/深耕易耨/壮者以暇日修其孝悌忠信/入以事其父兄/出以事其长上/可使制梃以挞秦楚之坚甲利兵矣。

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1。
数列1,12,13,14,⋅⋅⋅的通项公式可能为( ) A .1na n=B .11nan =+ C .nan =D .12nan=【答案】A考点:数列的通项公式。
2.过两点()1,0-,()0,1的直线方程为( ) A .10x y -+= B .30x y --= C .20x y -=D .230x y --= 【答案】A 【解析】试题分析:过()0,1-,()1,0两点的直线两点式方程为)1(0)1(010----=--x y ,整理得:01=+-y x 。
考点:直线方程。
3。
sin 65cos35cos65sin35-=( )A .12B .22C .32D .1【答案】A 【解析】试题分析:根据两角差正弦公式的逆用知:2130sin )3565sin(35sin 65cos 35cos 65sin ==-=- . 考点:两角差正弦公式.4。
已知向量()3,7AB =,()C 2,3B =-,则1C 2-A =( ) A .1,52⎛⎫- ⎪⎝⎭B .1,52⎛⎫ ⎪⎝⎭C .1,52⎛⎫-- ⎪⎝⎭D .1,52⎛⎫- ⎪⎝⎭【答案】C 【解析】试题分析:)10,1(=+=BC AB AC ,则)5,21(21--=-AC . 考点:向量的坐标运算。
5。
a ,R b ∈,下列结论成立的是( )A .若a b <,则ac bc <B .若a b <,c d <,则ac bd <C .若a b <,则a c b c -<-D .若a b <,则nn a b <(n *∈N ,2n ≥)【答案】C考点:不等式的性质.6.设直线1:l 60x y -+=和直线2:l2230x y -+=,则直线1l 与直线2l 的位置关系为( )A .平行B .重合C .垂直D .以上都不是【答案】A 【解析】试题分析:由已知直线方程可知:362121≠--=,所以两直线平行。

2015年普通高等学校招生全国统一考试(四川卷)数学(文史类)姓名 成绩一、选择题:本题共10个小题,每小题5分,共50分,在每个小题给出的四个选项中,只有一个是符合题目要求的。
1、设集合{|12}A x x =-<<,集合{|13}B x x =<<,则A B =U ( )()A {|13}x x -<< ()B {|11}x x -<< ()C {|12}x x << ()D {|23}x x <<2、设向量(2,4)a =r 与向量(,6)b x =r共线,则实数x =( )()A 2 ()B 3 ()C 4 ()D 63、某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )()A 抽签法 ()B 系统抽样法 ()C 分层抽样法 ()D 随机数法4、设,a b 为正实数,则"1"a b >>是22log log 0"a b >>的( )()A 充要条件 ()B 充分不必要条件 ()C 必要不充分条件 ()D 既不充分也不必要条件5、下列函数中,最小正周期为π的奇函数是( )()A cos(2)2y x π=+ ()B sin(2)3y x π=+ ()Csin 2cos 2y x x =+ ()D sin cosy x x =+6、执行如图所示程序框图,输出S 的值为( )()A ()B ()C 12- ()D 127、过双曲线2213y x -=的右焦点且与x ,A B 两点,则||AB =( )()A ()B ()C 6 ()D 8、某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系kx by e+=( 2.718...e =为自然对数的底数,,k b 为常数)。

2015年普通高等学校招生全国统一考试(四川卷)数学(文科)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1、设集合A ={x|-1<x <2},集合B ={x|1<x <3},则A ∪B =(A){x|-1<x <3} (B){x|-1<x <1} (C){x|1<x <2} (D){x|2<x <3} 2、设向量a =(2,4)与向量b =(x,6)共线,则实数x =(A)2 (B)3 (C)4 (D)63、某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是(A)抽签法 (B)系统抽样法 (C)分层抽样法 (D)随机数法 4、设a,b 为正实数,则“a >b >1”是“log 2a >log 2b >0”的(A)充要条件 (B)充分不必要条件 (C)必要不充分条件 (D)既不充分也不必要条件 5、下列函数中,最小正周期为π的奇函数是(A)y =sin(2x +2π) (B)y =cos(2x +2π)(C)y =sin2x +cos2x (D)y =sinx +cosx 6、执行如图所示的程序框图,输出S 的值为(A)-32 (B) 32(C)-12 (D) 127、过双曲线2213y x -=的右焦点且与x 轴垂直的直线交该双曲线的两条渐近线于A 、B 两点,则|AB|= (A)433(B)23(C)6 (D)438、某视频保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y =e tx (e =2.718…为自然对数的底数,t,b 为常数)。
若该食品在6℃的保鲜时间是???小时,在72℃的保鲜时间是41小时 ,则该食品在33℃的保鲜时间是(A)16小时 (B)20小时 (C)24小时 (D)21小时9、设实数x,y 满足2102146x y x y x y +≤⎧⎪+≤⎨⎪+≥⎩,则xy 的最大值为(A)252 (B) 492(C)12 (D)14 10、设直线l 与抛物线y 2=4x 相较于A,B 两点,与圆(x -5)2+y 2=r 2(r >0)相切于点M ,且M 为线段AB 中点,若这样的直线l 恰有4条,则r 的取值范围是(A)(1,3) (B)(1,4) (C)(2,3) (D)(2,4) 二、填空题:本大题共5小题,每小题5分,共25分。
1达州市2015年普通高中三年级第二次诊断性检测数学试题(文科)参考答案及评分标准第Ⅰ卷(选择题,共50分)一、选择题1.(B) 2.(A) 3.(C) 4.(C) 5.(C) 6.(B) 7.(A) 8.(B) 9.(D) 10.(D)第Ⅱ卷(非选择题,共100分)二、11. 4 12. 56 13.13 14. 4 15.①②④ 三、解答题(本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤)16. 本题主要考查古典概型,互斥事件概率,分类讨论思想,简单图表信息识别,离散数学问题的一般表达.解:(Ⅰ)从所给表中随机抽取两名司机,共有15种抽法.……………………3分这些抽法是(A11,A12),(A11,A3),(A11,B1),(A11,B2),(A11,B3),(A12,A3),(A12,B1),(A12,B2),(A12,B3) (A3,B1),(A3,B2),(A3,B3),(B1,B2),(B1,B3),(B2,B3).……………………6分(Ⅱ)设事件“抽取的两名司机来自不同线路,且至少一名是男司机”为事件C,则C 包含(A11,A3),(A11,B2),(A11,B3),(A12,A3),(A12,B2),(A12,B3),(A3,B1),(A3,B2)共8个基本事件. ∴8()15P C =. 答:驾驶这辆客车的两个司机来自不同线路,且至少一名是男司机的概率为815.……12分 17. 本题主要考查数列的递推关系,数列前n 项和与项的关系,等差数列和等比数列的有关性质与方法,分类讨论思想.解:(Ⅰ)∵n S 是数列{}n a 的前n 项和,21(n n S a n n =+-∈N *),∴当1n >时,211(1)1n n S a n --=+--,……………………2分∴1121n n n n S S a a n ---=-+-,即121n n n a a a n -=-+-,……………………4分∴121n a n -=-(1)n >,即21n a n =+()n N *∈.……………………6分 (Ⅱ)∵0m >,n a n b m =,∴21n n b m +=.……………………7分∴当1m =时,1n b =,∴12n n T b b b n =+++=.……………………9分当1m ≠时,数列{}n b 是首项31b m =,公比为2q m =的等比数列, ∴3212(1)[1()]11n n n b q m m T q m--==--,……………………11分2 ∴322(1),(1)(0,1).1n n n m T m m m m m=⎧⎪=⎨->≠⎪-⎩……………………12分 18.(本题满分12分)本题主要考查三角函数的性质,三角形面积公式,向量内积的定义,余弦定理,三角函数的图象,转化化归思想、函数方程思想和数形结合思想.解:(Ⅰ)∵cos AB AC bc A ⋅=23ABC AC S ∆⋅==1cos 2sin 32A bc A =⨯=+……………………2分∴tan A =……………………3分∵0A π<<,∴3A π=.……………………4分∵2b =,∴122c ===⨯,……………………5分 在ABC ∆中,由余弦定理得,222212cos 1)41)262a b c bc A =+-=+-⨯⨯=∴a =……………………6分(Ⅱ)∵22121()sin()cos()22f x x x a aππ=++-,a =∴11()sin()cos()2326f x x x ππ=++- 11sin()cos()2362x x ππ=++- 12sin()23x π=+.……………………9分 或11()sin()cos()2326f x x x ππ=++- 1111sin cos cos sin cos cos sin sin 23232626x x x x ππππ=+++ 112(sin cos cos sin )2323x x ππ=+ 12sin()23x π=+.……………………9分 ∴()f x 的周期4T π=.……………………10分∵1x 、2x 是关于x 的方程()0f x m -=的相邻两零点,3∴1x 、2x 是曲线1()2sin()23f x x π=+与直线y m =相邻两交点的横坐标, ∴12x x -的最大值是4π.……………………12分19.(本题满分12分)本题主要考查立体几何知识,空间线线关系,线面关系,面面关系,简单几何体的体积,空间想像能力,逻辑思想能力,语言表达能力.(Ⅰ)证明:设AC 与BD 相交于点O ,连结PO .…………1分∵ABCD 是正方形,∴AC BD ⊥,且点O 是线段AC 、BD 的中点.…………2分∵PB PD =,∴PO BD ⊥.……………………3分∵PE ∥AC ,∴P ,A ,C ,E 在同一平面内.……………………4分因此,PO 、AC 是平面ACEP 内的两相交直线,∴BD ⊥平面ACEP .……………………5分∵AE ⊂平面ACEP ,∴AE BD ⊥.……………………6分(Ⅱ)解:∵∥AC ,∴四边形ACEP 是平行四边形.……………………7分∵AB PA ==PC CE ==.……………………8分∵ABCD是正方形,∴PE AC ==…………………9分∴PC CE ⊥,∴PCE ∆的面积为132PCE S ∆==.……………………10分又BO =∴13P BCE B PCE PCE V V S BO --∆==⨯⨯=……………………12分 20.(本题满分13分)本题主要考查解析几何知识,运算能力,数形结合思想,函数方程思想,逻辑思维能力,推理论证能力.解:(I)∵直线422+=x y 与圆222)(b b y x =-+)0(>b 相切, ∴b b =++-1)22(42,解得1=b .……………………2分∴椭圆的方程是1222=+y x ,………………3分 圆的方程是22(1)1x y +-=.………………4分4(II)由(I)知l :1+=kx y ,∴原点O 到直线l 的距离为112+=k d .……………6分 ∴11212+=⋅=∆k d DE S ODE .……………………7分 设),(00y x A ,由方程组⎩⎨⎧=-++=022122y x kx y ,得20214kk x +=.……………………8分 ∴220221411k kk x k AB +⋅+=⋅+=,……………………9分 ∴22222121121412121kk k k k k d AB S OAB +=+⋅+⋅+=⋅=∆.……………………10分 ∵OD E OAB S S ∆∆=λ,∴2222)21(112112k k k k +-=++⋅=λ,……………………11分 由条件,当0=k 时,A 、B 重合,不合题意,∴10<<λ,……………………12分所以λ的取值范围是)1,0(.……………………13分21.(本题满分14分)本题主要考查函数的性质,利用求导研究函数单调性的方法,分类讨论思想,函数方程思想,转化化归思想,数形结合思想.解:(Ⅰ)∵2213()(2)ln 24f x x x x ax x =-+-, ∴()f x 的定义域是(0,)+∞,()(1)ln 1f x x x a x '=-+--.……………………1分∵1x =是()f x 的一个极值点,∴(1)110f a '=--=,∴2a =.…………3分∴()(1)(ln 1)f x x x '=--.……………………4分∴当(0,1)x ∈时,()0f x '>,()f x 单调递增.当(1,)x e ∈时,()0f x '<,()f x 单调递减.当(,)x e ∈+∞时,()0f x '>,()f x 单调递增.……………………5分所以函数()f x 的单调增区间是(0,1]、[,)e +∞,单调减区间是[1,]e .…………6分(Ⅱ)由(Ⅰ)知,2213()(2)ln 224f x x x x x x =-+-, 设22321311()()()(2)ln 22432e h x f x g x x x x x x x x ex +=-=-+--++, 则()(1)(ln 1)h x x x x e '=--+-.……………………7分5 设()ln 1k x x x e =-+-,则1()1k x x'=-,当(1,)x e ∈时,()0k x '<,()k x 在区间[1,]e 上单调递减,∴当(1,)x e ∈时,()()0k x k e >=,即()(1)(ln 1)0h x x x x e '=--+->,∴()h x 在区间[1,]e 上单调递增.……………………9分⑴当121x x e ≤<≤时,有12()()h x h x <,即1122()()()()f x g x f x g x -<-,∴1212()()()()f x f x g x g x -<-.……………………10分∵()f x 在[1,]e 上单调递减,∴12()()0f x f x ->,∴1212()()()()f x f x g x g x -<-. ……………………11分⑵当211x x e ≤<≤时,有12()()h x h x >,即1122()()()()f x g x f x g x ->-,∴2121()()()()f x f x g x g x -<-.……………………12分∵()f x 在[1,]e 上单调递减,∴21()()0f x f x ->,∴1212()()()()f x f x g x g x -<-. ……………………13分综上所述,1212,[1,]()x x e x x ∀∈≠,有1212()()()()f x f x g x g x -<-.……14分。