2001年第十三届“五羊杯”初中数学竞赛试题

求不定方程整数解有三对夫妻一同上商店买东西.男的分别姓孙、姓陈、姓金，女的分别姓李、•姓赵、姓尹。

他们每人只买一种商品，并且每人所买商品的件数正好等于那种商品的单价(元数).现在知道每一个丈夫都比他的妻子多花63元,并且孙先生所买的商品比赵女士多23件,金先生所买的商品比李女士多11件,问孙先生、陈先生、金先生的爱人各是谁？例1．若b a ,都是正整数，且2001500143=+b a ，求b a +的值．(2001年北京市初中数学竞赛)例２ 设m 为正整数，且方程组⎩⎨⎧-==+17001113mx y y x ()()21 有整数解，求m 的值。

（“希望杯”数学竞赛试题）例３ 已知自然数y x ,满足789=+yx ，求y x +的值．（五羊杯数学竞赛试题） 【例1】若关于x 的方程054)15117()9)(6(2=+----x k x k k 的解都是整数，则符合条件的整数k 的值有 个．思路点拨 用因式分解法可得到根的简单表达式，因方程的类型未指明，故须按一次方程、二次方程两种情形讨论，这样确定是的值才能全面而准确．注：系数含参数的方程问题，在没有指明是二次方程时，要注意有可能是一次方程，根据问题的题设条件，看是否要分类讨论．【例2】 已知a 、b 为质数且是方程0132=+-c x x 的根，那么ba ab +的值是( ) A ．22127 B ．22125 C ．22123 D ．22121 思路点拨 由韦达定理a 、b 的关系式，结合整数性质求出a 、b 、c 的值．【例4】 当m 为整数时，关于x 的方程01)12()12(2=++--x m x m 是否有有理根?如果有，求出m 的值；如果没有，请说明理由．思路点拨 整系数方程有有理根的条件是△为完全平方数．设△=22224)12(544)12(4)12(n m m m m m =+-=+-=--+(n 为整数)解不定方程，讨论m 的存在性． 注：一元二次方程02=++c bx ax (a ≠0)而言，方程的根为整数必为有理数，而△=ac b 42-为完全平方数是方程的根为有理数的充要条件．【例5】 若关于x 的方程0)13()3(22=-+--a x a ax 至少有一个整数根，求非负整数a 的值． 思路点拨 因根的表示式复杂，从韦达定理得出的a 的两个关系式中消去a 也较困难，又因a 的次数低于x 的次数，故可将原方程变形为关于a 的一次方程．1．已知关于x 的方程012)1(2=--+-a x x a 的根都是整数，那么符合条件的整数a 有 ．2．已知方程019992=+-m x x 有两个质数解，则m ＝ ．3．给出四个命题：①整系数方程02=++c bx ax (a ≠0)中，若△为一个完全平方数，则方程必有有理根；②整系数方程02=++c bx ax (a ≠0)中，若方程有有理数根，则△为完全平方数；③无理数系数方程02=++c bx ax (a ≠0)的根只能是无理数；④若a 、b 、c 均为奇数，则方程02=++c bx ax 没有有理数根，其中真命题是 ．4．已知关于x 的一元二次方程0)12(22=+-+a x a x (a 为整数)的两个实数根是1x 、2x ，则21x x -= ． 5．设rn 为整数，且4<m<40，方程08144)32(222=+-+--m m x m x 有两个整数根，求m 的值及方程的根1.已知实数x,y,z 适合x+y=6,z 2=xy -9,则z 等于( )A.±1B.0C.1D.-12.方程组44,23.ab bc ac bc +=⎧⎨+=⎩的正整数解(a,b,c)的组数是( ) A.4 B.3 C.2 D.13.方程xy=x+y 的整数解有_____组.4.设x,y 都是正整数,且使,则y=+的最大值为________.5.求满足1116x y -=的所有正整数x,y.1.( )A.不存在B.仅有1组C.有2组D.至少有4组2.设a 、b 、c 为有理数,且等式则2a+999b+1 001c 的值是( )A.1 999B.2 000C.2 001D.2 0033.满足方程11x 2+2xy+9y 2+8x -12y+6=0的实数对(x,y)的个数等于_____.4.实数x,y 满足x ≥y ≥1和2x 2-xy -5x+y+4=0,则x+y=_________.5.a 、b 、c 都是正整数,且满足ab+bc=3 984,ac+bc=1 993,则abc•的最大值是______.6.象棋比赛共有奇数个选手参加,每位选手都同其他选手比赛一盘,记分办法是胜一盘得1分,平一盘各得0.5分,输一盘得0分,已知其中两名选手共得8分,其他人的平均分为整数,求参加此次比赛共有多少人?、。

2001年第13届“五羊杯”初中数学竞赛初二试卷一、选择题（共10小题，每小题5分，满分50分）1．（5分）化简繁分数：9876124598762378----------=----------（）A．53-B．53C．35-D．以上答案都不对2．（5分）设:3:5a b=，求下式的值：33222233222266()()44()()a b a ba b a ba b a ba b a b a b a ba b a b++-+----÷=--++--++（）A．61759261-B．12353067C．357416D．373．（5分）已知122xx-=，则以下结论中：①22154xx+=；②331118xx-=；③5515432xx+=有（）个是正确的．A．3B．2C．l D．04．（5分）方程组1(2,2)2axybx cyb c c baxycx by⎧=⎪+⎪≠≠-⎨⎪=⎪-⎩的解是（）A．22222()(2)2()(2)b cxa b cb cya b c⎧+=⎪+⎪⎨+⎪=⎪+⎩B．22222()(2)2()(2)b cxa c bb cya c b⎧+=⎪-⎪⎨+⎪=⎪-⎩C．22222()(2)2()(2)b cxa c bb cya b c⎧+=⎪-⎪⎨+⎪=⎪+⎩D．22222()(2)2()(2)b cxa b cb cya c b⎧+=⎪+⎪⎨+⎪=⎪-⎩5．（5分）下面的图形，共有（）个可以一笔画（不重复也不遗漏；下笔后笔不能离开纸）A．0B．1C．2D．36．（5分）三位数中，十位数字比百位和个位数字都要大的三位数有（）个．A．315B．240C．200D．1987．（5分）5支足球队进行循环比赛（每两支球队都赛一场），已知甲队已赛3场，乙队比甲队赛的场数多，丙队比甲队赛的场数少，丁队与戊队赛的场数一样多，但丁队与戊队没赛过．那么，总的比赛场数是（）A．8B．7C．6D．58．（5分）如图，梯形ABCD被对角线分为4个小三角形，已知AOB∆的面积分别∆和BOC 为235cm，那么梯形的面积是（）2m．25cm和2A．144B．140C．160D．无法确定9．（5分）一个平面图形，如果沿着一条直线对折能做到自身重合，便称为轴对称图形，例如正方形是轴对称图形（因为沿它的一条对角线对折，可做到自身重合）．在下图中的4 个图形中有多少个是轴对称图形（）A．4 B．3 C．2 D．110．（5分）下面算式中，每个汉字代表0，1，2，…，9中的一个数字，不同的汉字代表不同的数字．算式中的乘数应是（ ）A ．2B ．3C ．4D ．5二、填空题（共10小题，每小题5分，满分50分）11．（5分）分解因式：333(23)(32)125()x y x y x y -+---= ．12．（5分）已知222321(1)(2)12x x A Bx C x x x x +++=+++++，其中A ，B ，C 为常数，则B = ． 13．（5分）化简：22()()2()2()()()()()()()a ab ac b c a c a b a b a c b c b a c a c b ++++++=------ ． 14．（5分）若(1)(1)3x y -+=，()4xy x y -=，则77x y -= ．15．（5分）已知22673810x xy y x y c +--++是两个x ，y 的一次多项式的乘积，而c 是常数，则c = ．16．（5分）设n 是三位完全平方数，且n 的逆排数（把的数字从右到左逆排所得的数）也是完全平方数，这样的数n 共有 个．17．（5分）已知a 、b 和9的最大公约数为1，最小公倍数为72，则a b +的最大值是18．（5分）方程1433x y+=有 组正整数解． 19．（5分）一个深水井，现有5 000立方米储水量，并且地下水以每秒0.5立方米的流量涌进井内，但水井储水量达到7000立方米时便停止涌水．水井安装有往外抽水的水泵4台，每台每秒出水量0.2立方米，如果开始每天白天(7~19时）开3台水泵，晚上(197-时）开l 台水泵，3天后，改为白天开4台水泵，要使每台水泵的出水量不减少，最多能开 小时（答案四舍五入为整数）20．（5分）花城中学初二A 班的女同学计划制作200张贺年卡．如果每人做8张，任务尚未完成；如果每人做9张，则超额完成任务．后来决定增派4位男同学参加制作，任务改为300张，结果每人做了11张，超额完成了任务，那么，初二A 班女同学共有 人．。

2001年第13届“五羊杯”初中数学竞赛初三试卷一、选择题（共10小题，每小题5分，满分50分）1．（5分）方程7(1)20 7272x x++=+-的根是x=（）A．147-B．714-C．7914+-D．7914+2．（5分）设32x=-，则65331121x x x x++++=（）A．14324+B．14324-C．14332-D．32143-3．（5分）要使分式3|4|xx--有意义，则x的取值范围是（）A．12x B．12x或3x=，6，7，8，9，10 C．3x且4x≠，5，11D．3x4．（5分）如图，AOB∠的两边分别有5个点1A，2A，3A，4A，5A和4个点1B，2B，3B，4B，线段(15,14)jAiB i j之中，在AOB∠内及其边上不相交的一对线段称为“和睦线对”（不分顺序），例如54A B和43A B便是和睦线对，那么图中一共有几个“和睦线对”（）A．100B．90C．66D．605．（5分）一个木板上钉有九枚铁钉，顶尖向上（如图）用橡皮筋套住其中4枚铁钉，构成一个平行四边形，共有（）种套法．A．40B．24C．22D．216．（5分）如图，按给定的点和边，一共可以数出（ ）个多边形？A ．24B ．30C ．36D ．407．（5分）设[]x 表示不大于x 的最大整数，{}x 表示不小于x 的最小整数，x <>表示最接近x 的整数(0.5x n ≠+，n 为整数）．例如[3.4]3=，{3.4}4=， 3.43<>=．则方程3[]2{}8x x x ++<>=的解为（ ）A ．满足 1.5l x <<的全部实数B ．满足2l x <<的全部实数C ．满足.5l x l <<或1.52x <<的全部实数D ．以上答案都不对8．（5分）设[]x 表示最接近x 的整数(0.5x n ≠+，n 为整数），则[1][2][3][36]+++⋯+=（ ） A ．132B ．146C ．161D ．6669．（5分）如图，梯形ABCD 两腰DA ，CB 的延长线交于O ．已知4AOB S ∆=，9AOC S ∆=，则ABCD S =梯形（ ）A ．25B ．16.25C ．16D ．15.2510．（5分）如图，设梯形两对角线交于M ，且2AOB S c ∆=，2AMB S a ∆=，0c a >>，则ABCD S =梯形（ ）A ．242224()a c c a +B ．22224a c c a +C ．242224()a c c a -D ．22224a c c a -二、填空题（共10小题，每小题5分，满分50分）11．（5分）分解因式：42424(41)(31)10x x x x x -++++= ． 12．（5分）已知232332234a b c b c c c a b +--+++==，则2332a b ca b c-+=+- ．(0)a ≠13．（5分）不等式2243414143x x x x x x x x +-->-+---的解是 14．（5分）设2314x y -=，x ，y 都是正整数，则方程有 组正整数解．15．（5分）一个多边形一共有14条对角线，则它的内角和为 ．16．（5分）如图，是一个不规则的五角星，则A B C D E ∠+∠+∠+∠+∠= ．（用度数表示）17．（5分）把7个两两不同的球分给两个人，使得每人至少分得2个球，则不同的分法共有 种．18．（5分）如图，45AOB ∠=︒，角内有点P ，10PO =，在角的两边上有两点Q ，R （均不同于O 点），则PQR ∆的周长的最小值为 ．19．（5分）在三边长为自然数、周长不超过100、最长边与最短边之差不大于2的三角形中，互不全等的三角形共有 个．20．（5分）如图，ABC ∆的面积为S ，在BC 上有点A '，且:(0)BA A C m m ''=>；在CA 的延长线有点B '，且:(1)CB AB n n ''=>；在AB 的延长线有点C '，且:(1)AC BC k k ''=>．则A B C S'''= ．。

求二元不定方程整数解的一种方法――整除分析法我们知道：对于正整数M 、N ，若NM 是整数，则N 能整除M ，即M 是N 的整数倍． 运用这个基本常识，是我们解答求二元不定方程的整数解的一种有效方法．例1．若b a ,都是正整数，且2001500143=+b a ，求b a +的值．(2001年北京市初中数学竞赛)分析与解答：因为字母a 的系数小于字母b 的系数，于是用含有字母b 的代数式表示正整数a ．即：()143171314+--=b b a . 因为b a ,都是正整数, 所以143171+b 是整数,即c b =+143171, (1) (c 表示整数). 则c b 143171=+, 7112-+=c c b (2) 而250179311431435002001≤≤⇒≥=-b a b 故3575019209114372250179371121≤≤⇒≤-+≤c c c 所以c =1,于是代入(2)得：b =2, 将b =2, 代入(1)得：a =7，b a +=9．例２ 设m 为正整数，且方程组⎩⎨⎧-==+17001113mx y y x ()()21 有整数解，求m 的值。

（“希望杯”数学竞赛试题）分析与解答：将（2）代入（1）消去y 得关于m 和x 的二元不定方程：()7997111311⨯==+x m因为1≥m ，所以241311≥+m ，又1311799+⨯=m x 是整数， 所以237711791311或或=+m ．)(11224)(116986舍去舍去或===m m m 注意：此题利用“若N M 是整数，则N 能整除M ，即N 是M 的约数”求解。

例３ 已知自然数y x ,满足789=+y x ，求y x +的值．（五羊杯数学竞赛试题） 分析与解答： 由已知条件得：879-=y y x ，于是877297-+=y x ， 因为y x ,都是正整数,所以8772-y 是整数,即87-y 是72的正的约数， 于是87-y ＝１，２，３，４，６，８，９，１２，２４，３６，７２． 由此可求得符合要求的正整数只有2=y ，则5,3=+=y x x ．。

第十三届“五羊杯”初中数学竞赛试题初二试题(考试时间：90分钟 满分：100分)一、选择题(本大题共10小题，每小题5分，共50分，)1．化简繁分数：=8-7-6-7--3-2-8-9--5-4-6-7--2-1-8-9--( )(A)-35 (B) 35(C)-53(D)以上答案都不对2．设a ：b=3：5，求下式的值：333322222222b)-(a b)(a b)-(a -b)(a b a b -4a -b a 4b -a b -a b6a -b -a 6b a +++÷++++＝( )． (A)-92616175 (B) 30671235 (C)9157 (D)733．已知x -2x 1＝2，则以下结论中，；①54x 1x 22=+②118x 1-x 33=③5432x1x 55=+有( )个是正确的：(A)3(B)2(C)l(D)04，方程组 ⎪⎪⎩⎪⎪⎨⎧==+2by -cx axy 1cy bx axy(b≠2c ，c≠-2b)的解是( )，(A) ⎪⎪⎩⎪⎪⎨⎧++=++=c)a(2b )c 2(b y c)a(2b )c 2(b x 2222 (B) ⎪⎪⎩⎪⎪⎨⎧+=+=b)-a(2c )c 2(b y b)-a(2c )c 2(b x 2222 (C) ⎪⎪⎩⎪⎪⎨⎧++=+=)a(2b )c 2(b y b)-a(2c )c 2(b x 2222c (D) ⎪⎪⎩⎪⎪⎨⎧+=++=b)-a(2c )c 2(b y c)a(2b )c 2(b x 2222客上天然居 × 好 居然天上客 5，下面的图形中，共有( )个可以一笔画(不重复也不遗漏，下笔后笔不能离开纸)．(A)0 (B)l (C)2 (D)36，三位数中，十位数字比百位和个位数字都要大的三位数有 ( )个． (A)315 (B)240 (C)200 (D)1987．5支足球队进行循环比赛(每两支球队都赛一场)，已知甲队已赛3场，乙队比甲队赛的场数多，丙队比甲队赛的场数少，丁队与戊队赛的场数一样多，但丁队与戊队没赛过．那么，总的比赛场数是( )． (A)8 (B)7 (C)6 (D)58．如图，梯形ABCD 被对角线分为四个小三角形．已知△AOB 和△BOC 的面积分别为25m 2和35m 2，那么梯形的面积是( ) m 2．(A)144 (B)140 (C)160 (D)无法确定9．一个平面图形，如果沿着一条直线对折能做到自身重合，便称为轴对称图形，例如正方形是轴对称图形(因为沿它的一条对角线对折，可做到自身重合)．在下图中的4个图形中有( )个是轴对称图形．(A)4 (B)3 (C)2 (D)l10．下面算式中，每个汉字代表0，l ，2，……，9中的一个数字，不同的汉字代表不同的数字．算式中的乘数应是( )．(A)2 (B)3(C)4 (D)≥5二、填空题(本大题共10小题，每小题5分，共50分，)1．分解因式：(2x-3y)3+(3x-2y)3－125(x-y)3＝ ．2，已知2x CBx 1x A 2)1)(x (x 12x 3x 222++++=++++，其中A ，B ，C 为常数，则B ＝ ．3.化简：b)-a)(c -(c b)(a 2c a)-c)(b -(b a)(c 2b c)-b)(a -(a c)b)(a a(a 22++++++=4．若(x-1)(y+1)＝3，xy(x-y)＝4，则x 7-y 7＝ ．5．已知6x 2+7xy-3y 2-8x+10y+c 是两个x ，y 的一次多项式的乘积，而c 是常数，则c ＝6．设n 是三位完全平方数，且n 的逆排数(把的数字从右到左逆排所得的数)也是完全平方数，这样的数n 共有 个．7．已知a 、b 和9的最大公约数为1，最小公倍数为72，则a+b 的最大值是 8．方程y143x +＝3有 组正整数解．9．一个深水井，现有5 000立方米储水量，并且地下水以每秒0．5立方米的流量涌进井内，但水井储水量达到7000立方米时便停止涌水．水井安装有往外抽水的水泵4台，每台每秒出水量0．2立方米，如果开始每天白天(7～19时)开3台水泵，晚上(19—7时)开l 台水泵，3天后，改为白天开4台水泵，要使每台水泵的出水量不减少，最多能开小时?(答案四舍五入为整数)10．花城中学初22(A)班的女同学计划制作200张贺年卡．如果每人做8张，任务尚未完成；如果每人做9张，则超额完成任务．后来决定增派4位男同学参加制作，任务改为300张，结果每人做了11张，超额完成了任务，那么，初二(A)班女同学共有 人．。

第十二届“五羊杯”初中数学竞赛试题初一试题 (1)第十二届“五羊杯”初中数学竞赛试题初二试题 (4)第十二届“五羊杯”初中数学竞赛试题初三试题 (8)第十三届“五羊杯”初中数学竞赛试题初一试题 (13)第十三届“五羊杯”初中数学竞赛试题初二试题 (17)第十三届“五羊杯”初中数学竞赛试题初三试题 (21)2002年第1 4届“五羊杯”数学竞赛初一试题 (27)2002年第1 4届“五羊杯”数学竞赛初二试题 (33)2002年第1 4届“五羊杯”数学竞赛初三试题 (39)2003年第15届“五羊杯”初中数学竞赛初一试题 (43)2003年第15届“五羊杯”初中数学竞赛初二试题 (47)2003年第15届“五羊杯”初中数学竞赛初三试题 (51)2004年第16届“五羊杯”初中数学竞赛初三试题 (57)第十二届“五羊杯”初中数学竞赛试题初一试题(考试时间：90分钟满分：100分)一、选择题(4选l型，选对得5分，否则得0分，本大题满分50分，)1，已知68 9□□□20 312≈690亿(四舍五入)，那么其中的三位数□□□有( )种填写的方法．(A)1 000 (B)999 (C)500 (D)4992，8 642 097 53l，6 420 875 319，4 208 653 197，2 086 43l 975，864 219 753的平均数是( )．(A)4 444 455 555 (B)5 555 544 444(C)4 999 999 995 (D)5 999 999 9943．图中一共能数出( )个长方形(正方形也算作长方形)。

(A)64 (B)63 (C)60 (D)484．五羊牌电视机连续两次降价20％后，又再降价10％，或者连续两次降价25％，则前者的售价比后者的售价( )，(A)少2％ (B)不多也不少 (C)多5％ (D)多2．4％5．甲、乙两人在长400米的直路上来回慢跑，速度分别为3米/秒和2．5米/秒。

一、选择题（每题5分，共50分）1. 下列各数中，能被3整除的是：A. 12345B. 12346C. 12347D. 123482. 若a²+b²=25，且a+b=5，则a-b的值为：A. 2B. 3C. 4D. 53. 在△ABC中，∠A=60°，∠B=45°，则∠C的度数是：A. 45°B. 60°C. 75°D. 90°4. 已知等差数列{an}中，a1=2，d=3，则a10的值为：A. 25B. 28C. 31D. 345. 一个正方体的体积是64立方厘米，那么它的对角线长是：A. 4厘米B. 6厘米C. 8厘米D. 10厘米6. 下列函数中，是奇函数的是：A. y=x²B. y=x³C. y=xD. y=x²+17. 若log₂x=3，则x的值为：A. 2B. 4C. 8D. 168. 已知二次方程x²-5x+6=0的两个根分别为a和b，则a²+b²的值为：A. 14B. 15C. 16D. 179. 在等比数列{an}中，a1=2，公比q=3，则a5的值为：A. 18B. 24C. 36D. 4810. 下列命题中，正确的是：A. 若a>b，则a²>b²B. 若a²=b²，则a=bC. 若a²+b²=0，则a=0且b=0D. 若a²+b²=1，则a和b一定是单位圆上的点二、填空题（每题5分，共50分）11. 若x²-4x+3=0，则x的值为______。

12. 在△ABC中，若∠A=90°，AB=3，AC=4，则BC的长度为______。

13. 等差数列{an}的前n项和为Sn，若a1=1，d=2，则S10=______。

14. 若log₃x=2，则x的值为______。

2001年全国初中数学联赛一、选择题（每小题7分，共42分）1、a ，b ，c 为有理数，且等式62532+=++c b a 成立，则2a +999b +1001c 的值是（ ）（A ） 1999（B ）2000（C ）2001（D ）不能确定2、若1≠ab ，且有5a 2+2001a +9=0及05200192=++b b ，则ba 的值是（ ） （A ）59（B ）95（C ）52001-（D ）92001- 3、已知在△ABC 中，∠ACB =900，∠ABC =150，BC =1，则AC 的长为（ ）（A ）32+（B ）32-（C ）30⋅（D ）23-4、如图，在△ABC 中，D 是边AC 上的一点，下面四种情况中，△ABD ∽△ACB 不一定成立的情况是（ ）（A ）BD AB BC AD •=• （B ）AC AD AB •=2（C ）∠ABD =∠ACB （D ）BD AC BC AB •=•5、①在实数范围内，一元二次方程02=++c bx ax 的根为aac b b x 242-±-=；②在△ABC 中，若222AB BC AC >+，则△ABC 是锐角三角形；③在△ABC 和111C B A ∆中，a ，b ，c 分别为△ABC 的三边，111,,c b a 分别为111C B A ∆的三边，若111,,c c b b a a >>>，则△ABC 的面积S 大于111C B A ∆的面积1S 。

以上三个命题中，假命题的个数是（ ）（A ）0（B ）1（C ）2（D ）36、某商场对顾客实行优惠，规定：①如一次购物不超过200元，则不予折扣；②如一次购物超过200元但不超过500元的，按标价给予九折优惠；③如一次购物超过500元的，其中500元按第②条给予优惠，超过500元的部分则给予八折优惠。

某人两次去购物，分别付款168元和423元；如果他只去一次购物同样的商品，则应付款是（ ）（A ）522.8元（B ）510.4元（C ）560.4元（D ）472.8二、填空题（每小题7分，共28分）1、已知点P 在直角坐标系中的坐标为（0，1），O 为坐标原点，∠QPO =1500，且P 到Q 的距离为2，则Q 的坐标为 。

一、选择题（每题5分，共25分）1. 下列哪个数是偶数？A. 7B. 12C. 15D. 202. 如果一个长方形的长是6厘米，宽是3厘米，那么它的面积是多少平方厘米？A. 9B. 18C. 12D. 363. 小明有5个苹果，小华有7个苹果，他们一共有多少个苹果？A. 12B. 13C. 14D. 154. 下列哪个分数大于1/2？A. 1/3B. 2/3C. 3/4D. 4/55. 小明骑自行车去图书馆，他每小时可以骑行10公里。

如果他要去一个距离图书馆20公里的地方，他需要多长时间才能到达？A. 1小时B. 2小时C. 3小时D. 4小时二、填空题（每题5分，共25分）6. 一个正方形的周长是24厘米，那么它的面积是______平方厘米。

7. 如果x + y = 10，且x - y = 2，那么x的值是______。

8. 下列哪个数是负数？A. -5B. 0C. 5D. -39. 一个圆的半径是5厘米，那么它的直径是______厘米。

10. 小华有12个橙子，他每天吃掉3个，那么他需要______天才能吃完所有的橙子。

三、解答题（每题10分，共30分）11. 解方程：2x - 5 = 3x + 1。

12. 小明有一块长方形的地砖，长是4米，宽是2米。

他想要用这些地砖铺成一个长方形的花坛，长是8米，宽是4米。

他需要多少块这样的地砖？13. 一个数加上它的3倍等于42，求这个数。

四、应用题（每题15分，共30分）14. 小明去书店买书，买的第一本书是32元，第二本书是45元，第三本书是60元。

书店规定满100元可以打九折，小明可以节省多少钱？15. 一个班级有男生25人，女生30人。

如果要从这个班级中选出5名学生参加数学竞赛，有多少种不同的选法？---答案一、选择题：1. B2. B3. A4. B5. B二、填空题：6. 367. 78. A9. 1010. 4三、解答题：11. x = -612. 20块13. 14四、应用题：14. 小明可以节省13元。

．若51-=+b a ，13=+b a ，则53912322+++b ab a 的值为( )．A ．92B ．32C ．54D ．0 (大连市“育英杯”竞赛题)．多项式xyz y z x y z x x z z y y x 2222222-++-+-因式分解后的结果是( )．(上海市竞赛题)A ．(y －z)(x+y)(x －z)B ．(y －z)(x －y)(x ＋z)C ．(y+z)(x 一y)(x+z)D ．(y 十z)(x+y)(x 一z)．将多项式3224--x x 分解因式，结果正确的是（ ）．(2001年北京中考题)A ．)1)(3(22-+x xB ．)3)(1(22-+x xC ．)1)(1)(3(2+-+x x xD ．)3)(3)(1(2+-+x x x．下列各式分解因式后，可表示为一次因式乘积的是( )．A ．2727923-+-x x xB ．272723-+-x x xC ．272734-+-x x xD ．279323-+-x x x(第13届“希望杯”邀请赛试题)．下列5个多项式：①12222---b a b a ；②322327279a xa ax x -+-；③b d c c b d y d c b x 222)()(-+-----+；④)(6)(3m n n n m m -+- ；⑤x x 4)2(2+-其中在有理数范围内可以进行因式分解的有（ ）．A ．①、②、③B ．②、③ 、④C ．①③ 、④、⑤D ．①、②、④．613223+-+x x x 的因式是( )A ．12-xB ．2+xC ．3-xD ．12+xE ．12+x．已知c b a >>，M=a c c b b a 222++，N=222ca bc ab ++，则M 与N 的大小关系是( )A ．M<NB ．M> NC ．M ＝ND ．不能确定(第13届“希望杯”邀请赛试题)二、填空题．分解因式：10)3)(4(2424+++-+x x x x = ．(第12届“五羊杯”竞赛题)．分解因式：(x 2+3x)2-2(x 2+3x)－8＝ ．．分解因式：(x 2+x+1)(x 2+x+2)－12= ．．分解因式：x 2－xy －2y 2－x －y= ．(2001年重庆市中考题)．已知二次三项式82--mx x 在整数范围内可以分解为两个一次因式的积，则整数m 的可能取值为 ． ．分解因式：12)5)(3)(1(2+++-x x x = ．．分解因式：22635y y x xy x ++++= ．．分解因式：333)()2()2(y x y x -----= ．（第15届“五羊杯”竞赛题）．在1~100之间若存在整数n ，使n x x -+2能分解为两个整系数一次式的乘积，过样的n 有 个．三、解答题．已知在ΔABC 中，010616222=++--bc ab c b a (a 、b 、c 是三角形三边的长)求证：b c a 2=+．(天津市竞赛题)(1）(x 2+4x+8)2+3x(x 2+4x+8)+2x 2；(2)(2x 2－3x+1)2一22x 2+33x －1；(3)x 4+2001x 2+2000x+2001；(4)(6x －1)(2 x －1)(3 x －1)( x －1)+x 2；(5)bc ac ab c b a 54332222+++++；(6)613622-++-+y x y xy x ．．证明：对任何整数 x 和y ，下式的值都不会等于33．x 5+3x 4y －5x 3y 2一15x 2y 3+4xy 4+12y 5． (莫斯科奥林匹克八年级试题)．把下列各式分解因式：(1)a 2(b 一c)+b 2(c －a)+c 2 (a 一b)； (2)x 2+xy －2y 2－x+7y －6．．把下列各式分解因式：(1)(x+1)(x ＋2)(x+3)(x+6)+ x 2； (天津市竞赛题) (2)1999x 2一(19992一1)x 一1999； (重庆市竞赛题)(3)(x+y －2xy)(x+y －2)＋(xy －1)2； (4)(2x －3y)3十(3x －2y)3－125(x －y)3．(第13届“五羊杯”竞赛题)．已知乘法公式：))((43223455b ab b a b a a b a b a +-+-+=+； ))((43223455b ab b a b a a b a b a ++++-=-．利用或者不利用上述公式，分解因式：12468++++x x x x (“祖冲之杯”邀请赛试题)．把下列各式分解因式：(1)22212)16)(1(a a a a a ++-++； (2)91)72)(9)(52(2---+a a a ；(湖北省黄冈市竞赛题)(3)2)1()21(2)3()1(-+-++-+++y x y x xy xy xy ； (4)4242410)13)(14(x x x x x ++++-；(5)z y xy xyz y x z x x 222232242-++--．(天津市竞赛题)。

“五羊杯”初中数学竞赛模拟试题（初一试题）（考试时间：90分钟 满分：100分）一、 选择题（4选1型，每小题选对得5分，否则得0分。

本大题满分50分）1.3003的不大于100的正约数有（ ）个A.10B.9C.8D.72.规定a b a b a ⊗=+⨯，那么(33)(1201)⊗⨯⊗=（ ）A.5353B.3535C.4242D.24243. 现对某商品降价20%促销,为了使销售金额不变,销售量要比按原价销售时增加百分之几?A.35%B.30%C.25%D.20%4. 图中一共可以能数出（ ）个平行四边形．A.60B.61C.62D.635. 甲、乙两人在周长为600米的圆形跑道上跑步，速度分别为3.2米/秒和2.8米/秒。

他们同时在同一点A 沿相反方向出发，20分钟内共相遇（ ）次．A.11B.12C.13D.146. 将5个不同的小球放到6个不同的盒子里面，则不同的放法的总数是（ ）A . 65B . 56C . 65432⨯⨯⨯⨯D . 6543254321⨯⨯⨯⨯⨯⨯⨯⨯7. 某学校在一次打靶训练中，A ，B ，C ，D 四个人的平均环数是80环，D ，E ，F 三人平均环数是85环，A ，B ，C ，E ，F 五人的平均环数是83环，则D 的环数为（）环．A ．80分 B.83分 C.85分 D.87分8. 在1,2,3，…,2011,2012中，有（）个自然数能同时被2和5整除，而且不能被7整除．A.28B.201C.173D.1709. 观察如下分数：155254353,524,533,542,551，，，⋯⋯．其中是真分数又是既约分数(最简分数)的有( )A ．15 B.14 C ．13 D ．1210. 中学生运动会羊城赛区男、女运动员比例为17：12．组委会决定增加女子艺术体操项目，这样男、女运动员比例变为21：16；后来又决定再增加男子象棋项目，于是这个比例再变为25：17．已知男子象棋运动员比女子艺术体操运动员多92人，那么一开始的运动员总人数为 ( )A ．2314 B.2435 C ．2436 D ．2559二、 填空题（每小题答对得5分，否则得0分。

第十三届“五羊杯〞初中数学竞赛试题初三试题(考试时间：90分钟 总分值：100分)一、选择题(本大题共10小题，每题5分，共50分．)1.方程2-7x 227x)(17+++=0的根是x=( ) (A)97-14 (B)914-7 (C)311497+- (D) 311497+ 2.设x ＝3-2，那么x 6+3x 5+11x 3+2x+1=( )(A)143 +24 (B)143 -24 (C)143－32 (D)32－1433．要使分式|4-x ||8-x |3-3-x 有意义，那么x 的取值范围是( ) (A)x ≥12 (B)x ≥12或x ＝3，6，7，8，9，10(C)x ≥3且x ≠4，5，11 (D)x ≥34.如图，∠AOB 的两边分别有5个点A 1，A 2，A 3，A 4，A 5和4个点B 1,B 2，B 3，B 4，线段A i B j (1≤i ≤5, 1≤j ≤4) 之中，在∠AOB 内及其边上不相交的一对线段称为“和睦线对〞(不分顺序)，例如 A 5B 4和A 4B 3便是和睦线对，那么图中一共有 ( )个“和睦线对〞(A)100 (B)90 (C)66 (D)605．一块木板上钉有9枚铁钉，钉尖向上(如图)．用橡皮筋套住其中4枚铁钉，构成一个平行四边形，共有( )种套法(A)82 (B)40 (C)22 (D)216．如图，按给定的点和边，一共可以数出( )个多边形，(A)24 (B)30 (C)36 (D)407．设 x 表示不大于x 的最大整数， x ✍表示不小于x 的最小整数, x ✍表示最接近x 的整数(x≠n+0.5，n 为整数)．例如 3.4 =3， 3.4✍=4，3.4✍=3,那么方程3 x +2 x ✍ + x ✍=8的解为( )(A)满足l<x<1.5的全部实数(B)满足l<x<2的全部实数(C)满足l<x<l.5或1.5<x<2的全部实数(D)以上答案都不对8．设[x]表示最接近x 的整数(x ≠n+0.5，n 为整数)，那么]36[]3[]2[]1[++++ =( )(A)131 (B)146 (C)161 (D)6669．如图，梯形ABCD 两腰DA ，CB 的延长线交于O ．S △AOB ＝4，S △AOC ＝9，那么S 梯形ABCD ＝( )〔A 〕25 〔B 〕16.25 〔C 〕16 〔D 〕15.2510．如图，设梯形两对角线交于 M ，且 S △AOB =c 2,S △AMB =a 2,c>a>0,那么S 梯形ABCD =( )〔A 〕22242)(4a c c a +〔B 〕22224a c c a +〔C 〕22242)(4a c c a -〔D 〕22224a c c a -二、填空题(本大题共10小题，每题5分，共50分)1．分解因式：(x 4-4x 2+1)(x 4+3x 2+1)+10x 4＝ 2． 42b 3a c 33c 2c -b 23c -2b a ++=+=+,那么2c-3b a 3c 2b -a ++= (a ≠0)． 3．不等式3-4x 2-x -1-4x x 1-4x x -34x 2x >++的解是 ． 4．设41y 3x 2=-，x ，y 都是正整数，那么方程有 组正整数解． 5．一个多边形一共有14条对角线，那么它的内角和为 ．6．上图是一个不规那么的五角星，那么∠A+∠B+∠C+∠D+∠E ＝ (用度数表示)．7．把7个两两不同的球分给两个人，使得每人至少分得2个球，那么不同的分法共有 种．8．如图，∠AOB=45°，角内有点P ，PO=10．在两边上有点Q ，R(均不同于O)，那么△ PQR 的周长的最小值为 ．9．在三边长为自然数、周长不超过100、最长边与最短边之差不大于2的三角形中，互不全等的三角形共有 个．10．如图，△ ABC 的面积为S ，在BC 上有点A ′，且BA ′：A ′C=m(m>0)；在CA 的延长线有点B ′，且CB ′：AB ′=n(n>1)；在AB 的延长线有点C ′，且AC ′，BC ′=k(k>1)．那么S △A ′B ′C ′= ．第十三届“五羊杯〞初中数学竞赛试题初三试题初三答案7．1 1 2．因为把7件彼此相异的物件分给两个人，每件物件都有2种分法，故不同的分法共有27=1 2 8种．其中，使得有一个人没有分得物件的分法有2种，使得有一个人恰好分得一件物件的分法有2 ×7=1 4种，故使得每人至少分得2件物件的分法共有1 2 8—2—1 4=112种．。

“五羊杯”初中数学竞赛初一试题一、 选择题（4选1型，每小题选对得5分，否则得0分. 本大题满分50分.）1、规定)1(1......)2()1(1)1(1*+⨯+++⨯+++⨯=b b a a a a b a ，（其中，**b ,a N N b a ∈∈<且）那么=2011*1（ ）. A.20122011 B.20112010 C.201211+ D.201111+ 2、求5011370132451413791⨯+⨯+⨯= （ ）. A.6514 B.458 C.1311 D.11759 3、某校举办数、理、化三种学科竞赛. 其中，参加数学竞赛的学生有57人，参加化学竞赛的学生有78人，参加物理竞赛的学生有66人，既参加数学竞赛又参加物理竞赛的学生有13人，既参加数学竞赛又参加化学竞赛的学生有8人，既参加化学竞赛又参加物理竞赛的学生有5人. 三种竞赛都参加的学生有3人. 则报名参加学科竞赛的学生一共有（ ）人.A.201B.175C.178D.1814、有一家商店卖苹果，14个小时内卖出了782个，其中第一个小时卖出了23个，第二个小时卖出了56个，如果测算这家商店每个小时卖出的苹果数目，则（ ）不成立.A.必有连续2个小时至少卖了118个苹果B.必有连续3个小时至少卖了176个苹果C.必有连续4个小时至少卖了235个苹果D.必有连续6个小时至少卖了353个苹果5、右图中可以数出（ ）个长方形. A. 450 B.350 C.225 D.1256、已知2008年2月1日是星期五，那么，2008年5月4日是（ ）.A.星期一B.星期五C.星期六D.星期日7、已知现在是中午12点整，那么，经过（ ）分钟后，时针与分针第一次反向（即两针夹角为0180）.A.11360 B.11270 C.13360 D.13270 8、已知下面图形经过折叠后可围成一个正方体，则所围成的正方体中，“竞”字的对面是（ ）字.A. 赛B. 学C. 数D. 理9、小陈在玩“扫雷”游戏，下图是“扫雷”游戏的一部分，规则如下：图中数字n 表示在以该数字为中心的8个方格中有n 个地雷(n=1,2,3)，笑脸表示该方格已被探明有地雷，现在还剩下A 、B 、C 、D 四个方格未被探明，其它地方为安全区，没有地雷（包括有数字的方格）。

目　录2007年第19届“五羊杯”全国初中数学竞赛试题及详解2006年第18届“五羊杯”全国初中数学竞赛试题及详解2005年第17届“五羊杯”全国初中数学竞赛试题及详解2004年第16届“五羊杯”全国初中数学竞赛试题及详解2003年第15届“五羊杯”全国初中数学竞赛试题及详解2002年第14届“五羊杯”全国初中数学竞赛试题及详解2001年第13届“五羊杯”全国初中数学竞赛试题及详解2000年第12届“五羊杯”全国初中数学竞赛试题及详解2007年第19届“五羊杯”全国初中数学竞赛试题及详解一、选择题（每小题5分，共50分）．共有（ ）个不同的质约数。

A．B．C．D．【来源】年第届“五羊杯”全国初中数学竞赛初中一年级B 【答案】将分解质因数可得，因此的不同的质约数是、、，共个。

【解析】．计算：（ ）。

A．B．C．D．【来源】年第届“五羊杯”全国初中数学竞赛初中一年级C 【答案】【解析】解法一：原式解法二：原式。

解法三：估值：原式。

故正确的答案选C。

．计算：（ ）。

A．B．C．D．【来源】年第届“五羊杯”全国初中数学竞赛初中一年级【答案】A【解析】解法一：原式；解法二：原式；解法三：原式。

故正确的答案选A。

【评注】．若，，则和的大小关系是（ ）。

A．B．C．【来源】年第届“五羊杯”全国初中数学竞赛初中一年级A【答案】解法一：设，，则，故。

【解析】解法二：。

上式分子，故。

故正确的答案选A。

．如图，，，是三边上的中点，，，相交于点，则图中面积相等的三角形（不论顺序）有（ ）对。

A．B．C．D．【来源】年第届“五羊杯”全国初中数学竞赛初中一年级D【答案】显然，图中有个三角形，只有一个（）面积为，【解析】有个（，，，，，）面积为；有个（，，）面积为；有个（，，，，，）面积为。

故正确的答案选D。

．如图，多边形相邻两边互相垂直，要求出它的周长，需要最少知道（ ）条边的边长。

A．B．C．D．【来源】年第届“五羊杯”全国初中数学竞赛初中一年级A【答案】显然只知道边、、的长度，或知道、、的长度，便可算出多边形【解析】的周长，需要知道边长的边数最少是。

1.4 因式分解◆赛点归纳因式分解是中学数学的一种重要的恒等变形，也是解决许多数学问题的重要途径和方法．在初中数学竞赛中，常用的方法除教材中介绍的提取公因式法、公式法、分组分解法外，还有十字相乘法、折（添）项法、换元法和待定系数法等．◆解题指导例1 （2001，重庆市竞赛）因式分解：4x2－4x－y2+4y－3=______．【思路探究】这是一个二次五项式，显然没有公因式可以提取，这就要用其他因式分解法，经观察可用分组分解法．如何分组呢？例2 （2001，大连市第八届“育英杯”）分解因式x（x－1）+y（y+1）－2xy•的结果是_________．【思路探究】显然没有公因式可以提取，所以必须先运用整式乘法将它展开，展开后的多项式与例1相似，故宜用分组分解法．例3 （2002，北京市竞赛）a4+4分解因式的结果是（）．A．（a2+2a－2）（a2－2a+2）B．（a2+2a－2）（a2－2a－2）C．（a2+2a+2）（a2－2a－2）D．（a2+2a+2）（a2－2a+2）【思路探究】本题不可分组，又无法直接运用公式法，但这两项都是完全平方数，因此可通过添项利用公式法分解．例4分解因式：x3－3x2+4．【思路探究】这是一个关于x的三次式，直接运用分组分解法是难以完成的，•可以先将二次项或常数项进行拆项，再进行恰当的分组分解．例5 分解因式：x2+xy－6y2+x+13y－6．【思路探究】这是二次六项式，运用分组分解法有困难．根据整式乘法可知，这个二次六项式可分解为两个一次三项式，且前三项二次项x2+xy－6y2可分解为（x+3y）（x－2y）．由此可知，这两个一次式的常数项待定，因此，可用待定系数法分解．例6 （2000，“五羊杯”，初三）分解因式：（x4+x2－4）（x4+x2+3）+10=______．【思路探究】这是一道八次多项式因式分解题，在展开它时，要有目标，即在运用整式乘法将它展开后，必须考虑下一步能否分解因式．由观察可知，这两个四次三项式结构相同，因此，将四次项与二次项的和作为一个整体展开可分解因式．【拓展题】分解因式：（x2+xy+y2）2－4xy（x2+y2）．◆探索研讨提取公因式法、公式法和分组分解法是因式分解的基本方法．对于一些较为复杂的多项式因式分解，就需用到换元法、拆（添）项法、待定系数法．请结合本节的例题，总结拆（添）项法、换元法可分别化归为哪些基本方法？待定系数法实质是化归为解什么问题？◆能力训练1．下列四个从左到右的变形中，是因式分解的是（）．A．（x+1）（x－1）=x2－1 B．（a－b）（m－n）=（b－a）（n－m）C．ab－a－b+1=（a－1）（b－1）D．m2－2m－3=m（m－2－3m）2．把多项式x2－y2－2x－4y－3因式分解之后，正确的结果是（）．A．（x+y+3）（x－y－1）B．（x+y－1）（x－y+3）C．（x+y－3）（x－y+1）D．（x+y+1）（x－y－3）3．将多项式x2－4y2－9z2－12yz分解成因式的积，结果是（）．A．（x+2y－3z）（x－2y－3z）B．（x－2y－3z）（x－2y+3z）C．（x+2y+3z）（x+2y－3z）D．（x+2y+3z）（x－2y－3z）4．下列五个多项式：①a2b2－a2－b2－1；②x3－9ax2+27a2x－27a3；③x（b+c－d）－y（d－b－c）－2c+2d－2b；④3m（m－n）+6n（n－m）；⑤（x－2）2+4x．其中在有理数范围内可以进行因式分解的有（）．A．①，②，③B．②，③，④C．③，④，⑤D．①，②，④5．已知二次三项式21x2+ax－10可分解成两个整系数的一次因式的积，那么（）．A．a一定是奇数B．a一定是偶数C．a可为奇数也可为偶数D．a一定是负数6．将a4+b4+c4－2a2b2－2b2c2－2c2a2分解因式得（）．A．（a2－b2－c2）2B．（a2－b2－c2+2bc）（a2－b2－c2－2bc）C．（a+b－c）（a－b+c）（a+b+c）（a－b－c）D．（a+b－c）（b+c－a）（c+a－b）（a+b+c）7．分解因式3a2－7a－6=______．8．分解因式x2+4xy－4+4y2=_______．9．把代数式（x+y－2xy）（x+y－2）+（xy－1）2分解成因式的乘积，应当是______．10．分解因式（x2－1）（x+3）（x+5）+12=_______．11．分解因式x5+x+1=_______，x5+x－1=______．12．（2000，“五羊杯”，初二）分解因式（x－2）3－（y－2）3－（x－y）3．13．（2001，“五羊杯”，初二）分解因式（2x－3y）3+（3x－2y）3－125（x－y）3．14．（2002，“五羊杯”，初二）分解因式（1－7t－7t2－3t3）（1－2t－2t2－t3）－（t+1）6．15．分解因式（x+1）4+（x+3）4－272．16．分解因式6x2－5xy－6y2－2xz－23yz－20z2．答案:解题指导例1 （2x+y－3）（2x－y+1）．[提示：4x2－4x－y2+4y－3 =（4x2－4x+1）－（y2－4y+4）=（2x－1）2－（y－2）2=（2x+y－3）（2x－y+1）．]例2 （x－y）（x－y－1）．[提示：x（x－1）+y（y+1）－2xy =x2－x+y2+y－2xy=（x－y）2－（x－y）=（x－y）（x－y－1）．]例3 D [提示：a4+4=a4+4a2+4－4a2=（a2+2）2－（2a）2 =（a2+2a+2）（a2－2a+2）．]例4 （x+1）（x－2）2．解法1 x3－3x2+4=x3+x2－4x2+4=x2（x+1）－4（x+1）（x－1）=（x+1）（x－2）2．解法2 x3－3x2+4=x3+1－3x2+3=（x+1）（x2－x+1）－3（x+1）（x－1）=（x+1）（x2－4x+4）=（x+1）（x－2）2．解法3 x3－3x2+4=x3+x2－4x2－4x+4x+4=x2（x+1）－4x（x+1）+4（x+1）=（x+1）（x2－4x+4）=（x+1）（x－2）2．例5 设x2+xy－6y2+x+13y－6=（x+3y+m）（x－2y+n）=x2－2xy+nx+3xy－6y2+3ny+mx－2my+mn=x2+xy－6y2+（n+m）x+（3n－2m）y+mn．比较左、右两边对应项系数，得1,2,3213, 3.6.m n m n m n mn +=⎧=-⎧⎪-=⎨⎨=⎩⎪=-⎩解得 ∴x 2+xy －6y 2+x+13y －6=（x+3y －2）（x －2y+3）．例6 （x 2+2）（x+1）（x －1）（x 2+x+1）（x 2－x+1）．[提示：（x 4+x 2－4）（x 4+x 2+3）+10=（x 4+x 2）2－（x 4+x 2）－12+10=（x 4+x 2）2－（x 4+x 2）－2=（x 4+x 2－2）（x 4+x 2+1）=（x 2+2）（x 2－1）[（x 4+2x 2+1）－x 2]=（x 2+2）（x 2－1）[（x 2+1）2－x 2]=（x 2+2）（x+1）（x －1）（x 2+x+1）（x 2－x+1）．]【拓展题】 设a=x+y ，b=xy ，则（x 2+xy+y 2）2－4xy （x 2+y 2）=[（x+y ）2－xy] 2－4xy[（x+y ）2－2xy]=（a 2－b ）2－4b （a 2－2b ）=a 4－6a 2b+9b 2=（a 2－3b ）2=（x 2+2xy+y 2－3xy ）2=（x 2－xy+y 2）2．能力训练1．C [提示：根据因式分解的概念判断．]2．D [提示：x 2－y 2－2x －4y －3=（x 2－2x+1）－（y 2+4y+4）=（x －1）2－（y+2）2=[（x －1）+（y+2）][（x －1）－（y+2）]=（x+y+1）（x －y －3）．]3．D [提示：x 2－4y 2－9z 2－12yz=x 2－（4y 2+9z 2+12yz ）=x 2－（2y+3z ）2=[x+（2y+3z ）][x －（2y+3z ）]=（x+2y+3z）（x－2y－3z）．]4．B [提示：②式=（x－3a）3；③式=x（b+c－d）+y（b+c－d）－2（b+c－d）=（b+c－d）（x+y－2）；④式=（m－n）（3m－6n）=3（m－n）（m－2n）．所以②、③、④式合乎要求．]5．A [提示：利用十字相乘法可推断．]6．C [提示：原式=a4－a2b2－2a2bc－a2c2－a2b2+2a2bc －a2c2+b4－2b2c2+c4=a4－a2（b2+2bc+c2）－a2（b2－2bc+c2）+（b2－c2）2 =a4－a2（b+c）2－a2（b－c）2+（b+c）2（b－c）2=[a2－（b+c）2][a2－（b－c）2]=（a+b+c）（a－b－c）（a+b－c）（a－b+c）．]7．（3a+2）（a－3）．8．（x+2y+2）（x+2y－2）．[提示：x2+4xy－4+4y2 =（x2+4xy+4y2）－4=（x+2y）2－4=（x+2y+2）（x+2y－2）．]9．（x－1）2（y－1）2．[提示：（x+y－2xy）（x+y－2）+（xy－1）2．=（x+y）2－2xy（x+y）－2（x+y）+4xy+x2y2－2xy+1 =（x+y）2－2（x+y）（xy+1）+（xy+1）2=（x+y－xy－1）2=（x－1）2（y－1）2．]10．（x2+4x－3）（x2+4x+1）．[提示：（x2－1）（x+3）（x+5）+12=（x+1）（x+3）（x－1）（x+5）+12=（x2+4x+3）（x2+4x－5）+12=（x2+4x）2－2（x2+4x）－15+12=（x2+4x－3）（x2+4x+1）．]11．（x3－x2+1）（x2+x+1）；（x3+x2－1）（x2－x+1）．[提示：x5+x+1=x2（x3－1）+（x2+x+1）=（x2+x+1）[x2（x－1）+1]=（x3－x2+1）（x2+x+1）；x5+x－1=x2（x3+1）－（x2－x+1）=（x2－x+1）[x2（x+1）－1]=（x3+x2－1）（x2－x+1）．] 12．（x－2）3－（y－2）3－（x－y）3=[（x－2）－（y－2）][（x－2）2+（x－2）（y－2）+（y－2）2]－（x－y）=（x－y）[（x－2）2+（x－2）（y－2）+（y－2）2－（x－y）2]=3（x－y）（xy－2y－2x+4）=3（x－2）（y－2）（x－y）．13．A3+B3+C3－3ABC=（A+B+C）（A2+B2+C2－BC－CA－AB）．若A+B+C=0，便有A3+B3+C3=3ABC．令A=2x－3y，B=3x－2y，C=5y－5x，则符合上述条件，易得A3+B3+C3=3ABC，即（2x－3y）3+（3x－2y）3－125（x－y）3=15（2x－3y）（3x－2y）（y－x）．14．设（t+1）3=x，y=2+t+t2，则原式=[（4+2t+2t2）－3（1+3t+3t2+t3）][（2+t+t2）－（1+3t+3t2+t3）]－[（t+1）3] 2=（2y－3x）（y－x）－x2=2x2－5xy+2y2=（2x－y）（x－2y）=[2（t3+3t2+3t+t）－（t2+t+2）][（t3+3t2+3t+1）－2（t2+t+2）]=（2t3+5t2+5t）（t3+t2+t－3）=t（2t2+5t+5）（t－1）（t2+2t+3）．15．令y=(1)(3)2x x+++=x+2，则原式=（y －1）4+（y+1）4－272=2（y 4+6y 2+1）－272=2（y 4+6y 2－135）=2（y 2－9）（y 2+15）=2（y+3）（y －3）（y 2+15）=2（x+5）（x －1）（x 2+4x+19）．16．5-422-33由上面的双十字相乘法，得2×5－3×（－4）=10－12=－2．∴6x 2－5xy －6y 2－2xz －23yz －20z 2=（2x －3y －4z ）（3x+2y+5z ）．。

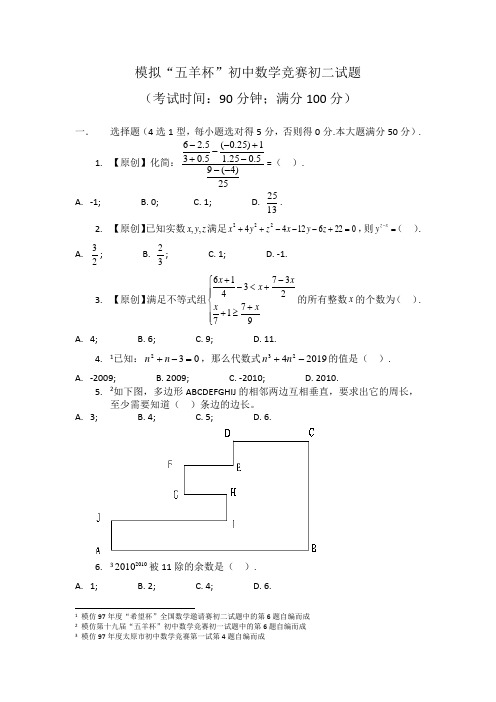
模拟“五羊杯”初中数学竞赛初二试题（考试时间：90分钟；满分100分）一． 选择题（4选1型，每小题选对得5分，否则得0分.本大题满分50分）.1. 【原创】化简：25)4(95.025.11)25.0(5.035.26---+--+-=（ ）. A. -1; B. 0; C. 1; D. 1325. 2. 【原创】已知实数z y x ,,满足022********=+---++z y x z y x ，则=-x z y （ ）.A. 23;B. 32; C. 1; D. -1. 3. 【原创】满足不等式组⎪⎪⎩⎪⎪⎨⎧+≥+-+<-+97172373416x x x x x 的所有整数x 的个数为（ ）. A. 4; B. 6; C. 9; D. 11.4. 1已知：032=-+n n ，那么代数式2019423-+n n 的值是（ ）.A. -2009;B. 2009;C. -2010;D. 2010.5. 2如下图，多边形ABCDEFGHIJ 的相邻两边互相垂直，要求出它的周长，至少需要知道（ ）条边的边长。

A. 3;B. 4;C. 5;D. 6.6. 320102010被11除的余数是（ ）.A. 1;B. 2;C. 4;D. 6. 1模仿97年度“希望杯”全国数学邀请赛初二试题中的第6题自编而成 2 模仿第十九届“五羊杯”初中数学竞赛初一试题中的第6题自编而成 3 模仿97年度太原市初中数学竞赛第一试第4题自编而成7. 4设1233+--=Θb a ab b a ，b a ,是任意实数，则=ΘΘΘΘΘΘΘ)11451041937833()10003100310313(（ ）. A. 3101510+⨯; B. 101015⨯; C. 310159+⨯; D. 91015⨯.8. 5如果c b a <<，z y x <<，且0,,≠z y x ，那么在四个代数式：①zc y b x a ++； ②y c z b x a ++；③z c x b y a ++；④y c x b z a ++中，哪一个的值最小？（ ） A. ①； B. ②； C. ③； D. ④.9. 6打字员小张连续打字20分钟，打了3609个字符，已测得他在第一分钟打了120个字符，在最后一分钟打了98个字符. 如果测算他每一分钟所打字符的个数，则以下结论不成立的是（ ）.A. 必有连续2分钟打了至少377个字符；B. 必有连续3分钟打了至少566个字符；C. 必有连续6分钟打了至少1131个字符；D. 必有连续9分钟打了至少1697个字符.10. 7空间中八个点（任意三点不共线）两两连线，用红绿两色染这些线段，其中点A 连出的线段都是红色的. 那么，以这八个点为顶点的三角形中，三边同色的三角形的个数至少为（ ）.A. 13；B. 14；C. 15；D. 16.二． 填空题（每小题填对得5分，否则得0分.本大题满分50分）.1. 8已知p 是质数，并且37+p 也是质数，则=-3811p _______. 2. 【原创】设9位自然数m=______________2201091xy ，m 是88的倍数，则m=_______. 3. 9某校初二三个班同学举行羽毛球混合双打表演，要求每班都派出一名男生和一名女生，规定同班的男女生不能配对.如果派出的男生分别是甲、乙、丙、丁，派出的女生分别是A 、B 、C 、D.第一场：甲和A 对丙和C ；第二场：丙和B 对甲和C ；第三场：丁和A 对乙和丙的同班女生.那么，甲、乙、丙、丁的同班女生分别是__________. 4模仿第十九届“五羊杯”初中数学竞赛初二试题中的第8题自编而成 5 改编自《数学竞赛培训教程（初中册）第38页例2 6 改编自第十二届“五羊杯”初中数学竞赛初二试题第10题 7 改编自《中学数学》2010年5月数学奥林匹克初中训练题129第6题 8 改编自96年度北京市初中数学竞赛初二试题第1题 9 模仿98年度北京市初一年级“迎春杯”数学竞赛试题填空题第1题自编而成4.10某个两位数___ab ，它的平方数的末两位数也是___ab ，那么___ab 为__________. 5. 11某校初中二年级同学中，有45人参加了数学竞赛，有40人参加了英语竞赛，有38人参加了语文竞赛，其中参加数学和英语两科的共有15人，参加英语和语文两科的共有20人，参加数学和语文两科的共有19人.已知参加竞赛的同学中有114的同学得了奖，则得奖的共有______人. 6. 12用一个正方形去盖住边长为3，4，5的直角三角形，那么正方形的边长不得少于_______.7. 13计算9997959319753175311⨯⨯⨯+⋯⋯+⨯⨯⨯+⨯⨯⨯=_________. 8. 14万人瞩目的世博会在上海开幕了。