[“五羊杯”第18届]第18届“五羊杯”初二数学竞赛试题(含答案)(含答案)

2018年全国初中数学联合竞赛试题(含解答)2018年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准。

第一试，选择题和填空题只设7分和0分两档；第二试各题，请严格按照本评分标准规定的评分档次给分，不要再增加其他中间档次。

如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数。

第一试一、选择题（本题满分42分，每小题7分）1.已知$x,y,z$满足$\frac{2355x-y}{y+2z}=\frac{x}{z-z^2}$，则$\frac{y+2z}{3x-y-z}$的值为（）A) 1.(B) $\frac{5}{3}$。

(C) $-\frac{1}{3}$。

(D) $-\frac{3}{5}$.答】B.解：由$\frac{2355x-y}{y+2z}=\frac{x}{z-z^2}$，得$5x-3y=3xz-3xz^2$，即$y=\frac{5}{3}x-\frac{3}{3}z+\frac{3}{3}xz^2$，所以$\frac{y+2z}{3x-y-z}=\frac{\frac{5}{3}x+\frac{1}{3}z}{\frac{4}{3}x-\frac{2}{3}z}=\frac{5}{3}$，故选（B）。

注：本题也可用特殊值法来判断。

2.当$x$分别取值$1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{2005},\frac{1}{2006}, \frac{1}{2007}$时，计算$\frac{1}{2007}+\frac{x}{21+x^2}$代数式的值，将所得的结果相加，其和等于（）A) $-1$。

(B) $1$。

(C) $0$。

(D) $2007$.答】C.解：$\frac{1}{2007}+\frac{x}{21+x^2}=\frac{1}{21}\left(\frac{21}{ 2007}+\frac{21x}{21+x^2}\right)=\frac{1}{21}\left(\frac{1}{1+x ^{-2}}\right)$，所以当$x=1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{2005},\frac{1}{200 6},\frac{1}{2007}$时，计算所得的代数式的值之和为$0$，故选（C）。

第18届“五羊杯”初二数学竞赛试题（考试时间：90分钟 满分：100分）一、选择题（4选1型，每小题选对得5分，否则得0分，本大题满分50分)1．化简繁分数：111123233(2)---+--+-----=（ ）．A 、25B ．25- C ．一2 D 、22．设23x y x y-=+，其中x ，y ≠0，则3333(23)(32)(42)(7)x y x y x y x y ---+--=（ ） A ．一l B ．1 C ．14134075 D ．14134075-3．已知三个方程构成的方程组2,1,122yz xyz xyzy z yz zx xy yz zx xy===+-+++恰有一组解,,x a y b z c ===，则333a b c ++=（ ） A ．一1 B ．1 C ．0 D ．174．设324(23)2(321)3a b c d a b c d +-+-+--=-++，则()()()()b c d c d a d a b a b c +-+-+-+-=（ ）A ．16B ．一24C ．30D ．05、杨城同学训练上楼梯赛跑，他每步可上2阶或3阶(但不上1阶，也不上4阶以上)．现共有16阶台阶，规定不许踏上第7阶，也不许踏上第13阶．那么杨城有( )种不同的上楼梯方法．(注：两种上楼梯方法，只要有某l 阶楼梯的上法不相同，就算作不同的方法．) A ．12 B ．14 C ．15 D ．166．求值：20063—10063一l0003—3000×2006×1006=( )．A ．2036216432B ．2000000000C ．12108216000D ．07．已知323x y -=，则23796x y xyxy y x--+-=（ ） A ．14 B ．14- C 、13- D 、138．计算33332461004246100624610082462006+++++++++++++++++++ A ．31003 B ．31004 C ．1334 D ．110009．至少有两个数字相同的3位数共有( )个 A ．280 B ．180 C ．252 D ．39610．五羊中学从初一到高三级学生中挑选“访贫问苦”志愿者，至少要选出( )名同学，才能做到，不管怎样挑选，以下六个条件至少能满足一个条件： 条件l ：初一级至少选3人； 条件2：初二级至少选4人； 条件3：初三级至少选5人； 条件4：高一级至少选8人； 条件5：高二级至少选20人； 条件6：高三级至少选6人．A ．47B ．46C ．41D ．40二、填空题(每小题答对得5分，否则得0分．本大题满分50分)11．若P 是两位的正整数，则以下等式中有可能成立的式子的个数是 ． A ．22006(34)(59)x Px x x ++=-- B 、22006(17)(118)x Px x x ++=-- C 、22006(34)(59)x Px x x --=+- D 、22006(17)(118)x Px x x --=+- E 、22006(1)(2006)x Px x x +-=-+12．分解因式2226773x xy y x y --+++=13．已知2323573(2)2(2)(2)x x A B Cx x x x ++=++----其中A ，B ，C 为常数，则2A+B+C=14．方程组4239x y x x y x ⎧++=⎪⎨++=⎪⎩的解共有 组15．假设一家旅馆共有30个房间，分别编以号码l ～30，现在要在每个房间的钥匙标上数字，为保密起见，要求数字用密码法，使服务员容易识别，而使局外人不易猜到．现在要求密码用两位数，左边的一个数字是原房号除以5所得的余数，右边的一个数字是原房号除以7所得的余数．那么标有36的钥匙所对应的原房号是 号．16、设251098109810(21)x x a x a x a x a x a --=+++++ ， 则97531a a a a a ++++=17、若2005200520042004200420042003200311,,2006200620052005200520052004200420052006P Q R =-=-=-则P ，Q ，R 的大小关系是 ．(注：写出P ，Q ，R 两两的大小关系)18、有一个正在向上匀速移动的自动扶梯，旅客A 从其顶端往下匀速行至其底端，共走了60级，B 从其底端往上匀速行至其顶端，共走了30级(扶梯行驶，两人也在梯上行走，且每次只跨l 级)，且A 的速度(即单位时间所走的级数)是B 的速度的3倍，那么自动扶梯露在外面的级数是19．分数12121212,,,,12380中共有 个分数可以化成混循环小数20．请你自己画图：画一个等边三角形，三个顶点标上A ，B ，C ．在三边BC ，CA ，AB 上取三等分点，BC 的三等分点(从B 到C 方向)是P ，Q ；CA 的三等分点(从C 到A 方向)是M ，N 、；AB 的三等分点(从A 到B 方向)是S ，T ．连结线段QM ，NS ，TP ．在六条 线段PQ ，QM ，MN ，NS ，ST ，TP 上再取三等分点，依次是P 1，P 2（从P 到Q 方向)；Q 1，Q 2（从Q 到M 方向)；M 1，M 2（从M 到N 方向)；N 1，N 2（(从N 到S 方向)；S 1，S 2（从S 到T 方向)；T 1，T 2（从T 到P 方向)．连结线段12211221,,,,S M S M TM T Q T Q ；1221122112211221,,,,;,,,,PS P S QS Q N Q N M P M P NP N T N T ．所得到的图形中，可以数得出来的三角形，共有 个．。

2018年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试一、选择题：（本题满分42分，每小题7分） 1．已知2012，b =，2c =，那么,,a b c 的大小关系是 （ ）A. a b c <<B. a c b <<C. b a c <<D.b c a << 【答】C.因为11a =，1b=110a b<<，故b a <.又2)1)c a -=-=1)，而221)30-=->1，故c a >.因此b a c <<.2．方程222334x xy y ++=的整数解(,)x y 的组数为 （ ） A ．3. B ．4. C ．5. D ．6. 【答】B.方程即22()234x y y ++=，显然x y +必须是偶数，所以可设2x y t +=，则原方程变为22217t y +=，它的整数解为2,3,t y =±⎧⎨=±⎩从而可求得原方程的整数解为(,)x y ＝(7,3)-，(1,3)，(7,3)-，(1,3)--，共4组.3．已知正方形ABCD 的边长为1，E 为BC 边的延长线上一点，CE ＝1，连接AE ，与CD 交于点F ，连接BF 并延长与线段DE 交于点G ，则BG 的长为 （ ）ABCD【答】D.过点C 作CP//BG ，交DE 于点P.因为BC ＝CE ＝1，所以CP 是△BEG 的中位线，所以P 为EG 的中点.又因为AD ＝CE ＝1，AD//CE ，所以△ADF ≌△ECF ，所以CF ＝DF ，又CP//FG ，所以FG 是△DCP 的中位线，所以G 为DP 的中点.因此DG ＝GP ＝PE ＝13DE. 连接BD ，易知∠BDC ＝∠EDC ＝45°，所以∠BDE ＝90°. 又BDBG==. 4．已知实数,a b 满足221a b +=，则44a ab b ++的最小值为 （ ）EC AA ．18-. B ．0. C ．1. D ．98. 【答】B.442222222219()2122()48a ab b a b a b ab a b ab ab ++=+-+=-+=--+.因为222||1ab a b ≤+=，所以1122ab -≤≤，从而311444ab -≤-≤，故2190()416ab ≤-≤，因此219902()488ab ≤--+≤，即44908a ab b ≤++≤.因此44a ab b ++的最小值为0，当a b ==a b ==时取得. 5．若方程22320x px p +--=的两个不相等的实数根12,x x 满足232311224()x x x x +=-+，则实数p的所有可能的值之和为 （ ）A ．0.B ．34-.C ．1-.D ．54-. 【答】 B.由一元二次方程的根与系数的关系可得122x x p +=-，1232x x p ⋅=--，所以2222121212()2464x x x x x x p p +=+-⋅=++，332212121212()[()3]2(496)x x x x x x x x p p p +=++-⋅=-++.又由232311224()x x x x +=-+得223312124()x x x x +=-+，所以2246442(496)p p p p p ++=+++，所以(43)(1)0p p p ++=，所以12330,,14p p p ==-=-. 代入检验可知：1230,4p p ==-均满足题意，31p =-不满足题意. 因此，实数p 的所有可能的值之和为12330()44p p +=+-=-.6．由1，2，3，4这四个数字组成四位数abcd （数字可重复使用），要求满足a c b d +=+.这样的四位数共有 （ ）A ．36个.B ．40个.C ．44个.D ．48个. 【答】C.根据使用的不同数字的个数分类考虑：（1）只用1个数字，组成的四位数可以是1111，2222，3333，4444，共有4个.（2）使用2个不同的数字，使用的数字有6种可能（1、2，1、3，1、4，2、3，2、4，3、4）.如果使用的数字是1、2，组成的四位数可以是1122，1221，2112，2211，共有4个；同样地，如果使用的数字是另外5种情况，组成的四位数也各有4个.因此，这样的四位数共有6×4＝24个.（3）使用3个不同的数字，只能是1、2、2、3或2、3、3、4，组成的四位数可以是1232，2123，2321，3212，2343，3234，3432，4323，共有8个.（4）使用4个不同的数字1，2，3，4，组成的四位数可以是1243，1342，2134，2431，3124，3421，4213，4312，共有8个.因此，满足要求的四位数共有4＋24＋8＋8＝44个. 二、填空题：（本题满分28分，每小题7分） 1．已知互不相等的实数,,a b c 满足111a b c t b c a+=+=+=，则t =_________． 【答】 1±.由1a t b +=得1b t a =-，代入1b t c +=得11t t a c +=-，整理得2(1)()0ct ac t a c -++-= ① 又由1c t a+=可得1ac at +=，代入①式得22()0ct at a c -+-=，即2()(1)0c a t --=，又c a ≠，所以210t -=，所以1t =±.验证可知：11,1a b c a a -==-时1t =；11,1a b c a a+=-=-+时1t =-.因此，1t =±. 2．使得521m⨯+是完全平方数的整数m 的个数为 ． 【答】 1．设2521mn ⨯+=（其中n 为正整数），则2521(1)(1)m n n n ⨯=-=+-，显然n 为奇数，设21n k =-（其中k 是正整数），则524(1)m k k ⨯=-，即252(1)m k k -⨯=-.显然1k >，此时k 和1k -互质，所以252,11,m k k -⎧=⨯⎨-=⎩或25,12,m k k -=⎧⎨-=⎩或22,15,m k k -⎧=⎨-=⎩解得5,4k m ==. 因此，满足要求的整数m 只有1个.3．在△ABC 中，已知AB ＝AC ，∠A ＝40°，P 为AB 上一点，∠ACP ＝20°，则BCAP＝ ． 【答】设D 为BC 的中点，在△ABC 外作∠CAE ＝20°，则∠BAE ＝60°. 作CE ⊥AE ，PF ⊥AE ，则易证△ACE ≌△ACD ，所以CE ＝CD ＝12BC. 又PF ＝PA sin ∠BAE ＝PA sin 60，PF ＝CE＝12BC ，因此BCAP4．已知实数,,a b c 满足1abc =-，4a b c ++=，22243131319a b c a a b b c c ++=------，则222a b c ++＝ ．【答】332. 因为22313(3)(1)(1)(1)a a a a abc a bc a a bc b c a b c --=-+=+-=--+=--，所以EB2131(1)(1)a a abc =----. 同理可得2131(1)(1)b b b a c =----，2131(1)(1)c c c a b =----. 结合22243131319a b c a a b b c c ++=------可得1114(1)(1)(1)(1)(1)(1)9b c a c a b ++=------，所以4(1)(1)(1)(1)(1)(1)9a b c a b c ---=-+-+-. 结合1abc =-，4a b c ++=，可得14ab bc ac ++=-. 因此，222233()2()2a b c a b c ab bc ac ++=++-++=.实际上，满足条件的,,a b c 可以分别为11,,422-.第二试 （A ）一、（本题满分20分）已知直角三角形的边长均为整数，周长为30，求它的外接圆的面积. 解 设直角三角形的三边长分别为,,a b c （a b c ≤<），则30a b c ++=.显然，三角形的外接圆的直径即为斜边长c ，下面先求c 的值. 由a b c ≤<及30a b c ++=得303a b c c =++<，所以10c >. 由a b c +>及30a b c ++=得302a b c c =++>，所以15c <.又因为c 为整数，所以1114c ≤≤. ……………………5分 根据勾股定理可得222a b c +=，把30c a b =--代入，化简得30()4500ab a b -++=，所以22(30)(30)450235a b --==⨯⨯， ……………………10分因为,a b 均为整数且a b ≤，所以只可能是22305,3023,a b ⎧-=⎪⎨-=⨯⎪⎩解得5,12.a b =⎧⎨=⎩……………………15分 所以，直角三角形的斜边长13c =，三角形的外接圆的面积为1694π. ……………………20分 二．（本题满分25分）如图，PA 为⊙O 的切线，PBC 为⊙O 的割线，A D ⊥OP 于点D .证明：2AD BD CD =⋅.证明：连接OA ，OB ，OC.∵OA ⊥AP ，A D ⊥OP ，∴由射影定理可得2PA PD PO =⋅，2AD PD OD =⋅. ……………………5分 又由切割线定理可得2PA PB PC =⋅，∴P B PC PD PO ⋅=⋅，∴D 、B 、C 、O 四点共圆，……………………10分∴∠PDB ＝∠PCO ＝∠OBC ＝∠ODC ，∠PBD ＝∠COD ，∴△PB D ∽△COD ， ……………………20分∴PD BD CD OD=，∴2AD PD OD BD CD =⋅=⋅. ……………………25分 三．（本题满分25分）已知抛物线216y x bx c =-++的顶点为P ，与x 轴的正半轴交于A 1(,0)x 、B 2(,0)x （12x x <）两点，与y 轴交于点C ，PA 是△ABC 的外接圆的切线.设M 3(0,)2-，若AM//BC ，求抛物线的解析式.解 易求得点P 23(3,)2b bc +，点C (0,)c .设△ABC 的外接圆的圆心为D ，则点P 和点D 都在线段AB 的垂直平分线上，设点D 的坐标为(3,)b m . 显然，12,x x 是一元二次方程2106x bx c -++=的两根，所以13x b =，23x b =+AB 的中点E 的坐标为(3,0)b ，所以AE……………………5分因为PA 为⊙D 的切线，所以PA ⊥AD ，又A E ⊥PD ，所以由射影定理可得2AE PE DE =⋅，即223)()||2b c m =+⋅，又易知0m <，所以可得6m =-. ……………………10分 又由DA ＝DC 得22DA DC =，即2222(30)()m b m c +=-+-，把6m =-代入后可解得6c =-（另一解0c =舍去）. ……………………15分又因为AM//BC ，所以OA OMOB OC =3||2|6|-=-. ……………………20分 把6c =-代入解得52b =（另一解52b =-舍去）. 因此，抛物线的解析式为215662y x x =-+-. ……………………25分第二试 （B ）一．（本题满分20分）已知直角三角形的边长均为整数，周长为60，求它的外接圆的面积. 解 设直角三角形的三边长分别为,,a b c （a b c ≤<），则60a b c ++=. 显然，三角形的外接圆的直径即为斜边长c ，下面先求c 的值.由a b c ≤<及60a b c ++=得603a b c c =++<，所以20c >.由a b c +>及60a b c ++=得602a b c c =++>，所以30c <.又因为c 为整数，所以2129c ≤≤. ……………………5分 根据勾股定理可得222a b c +=，把60c a b =--代入，化简得60()18000ab a b -++=，所以322(60)(60)1800235a b --==⨯⨯， ……………………10分因为,a b 均为整数且a b ≤，所以只可能是326025,6035,a b ⎧-=⨯⎪⎨-=⨯⎪⎩或2226025,6023,a b ⎧-=⨯⎪⎨-=⨯⎪⎩ 解得20,15,a b =⎧⎨=⎩或10,24.a b =⎧⎨=⎩……………………15分当20,15a b ==时，25c =，三角形的外接圆的面积为6254π； 当10,24a b ==时，26c =，三角形的外接圆的面积为169π. ……………………20分 二．（本题满分25分）如图，PA 为⊙O 的切线，PBC 为⊙O 的割线，A D ⊥OP 于点D ，△ADC 的外接圆与BC 的另一个交点为E.证明：∠BAE ＝∠ACB.证明：连接OA ，OB ，OC ，BD.∵OA ⊥AP ，A D ⊥OP ，∴由射影定理可得2PA PD PO =⋅，2AD PD OD =⋅. ……………………5分 又由切割线定理可得2PA PB PC =⋅，∴P B PC PD PO ⋅=⋅，∴D 、B 、C 、O 四点共圆，……………………10分∴∠PDB ＝∠PCO ＝∠OBC ＝∠ODC ，∠PBD ＝∠COD ，∴△PB D ∽△COD ， ∴PD BDCD OD=， ……………………15分∴2BD CD PD OD AD ⋅=⋅=，∴BD ADAD CD=. 又∠BDA ＝∠BDP ＋90°＝∠ODC ＋90°＝∠ADC ，∴△BDA ∽△ADC ， ……………………20分 ∴∠BAD ＝∠ACD ，∴AB 是△ADC 的外接圆的切线，∴∠BAE ＝∠ACB. ……………………25分三．（本题满分25分）题目和解答与（A ）卷第三题相同.第二试 （C ）一．（本题满分20分）题目和解答与（B ）卷第一题相同. 二．（本题满分25分）题目和解答与（B ）卷第二题相同. 三．（本题满分25分）已知抛物线216y x bx c =-++的顶点为P ，与x 轴的正半轴交于A 1(,0)x 、B 2(,0)x （12x x <）两点，与y 轴交于点C ，PA 是△ABC 的外接圆的切线.将抛物线向左平移1)个单位，得到的新抛物线与原抛物线交于点Q ，且∠QBO ＝∠OBC.求抛物线的解析式.解 抛物线的方程即2213(3)62b y x bc =--++，所以点P 23(3,)2b b c +，点C (0,)c . 设△ABC 的外接圆的圆心为D ，则点P 和点D 都在线段AB 的垂直平分线上，设点D 的坐标为(3,)b m . 显然，12,x x 是一元二次方程2106x bx c -++=的两根，所以13x b =，23x b =+AB 的中点E 的坐标为(3,0)b ，所以AE因为PA 为⊙D 的切线，所以PA ⊥AD ，又A E ⊥PD ，所以由射影定理可得2AE PE DE =⋅，即223)()||2b c m =+⋅，又易知0m <，所以可得6m =-. ……………………5分 又由DA ＝DC 得22DA DC =，即2222(30)()m b m c +=-+-，把6m =-代入后可解得6c =-（另一解0c =舍去）. ……………………10分将抛物线2213(3)662b y x b =--+-向左平移1)个单位后，得到的新抛物线为2213(324)662b y x b =--++-.易求得两抛物线的交点为Q 23(312102)2b b +-+. ……………………15分 由∠QBO ＝∠OBC 可得tan ∠QBO ＝tan ∠OBC.作QN ⊥AB ，垂足为N ，则N (312b +-，又233(x b b =+=，所以tan ∠QBO ＝QN BN2310212b +=12=111)]22==⋅. ……………………20分又tan ∠OBC ＝OCOB 1(2b ==⋅，所以111)](22b ⋅=⋅-. 解得4b =（另一解45)03b =<，舍去）.因此，抛物线的解析式为21466y x x =-+-. ……………………25分。

第18届“五羊杯”初中数学竞赛试题（初三试题 考试时间90分钟，满分100分）一、选择题（4选I 型，每小题选对得5分，否则得0分，本大题满分50分）1、关于x= ）A 、B 、C D2、已知2310a a -+=，那么2294921a a a --++=（ ）A 、3B 、5C 、D 、3、求和：10098S =++=（ ）A 、15 B C D 4、广州地铁实行分段计价（每相邻两站之间为1个区间，每3个区间为1个段），起价2元，每进入下一段加收1元．地铁一号线沿线站点依次为：广州东站（起点站），体育中心，体育西路，杨箕，东山口，烈士陵园，农讲所，公园前，西门口，陈家祠，长寿路，黄沙，芳村，花地湾，坑口，西朗（终点站）．小松、小梅、小柏、小枫四个好朋友分别住在体育中心、烈士陵园、长寿路、花地湾．他们相约搭乘地铁见面，应将见面地点选在哪一站可使四人所花费用最少。

答（ ）A 、杨箕B 、烈士陵园C 、长寿路D 、烈士陵园和长寿路之间任一站5、设ABC ∆中，边BC 上一点D 满足BC ：CD=4，边CA 上一点E 满足CA ：AE=5，边AB 上一点F 满足AB ：BF=6，那么DEF ∆的面积：ABC ∆的面积=（ ）A 、37：60B 、61：120C 、59：120D 、23：606、关于x 的含有绝对值的方程212x x --=的不同实数解共有（ ）个A 、1B 、2C 、3D 、47、设[]x 表示不小于x 的最小整数，如[][][][]3.44,44,3.84, 3.83===-=-．则下列7个结论中，不成立的结论（ ）①[]x x ≤ ②[]1x x <+ ③[]x x =只有x 为整数才成立 ④[][]22x x +=+⑤[][]22x x -=- ⑥[][]22x x = ⑦[]22x x ⎡⎤=⎢⎥⎣⎦A 、不超过3个B 、恰为4个C 、刚好为5个D 、至少有6个8、下列各式的结果中最小的是（ ）A 1B 、2CD 、0.89、设n=180180180…18099（前面共有100个180，最后两位是99），那么，n 能够被3，7，9，11和13这5个数中的（ ）个整除A 、2B 、3C 、4D 、510、定义新运算∆：(1)(2)(1)a b a a a a b ∆=+++++++-，其中b 为正整数．如果 (3)(2)13x x ∆∆=，则x=（ ）A 、1或138B 、1或0C 、138D 、1二、填空题（每小题答对得5分，否则得0分，本大题满分50分）11、计算，结果表示为循环小数：7(22.07)1445-÷=12、在实数范围内因式分解：432344x x x x +---=13、已知a =，则4325654a a a a -+-+=14、设1234128,10298,1002998,100029998,,a a a a =⨯=⨯=⨯=⨯ 又设123420S a a a a a =+++++，那么S 的各位数字和为15、设,,,a b c d 都是正整数，而且2341a b c d >>>>，则a 的最小值=16、令111111425364797100S +++++=⨯⨯⨯⨯⨯，则1398S +=17、正方形ABCD 的对角线交于点O ，把A 、B 、C 、D 这4点中的每一点都涂上红色、黄色、蓝色或绿色，点O 则涂上红色或黄色，每一点都涂一种颜色，而且线段OA ，OB ，OC ，OD ，AB ，BC ，CD ，DA 中每一条的两个端点的颜色不能相同，那么，一共有 种不同的涂色方法。

更多免费学习资源——博奥论坛 百度一下——博奥论坛第十九届“五羊杯”初中数学竞赛初二试题姓名一、选择题（4选1型，每小题选对得5分，否则得0分.本大题满分50分）1、化简繁分数()14153022122-------=---（ ） A 、1- B 、0 C 、1 D 、132、已知有理数,a b 满足()2:(2)2a b a b +-=，且320a b -≠，那么()32:(32)a b a b +-=（ ） A 、1- B 、1 C 、2 D 、33、若,a b 均为质数，且满足112089a b +=，则49b a -=（ ） A 、0 B 、2007 C 、2008 D 、20104、满足不等式组51432321232x x x x x +-⎧+≥-⎪⎪⎨+⎪<+⎪⎩得所有整数x 的个数为（ ）A 、1B 、2C 、9D 、205、用[]x 表示不大于x 的最大整数，例如[]1.71=，[]0.250=，[]3.44-=-，则满足[][]3.8 3.81x x =+的自然数x 有（ ）个A 、4B 、3C 、2D 、16、已知有理数,,a b c 满足3a b c -+=，2223a b c ++=，则333a b c ++=（ ） A 、1 B 、3 C 、6 D 、277、设n 是这样的正整数：不存在正整数,x y ，使得911x y n +=；但是对于每个大于n 的正整数m ，都存在正整数,x y ，使得911x y m +=.那么n =（ ） A 、79 B 、99 C 、100 D 、119 8、设222x y xy x y *=+++，,x y 是任意实数，则更多免费学习资源——博奥论坛 百度一下——博奥论坛 ()31343740898998999810111213⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫***-*-*-*-=⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦（ ）A 、1014102⨯-B 、101410⨯C 、914102⨯-D 、91410⨯9．方程组22222121y x x x y y ⎧=++⎪⎨=++⎪⎩共有（ ）组解 A 、1 B 、2 C 、3 D 、410、令20072009A =，n 是100个A 并列写成的800位数，那么n 除以11的余数是（ ） A 、1 B 、2 C 、4 D 、0二、填空题（每小题填对得5分，否则得0分.本大题满分50分）： 11、以下6个式子中有 个是恒等式：A.()()2213273x x x x --=-+ B 、()()2213273x x x x ++=++ C 、()()2213273x x x x --=-+ D 、 ()()2213273x x x x ++=++E 、()()2223273x y x y x xy y --=-+F 、()()2223273x y x y x xy y ++=++ 12、分解因式：2232x y x y -+-+= ； 13、已知()()237231111x x A B x x x x -+=++-+-+，其中,A B 为常数，则42A B -= ；14、由7,8,0（可以重复）组成的能被1125整除的最小的正整数是 ；15、写出3个相邻的正整数，使得其中任意2个数中较小的一个都可以被这两个数的差的平方整除.那么，这3个数可以是 （只需要填写一组3个数）16、设22222A x y x y =++-+，255B x x =-+，,x y 为正整数.若1A B =，则x 的所有可以取到的值为 ； 17、已知()()()()()32282012817222x x a a x a x a x +-=+++++++ ，则1234567a a a a a a a -+-+-+= ；18、右图中，长方形A B C D 的面积为48.,E F 分别在,BC CD 上，并且2BE FD ==，那么△AEF 的面积是；19、河水是流动的，在B点流入一个静止的湖中.游泳健将朱泳在河中顺流从A到B，再穿过湖游到C，共用1小时；而由C到B再到A，共用2小时.如果湖水是流动的，从B流向C，速度与河水速度相同，那么朱泳从A到B再到C，共用50分钟.这时，他从C到B再到A，共用小时；20、吴老师要考察两名学生小明和小刚聪明程度.他想好了一个正整数n，把n的一下两个特征都告诉了小明和小刚：①n是一个三位数；②n是完全平方数.吴老师还把n的3个数字的和s告诉了小明，另外把n的3个数字的积p告诉了小刚。

第十二届“五羊杯”初中数学竞赛试题初二试题(考试时间：90分钟 满分：100分)一、选择题(4选l 型，选对得5分，否则得0分．本大题50分．)1．化简繁分数：=3-2-1--5-4-6--( ) (A)32 (B)-32 (C)-2 (D)2 2．化简分式：=+÷++÷++222222)n m n -m ()n m 2mn -(1)n -m n m ()n m 2mn (1-1 (A)2n)(m 4mn + (B) 2n)(m 2mn + (c)0 (D)2 3．设a ≠b ，m ≠n ，a ，b ，m ，n 是已知数，则方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++1nb y n a x 1m b y m a x 的解是( )． (A)⎪⎪⎩⎪⎪⎨⎧+++=+++=b a n)m)(b (b y b a n)m)(a (a x (B) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)n)(b (a y b -a m)m)(b (a x (C) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)m)(b (b y b -a n)m)(a (a x ((D) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)m)(b (b -y b -a n)m)(a (a x 4． 已知x+y ≠0，x ≠z ，y ≠z ，且1+z)-y)(x (x yz ++z)-y)(y (x x z +=z)-z)(y -(x x y ，则必有( )．(A)x ＝0 (B)y ＝0 (C)z ＝0 (D)xyz ＝05.一共有( )个整数x 适合不等式|x-2 000|+|x|≤9 999．(A)lO 000 (B)2 000 (C)9 999 (D)8 0006．方程组⎪⎩⎪⎨⎧=+=+=+2xy z 2xz y 2yz x ，的解共有( )组．(A)l (B)2 (C)3 (D)≥47．设，2为自然数，A ＝14444n 2n +⋯+⋯位位，则( )．(A)A 为完全平方数 (B)A 为7的倍数(C)A 恰好有3个约数 (D)以上结论都不对8．设轮船在静水中的速度为v ，该船在流水(速度为u<v)中从上游A 驶往下游B ，再返回A ，所用时间为T ；假设u ＝0，即河流改为静水，该船从A 至B 再返回A ，所用时间为t.则( )．(A)T=t (B)T<t (C)T>t (D)不能确定T ，t 的大小关系9．如图，长方体ABCD —A'B'C'D ’长、宽、高分别为a ，b ，c ．用它表示一个蛋糕，横切两刀、纵切一切再立切两刀，可分成2×3×3＝18块大小不一的小长方体蛋糕，这18块小蛋糕的表面积之和为( )．(A)6(ab+bc+ca) (B)6(a+c)b+4ca(C)4(ab+bc+ca) (D)无法计算10．打字员小金连续打字14分钟，打了2 098个字符，测得她第一分钟打了112个字符，最后一分钟打了97个字符．如果测算她每一分钟所打字符的个数，则( )不成立，(A)必有连续2分钟打了至少315个字符(B)必有连续3分钟打了至少473个字符(C)必有连续4分钟打了至少630个字符(D)必有连续6分钟打了至少946个字符二、填空题(每小题填对得5分，不填、多填、少填、填错、仅部分填对均得0分．本大题满分50分．)1．分解因式：(x-2)3-(y-2)3-(x-y)3＝ ． 2．已知2222)(x C 2x B 1-x A 2)1)(x -(x 3x ++++=++，其中A ，B ，C 为常数，则A ＝ ，B ＝ ，C ＝ ，3．化简：xy -y)x -(x -x xy z zx x)y (z x xz -y yz -z)x -(y x yz x 222222++++++++= 4． 若x-y ＝l ，x 3-y 3＝4，则x 13-y 13＝ ．5. 已知x 6+4x 5+2x 4-6x 3-3x 2+2x+l ＝[f(x)]2，其中f(x)是x 的多项式，则f(x)＝ ．6．设自然数N 是完全平方数，N 至少是3位数，它的末2位数字不是00，且去掉此2位数字后，剩下的数还是完全平方数．则N 的最大值是 ．7．设自然数x>y ，x+y ＝667，x ，y 的最小公倍数为P ，最大公约数为Q ，P ＝120Q ，则x-y 的最大值为 .8．方程4x 2-2xy-12x+5y+ll ＝0有 组正整数解，9．一个油罐有进油龙头P 和出油龙头Q ．油罐空时，同时打开P 、Q ，4小时可注满油罐．油罐满时，先打开Q ，12小时后关上；接着打开P ，2小时后关上，此时油罐未满；再打开Q ，5小时后油罐恰好流空．那么P 的流量是，Q 的流量的 倍．10．如图，试把0，3，5，6，7，8，9这7个数填入图中的7个小圈，每个圈填1个数，不同的圈填不同的数．然后在两端填了x 和y 的每条边上标上|x-y|的数值，使得图中的9条边所标的数值刚好是1，2，3，4，5，6，7，8，9．(答案填在本题图中)初二答案一、1．B．2．A． 3．D．4．D．以(x+y)(x-z)(y-2)乘原式两边，化简得xyz=O．5．C．若x≥2 000，则不等式变为(x一2000)+x≤9 9 9 9，即2000≤x≤5 9 9 9．5，共有4000个整数适合；若O≤x<2000，则不等式变为(2000一x)+x≤9 9 9 9，2 000≤9 9 9 9，恒成立，又有2000个整数适合；若x<O，则不等式变为(2000-x)+(-x)≤9 99 9，即-3 99 9．5≤x< O，共有3 99 9个整数适合．合计有9 9 9 9个整数适合题设不等式． 6．B．有两组解：x=y=z=1，x=y=z=2，7．A．易见A=44···488···89(n个4，n-1个8)，记为An．则A1=49=72，A2=4489．=672，A3=444889=6672，…，An=66…6 72(n-1个6),A是完全平方数．但A2不是7的倍数．A3能被1，2 3，2 9，6 6 7等整除，不止3个约数．8．C．设A，B相距S,T/t>1．T>t．9．B．面积和=2×3×ab+2×2×ac+2×3×bc=6ab+4ac+6bc．1 O．_D．小金中间的l 2分钟打了2 09 8一ll 2—9 7=1889个字符．把这1 2分钟分别平均分成6段、4段、3段，每段2分钟、3分钟、4分钟，由1 88 9÷6：3 1 4…5，1 88 9÷4=4 7 2…1，1 889÷3=6 29…2，应用抽屉原理知(A)，(B)，(C)均成立．但1 8 8 9÷2—944…1，因此如果小金每分钟所打字符个数依次是11 2，15 8，1 5 7，1 58，1 5 7，1 58，157,l 5 8，1 5 7，1 5 8，l 5 7，1 5 7，1 5 7，9 7，则她连续6分钟最多打了3×(1 5 8+1 5 7)=94 5个字符，结论(D)不成立．二、1．3(x一2)(y一2)(z—y)．．2．4/9；5/9； -7/3 通分，分子相等，是恒等式3．0．4．5 2 1．5．±(x3+2x2-x-1)．6．1 6 8 1．设N=x2，x为自然数，N的末2位数字组成整数y，去掉此2位数字后得到整数M，M=m2，m为自然数，则1≤y≤99，x2=1OOm2+y，y=x2—100m2=(x+1Om)(x-1Om)．令x+10m=a，x-1OOm=b，则b≥l，m≥1，x=1Om+b≥11，a=x+10m≥21，我们要求x的最大值．若m≥4，则x=10m+b≥4 1，a=x+10m≥81，唯有b=1，m=4，x=41，a=81，y=81，M=1 6，N=1681．显然当m≤3时，z≤4 O，故N=1 6 81为所求最大值．10．答案如图．(此图旋转或翻折亦符合题意)把标上数值a的边称为“边a’’．则边9两端必为0，9；边8两端必为O，8；边7两端必为0，7．0必与9，8，7相邻．O不能再与其他数相邻．从而边6两端必为9，3；边5两端必为8，3．若O在圆周上，由3与8，9相邻，以及边4的两端必为9，5或7，3，便可填得上图．若O在中央，易见不能有符合要求的图形．第十三届“五羊杯”初中数学竞赛试题初二试题(考试时间：90分钟 满分：100分)一、选择题(本大题共10小题，每小题5分，共50分，)1．化简繁分数：=8-7-6-7--3-2-8-9--5-4-6-7--2-1-8-9--( ) (A)-35 (B) 35 (C)-53 (D)以上答案都不对 2．设a ：b=3：5，求下式的值：333322222222b)-(a b)(a b)-(a -b)(a b a b -4a -b a 4b -a b -a b 6a -b -a 6b a +++÷++++＝( )． (A)-92616175 (B) 30671235 (C)9157 (D) 73 3．已知x-2x 1＝2，则以下结论中，；①54x 1x 22=+②118x 1-x 33=③5432x1x 55=+ 有( )个是正确的：(A)3 (B)2 (C)l (D)04.方程组 ⎪⎪⎩⎪⎪⎨⎧==+2by-cx axy 1cy bx axy (b ≠2c ，c ≠-2b)的解是( )， (A) ⎪⎪⎩⎪⎪⎨⎧++=++=c)a(2b )c 2(b y c)a(2b )c 2(b x 2222 (B) ⎪⎪⎩⎪⎪⎨⎧+=+=b)-a(2c )c 2(b y b)-a(2c )c 2(b x 2222 (C) ⎪⎪⎩⎪⎪⎨⎧++=+=)a(2b )c 2(b y b)-a(2c )c 2(b x 2222c (D) ⎪⎪⎩⎪⎪⎨⎧+=++=b)-a(2c )c 2(b y c)a(2b )c 2(b x 22225.下面的图形中，共有( )个可以一笔画(不重复也不遗漏，下笔后笔不能离开纸)．(A)0 (B)l (C)2 (D)36.三位数中，十位数字比百位和个位数字都要大的三位数有 ( )个．(A)315 (B)240 (C)200 (D)1987．5支足球队进行循环比赛(每两支球队都赛一场)，已知甲队已赛3场，乙队比甲队赛的场数多，丙队比甲队赛的场数少，丁队与戊队赛的场数一样多，但丁队与戊队没赛过．那么，总的比赛场数是( )．(A)8 (B)7 (C)6 (D)58．如图，梯形ABCD 被对角线分为四个小三角形．已知△AOB 和△BOC 的面积分别为25m 2和35m 2，那么梯形的面积是( ) m 2．(A)144 (B)140 (C)160 (D)无法确定9．一个平面图形，如果沿着一条直线对折能做到自身重合，便称为轴对称图形，例如正方形是轴对称图形(因为沿它的一条对角线对折，可做到自身重合)．在下图中的4个图形中有( )个是轴对称图形．(A)4 (B)3 (C)2 (D)l10．下面算式中，每个汉字代表0，l ，2，……，9中的一个数字，不同的汉字代表不同的数字．算式中的乘数应是( )． (A)2 (B)3 (C)4 (D)≥5二、填空题(本大题共10小题，每小题5分，共50分，)1．分解因式：(2x-3y)3+(3x-2y)3－125(x-y)3＝ ．2.已知2x C Bx 1x A 2)1)(x (x 12x 3x 222++++=++++，其中A ，B ，C 为常数，则B ＝ ．客上天然居 × 好居然天上客3.化简：b)-a)(c -(c b)(a 2c a)-c)(b -(b a)(c 2b c)-b)(a -(a c)b)(a a(a 22++++++= . 4．若(x-1)(y+1)＝3，xy(x-y)＝4，则x 7-y 7＝ ．5．已知6x 2+7xy-3y 2-8x+10y+c 是两个x ，y 的一次多项式的乘积，而c 是常数，则c ＝6．设n 是三位完全平方数，且n 的逆排数(把的数字从右到左逆排所得的数)也是完全平方数，这样的数n 共有 个．7．已知a 、b 和9的最大公约数为1，最小公倍数为72，则a+b 的最大值是8．方程y143x +＝3有 组正整数解． 9．一个深水井，现有5 000立方米储水量，并且地下水以每秒0．5立方米的流量涌进井内，但水井储水量达到7000立方米时便停止涌水．水井安装有往外抽水的水泵4台，每台每秒出水量0．2立方米，如果开始每天白天(7～19时)开3台水泵，晚上(19—7时)开l 台水泵，3天后，改为白天开4台水泵，要使每台水泵的出水量不减少，最多能开小时?(答案四舍五入为整数)10．花城中学初22(A)班的女同学计划制作200张贺年卡．如果每人做8张，任务尚未完成；如果每人做9张，则超额完成任务．后来决定增派4位男同学参加制作，任务改为300张，结果每人做了11张，超额完成了任务，那么，初二(A)班女同学共有 人．初 二答案一、1．A ．2.C3．B ．4．C ．5．D ．6．B ．7．C ．乙队已赛过4场．若丙队只赛过1场，则丙队与甲队没赛过。

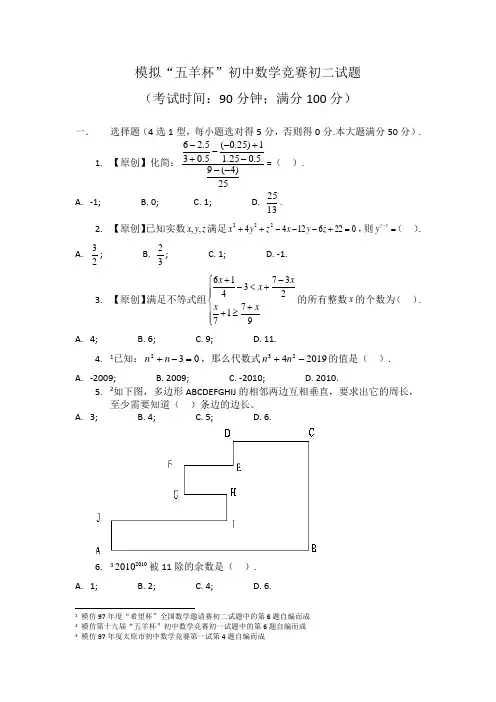
模拟“五羊杯”初中数学竞赛初二试题（考试时间：90分钟；满分100分）一． 选择题（4选1型，每小题选对得5分，否则得0分.本大题满分50分）.1. 【原创】化简：25)4(95.025.11)25.0(5.035.26---+--+-=（ ）. A. -1; B. 0; C. 1; D. 1325. 2. 【原创】已知实数z y x ,,满足022********=+---++z y x z y x ，则=-x z y （ ）.A. 23;B. 32; C. 1; D. -1. 3. 【原创】满足不等式组⎪⎪⎩⎪⎪⎨⎧+≥+-+<-+97172373416x x x x x 的所有整数x 的个数为（ ）. A. 4; B. 6; C. 9; D. 11.4. 1已知：032=-+n n ，那么代数式2019423-+n n 的值是（ ）.A. -2009;B. 2009;C. -2010;D. 2010.5. 2如下图，多边形ABCDEFGHIJ 的相邻两边互相垂直，要求出它的周长，至少需要知道（ ）条边的边长。

A. 3;B. 4;C. 5;D. 6.6. 320102010被11除的余数是（ ）.A. 1;B. 2;C. 4;D. 6. 1模仿97年度“希望杯”全国数学邀请赛初二试题中的第6题自编而成 2 模仿第十九届“五羊杯”初中数学竞赛初一试题中的第6题自编而成 3 模仿97年度太原市初中数学竞赛第一试第4题自编而成7. 4设1233+--=Θb a ab b a ，b a ,是任意实数，则=ΘΘΘΘΘΘΘ)11451041937833()10003100310313(（ ）. A. 3101510+⨯; B. 101015⨯; C. 310159+⨯; D. 91015⨯.8. 5如果c b a <<，z y x <<，且0,,≠z y x ，那么在四个代数式：①zc y b x a ++； ②y c z b x a ++；③z c x b y a ++；④y c x b z a ++中，哪一个的值最小？（ ） A. ①； B. ②； C. ③； D. ④.9. 6打字员小张连续打字20分钟，打了3609个字符，已测得他在第一分钟打了120个字符，在最后一分钟打了98个字符. 如果测算他每一分钟所打字符的个数，则以下结论不成立的是（ ）.A. 必有连续2分钟打了至少377个字符；B. 必有连续3分钟打了至少566个字符；C. 必有连续6分钟打了至少1131个字符；D. 必有连续9分钟打了至少1697个字符.10. 7空间中八个点（任意三点不共线）两两连线，用红绿两色染这些线段，其中点A 连出的线段都是红色的. 那么，以这八个点为顶点的三角形中，三边同色的三角形的个数至少为（ ）.A. 13；B. 14；C. 15；D. 16.二． 填空题（每小题填对得5分，否则得0分.本大题满分50分）.1. 8已知p 是质数，并且37+p 也是质数，则=-3811p _______. 2. 【原创】设9位自然数m=______________2201091xy ，m 是88的倍数，则m=_______. 3. 9某校初二三个班同学举行羽毛球混合双打表演，要求每班都派出一名男生和一名女生，规定同班的男女生不能配对.如果派出的男生分别是甲、乙、丙、丁，派出的女生分别是A 、B 、C 、D.第一场：甲和A 对丙和C ；第二场：丙和B 对甲和C ；第三场：丁和A 对乙和丙的同班女生.那么，甲、乙、丙、丁的同班女生分别是__________. 4模仿第十九届“五羊杯”初中数学竞赛初二试题中的第8题自编而成 5 改编自《数学竞赛培训教程（初中册）第38页例2 6 改编自第十二届“五羊杯”初中数学竞赛初二试题第10题 7 改编自《中学数学》2010年5月数学奥林匹克初中训练题129第6题 8 改编自96年度北京市初中数学竞赛初二试题第1题 9 模仿98年度北京市初一年级“迎春杯”数学竞赛试题填空题第1题自编而成4.10某个两位数___ab ，它的平方数的末两位数也是___ab ，那么___ab 为__________. 5. 11某校初中二年级同学中，有45人参加了数学竞赛，有40人参加了英语竞赛，有38人参加了语文竞赛，其中参加数学和英语两科的共有15人，参加英语和语文两科的共有20人，参加数学和语文两科的共有19人.已知参加竞赛的同学中有114的同学得了奖，则得奖的共有______人. 6. 12用一个正方形去盖住边长为3，4，5的直角三角形，那么正方形的边长不得少于_______.7. 13计算9997959319753175311⨯⨯⨯+⋯⋯+⨯⨯⨯+⨯⨯⨯=_________. 8. 14万人瞩目的世博会在上海开幕了。

第二十一届“五羊杯”初中数学竞赛初二试题（考试时间90分钟，满分100分）一、选择题（4选1型，共10小题，每小题选对得5分，否则得O 分．本题满分50分）．1．计算：（）=--+137137A ．2/23；B ．2；C ．2D ．222．己知x ，y ，z 是正整数，且222z y x =+，则下列结论正确的是( )．A ．茗是4的倍数，y 不是4的倍数；B ．x 不是4的倍数，y 是4的倍数；C ．x 和y 都不是4的倍数；D ．工和y 至少有一个是4的倍数，3．若02223=+++x x x ，则 ++--20062008x x2009200720053241x x x x x x x +++++++++-- 的值为（ ）A.1；B.0；C. -1；D.2.4．若有一个公共角的两个三角形被称为一对“共角三角形”，则图1中以角曰为公共角的“共角三角形”有( )对．A.6；B.9；C.12；D.15.5．己知三角形的三条边a ，b ，c 的长都为整数，且a ≤b ＜c ．如果b=8，则这样的三角形有( )个．A ．21；B ．28；C ．49；D ．54.6．设a ，b ，c 均为正数，若a cbc b a b a c +<+<+则a ，b ，c 三个数的大小关系是( )． A ．c ＜a ＜b ； B ．b ＜c ＜a ； C ．a ＜b ＜c ； D.c ＜b ＜a ．7．晚会上，工作人员在礼堂四周挂了一串彩色的气球，个数超过5000个，其排列的规则如下：红黄黄蓝绿红蓝绿红黄黄蓝绿红蓝绿红黄黄蓝绿红蓝绿红黄黄……那么第2009个气球的颜色为( )．A ．红；B ．黄；C ．蓝；D ．绿．8．己知方程组⎪⎩⎪⎨⎧=+=+n x y mn x n 2720092，（其中m 是偶数，n 是奇数）有两组整数解⎩⎨⎧==⎩⎨⎧==q y p x b y a x 2211,，若令M =a+b ，N=p+q ，那么下列说法正确的是( )．A ．M ，N 中有一个是偶数，一个是奇数；B ．M ，N 两个都是偶数； C. M ，N 两个都是奇数； D ．M ，N 的奇偶性不能确定．9．假设△表示运算符号并定义a △b =axb-2b ，如果c △d =X ，d △c=Y ，e △c=Z ，且有O ＜c ＜d ＜e ，则( )．A ．X=Y ＜Z ；B ．X ＞Y ＞Z ； C.X ＜Y ＜Z ； D ．X ＞Y ，Y ＜Z10.有一摞208张的卡片，贝贝拿着它，从最上面的一张开始，按如下的顺序进行操作：把上面的第一张卡片拿掉，把下一张卡片放到这摞卡片的最下面；再把原来第三张卡片拿掉，把下一张卡片放到最下面，反复这样地做，直到手中只剩下一张卡片．那么剩下的这张卡片是原来那一摞卡片中的第( )张?A.208；B.128；C.104；D.160.二、填空题（共10小题，每小题答对得5分，否则得O 分，本题满分50分）．11.分解因式：=-+---333)()()(z y z x y x __________________________________。

2018年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试一、选择题：（本题满分42分，每小题7分）1．已知21a ，32b，62c ，那么,,a b c 的大小关系是（）A.ab cB.ac b C.bacD.b ca【答】C. 因为121a，132b，所以110ab，故ba .又(62)(21)6ca(21)，而22(6)(21)3220，所以621，故ca .因此ba c .2．方程222334x xy y的整数解(,)x y 的组数为（）A ．3.B ．4.C ．5.D ．6.【答】B. 方程即22()234xy y，显然x y 必须是偶数，所以可设2x y t ，则原方程变为22217ty，它的整数解为2,3,t y从而可求得原方程的整数解为(,)x y ＝(7,3)，(1,3)，(7,3)，(1,3)，共4组.3．已知正方形ABCD 的边长为1，E 为BC 边的延长线上一点，CE ＝1，连接AE ，与CD 交于点F ，连接BF 并延长与线段DE 交于点G ，则BG 的长为（）A ．63B ．53C ．263D ．253【答】D.过点C 作CP//BG ，交DE 于点P.因为BC ＝CE ＝1，所以CP 是△BEG 的中位线，所以P 为EG 的中点.又因为AD ＝CE ＝1，AD//CE ，所以△ADF ≌△ECF ，所以CF ＝DF ，又CP//FG ，所以FG 是△DCP 的中位线，所以G 为DP 的中点.因此DG ＝GP ＝PE ＝13DE ＝23.连接BD ，易知∠BDC ＝∠EDC ＝45°，所以∠BDE ＝90°. 又BD ＝2，所以BG ＝22225BDDG293.4．已知实数,a b 满足221a b ，则44a ab b 的最小值为（）PGFEBCADA ．18. B ．0. C ．1. D ．98.【答】B.442222222219()2122()48aabbab a bab a b ab ab .因为222||1ab a b ，所以1122ab ，从而311444ab，故2190()416ab，因此219902()488ab，即44908aabb.因此44a abb 的最小值为0，当22,22a b或22,22ab时取得.5．若方程22320x pxp 的两个不相等的实数根12,x x 满足232311224()xxxx ，则实数p的所有可能的值之和为（）A ．0.B ．34. C ．1.D ．54.【答】 B.由一元二次方程的根与系数的关系可得122x x p ，1232x x p ，所以2222121212()2464x x x x x x p p，332212121212()[()3]2(496)xxx x x x x x p pp.又由232311224()x x x x 得223312124()x x x x ，所以2246442(496)p p p pp ，所以(43)(1)0p pp ，所以12330,,14p p p .代入检验可知：1230,4p p 均满足题意，31p 不满足题意. 因此，实数p 的所有可能的值之和为12330()44p p .6．由1，2，3，4这四个数字组成四位数abcd （数字可重复使用），要求满足a cb d .这样的四位数共有（）A ．36个.B ．40个.C ．44个.D ．48个.【答】C.根据使用的不同数字的个数分类考虑：（1）只用1个数字，组成的四位数可以是1111，2222，3333，4444，共有4个.（2）使用2个不同的数字，使用的数字有6种可能（1、2，1、3，1、4，2、3，2、4，3、4）.如果使用的数字是1、2，组成的四位数可以是1122，1221，2112，2211，共有4个；同样地，如果使用的数字是另外5种情况，组成的四位数也各有4个.因此，这样的四位数共有6×4＝24个.（3）使用3个不同的数字，只能是1、2、2、3或2、3、3、4，组成的四位数可以是1232，2123，2321，3212，2343，3234，3432，4323，共有8个.（4）使用4个不同的数字1，2，3，4，组成的四位数可以是1243，1342，2134，2431，3124，3421，4213，4312，共有8个.因此，满足要求的四位数共有4＋24＋8＋8＝44个.二、填空题：（本题满分28分，每小题7分）1．已知互不相等的实数,,a b c 满足111abct b c a，则t_________．【答】1.由1a t b 得1bt a，代入1bt c得11t tac ，整理得2(1)()0ct ac ta c ①又由1c t a 可得1ac at ，代入①式得22()0ctatac ，即2()(1)0c a t，又c a ，所以210t，所以1t.验证可知：11,1a b caa时1t；11,1a bcaa时1t .因此，1t .2．使得521m是完全平方数的整数m 的个数为．【答】1．设2521mn （其中n 为正整数），则2521(1)(1)mnn n ，显然n 为奇数，设21n k （其中k 是正整数），则524(1)mk k ，即252(1)m k k .显然1k，此时k 和1k 互质，所以252,11,m k k 或25,12,m k k 或22,15,m k k 解得5,4k m .因此，满足要求的整数m 只有1个.3．在△ABC 中，已知AB ＝AC ，∠A ＝40°，P 为AB 上一点，∠ACP ＝20°，则BC AP＝．【答】3.设D 为BC 的中点，在△ABC 外作∠CAE ＝20°，则∠BAE ＝60°. 作CE ⊥AE ，PF ⊥AE ，则易证△ACE ≌△ACD ，所以CE ＝CD ＝12BC.又PF ＝PA sin ∠BAE ＝PA sin 60°＝32AP ，PF ＝CE ，所以32AP ＝12BC ，因此BC AP＝3.4．已知实数,,a b c 满足1abc，4a b c ，22243131319a b c aa bb cc ，则222abc ＝．【答】332.因为22313(3)(1)(1)(1)aa aa abc a bc a a bcbc a b c ，所以FEDBCAP2131(1)(1)a aa b c .同理可得2131(1)(1)b b b a c ，2131(1)(1)c cc a b .结合22243131319ab c aa bb cc 可得1114(1)(1)(1)(1)(1)(1)9b c a c a b ，所以4(1)(1)(1)(1)(1)(1)9a b c a b c .结合1abc，4a b c，可得14ab bc ac. 因此，222233()2()2a bca bc ab bc ac .实际上，满足条件的,,a b c 可以分别为11,,422.第二试（A)一、（本题满分20分）已知直角三角形的边长均为整数，周长为30，求它的外接圆的面积.解设直角三角形的三边长分别为,,a b c （a b c ），则30a b c .显然，三角形的外接圆的直径即为斜边长c ，下面先求c 的值.由a b c 及30a b c 得303a b c c ，所以10c . 由a b c 及30a b c 得302a b c c ，所以15c . 又因为c 为整数，所以1114c .……………………5分根据勾股定理可得222abc ，把30ca b 代入，化简得30()4500ab a b ，所以22(30)(30)450235a b ，……………………10分因为,a b 均为整数且a b ，所以只可能是22305,3023,ab解得5,12.a b ……………………15分所以，直角三角形的斜边长13c ，三角形的外接圆的面积为1694.……………………20分二．（本题满分25分）如图，PA 为⊙O 的切线，PBC 为⊙O 的割线，AD ⊥OP 于点D .证明：2ADBD CD .DPOABC2018年全国初中数学联合竞赛试题参考答案及评分标准第1页（共4页）证明：连接OA ，OB ，OC.∵OA ⊥AP ，A D ⊥OP ，∴由射影定理可得2PAPD PO ，2ADPD OD . ……………………5分又由切割线定理可得2PAPB PC ，∴PB PC PD PO ，∴D 、B 、C 、O 四点共圆，……………………10分∴∠PDB ＝∠PCO ＝∠OBC ＝∠ODC ，∠PBD ＝∠COD ，∴△PBD ∽△COD ，……………………20分∴PD BD CD OD，∴2AD PD OD BD CD .……………………25分三．（本题满分25分）已知抛物线216yxbx c 的顶点为P ，与x 轴的正半轴交于A 1(,0)x 、B 2(,0)x （12x x ）两点，与y 轴交于点C ，PA 是△ABC 的外接圆的切线.设M 3(0,)2，若AM//BC ，求抛物线的解析式.解易求得点P 23(3,)2b bc ，点C (0,)c .设△ABC 的外接圆的圆心为D ，则点P 和点D 都在线段AB 的垂直平分线上，设点D 的坐标为(3,)b m .显然，12,x x 是一元二次方程2106x bx c的两根，所以21396x b bc ，22396x bbc ，又AB 的中点E 的坐标为(3,0)b ，所以AE ＝296b c .……………………5分因为PA 为⊙D 的切线，所以PA ⊥AD ，又A E ⊥PD ，所以由射影定理可得2AEPE DE ，即2223(96)()||2bc b c m ，又易知0m，所以可得6m. ……………………10分又由DA ＝DC 得22DA DC ，即22222(96)(30)()bc mb mc ，把6m代入后可解得6c （另一解0c 舍去）.……………………15分又因为AM//BC ，所以OA OM OBOC，即223||3962|6|396b b c bbc.……………………20分把6c 代入解得52b （另一解52b舍去）. 因此，抛物线的解析式为215662y xx . ……………………25分2018年全国初中数学联合竞赛试题参考答案及评分标准第1页（共5页）精品文档强烈推荐2018年全国初中数学联合竞赛试题参考答案及评分标准第4页（共7页）精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有。

第十八届“希望杯”全国数学邀请赛初二 第二试年4月15日 上午8：30至10：30一、 选择题（本大题共10小题，每小题4分，菜40分。

）以下每题的四个选项中，仅有一个是正确的，请将正确答案的英文字母写在每题后面的圆括号内。

1、红丝带是关注艾滋病防治问题的国际性标志，人胶将红丝带剪成小段，并用别针将折叠好的红丝带加紧在胸前，如图1所示，红丝带重叠部分形成的图形是（ ）（A ）正方形 （B ）矩形 C ）菱形 （D ）梯形2、设a 、b 、C 是不为零的实数，那么||||||a b c x a b c =+-的值有（ ） （A ）3种 （B ）4种 （C ）5种 （D ）6种3、ABC ∆的边长分别是21a m =-，21b m =+，()20c m m =>，则ABC ∆是（ ） （A ）等边三角形 （B ）钝角三角形 （C ）直角三角形（D ）锐角三角形4、古人用天干和地支记序，其中天干有10个；甲乙丙丁戊己庚辛壬癸，地支有12个；子丑寅卯辰巳午未申酉戌亥，将天干的10个汉字和地支的12个汉字对应排列成如下两行； 甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸甲乙丙丁……子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥……从左向右数，第1列是甲子，第2列是乙丑，第3列是丙寅……，我国的农历纪年就是按这个顺序得来的，如公历年是农历丁亥年，那么从今年往后，农历纪年为甲亥年的那一年在公历中（ ）（A ）是， （B ）是2031年， （C ）是2043年，（D ）没有对应的年号5、实数 a 、b 、m 、n 满足a<b, -1<n<m, 若1a mb M m +=+，1a nb N n+=+， 则M 与N 的大小关系是（ ）（A ）M>N (B)M=N (C)M<N (D)无法确定的。

6、若干个正方形和等腰直角三角形拼接成如图2所示的图形，若最大的正方形的边长是7cm ，则正方形A 、B 、C 、D 的面积和是（ ）（A ）214cm （B ）242cm （C ）249cm （D ）264cm7cmDC B A7、已知关于x 的不等式组230320a x a x +>⎧⎨-≥⎩恰有3个整数解，则a 的取值范围是（ ） （A ）23≤a ≤32 (B)43≤a ≤32 (C)43＜a ≤32 (D)43≤a ＜328 、The number of intersection point of the graphs of function||k y x= and function (0)y kx k =≠ is( ) (A)0 (B)1 (C)2 (D)0 or 2.9、某医药研究所开发一种新药，成年人按规定的剂量限用，服药后每毫升血液中的含药量y （毫克）与时间t （小时）之间的函数关系近似满足如图3所示曲线，当每毫升血液中的含药量不少于0.25毫克时治疗有效，则服药一次治疗疾病有效的时间为（ ）（A ）16小时 （B ）7158小时 （C ）151516小时 （D ）17小时 图3y=m/ty=ktO t （小时)y(毫克)4321110、某公司组织员工一公园划船，报名人数不足50人，在安排乘船时发现，每只船坐6人，就剩下18人无船可乘；每只船坐10人，那么其余的船坐满后内参有一只船不空也不满，参加划船的员工共有（ ）（A ）48人 （B ）45人 （C ）44人 （D ）42人二、填空题（本大题共10小题，每小题4分，共40分）11、已知a b c ⋅⋅o 为ABC ∆三边的长，则化简|a b c -+|+2()a b c -+的结果是＿＿＿12、自从扫描隧道显微镜发明后，世界上便诞生了一间新科学，这就是“纳米技术”，已知1毫米微米，1微米纳米，那么纳米的长度用科学记数法表示为＿＿米。

2018年初中数学联赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准•第一试，选择题和填空题只设7分和0分两档；第二试各题, 请按照本评分标准规定的评分档次给分•如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数第一试(A)一、选择题：(本题满分42分，每小题7分)21.设二次函数y x 2ax 22a的图象的顶点为A，与x轴的交点为B, C •当△ ABC为等边三角形时，其边长为A. 6 .%【答】C.由题设知A( a, 弩).设B(x ,0) , C(x ,0)，二次函数的图象的对称轴与2 1 2x轴的交点为D，则BC | x1 x21X)224x x1 2又AD _3 BC，则|2所以，△ ABC的边长BC 2a22a2.a2a2(舍去)ABCD2.如图，在矩形中, BAD BD的平分线交于点，AB CAE 15 BE，则CJ ,J2 1. D. 1.3【答】D.延长AE交BC于点F，过点由已知得EBH ACB BAF30 .FADE作BC的垂线，垂足为H .AFB HEF 45 , BF ABE-、—AC设BE x，则2 HF HE x , BH W3x .2因为BF BH HF ，所以3x122x，解得x 3 1.所以BE2 3.设p,q均为大于3的素数，则使p25pq 4q为完全平方数的素数对(p, q)的个数为(A.1 . 【答】B. B.2.C.3.D.4.2 2 2设p 5 pq 4q m ( m 为自然数) (m p 2q)(m p 2q) pq .【答】C.0的整数组(x, y, z)的个数为由对称性，同样可得由于p, q 为素数，且 m p 2q p, m p 2q q ，所以 m p 2q 1 , m p 2q pq ，从而 pq 2 p 4q 1 0，即(p 4)(q 2) 9，所以(p, q)(5,11)或(7, 5).所以，满足条件的素数对 (p, q)的个数为 2.4.若实数 a, b 满足a2,2(1 a)2b(1 b)2 4a A.46 .B.64.C.82.D.128.(y @ z) @ x xy z xy yz zx xyz , (z @ x) @ yz xyyz zx xyz .所以，由已知可得x y z xy yz zx xyz0，即(x 1)( y1)(z 1)1.所以，x, y, z 为整数时，只能有以下几种情况：1, x 11, x 11, 1, 或 y11, 或 y11,或1, 1,z 1所以， 1, z 11, z 11, (x, y, z) (2,2,0)或(2,0,2)或(0,2,2)或(0,0,0)，故共有4个符合要求的整数组.1,2 ，则(p 2q)2 pq m 2 , 即(1由条件—ba)2(1b)22 22a 2 2b 2 4aba 3b 3 0,2即(a b) 2[(a b)2 4ab] (a2 b)[(a b)23ab]又 a b 2,所以 22[4 4ab] 2[43ab] 0 ,解得 ab1.所以 a 2 b 2 (ab)22ab 6 ,a 3b 3 ( a b)[( a b)23ab] 14, a 5 b 5 (a 22 3 32 2 b 2 )(a3 b 3)a 2b 2(a b) 82.5.对任意的整数x, y ，定义x@ y xxy , 则使得 (x@y) @z(y@z) @x (z@x) @yA.1 . 【答】D.B.2 .C.3 .D.4.(x @ y) @ z (x y xy) @ z (x y xy) (x yxy)z z xyyz zx xyz ,1_£ 2018 2019 B.61 •_£2020C.62•因为 M 2018133，所以 M 1~~201833 61 335.__ 1 ___ 1 __ 1 1345 ■^050 ) -2030 13^050 20 83230 ,1 83230 1185 1 所以M 1345 61 1345，故M 的整数部分为61.、填空题：（本题满分 28分，每小题7 分）1.如图，在平行四边形 ABCD 中，BC 2AB ，CE AB 于E ，F 为AD 的中点，若 AEF48， 则 B ___ •【答】84 .设BC 的中点为G ，连结FG 交CE 于H ，由题设条件知 FGCD 为菱形•由AB // FG // DC 及F 为AD 的中点，知H 为CE 的中点• 又CE AB ，所以CE FG ，所以FH 垂直平分CE ，故 DFC GFC EFG AEF 48 . 所以 B FGC 180 2 48 84 •3 115 k 3孙三k 3 4k15 26•设M A.60 • 【答】B.-，则」的整数部分是 2050 MD.63 •又 M (丽^1^^12030才(203T120324(x y ） 15，则x y 的最大值为2由X 3y 3(x42(X y )( x xy令X y k ，注又因为x 2xy15可得(x y )( X 2152 .14(x y)2xy(X3Xyy 2) 11 X y) 1「即2y )2 43y 214 0,故由①式可得k 3 _3xyk _14 k152，所以xy A FG2.若实数 X, y 满足【答】3.117)x 2于是，x, y可看作关于t的一元二次方程t 2 ktk3 1k 坐(k ) 2 4 ——4 ---------- 2 0 ,3k3 2化简得k 3 k 30 0,即(k 3)(k 2 3k 10) 0，所以0 k 3.故x y的最大值为3.3. __________________________________________________ 没有重复数字且不为5的倍数的五位数的个数为__________________________________________________________ .【答】21504.显然首位数字不能为0,末位不能为0和5.当首位数字不为5时，则首位只能选0,5之外的8个数•相应地个位数只能选除0,5及万位数之外的7 个数，千位上只能选万位和个位之外的8个数，百位上只能选剩下的7个数，十位上只能选剩下的6个数•所以，此时满足条件的五位数的个数为8 7 8 7 6 18816个•当首位数字为5时，则个位有8个数可选，依次千位有8个数可选，百位有7个数可选，十位有6个数可选•所以，此时满足条件的五位数的个数为8 8 7 6 2688个•所以，满足条件的五位数的个数为18816 2688 21504 (个).5.55222 a b c4. 已知实数a,b, c满足a b c 0 ，a be 1 ,则-abc【答】5 .21 2222 13 3 3由已知条件可得ab bc ca 2 [(a b c)2 (a2 b2 c2)] 2，a b3 c 3abc，所以a5 b55,2.2 2、/ 3 .3c (a b c )(a b c3) [a2 (b3c3) .2/3 3、b (ac )2 3 3c (a b )]3abc [a2b2 ( a b) a2 c2 ( a c ) b 2 c2 (b c)] 2 23abc (abc2 2 2 2 a c bb c a)3abc 1 abc(ab bc ca) 3abc 2abc-5c K2 abc5a b c 5所以—abc 2第一试(B)一、选择题：(本题满分42分，每小题7分)2 x21.满足(x x 1) 1的整数x的个数为A.1 .B.2C.3.【答】C.当x 220 且x2.x 1 0 时，x 2.当x2x 1 1时，x 2 或x 1.当x2x 1 1且x 2为偶数时，x 0.所以，满足条件的整数x有3个.2.已知x1,x2,x3( X1X2 x3 )为关于x的方程x 34x1 X12 x22 X32A.5 .B.6C.7 .( ) D.4 .3 X2 ( a 2) x a 0的三个实数根，则( ) D.8 .【答】A.2 方程即（x 1）（x 2x a ） 0，它的一个实数根为 1,另外两个实数根之和为 2,其中必有一根小 于1，另一根大于1，于是x 2 1, x l x 3 2，故 (x 3x )( x 3x ) 2( x x 1 ) 2( x x ) 1 5 . 3 13.已知点E , F 分别在正方ABCD 的边 CD , AD 上, CD 4CE , EFB tan ABF A. 1 . B. 3 . C. & . D. ■ 3 .2 5 2 2【答】B.FBC ，贝U 不妨设CD 4，则CE 1, DE 3.设DF x 」U AF 4 x , EF J x 29 .作BH EF 于H .因为 EFB FB C AFB :, BAF △ BAF ^△BHF ，所以 BH BA 4.由SSS SS 得四边形ABF BEF DE F BCEABCD2 1 42 - 4 2 4 (4 x) 1 2 4 x 2 9 1 2 31x 2 41,解得x 8512AF 3所以AF 4 x 5 ,tan ABF AB 5 .4.方程3 x 3 x 的实数根的个数为 （ ）A.0 .B.1 .C.2.D.3.【答】B. 90 BHF , BF 公共，所以FB令y 9 x ，则y 0 ,且x y 2 9，原方程变为它3 y 』y 2 9，解得y6，从而可得x 8或x 27 . 检验可知： x 8是增根，舍去；x 27是原方程的实数根. 所以，原方程只有1个实数根 5.设a, b, c 为三个实数，它们中任何一个数加上其余两数之积的 2017倍都等于2018，则这样的三元数组（a, b, c ）的个数为A.4 .B.5.【答】B. C.6 . D.7.由已知得,a 2017bc 2018, b2017ac 2018, c 2017ab2018，两两作差，可得(a b)(12017c) 0 , (b c)(12017a) 0 , (c a)(12017b) 0 .1由(a b)(1 2017c) 0，可得a b 或c~2017 .(1 )当a b c 时，有2017a2 a 2018 0,解得 a 1 或a 20182017(2 )当a b c 时，解得a b ___ L , c 2018 12017 2017(3)当a b时，c 1，此时有：a 1 , b 2018 1，或a 2018 1 , b 12017 2017 2017 2017 2017 故这样的三元数组(a, b, c)共有5个.3 6.已知实数a, b满足a2 33a2 5a 1, b33b25b5,则a b ()A.2 .B.3 .C.4 .D.5【答】A.有已知条件可得(a 1)32(a 1) 2 , (b 1)32(b1)2，两式相加得(a 1) 32( a 1) (b 1) 32(b 1)因式分解得(a b 2)[( a 1) 2 ( a 1)b 1) (b 1) 22] 0 . 因为2(a 1)2 (a 1)(b 1)2(b 1)2 2 [(a 1)1 2(b 1)]23 (b 1)2 2 0 ,2 4所以a b 2 0,因此 a b 2.二、填空题：(本题满分28分，每小题7分)1.已知p, q, r为素数，且pqr 整除pq qr rp 1,则p q r .【答】10 .设k p qr rp 1 1 1 1 1 由题意知k是正整数，又p, q, r 2，所以k 3，从pqr p q r pqr 2而k 1 ,即有pq qr rp 1pqr，于F是可知p, q, r互不相等.当2 p q r 时，pqr pq qr rp 1 3qr，所以q 3，故q 2 .于是2qr qr 2q 2r 1,故(q 2)(r 2) 3,所以q 2 1, r 2 3，即q 3, r 5 ,所以,(p, q, r) (2,3,5).再由p, q, r的对称性知，所有可能的数组(3,5,2),(p, q, r)共有6组，即(2,3,5) , (2,5,3) , (3,2,5), (5,2,3) , (5,3,2).于是p q r 10.2.已知两个正整数的和比它们的积小 1000,若其中较大的数是完全平方数，则较小的数为 _____________ .【答】&2 2 Q Q设这两个数为 m , n (m n)，贝U m n mn 1000，即(m 21)( n 1) 1001.又 10011001 1 143 7 91 1177 13，所以(m 21, n 1) = (1001,1)或(143, 7)或(91,11)2 2或(77,13)，验证可知只有(m 2 1, n 1) (143,7)满足条件，此时 m 2 144, n 8 .3 .已知D 是厶ABC 内一点，E 是AC 的中点，AB 6 , BC 10 , BAD BCD ,EDC ABD ，贝U DE ________ .【答】4.延长CD 至F ，使DF DC ，贝U DE // AF 且DE 丄AF ，2所以 AFD EDC ABD ，故A, F, B, D 四点共圆，于是整数对(m, n)的个数为【答】16.综合可知：符合条件的正整数对 (m, n)有 8+ 4 + 2+1 + 1 = 16 个.2 2 21)]2 4(m 2 4n 250) 0 ,整理得因为二次函数的图象在 x 轴的上方，所以 514n 49，即(m 1)(2n 1)2 .因为 m, n 为正整数，所以(m 1)(2n 1)25 .2n 1 彳5?，故 n 5. [2(m 2n4mn 2m 1 2，所以 1时, _53, 故亍223，符合条件的正整数对 (m, n)有8 个;2时, 5，故m4，符合条件的正整数对(m, n)有4个;3时, 257 ,m — 187，符合条件的正整数对(m, n)有2 个; 4时, 25 m —179，符合条件的正整数对(m, n)有1 个;5时,1125，故m 1411 ,符合条件的正整数对 (m, n)有1个.BFDBAD BCD ，所以 BF BC 10，且 BD FC ,故 FABFDB 90 .又AB 6，故 AF . 102628，所以DE 丄 AF 4 .24.已知二次函数yx 22(m 2n 1)x(m 2 4n 250)的图象在x 轴的上方，则满足条件的正第二试 （A ）、（本题满分 2 20分）设a, b, c, d 为四个不同的实数，若 a, b 为方程x 10cx 11d 0的根，c, d c d 的值. a b 2 为方程x 10ax 11b 0的根，求 解由韦达定理得 10c , 10a ，两式相加得 abed 10(a c). 2 因为a 是方程x 2 10cx 11d0的根, 2 所以a 2 10ac 11d 0 ,又 d 10a c ，所以 2a 2110a 11c10ac10分 2类似可得c 2110c 11a 10ac 0.15分①一②得（a ©（a c 121) 0 .因为a c ，所以ac 121,所以a10(a c) 1210 .20分二、（本题满分25分）如图，在扇形 OAB 中, AOB 4，点D 为OB 的中点，点E 为弧AB 上的动点，OE 与CD 的交点为F . （1 ）当四边形 （2）求 CE 90，OA 12，点 C 在 OA 上, AC分别过 由ODODEC 的面积S 最大时，求EF ； 2DE 的最小值. O, E 作CD 的垂线，垂足为 M , N .6, OC 8，得 CD 10.所以OCD S ECD-' CD (OM EN )^2 CD OE _12 10 12 60， 当OEDC 时，S 取得最大值60.此时，EF OE OF12 -（2）延长 OB 至点G，使BG因为ODOE 」， DOE OEOG2所以CE 2DECE EG故CE 2DE 的最小值为& 10.OB 6 8 10 CG36 512，连结 GC,GE .E\ M F :” h” NJ !*____G10分EOG ，所以△ ODE OEG ，所以 DE 1，故 EG 2DE . EG 220分242 82 8 10，当C, E, G 三点共线时等号成立.25分2018年初中数学联赛试题参考答案及评分标准第11页（共10页）三、（本题满分25分）求所有的正整数 m, n ，使得33 2 2m n m n(m n)22 2 2 S (m n)[(m n)3mr] m n (m n)2第二试 （B ）、 （本题满分20分）若实数a, b, c 满足(a b (a bc)(1」〕）的值.a bc解 记a bc x ， ab bc ca y ，abc111(ab c)(ab 5c b c 5a c a 5b )x[3x 212(a b c)x36(ab bc ca )]c)(11 1 ) -9，求a b 5c b c 5a c a 5b 5z ，则11 1x( x 6ax 6b x 6c ) x (9 x 236》m 3 rh m 2 n 2因为 m, n 为正整数，故可令mnm np, q 为正整数，且 (p, q) 1. S (m n)凹 P 厘(mP 2n)3 pq q 2 2P因为 S 为非负整数，所以2P I q ，又(P, q)1,故 P 1，(m n) | mn .①10分所以mn n是整数，所以（m n) | n 2，故n 22 ，即 n mn .又由m 3 n 3 m 2n 2n 3m 2n 2m 3 所以 由对称性，同理可得mm 2 (n 2 故m m) m 2n ， n . 所以20分n 代入①，得2 | m ， n 代入②，得2m 34m 4 0，即 m2.所以, 满足条件的正整数m, n 为m25分3 2 x 6(a b c)x 36(ab be ca)x 216abc 5 x 336xy 216Z ， ........................... 10分---------------- 是非负整数.(m n)竺£ ( mn )2 .m nm n2018年初中数学联赛试题参考答案及评分标准第10页(共10页)2结合已知条件可得 一x( 9X _361) 9，整理得xy ^Zz .所以 36xy 216z 5 2 5 x 3(a b c)(l a 1) xy z 27 2 20分 二、(本题满分 角形，AB AC , 25分) 如图, DE DC . 点E 在四边形 ABCD 的边AB 上，△ ABC 和厶CDE 都是等腰直角三 ACE 30，求 DP . (1 )由题意知ACB DCE 45 , BC .：2AC , EC 2DC, DCAECAC DC ，所以△ ADC BEC ，故 DAC BC EC45，所以 DAC ACB ，所以 AD // BC .10分 2 )设 AE x , 因为 ACE 30，可得 AC 3x , CE2x , DE 设AC 与DE 交于点P ，如果 (1)证明：AD // BC ；( 2) EBC 解 所以 PE DC 因为 EAP CDP 90 ， EPA CPD ，所以△ APE DPC ，故可得 S APE — 12 S DPC •15分EPC S APES ACE —fx 2 , S EPC S DPC S CDE x 2，于是可得S DPCDPCA2S EPC (3 1)x .(2S 20分 25分PESEPC-个四位数，x 的各位数字之和为 m , x 1的各位数字之和为2的素数.求x .n ，并解 设xabcd , 由题设知 m 与n 若d9,则nm 1 ，所以(m, 若c9 ,则n m 1 9 m 8若b 9, 显然a 9, 所以n m13 , m n 26 39 36 ，矛盾. 若b 9 , 则n m 1 9 9 m于是可得x 8899 或 9799.故(m, n) n 的最大公约数 n) 1，矛盾， 1 9 9 三、(本题满分25分)设x 是 且m 与n 的最大公约数是一个大于(m, n)为大于2的素数.(m,8)，它不可能是大于 2的素数，矛盾，故 c 9 .9 m 26，17，故 ( m, n) ( m,17) 10分故(m, n) ( m, 26) 13，但此时可得17 ,只可能 n 17, m 34 .15分20分 25分。

第十二届“五羊杯”初中数学竞赛试题初二试题(考试时间：90分钟 满分：100分)一、选择题(4选l 型，选对得5分，否则得0分．本大题50分．)1．化简繁分数：=3-2-1--5-4-6--( )(A)32 (B)-32(C)-2 (D)22．化简分式：=+÷++÷++222222)n m n -m ()n m 2mn -(1)n -m n m ()n m 2mn (1-1 (A)2n)(m 4mn + (B) 2n)(m 2mn+ (c)0 (D)23．设a ≠b ，m ≠n ，a ，b ，m ，n 是已知数，则方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++1nb y n a x 1mb y m a x的解是( )．(A)⎪⎪⎩⎪⎪⎨⎧+++=+++=b a n)m)(b (b y b a n)m)(a (a x (B) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)n)(b (a y b -a m)m)(b (a x(C) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)m)(b (b y b -a n)m)(a (a x ((D) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)m)(b (b -y b -a n)m)(a (a x4． 已知x+y ≠0，x ≠z ，y ≠z ，且1+z)-y)(x (x yz ++z)-y)(y (x xz +=z)-z)(y -(x xy，则必有( )．(A)x ＝0 (B)y ＝0 (C)z ＝0 (D)xyz ＝05.一共有( )个整数x 适合不等式|x-2 000|+|x|≤9 999． (A)lO 000 (B)2 000 (C)9 999 (D)8 0006．方程组⎪⎩⎪⎨⎧=+=+=+2xy z 2xz y 2yz x ，的解共有( )组．(A)l (B)2 (C)3 (D)≥47．设，2为自然数，A ＝14444n 2n +⋯+⋯位位，则( )．(A)A 为完全平方数 (B)A 为7的倍数(C)A 恰好有3个约数 (D)以上结论都不对8．设轮船在静水中的速度为v ，该船在流水(速度为u<v)中从上游A 驶往下游B ，再返回A ，所用时间为T ；假设u ＝0，即河流改为静水，该船从A 至B 再返回A ，所用时间为t.则( )．(A)T=t (B)T<t (C)T>t (D)不能确定T ，t 的大小关系 9．如图，长方体ABCD —A'B'C'D ’长、宽、高分别为a ，b ，c ．用它表示一个蛋糕，横切两刀、纵切一切再立切两刀，可分成2×3×3＝18块大小不一的小长方体蛋糕，这18块小蛋糕的表面积之和为( )．(A)6(ab+bc+ca) (B)6(a+c)b+4ca (C)4(ab+bc+ca) (D)无法计算10．打字员小金连续打字14分钟，打了2 098个字符，测得她第一分钟打了112个字符，最后一分钟打了97个字符．如果测算她每一分钟所打字符的个数，则( )不成立， (A)必有连续2分钟打了至少315个字符 (B)必有连续3分钟打了至少473个字符 (C)必有连续4分钟打了至少630个字符 (D)必有连续6分钟打了至少946个字符二、填空题(每小题填对得5分，不填、多填、少填、填错、仅部分填对均得0分．本大题满分50分．)1．分解因式：(x-2)3-(y-2)3-(x-y)3＝ ．2．已知2222)(x C2x B 1-x A 2)1)(x -(x 3x ++++=++，其中A ，B ，C 为常数，则A ＝ ，B ＝ ，C ＝ ，3．化简：xy-y)x -(x -x xyz zx x)y (z x xz -y yz -z)x -(y x yz x 222222++++++++=4．若x-y＝l，x3-y3＝4，则x13-y13＝．5. 已知x6+4x5+2x4-6x3-3x2+2x+l＝[f(x)]2，其中f(x)是x的多项式，则f(x)＝．6．设自然数N是完全平方数，N至少是3位数，它的末2位数字不是00，且去掉此2位数字后，剩下的数还是完全平方数．则N的最大值是．7．设自然数x>y，x+y＝667，x，y的最小公倍数为P，最大公约数为Q，P＝120Q，则x-y 的最大值为 .8．方程4x2-2xy-12x+5y+ll＝0有组正整数解，9．一个油罐有进油龙头P和出油龙头Q．油罐空时，同时打开P、Q，4小时可注满油罐．油罐满时，先打开Q，12小时后关上；接着打开P，2小时后关上，此时油罐未满；再打开Q，5小时后油罐恰好流空．那么P的流量是，Q的流量的倍．10．如图，试把0，3，5，6，7，8，9这7个数填入图中的7个小圈，每个圈填1个数，不同的圈填不同的数．然后在两端填了x和y的每条边上标上|x-y|的数值，使得图中的9条边所标的数值刚好是1，2，3，4，5，6，7，8，9．(答案填在本题图中)初二答案一、1．B．2．A． 3．D．4．D．以(x+y)(x-z)(y-2)乘原式两边，化简得xyz=O．5．C．若x≥2 000，则不等式变为(x一2000)+x≤9 9 9 9，即2000≤x≤5 9 9 9．5，共有4000个整数适合；若O≤x<2000，则不等式变为(2000一x)+x≤9 9 9 9，2 000≤9 9 9 9，恒成立，又有2000个整数适合；若x<O，则不等式变为(2000-x)+(-x)≤9 99 9，即-3 99 9．5≤x< O，共有3 99 9个整数适合．合计有9 9 9 9个整数适合题设不等式． 6．B．有两组解：x=y=z=1，x=y=z=2，7．A．易见A=44···488···89(n个4，n-1个8)，记为An．则A1=49=72，A2=4489．=672，A3=444889=6672，…，An=66…6 72(n-1个6),A是完全平方数．但A2不是7的倍数．A3能被1，2 3，2 9，6 6 7等整除，不止3个约数．8．C．设A，B相距S,T/t>1．T>t．9．B．面积和=2×3×ab+2×2×ac+2×3×bc=6ab+4ac+6bc．1 O．_D．小金中间的l 2分钟打了2 09 8一ll 2—9 7=1889个字符．把这1 2分钟分别平均分成6段、4段、3段，每段2分钟、3分钟、4分钟，由1 88 9÷6：3 1 4…5，1 88 9÷4=4 7 2…1，1 889÷3=6 29…2，应用抽屉原理知(A)，(B)，(C)均成立．但1 8 8 9÷2—944…1，因此如果小金每分钟所打字符个数依次是11 2，15 8，1 5 7，1 58，1 5 7，1 58，157,l 5 8，1 5 7，1 5 8，l 5 7，1 5 7，1 5 7，9 7，则她连续6分钟最多打了3×(1 5 8+1 5 7)=94 5个字符，结论(D)不成立．二、1．3(x一2)(y一2)(z—y)．．2．4/9；5/9； -7/3 通分，分子相等，是恒等式3．0．4．5 2 1．5．±(x3+2x2-x-1)．6．1 6 8 1．设N=x2，x为自然数，N的末2位数字组成整数y，去掉此2位数字后得到整数M，M=m2，m为自然数，则1≤y≤99，x2=1OOm2+y，y=x2—100m2=(x+1Om)(x-1Om)．令x+10m=a，x-1OOm=b，则b≥l，m≥1，x=1Om+b≥11，a=x+10m≥21，我们要求x的最大值．若m≥4，则x=10m+b≥4 1，a=x+10m≥81，唯有b=1，m=4，x=41，a=81，y=81，M=1 6，N=1681．显然当m≤3时，z≤4 O，故N=1 6 81为所求最大值．10．答案如图．(此图旋转或翻折亦符合题意)把标上数值a的边称为“边a’’．则边9两端必为0，9；边8两端必为O，8；边7两端必为0，7．0必与9，8，7相邻．O不能再与其他数相邻．从而边6两端必为9，3；边5两端必为8，3．若O在圆周上，由3与8，9相邻，以及边4的两端必为9，5或7，3，便可填得上图．若O在中央，易见不能有符合要求的图形．第十三届“五羊杯”初中数学竞赛试题初二试题(考试时间：90分钟 满分：100分)一、选择题(本大题共10小题，每小题5分，共50分，)1．化简繁分数：=8-7-6-7--3-2-8-9--5-4-6-7--2-1-8-9--( )(A)-35 (B) 35 (C)-53(D)以上答案都不对2．设a ：b=3：5，求下式的值：333322222222b)-(a b)(a b)-(a -b)(a b a b -4a -b a 4b -a b -a b6a -b -a 6b a +++÷++++＝( )． (A)-92616175 (B) 30671235 (C)9157 (D) 73 3．已知x-2x 1＝2，则以下结论中，；①54x 1x 22=+②118x 1-x 33=③5432x 1x 55=+ 有( )个是正确的：(A)3 (B)2 (C)l (D)04.方程组 ⎪⎪⎩⎪⎪⎨⎧==+2by-cx axy 1cy bx axy(b ≠2c ，c ≠-2b)的解是( )，(A) ⎪⎪⎩⎪⎪⎨⎧++=++=c)a(2b )c 2(b y c)a(2b )c 2(b x 2222 (B) ⎪⎪⎩⎪⎪⎨⎧+=+=b)-a(2c )c 2(b y b)-a(2c )c 2(b x 2222(C) ⎪⎪⎩⎪⎪⎨⎧++=+=)a(2b )c 2(b y b)-a(2c )c 2(b x 2222c (D) ⎪⎪⎩⎪⎪⎨⎧+=++=b)-a(2c )c 2(b y c)a(2b )c 2(b x 22225.下面的图形中，共有( )个可以一笔画(不重复也不遗漏，下笔后笔不能离开纸)．(A)0 (B)l (C)2 (D)36.三位数中，十位数字比百位和个位数字都要大的三位数有 ( )个． (A)315 (B)240 (C)200 (D)1987．5支足球队进行循环比赛(每两支球队都赛一场)，已知甲队已赛3场，乙队比甲队赛的场数多，丙队比甲队赛的场数少，丁队与戊队赛的场数一样多，但丁队与戊队没赛过．那么，总的比赛场数是( )． (A)8 (B)7 (C)6 (D)58．如图，梯形ABCD 被对角线分为四个小三角形．已知△AOB 和△BOC 的面积分别为25m 2和35m 2，那么梯形的面积是( ) m 2． (A)144 (B)140 (C)160 (D)无法确定9．一个平面图形，如果沿着一条直线对折能做到自身重合，便称为轴对称图形，例如正方形是轴对称图形(因为沿它的一条对角线对折，可做到自身重合)．在下图中的4个图形中有( )个是轴对称图形．(A)4 (B)3 (C)2 (D)l10．下面算式中，每个汉字代表0，l ，2，……，9中的一个数字，不同的汉字代表不同的数字．算式中的乘数应是( )．(A)2 (B)3 (C)4 (D)≥5二、填空题(本大题共10小题，每小题5分，共50分，)1．分解因式：(2x-3y)3+(3x-2y)3－125(x-y)3＝ ．2.已知2x CBx 1x A 2)1)(x (x 12x 3x 222++++=++++，其中A ，B ，C 为常数，则B ＝ ． 3.化简：b)-a)(c -(c b)(a 2c a)-c)(b -(b a)(c 2b c)-b)(a -(a c)b)(a a(a 22++++++= . 4．若(x-1)(y+1)＝3，xy(x-y)＝4，则x 7-y 7＝ ．5．已知6x 2+7xy-3y 2-8x+10y+c 是两个x ，y 的一次多项式的乘积，而c 是常数，则c ＝ 6．设n 是三位完全平方数，且n 的逆排数(把的数字从右到左逆排所得的数)也是完全平方数，这样的数n 共有 个．7．已知a 、b 和9的最大公约数为1，最小公倍数为72，则a+b 的最大值是 8．方程y143x ＝3有 组正整数解． 9．一个深水井，现有5 000立方米储水量，并且地下水以每秒0．5立方米的流量涌进井内，但水井储水量达到7000立方米时便停止涌水．水井安装有往外抽水的水泵4台，每台每秒出水量0．2立方米，如果开始每天白天(7～19时)开3台水泵，晚上(19—7时)开l 台水泵，3天后，改为白天开4台水泵，要使每台水泵的出水量不减少，最多能开小时?(答案四舍五入为整数)10．花城中学初22(A)班的女同学计划制作200张贺年卡．如果每人做8张，任务尚未完成；如果每人做9张，则超额完成任务．后来决定增派4位男同学参加制作，任务改为300张，结果每人做了11张，超额完成了任务，那么，初二(A)班女同学共有 人．初 二答案一、1．A ．2.C3．B ．4．C ．5．D ．6．B ．7．C ．乙队已赛过4场．若丙队只赛过1场，则丙队与甲队没赛过。

第十二届“五羊杯”初中数学竞赛试题初二试题(考试时间：90分钟 满分：100分)一、选择题(4选l 型，选对得5分，否则得0分．本大题50分．)1．化简繁分数：=3-2-1--5-4-6--( ) (A)32 (B)-32 (C)-2 (D)2 2．化简分式：=+÷++÷++222222)n m n -m ()n m 2mn -(1)n -m n m ()n m 2mn (1-1 (A)2n)(m 4mn + (B) 2n)(m 2mn + (c)0 (D)2 3．设a ≠b ，m ≠n ，a ，b ，m ，n 是已知数，则方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++1nb y n a x 1m b y m a x 的解是( )． (A)⎪⎪⎩⎪⎪⎨⎧+++=+++=b a n)m)(b (b y b a n)m)(a (a x (B) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)n)(b (a y b -a m)m)(b (a x (C) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)m)(b (b y b -a n)m)(a (a x ((D) ⎪⎪⎩⎪⎪⎨⎧++=++=b -a n)m)(b (b -y b -a n)m)(a (a x 4． 已知x+y ≠0，x ≠z ，y ≠z ，且1+z)-y)(x (x yz ++z)-y)(y (x x z +=z)-z)(y -(x x y ，则必有( )．(A)x ＝0 (B)y ＝0 (C)z ＝0 (D)xyz ＝05.一共有( )个整数x 适合不等式|x-2 000|+|x|≤9 999．(A)lO 000 (B)2 000 (C)9 999 (D)8 0006．方程组⎪⎩⎪⎨⎧=+=+=+2xy z 2xz y 2yz x ，的解共有( )组．(A)l (B)2 (C)3 (D)≥47．设，2为自然数，A ＝14444n 2n +⋯+⋯位位，则( )．(A)A 为完全平方数 (B)A 为7的倍数(C)A 恰好有3个约数 (D)以上结论都不对8．设轮船在静水中的速度为v ，该船在流水(速度为u<v)中从上游A 驶往下游B ，再返回A ，所用时间为T ；假设u ＝0，即河流改为静水，该船从A 至B 再返回A ，所用时间为t.则( )．(A)T=t (B)T<t (C)T>t (D)不能确定T ，t 的大小关系9．如图，长方体ABCD —A'B'C'D ’长、宽、高分别为a ，b ，c ．用它表示一个蛋糕，横切两刀、纵切一切再立切两刀，可分成2×3×3＝18块大小不一的小长方体蛋糕，这18块小蛋糕的表面积之和为( )．(A)6(ab+bc+ca) (B)6(a+c)b+4ca(C)4(ab+bc+ca) (D)无法计算10．打字员小金连续打字14分钟，打了2 098个字符，测得她第一分钟打了112个字符，最后一分钟打了97个字符．如果测算她每一分钟所打字符的个数，则( )不成立，(A)必有连续2分钟打了至少315个字符(B)必有连续3分钟打了至少473个字符(C)必有连续4分钟打了至少630个字符(D)必有连续6分钟打了至少946个字符二、填空题(每小题填对得5分，不填、多填、少填、填错、仅部分填对均得0分．本大题满分50分．)1．分解因式：(x-2)3-(y-2)3-(x-y)3＝ ． 2．已知2222)(x C 2x B 1-x A 2)1)(x -(x 3x ++++=++，其中A ，B ，C 为常数，则A ＝ ，B ＝ ，C ＝ ，3．化简：xy -y)x -(x -x xy z zx x)y (z x xz -y yz -z)x -(y x yz x 222222++++++++= 4． 若x-y ＝l ，x 3-y 3＝4，则x 13-y 13＝ ．5. 已知x 6+4x 5+2x 4-6x 3-3x 2+2x+l ＝[f(x)]2，其中f(x)是x 的多项式，则f(x)＝ ．6．设自然数N 是完全平方数，N 至少是3位数，它的末2位数字不是00，且去掉此2位数字后，剩下的数还是完全平方数．则N 的最大值是 ．7．设自然数x>y ，x+y ＝667，x ，y 的最小公倍数为P ，最大公约数为Q ，P ＝120Q ，则x-y 的最大值为 .8．方程4x 2-2xy-12x+5y+ll ＝0有 组正整数解，9．一个油罐有进油龙头P 和出油龙头Q ．油罐空时，同时打开P 、Q ，4小时可注满油罐．油罐满时，先打开Q ，12小时后关上；接着打开P ，2小时后关上，此时油罐未满；再打开Q ，5小时后油罐恰好流空．那么P 的流量是，Q 的流量的 倍．10．如图，试把0，3，5，6，7，8，9这7个数填入图中的7个小圈，每个圈填1个数，不同的圈填不同的数．然后在两端填了x 和y 的每条边上标上|x-y|的数值，使得图中的9条边所标的数值刚好是1，2，3，4，5，6，7，8，9．(答案填在本题图中)初二答案一、1．B．2．A． 3．D．4．D．以(x+y)(x-z)(y-2)乘原式两边，化简得xyz=O．5．C．若x≥2 000，则不等式变为(x一2000)+x≤9 9 9 9，即2000≤x≤5 9 9 9．5，共有4000个整数适合；若O≤x<2000，则不等式变为(2000一x)+x≤9 9 9 9，2 000≤9 9 9 9，恒成立，又有2000个整数适合；若x<O，则不等式变为(2000-x)+(-x)≤9 99 9，即-3 99 9．5≤x< O，共有3 99 9个整数适合．合计有9 9 9 9个整数适合题设不等式． 6．B．有两组解：x=y=z=1，x=y=z=2，7．A．易见A=44···488···89(n个4，n-1个8)，记为An．则A1=49=72，A2=4489．=672，A3=444889=6672，…，An=66…6 72(n-1个6),A是完全平方数．但A2不是7的倍数．A3能被1，2 3，2 9，6 6 7等整除，不止3个约数．8．C．设A，B相距S,T/t>1．T>t．9．B．面积和=2×3×ab+2×2×ac+2×3×bc=6ab+4ac+6bc．1 O．_D．小金中间的l 2分钟打了2 09 8一ll 2—9 7=1889个字符．把这1 2分钟分别平均分成6段、4段、3段，每段2分钟、3分钟、4分钟，由1 88 9÷6：3 1 4…5，1 88 9÷4=4 7 2…1，1 889÷3=6 29…2，应用抽屉原理知(A)，(B)，(C)均成立．但1 8 8 9÷2—944…1，因此如果小金每分钟所打字符个数依次是11 2，15 8，1 5 7，1 58，1 5 7，1 58，157,l 5 8，1 5 7，1 5 8，l 5 7，1 5 7，1 5 7，9 7，则她连续6分钟最多打了3×(1 5 8+1 5 7)=94 5个字符，结论(D)不成立．二、1．3(x一2)(y一2)(z—y)．．2．4/9；5/9； -7/3 通分，分子相等，是恒等式3．0．4．5 2 1．5．±(x3+2x2-x-1)．6．1 6 8 1．设N=x2，x为自然数，N的末2位数字组成整数y，去掉此2位数字后得到整数M，M=m2，m为自然数，则1≤y≤99，x2=1OOm2+y，y=x2—100m2=(x+1Om)(x-1Om)．令x+10m=a，x-1OOm=b，则b≥l，m≥1，x=1Om+b≥11，a=x+10m≥21，我们要求x的最大值．若m≥4，则x=10m+b≥4 1，a=x+10m≥81，唯有b=1，m=4，x=41，a=81，y=81，M=1 6，N=1681．显然当m≤3时，z≤4 O，故N=1 6 81为所求最大值．10．答案如图．(此图旋转或翻折亦符合题意)把标上数值a的边称为“边a’’．则边9两端必为0，9；边8两端必为O，8；边7两端必为0，7．0必与9，8，7相邻．O不能再与其他数相邻．从而边6两端必为9，3；边5两端必为8，3．若O在圆周上，由3与8，9相邻，以及边4的两端必为9，5或7，3，便可填得上图．若O在中央，易见不能有符合要求的图形．第十三届“五羊杯”初中数学竞赛试题初二试题(考试时间：90分钟 满分：100分)一、选择题(本大题共10小题，每小题5分，共50分，)1．化简繁分数：=8-7-6-7--3-2-8-9--5-4-6-7--2-1-8-9--( ) (A)-35 (B) 35 (C)-53 (D)以上答案都不对 2．设a ：b=3：5，求下式的值：333322222222b)-(a b)(a b)-(a -b)(a b a b -4a -b a 4b -a b -a b 6a -b -a 6b a +++÷++++＝( )． (A)-92616175 (B) 30671235 (C)9157 (D) 73 3．已知x-2x 1＝2，则以下结论中，；①54x 1x 22=+②118x 1-x 33=③5432x1x 55=+ 有( )个是正确的：(A)3 (B)2 (C)l (D)04.方程组 ⎪⎪⎩⎪⎪⎨⎧==+2by-cx axy 1cy bx axy (b ≠2c ，c ≠-2b)的解是( )， (A) ⎪⎪⎩⎪⎪⎨⎧++=++=c)a(2b )c 2(b y c)a(2b )c 2(b x 2222 (B) ⎪⎪⎩⎪⎪⎨⎧+=+=b)-a(2c )c 2(b y b)-a(2c )c 2(b x 2222 (C) ⎪⎪⎩⎪⎪⎨⎧++=+=)a(2b )c 2(b y b)-a(2c )c 2(b x 2222c (D) ⎪⎪⎩⎪⎪⎨⎧+=++=b)-a(2c )c 2(b y c)a(2b )c 2(b x 22225.下面的图形中，共有( )个可以一笔画(不重复也不遗漏，下笔后笔不能离开纸)．(A)0 (B)l (C)2 (D)36.三位数中，十位数字比百位和个位数字都要大的三位数有 ( )个．(A)315 (B)240 (C)200 (D)1987．5支足球队进行循环比赛(每两支球队都赛一场)，已知甲队已赛3场，乙队比甲队赛的场数多，丙队比甲队赛的场数少，丁队与戊队赛的场数一样多，但丁队与戊队没赛过．那么，总的比赛场数是( )．(A)8 (B)7 (C)6 (D)58．如图，梯形ABCD 被对角线分为四个小三角形．已知△AOB 和△BOC 的面积分别为25m 2和35m 2，那么梯形的面积是( ) m 2．(A)144 (B)140 (C)160 (D)无法确定9．一个平面图形，如果沿着一条直线对折能做到自身重合，便称为轴对称图形，例如正方形是轴对称图形(因为沿它的一条对角线对折，可做到自身重合)．在下图中的4个图形中有( )个是轴对称图形．(A)4 (B)3 (C)2 (D)l10．下面算式中，每个汉字代表0，l ，2，……，9中的一个数字，不同的汉字代表不同的数字．算式中的乘数应是( )． (A)2 (B)3 (C)4 (D)≥5二、填空题(本大题共10小题，每小题5分，共50分，)1．分解因式：(2x-3y)3+(3x-2y)3－125(x-y)3＝ ．2.已知2x C Bx 1x A 2)1)(x (x 12x 3x 222++++=++++，其中A ，B ，C 为常数，则B ＝ ．客上天然居 × 好居然天上客3.化简：b)-a)(c -(c b)(a 2c a)-c)(b -(b a)(c 2b c)-b)(a -(a c)b)(a a(a 22++++++= . 4．若(x-1)(y+1)＝3，xy(x-y)＝4，则x 7-y 7＝ ．5．已知6x 2+7xy-3y 2-8x+10y+c 是两个x ，y 的一次多项式的乘积，而c 是常数，则c ＝6．设n 是三位完全平方数，且n 的逆排数(把的数字从右到左逆排所得的数)也是完全平方数，这样的数n 共有 个．7．已知a 、b 和9的最大公约数为1，最小公倍数为72，则a+b 的最大值是8．方程y143x +＝3有 组正整数解． 9．一个深水井，现有5 000立方米储水量，并且地下水以每秒0．5立方米的流量涌进井内，但水井储水量达到7000立方米时便停止涌水．水井安装有往外抽水的水泵4台，每台每秒出水量0．2立方米，如果开始每天白天(7～19时)开3台水泵，晚上(19—7时)开l 台水泵，3天后，改为白天开4台水泵，要使每台水泵的出水量不减少，最多能开小时?(答案四舍五入为整数)10．花城中学初22(A)班的女同学计划制作200张贺年卡．如果每人做8张，任务尚未完成；如果每人做9张，则超额完成任务．后来决定增派4位男同学参加制作，任务改为300张，结果每人做了11张，超额完成了任务，那么，初二(A)班女同学共有 人．初 二答案一、1．A ．2.C3．B ．4．C ．5．D ．6．B ．7．C ．乙队已赛过4场．若丙队只赛过1场，则丙队与甲队没赛过。

第18届“五羊杯”初一数学竞赛试题（考试时间：90分钟 满分：100分）一、选择题（每小题5分，共50分）1、已知有理数,,,a b c d 满足20069153268a b c d ====，那么（ ） A 、a b c d >>> B 、a b c d <<<C 、9153268a b c d +>+>+>+D 、9153268a b c d +=+=+=+ 2、计算：2.6×0.000093－(0.0003×3.1－9300×0.000000074)=( ) A 、0.0013764 B 、0.0004836 C 、0.00186 D 、03、计算：564 2.5322981 4.54⨯÷+⨯÷=⨯÷+⨯÷( )A 、52B 、103C 、209D 、4094、已知有理数,,,A B x y 满足0A B +≠，且():()(2):()A B A B x y x y +-=+-，那么:()A A B +=（ ）A ．3:(2)x x y +B ．3:(42)x x y +C ．:()x x y +D ．2:(2)x x y + 5．2006和3007的最大公约数是（ ）． A ．1 B ．7 C ．11 D ．13 6．531172006200620065315⨯+⨯+⨯ 的计算结果是一个（ ）．A ．无限循环小数B ．有限小数C ．无限不循环小数D ．整数7、把17写成a b c ++的形式，其中,,a b c 是整数，0a b c <<<，共有（ ）种写法．A ．15B ．16C ．17D ．188．设整数n 满足0<n<1000，n=11×,a a 也是整数，而且n 的各位数字和恰好也是a ，那么这样的n （ ）．A ．至少有3个B ．恰有2个C ．刚好有1个D ．不存在 9．关于x 的一元一次方程20062008201020122005200720092011x x x---+=+的解（ ）．A 、是一个大于1000的数B 、是一个两位的自然数C 、是一个大于0且小于2的数D 、不存在10、设A、B、C、D为大于的整数，满足算式14.451212ABCD=+++，那么A+B+C+D=（）A、9B、10C、11D、12二、填空题（每小题答对得5分，否则得0分，本大题满分50分）11、A是整数，A＞0，且2006－A是一个完全立方数，则A的最小值是12、如果五羊牌越野汽车的车牌号码为“AB12”这种类型，即开头两个是英文字母（可以相同），后面两个是阿拉伯数字（可以相同），那么，这样的车牌号码一共有个13、如果3456789200634567892008,4567892006345678920064A B==，C=1，D=0，那么A、B、C、D的大小顺序（从小到大）是14、如果A、B、C是三个质数，而且A－B=B－C=14，那么这样的A、B、C组成的数组（A，B，C）共有组15、如图是2008年6月的日历，杨小武该月每周都要参加一次足球训练，日程安排是：星期日、星期一和星期六安排去一次，星期三去两次。

八年级数学竞赛试卷考试时间：100分钟 总分：150分姓名： 班级： 得分：一、选择题（每题5分，共50分）1、下列各式成立的是（ ）A ．a-b+c=a-（b+c ）B ．a+b-c=a-（b-c ）C ．a-b-c=a-（b+c ）D ．a-b+c-d=（a+c ）-（b-d ）2、已知一次函数y=kx+b 的图象（如图6），当y ＜0时，x 的取值范围是（（A ）x ＞0（B ）x ＜0 （C ）x ＜1 （D ）x ＞1 3、在△ABC 中，∠B ＝∠C ，与△ABC 全等的三角形有一个角是100100°角对应相等的角是 （ ）A.∠AB.∠BC.∠CD.∠B 或∠C4、某校八（2）班的全体同学喜欢的球类运动用图7所示的扇形统计图来表示，下面说法正确的是（ ）A 、从图中可以直接看出喜欢各种球类的具体人数；B 、从图中可以直接看出全班的总人数；C 、从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况；D 、从图中可以直接看出全班同学现在喜欢各种球类的人数的大小关系5、已知一次函数y=mx+│m+1│的图像与y 轴交于点（0，3），且y 随x 的增大而减小，则m 的值为（ ）．A ．2B ．-4C ．-2或-4D ．2或-46、设y=ax 15+bx 13+cx 11-5(a 、b 、c 为常数)，已知当x=7时，y=7，则x= -7时，y 的值等于( )A 、-7B 、-17C 、17D 、不确定7、已知b>a>0，a 2+b 2=4ab ，则ba b a -+等于( )． A ．-21B ． 3C ．2D ．-38、将一个正方形分割成n 个小正方形(n>1)，则n 不可能取( )．A ．4B ．5C ．8D ．99、若x 取整数，则使分式1-2x 36x +的值为整数的x 值有( )． (A)3个 (B)4个 (C)6个 (D)8个10、已知1x ，2x ，3x 的平均数为5,1y ,2y ,3y 的平均数为7，则1123x y +，2223x y +，3323x y +的平均数为( )(A)31 (B)313 (C)935 (D)17二、填空题（每题8分，共40分）11、点O 为线段 A B 上一点， ∠AOC = 10︒ ， ∠COD = 50︒ ，则 ∠BOD = 或A O B12、已知 m ＞0 ，且对任意整数 k ，2018123k m+均为整数，则 m 的最大值为 ． 13、已知某三角形的三条高线长 a ，b ，c 为互不相等的整数，则 a + b + c 的最小值 为 ．14、如果用四则运算的加、减、除法定义一种新的运算，对于任意实数x 、y 有则=15、如图5所示，圆的周长为4个单位长度，在圆的4等分点处标上0，1，2，3．先让圆周上数字0所对应的数与数轴上的数－1所对应的点重合，再让数轴按逆时针方向绕在该圆上，那么数轴上的数－2007将与圆周上的数字_________重合．二、简答题（每题20分，共60分） 16、现有两种理财方式供王老师选择．方案一：购买一款分红产品，前三年每年 年初交 10 万元，第 6 年年初返 6 万元，以后每年处返1.5 万元；方案二：购 买一款年利率 5%，满一年计息的储蓄产品，第一年初存款10 万元，接下来 两年每年年初追加本金 10 万元，并将之前的本息全部续存．请问哪个选择更划算？请说明理由．（参考数据：1.054 + 1.053 + 1.052 =3.47563125 ）y x yx y x -+=*()()31*191211**017、一筐苹果，若分给全班同学每人3个，则还剩下25 个；若全班同学一起吃，其中5个同学每人每天吃1个，其他同学每人每天吃2个，则恰好用若干天吃完．问筐里最多共有多少个苹果？18、如图所示，有一张长为3、宽为1的长方形纸片，现要在这张纸片上画两个小长方形，使小长方形的每条边都与大长方形的一边平行，并且每个小长方形的长与宽之比也都为3:1，然后把它们剪下，这时，所剪得的两张小长方形纸片的周长之和有最大值．求这个最大值．八年级答案：一、C CADB BDBBA二、11、120度或者140度12、2/3 13、9 14、163/113 15、2 三、1617、18、。