当前位置：文档之家 › 第六章弯曲应力

第六章弯曲应力

  • 格式：doc
  • 大小：1.28 MB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

工程力学B(二)第11讲第六章弯曲应力-强度条件

工程力学B(二)第11讲第六章弯曲应力-强度条件

τ σ
4 减小应力集中。尽量避免截面尺寸沿梁的急剧变化。尽量 减小应力集中。尽量避免截面尺寸沿梁的急剧变化。 使用圆角过渡。 使用圆角过渡。
局部考虑
1.截面的放置 截面的放置 与 2.同样面积下 最大 同样面积下W最大 同样面积下
〉
〉
〉
为什么？ 为什么？
〉
〉
常见梁截面的 Wz /A 值 Wz /A 的值 大与小，哪个好？为什么？ 大与小，哪个好？为什么？
W ( x) =
M ( x)
[σ ]
二、变截面梁与等强度梁
横截面沿梁轴变化的梁，称为变截面梁。 横截面沿梁轴变化的梁，称为变截面梁。
F
x
F
b
h(x )
z
y
l
h1
hmax
σ max =
M ( x) = [σ ] W ( x)
W ( x) =
M ( x)
[σ ]
bh 2 6 Fx M ( x ) = Fx, h = 常数，由 Wz = 知h ( x ) = 6 b[σ ]
由τ max =
hmax =
6 Fl b[σ ]
3 Fs 3F 知h1 = 2 bh 2b[τ ]
三、梁的合理受力 梁的合理受力
1.支座位置 合理布置支座位置，使 M max 尽可能小 支座位置 合理布置支座位置，
q L
qL2 40
M
2 qL 8
x
q L/5 L/5
M
2 −qL 50
x
2.加载方式 加载方式——合理布置外力作用，使 M max 尽可能小 合理布置外力作用， 加载方式 合理布置外力作用
Fl 当载荷位于梁跨度中间时， 当载荷位于梁跨度中间时，弯矩最大 Wz ≥ = 3.0 × 10 − 4 m 3 4[σ ]

第六章__弯曲应力及剪力流的知识点

第六章__弯曲应力及剪力流的知识点
Page 4
第六章 弯曲应力
上一讲回顾（12）
•梁变形与受力假设：平面假设，单向受力假设。 y My s •正应力公式： s E E Iz M Iz s max •最大正应力： Wz Wz y S z ydA, S y zdA •静矩：
A A
•惯性矩与惯性积 ：

50
a
F l
a
a = ? [ F ] 最大.
Page
27
第六章 弯曲应力
配重降低最大弯矩作用分析
M
Pa Pa F P
F a
P
l
a
a
l
a
M
Fl/4 +
M
Fl/4-Pa Pa
+
Pa
Page 28
第六章 弯曲应力
弯拉（压）组合分析
A F
l 2
q
B
C
l 2
F
C
FN M max
sN

sM
y
sN sM

20 kN 20 kN
C
D
解：计算截面形心 与惯性矩
A
B
1m
3m
1m
yC 139mm I z 40.3 106 mm 4
M 图:

10kN m

20kN m
200
为校核梁的强度，需计算 B截面a点的拉应力与b点 压应力，C截面b点拉应力
a
30
y1
z
170
yC
b 30
Page 19
3. 弯矩计算 或
EI z
bd 2s max M s max W 1.14kNM 6

第6章 弯曲应力

第6章 弯曲应力

称为抗弯截面系数
只有一根对称轴的横截面形状: yt，max yc，max O y
O y
z
t,max
My t ,max Iz
c,max
Myc,max Iz
z
简单截面的弯曲截面系数 b h ⑴ 矩形截面
z
bh3 Iz 12 b3h Iy 12
⑵ 圆形截面
y d
Iz bh2 Wz h/2 6 Iy b2h Wy 源自/2 63()
Ⅱ .纯弯曲理论的推广 对于细长梁（ l/h > 5 ），纯弯曲时的正应力计算 公式用于横力弯曲情况，其结果仍足够精确。 F
l
M ( x) y Iz
Fl
4
max
M ( x) Wz
解：
由弯曲曲率公式 可得：
M EIz
M EI z
1
代入弯曲正应力公式：
M EIZ Ed 533.3MPa WZ WZ 2
3.正应力的正负号与弯矩 及点的坐标 y的正负号有关。实际计算中，可根 据截面上弯矩的方向，直接判断中性 轴的哪一侧产生拉应力，哪一侧产生 压应力，而不必计及M和y的正负。
三、最大弯曲正应力 有两根对称轴的横截面形状: b h
z
y y
z
max
M M Mymax I z Wz Iz y max

基本假设2:
梁内各纵向纤维无挤压 假设，纵向纤维间无正应 力。

中性层与中性轴
纵向对称面 中性层 Z 中性轴
中性层 根据变形的连续性 可知，梁弯曲时从其凹 入一侧的纵向线缩短区 到其凸出一侧的纵向线 伸长区，中间必有一层 纵向无长度改变的过渡 层，称为中性层 。 中性轴: 中性层与横截面的交 线就是中性轴。

第6章 弯曲应力

第6章 弯曲应力

∗ FQ Sz
(
)
6.3 弯曲切应力
工字形截面梁
FQ B 2 2 b h2 2 τ= H − h + − y Iz b 8 2 4
(
)
h 分别代入： 以y = 0和y = ± 分别代入： 2
τ max
FQ BH 2 b Bh 2 = − (1 − ) Iz b 8 B 8
τmin =
∗ FQmax Sz
dI z
40×103 ×85140.97 = = 31.6MPa 7 6.5×1.66×10
3 工字钢梁最大弯曲剪应力的近似计算。 工字钢梁最大弯曲剪应力的近似计算。 腹板上平均剪应力为： 腹板上平均剪应力为：
40×103 τ= = = 38.8MPa A (180 − 2×10.7)×6.5 1 FQ
τmax =
∗ F max Sz max Q
dIz
=
∗ d ⋅ I z / Sz max
F max Q
40×103 = = 40.0MPa 6.5×15.4×10
2 求腹板上最小剪应力 最小剪应力位于腹板与翼缘交界处。 最小剪应力位于腹板与翼缘交界处。
6.3 弯曲切应力
∗ Sz = (10.7×94)×(180 / 2 −10.7 / 2) = 85140.97mm3
A
6.2 弯曲正应力
纯梁弯曲
因 FQ =0 所以 τ = 0，σ ≠ 0 ，
纵线 横线
m b a m M a m
n b a n
一、变形特点 纵线： 纵线： 变为同心圆弧线； 变为同心圆弧线； 凹侧缩短，凸侧伸长。 凹侧缩短，凸侧伸长。 横线： 横线： 仍为直线，且垂直于纵线； 仍为直线，且垂直于纵线； 不同横截面相对转过一个角度。 不同横截面相对转过一个角度。

工程力学教学 第6章 弯曲应力

工程力学教学 第6章 弯曲应力

17
max
M Iz
ymax
令
Wz
Iz , ymax
上式可改写为
max
M Wz
Wz 称为抗弯截面模量，单位：m3。
上述分析是在平面假设下建立的，对于横力弯曲，由于
横截面上还有剪力，变形后截面会发生翘曲，平面假设不再
成立。当截面尺寸与梁的跨度相比很小时，翘曲很小，可按
平面假设分析吗?
整理课件
18
横力弯曲
整理课件
19
6-2
横力弯曲正应力公式
弯曲正应力
M (x) y
IZ
弹性力学精确分析表明， 当跨度 l 与横截面高度 h 之 比 l / h > 5 （细长梁）时， 纯弯曲正应力公式对于横力 弯曲近似成立。
横力弯曲最大正应力
max
Mmaxymax IZ
整理课件
M max
max
Wz
20
弯曲正应力公式适用范围 •纯弯曲或细长梁的横力弯曲
4 2
2 F
3 F
A
s max
A
s max
A
矩形截面 圆形截面 环形截面
根据强度条件可进行下述工程计算：
⑴强度校核；
⑵设计截面尺寸；
⑶确定容许荷载。
整理课件
38
利用强度条件进行工程计算时，需首先确定梁的危险截面。
⑴梁的最大正应力发生在弯矩最大、截面离中性轴最远
点处；变截面梁要综合考虑 M与IZ;脆性材料抗拉和抗压性能
一、矩形截面切应力
基本假设： ⑴截面上各点切应力与剪力同向；
12
M
M+dM
⑵距中性轴等距离各点的切应力相 等。
Fs m n Fs

材料力学第6章-弯曲应力

材料力学第6章-弯曲应力
Chapter Six
Stresses in Bending
第六章 弯曲应力
1
背景材料
本章基本要求 6.1 弯曲正应力 6.2 弯曲切应力 6.3 梁的强度及破坏
6.4 组合变形的应力 本章内容小结
2
背 景
材
料
F
横梁横截面上的应力如 何计算？行车移动时，这种 应力如何变化？
3
汽车在轮轴上的支 承为什么设计为叠板弹 簧的形式？这种结构有 什么优点？
3M max b 44.7 mm 2[ ] 故取 b = 45 mm
27
例6.2 欲把直径为 d 的圆木锯成承受竖直方向荷载的矩 形截面梁，若要使梁具有最大的强度，矩形的高 h 和宽 b
应成什么比例？
d b h
分析
强度最大
荷载相同时应力水平最低
max
M max W
W 为最大
建立 W 函数关系并求其极值
A
A
dA

z dx
A
1) 第一式：
FN dA
A

A
E

y dA
E

A
y dA
E

Sz 0
x
S z 0 重要结论：中性轴必定过形心
2) 第二式：
E
E

y
E M y z dA y zdA I yz A A
mn ( y ) d
z
dx dx x
mn mn ( y )d d mn d


y

m
d
y
n'
n
m'

材料力学第6章弯曲应力


图6.5
页 退出
材料力学
出版社 理工分社
例6.1如图6.6所示，矩形截面悬臂梁受集中力和集中力偶作用。试求Ⅰ—Ⅰ 截面和固定端Ⅱ—Ⅱ截面上A，B，C，D ４点处的正应力。
图6.6
页 退出
材料力学
出版社 理工分社
解矩形截面对中性轴的惯性矩为 对于Ⅰ—Ⅰ截面，弯矩MⅠ=20 kN·m，根据式(6.2)，各点正应力分别为
页 退出
材料力学
出版社 理工分社
(1)变形几何关系 弯曲变形前和变形后的梁段分别表示于图6.4(a)和(b)。以梁横截面的对称 轴为y轴且向下为正(见图6.4(c))。以中性轴为z轴，但中性轴的位置尚待确 定。在中性轴尚未确定之前，x轴只能暂时认为是通过原点的横截面的法 线。根据弯曲平面假设，变形前相距为dx的两个横截面，变形后各自绕中性 轴相对旋转了一个角度dθ ，且仍然保持为平面。这就使得距中性层为y的纵 向纤维bb的长度变为
式中积分
是横截面对y轴和z轴的惯性积。由于y轴是横截面的对
称轴，必然有Iyz=0(见附录)。所以式(g)是自然满足的。 将式(b)代入式(e)，得
式中积分∫Ay2dA=Iz是横截面对z轴(中性轴)的惯性矩。于是式(h)改写为 式中 ——梁轴线变形后的曲率。
页 退出
材料力学
出版社 理工分社
式(6.1)表明，EIz越大，则曲率 越小，故EIz称为梁的抗弯刚度。从式 (6.1)和式(b)中消去 ，得
而对于变截面梁，虽然是等截面梁但中性轴不是横截面对称轴的梁，在计算 最大弯曲正应力时不能只注意弯矩数值最大的截面，应综合考虑My/Iz的值 (参看例6.5和例6.8)。
页 退出
材料力学
出版社 理工分社
引用记号

理论力学 第六章 弯曲应力


Fs 2 q( x2 a L)
qL
图（a） B M2 x2 Fs2
mB (Fi ) 0 , 1 qLx2 M 2 q( x2 a)2 0 2
M2
1 q( x2 a)2 qLx2 2
图（c）
从上面例题的计算过程，可以总结出如下 规律： (1) 横截面上的剪力在数值上等于截面 左侧或右侧梁段上外力的代数和。 左侧梁段上向上的外力或右侧梁段上 向下的外力将引起正值的剪力；反之，则
x
Fab l
Fa l
x
M
a
F
C
l
b * 在 集中力F 作用 处，剪力图有突变， 突变值为集中力的 大小；弯矩图有尖 角转折
A
x Fb l
FS
Fa l
x
Fab l
x
M
a b l / 2时，M max
Fl 为极大值。 4
讨论 由剪力图可见，在梁上 的集中力(包括集中荷载和约
束力)作用处剪力图有突变，
y
F
2.求截面1－1上的内力
FS D
2 FA F 3
2 M D FA a Fa 3
同理,对于C左截面： 2 FSC左 FA F 3 2 l 2 M C左＝ F Fl 3 3 9 对于C右截面：
F l 2 FSC右 FA F M C右 FA Fl 3 3 9 FSC左 FSC右 , M C左＝M C右
M2
FS2
FB
建议：求截面FS和M时，均按规定正向假设，这 样求出的剪力为正号即表明该截面上的剪力为正 的剪力，如为负号则表明为负的剪力。对于弯矩 正负号也作同样判断。
•
§6-3 剪力方程和弯矩方程 剪力图和弯矩图

课件：第六章 弯曲应力


A y0dA 0
同理:
Iz Iz0 a2 A I y I y0 b2 A
Page
Cy0z0－形心直角坐标系 Oyz－任意直角坐标系
二者平行
16
思考：下列计算是否正确？ 其中C是截面形心。
IZ2 IZ1 Aa2
•C
解：不正确。
z1
a
因为 Z1 不是形心轴
z2
Page
17
典型截面的惯性矩与抗弯截面系数 ( d D)
( y) 1 dF
b dx
l F dA
My
Iz
M Iz
y * dA
ydA Sz ( )
MSz ( )
Iz
Sz()－面积 对中性轴 z 的静矩
l
( y) Sz ( ) dM
bIz dx
( y) FSSz ( )
I zb Page
1
2
M
M dM
y
FS
FS
y* mn
1
2
x
dx
d
l 2 0
0.002
3
x l
4(
x l
)2
dx
l l 2
0.002 1
x l
dx
0.002
3l 2
( x )2 l
l
4l 3
(
x l
)3
2 0
0.002 x
x2 l
2l
l
2 103 m 3
2
Page
29
作业
6-1 6-3 6-8 A-8
Page
30
§6-3 对称弯曲切应力
解：1. 问题分析
已知=(D+d)/2, E, 截面尺寸，可应

材料力学第6章弯曲应力


页 退出
材料力学
出版社 理工分社
图6.3 依据上述分析，弯曲变形可描述为横截面绕各自中性轴的轻微转动。由于梁 上的载荷都作用于梁的纵向对称面内，所以梁的整体变形应对称于纵向对称 面，这就要求中性轴与纵向对称面垂直。
页 退出
材料力学
出版社 理工分社
6.2.2纯弯曲正应力 纯弯曲时横截面上只有正应力，全部正应力的合力应该等于该横截面上的弯 矩。由于纯弯曲时梁横截面上正应力的分布规律未知，因此，不能直接由弯 矩M来确定正应力σ 。和推导圆轴扭转剪应力计算公式相似，需要从研究构 件的变形入手，综合考虑变形几何关系、物理关系以及静力平衡关系，才能 得到纯弯曲时的正应力。
其中，A点处为最大压应力，D点处为最大拉应力，B点处为拉应力。
页 退出
材料力学
对于Ⅱ—Ⅱ截面，弯矩MⅡ=20-15×3=-25 kN·m，所以
出版社 理工分社
其中，A点处为最大拉应力，D点处为最大压应力，B点处为压应力。
页 退出
材料力学
出版社 理工分社
例6.2如图6.7(a)所示简支梁，由56a号工字钢制成，其截面简 化后的尺寸如图6.7(b)所示。已知集中力F=150 kN。试求梁危 险截面上的最大正应力和同一截面上翼缘与腹板交界处a 点( 见图6.7(b))的正应力。
页 退出
材料力学
出版社 理工分社
6.3弯曲剪应力 横力弯曲的梁横截面上既有弯矩又有剪力，因此，横截面 上既有正应力又有剪应力。弯曲剪应力分布较复杂，截面 形状不同，分布规律也不相同。下面讨论几种常用的对称 截面梁横截面上的弯曲剪应力。
页 退出
材料力学
出版社 理工分社
6.3.1矩形截面梁 如图6.8(a)所示矩形截面梁的任意截面上，剪力Q皆与截面的对称轴y重合( 见图6.8(a))。关于横截面上剪应力的分布规律，作以下两个假设：①横截 面上各点的剪应力的方向都平行于剪力Q；②剪应力沿截面宽度均匀分布。 在截面高度h大于宽度b的情况下，以上述假设为基础得到的解，与精确解相 比有足够的准确度。按照这两个假设，在距中性轴为y的横线pq上，各点的 剪应力 都相等，且都平行于Q。再由剪应力互等定理可知，在沿pq切出的 平行于中性层的pr平面上，也必然有与相等 的 ′，而且 ′沿截面宽 度也是均匀分布的(见图6.8(d))。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第六章 弯曲应力1 基本概念及知识要点1.1 基本概念纯弯曲、横力弯曲、弯曲正应力、惯性矩、抗弯截面系数、弯曲刚度、弯曲切应力（剪应力）。

应熟练理解和掌握这些基本概念。

1.2 平面弯曲工程实际中的梁，大多数是具有一个纵向对称面的等截面直梁。

外载荷作用在梁的纵向对称面内，并垂直于梁的轴线，梁弯曲时轴线将在对称平面内弯曲成平面曲线，这种弯曲叫平面弯曲。

当梁横截面上既有弯矩又有剪力时，梁的弯曲是横力弯曲（或剪切弯曲）；梁横截面上只有弯矩而没有剪力时，梁的弯曲是纯弯曲。

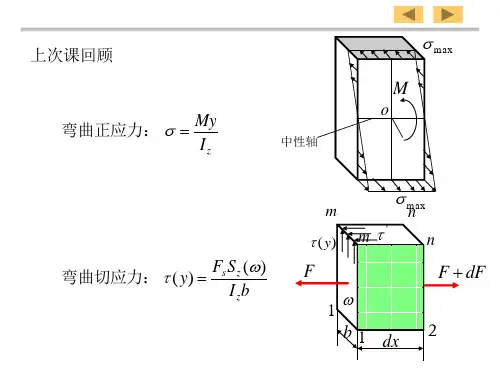
1.3 弯曲正应力梁在纯弯曲时的正应力是综合运用变形几何关系、物理关系和静力平衡关系推导出来的，推导弯曲正应力公式的方法，与推导轴向拉压正应力公式和扭转切应力公式的方法相同。

弯曲正应力公式zI My=σ 式中M 为所研究截面的弯矩；z I 分为截面图形对中性轴的惯性矩；y 为所求应力点到中性轴的距离。

计算时，M 和y 均用代数值代入，由此得到所求点的应力符号，同样也可根据梁的变形情况来确定。

梁弯曲正应力公式适用材料处于线弹性范围内的纯弯曲梁，可推广到横力弯曲以及小曲率杆的弯曲中。

1.4 弯曲切应力弯曲切应力公式的推导不是按照变形几何关系、物理关系、平衡关系三方面进行的，而是根据分析对弯曲切应力的分布规律作出假定——平行于剪力F s 且沿截面厚度均匀分布，然后利用平衡关系直接导出矩形截面切应力公式*zzF S bI τ=s 式中，F s 为截面上的剪力；z I 为整个截面对中性轴的惯性矩；b 为所求切应力处横截面的宽度；*z S 为截面上距中性轴为y 的横线任一侧部分面积对中性轴的静矩。

1.5 弯曲强度条件1 正应力强度条件弯曲正应力是影响梁强度的主要因素，对梁（等截面梁）的强度计算主要是满足正应力强度条件][maxmax σσ≤=zW M 式中maxy I W zz =称为横截面的抗弯截面系数。

对于塑性材料，其抗拉和抗压能力相等，通常将梁设计为与中性轴对称的形状，强度条件为][maxmax σσ≤=zW M 对于脆性材料，其抗压能力远超过抗拉能力。

通常将梁设计为与中性轴不对称的形状，使中性轴偏向受拉一侧（请读者思考为什么？）。

强度条件为max 1max []z M y I σσ=≤t t max 2max []zM y I σσ=≤c c 2 切应力强度条件对薄壁截面（例如工字型、槽型等）梁，有时需要校核弯曲切应力强度条件*max max ()[]z zF S bI ττ=≤smax τ一般发生在中性轴处，因此max *)(z S 为中性轴以下（或以上）面积对中性轴的静矩。

1.6 弯曲中心的概念当横向力作用平面平行于开口薄壁杆件的形心主惯性平面且通过某一特定点时，杆件只发生弯曲变形而不发生扭转变形，这一点称为开口薄壁杆件的弯曲中心。

弯曲中心只与截面的几何形状及尺寸有关，具有对称轴的截面的弯曲中心必然在对称轴上。

2 重点与难点及解析方法2.1 弯曲正应力的计算平面弯曲时，既不伸长也不缩短的轴叫中性轴，中性轴通过截面的形心。

横截面上的弯曲正应力呈线性分布，最大弯曲正应力发生在距离中性轴最远的点上。

解析方法：中性轴通过截面的形心的结论，是在轴力为零及材料拉压弹性模量相等的情况下得出的，否则中性轴将偏移，此时应由轴向力平衡方程求中性轴的位置。

2.2 梁的弯曲强度计算梁的弯曲强度计算是材料力学的重要问题，应通过大量不同类型的弯曲强度计算熟练掌握。

解析方法：1.根据梁所受载荷及约束力，正确画出梁的剪力图和弯矩图，确定s max F 和maxM作用面，即危险截面。

2. 根据截面上的应力分布，判断危险截面上的危险点，即max σ和max τ作用点（注意二者不一定在同一截面，更不在同一点），并计算max σ和max τ数值。

3． 对max σ和max τ作用点分别采用不同的强度条件进行强度计算。

对于细长梁，正应力与切应力相比，正应力对强度的影响是主要的。

因此一般只需按正应力进行强度计算。

只有当某些受力情形下，个别截面上的剪力较大时，才考虑切应力的强度。

在应用强度条件进行梁的截面设计时，一般先按正应力强度条件选择截面，然后再进行切应力强度校核。

2.3 提高梁弯曲强度的途径弯曲正应力公式可变形为][][max M W M z =≤σ，式左侧为由载荷引起的最大弯矩；式右侧为构件的许用弯矩，它与两个因素y W 和][σ有关。

所以提高构件的弯曲强度有两种：减小max M ；提高y W 和][σ。

3 典型问题解析例题6.1：一铸铁梁的受力如图6－1（a大弯曲正应力。

解：1 求约束反力并作内力图由平衡方程求得 3.5k N A F =R 13.5k NB F =R 图6－1作梁的弯矩图如图6－1（c ）所示。

max 5kN m M =⋅，发生在B 截面处。

2 计算截面的几何性质量（b ）图中y 轴为对称轴。

选择截面上边缘为参考坐标轴1z ，确定形心C 的位置。

802010201208052mm 802020120C y ⨯⨯+⨯⨯==⨯+⨯通过形心C 的y 、z 轴为形心主轴，z 为中性轴。

求形心主惯性矩z I 。

3232641(8020802042)121(201202012028)7.6410mm 12z I =⨯⨯+⨯⨯+⨯⨯+⨯⨯=⨯3 求梁内的最大正应力本例由于梁的截面上、下不对称，所以最大正弯矩的作用截面C 和最大负弯矩的作用截面B 均可能是危险截面。

最大拉应力发生在C 截面下边缘的各点处，其值为632max63.510881040.3MPa 7.6410C z M y I σ--⨯⨯⨯===⨯t 最大压应力发生在B 截面下边缘的各点处，其值为632max6510881057.6MPa 7.6410B z M y I σ--⨯⨯⨯===⨯c 解题指导：解此类题的关键是确定危险截面及组合截面的惯性矩。

由弯曲内力图确定危险截面，特别注意对于由脆性材料制成的不对称截面梁，最大拉应力与最大压应力的点可能不在同一截面上，应仔细验算弯矩最大截面及弯矩较大截面上的弯曲正应力。

例题6.2：外伸梁的截面尺寸及受力如图6－2（a ）所示，求梁内最大弯曲正应力。

解：1．作弯矩图确定危险截面剪力图、弯矩图分别如图6－2（b ）、（c ）所示，从图6－2（c ）中可得max 20kN m M =⋅图6－22．计算组合截面的惯性矩图示组合截面，具有两根对称轴，形心很容易确定，通过形心垂直于加力方向的y 轴即为中性轴。

采用负面积法，得()()34333342001020010π1610π12641264y bh dI ---⨯⨯⨯⨯⨯=-=-444413321003221010110m ...---=⨯-⨯=⨯ 3．计算最大正应力maxmaxmax 334201010010198MPa10110yMz I ..σ--=⨯⨯⨯==⨯解题指导：计算组合截面的惯性矩，常用的是利用平行移轴公式计算，详见第五章，有时可用负面积法。

例题6.3：T 形截面铸铁梁如图6－3（a ）所示。

若kN 42P ＝F ，截面对形心轴z 的惯性矩4cm 10180=z I ，cm 36.15cm, 64.921==y y 材料[] MPa 40t =σ,[] MPa 160c =σ，试按正应力强度条件校核该梁的强度。

解:1. 作梁的弯矩图，确定危险截面梁的弯矩图如图6－3（b ）所示，在固定端处有最大正弯矩kNm 60.33=A M2. 根据正应力强度条件校核梁的固定端截面：固定端截面沿高度方向正应力的分布规律如图6－3（c ）所示，在下边缘a 点有拉应力的极值：[]t 8231 M P a 8.3110101801064.9106.33σσ≤=⨯⨯⨯⨯==--Z A a I y M 在上边缘b 点有压应力的极值：[]c Z A b I y M σσ≤=⨯⨯⨯⨯==-- M P a 70.5010101801036.15106.338232 3. 在B 截面处有最大的负弯矩25.2kN m B M ⋅＝ ，B 截面上正应力分布规律如图6－3（d ）所示。

由于12y y <，截面的上边缘e 点有可能成为危险点，出现全梁最大的拉应力。

因此还需对e 点的正应力进行校核。

[]t 8232 MPa 02.3810101801036.15102.25σσ≤=⨯⨯⨯⨯==--Z C e I y M通过以上计算可知，当梁的截面中性轴不是对称轴，且最大正弯矩和最大负弯矩都较大时，max t σ和max c σ可能不在同一截面上，需同时校核所有可能成为危险点的地方。

解题指导：明确分析弯曲强度问题的计算步骤：外力——内力——危险截面（max M 、max F s ）——危险截面上的应力分布——危险点的应力及图6－3其应力状态——强度条件。

例题6.4： 外伸梁受力如图6－4（a ）所示。

梁由钢板焊接而成，截面尺寸如图6－4（b ）所示。

已知[]120=σMPa ，[]60=τMPa ，试校核梁的强度，并求焊缝ab 处的切应力。

解：1 求约束反力并作内力图由平衡方程求得 R 25kN A F =，R 105kN B F =s F 梁的剪力图和弯矩图分别如图6－4（c ）、（d ）所示。

s max 65kN F =，发生在B 左截面处。

max 40kN m M =⋅，发生在B 截面处。

2 计算截面的几何性质同例题6.1类似的方法可求得确定形心C 的位置100201022002010082mm 10020220020C y ⨯⨯+⨯⨯⨯==⨯+⨯⨯组合图形的形心主惯性矩z I3232741(100201002072)1212(202002002018) 3.9710mm 12z I =⨯⨯+⨯⨯+⨯⨯⨯+⨯⨯=⨯3 强度校核沿B 截面高度方向正应力的分布如图6－4（e ）所示，最大正应力发生在截面的下边缘处，[]33maxmax max 5401011810118.9MPa 3.9710< zM y I σσ--⨯⨯⨯===⨯ 沿B 左截面的高度切应力分布如图6－4（f ）所示，最大切应力发生在中性轴处，图6－4*53max 1)220118118 2.7510mm 2z S =⨯⨯⨯⨯=⨯（[]*35s maxmax max 7()6510 2.751011.4MPa 220 3.9710< z zF S bI ττ⨯⨯⨯===⨯⨯⨯ 故此梁安全。

4 求焊缝ab 处的切应力在焊缝ab 处将截面截为两部分，求出其任一部分（例如左部分）对中性轴z 的静矩：4*102.71820200⨯=⨯⨯=z S mm 3 *34s 765107.210 5.9MPa 20 3.9710z ab z F S bI τ⨯⨯⨯===⨯⨯解题指导：弯曲切应力公式中，s F 、z I 对一个确定截面而言为不变量，它们均与所求应力点的位置无关。