第六章扭转与弯曲的强度计算

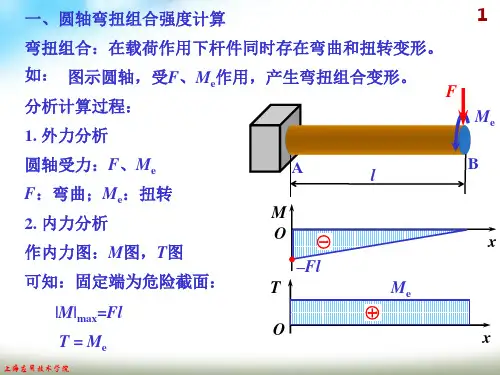
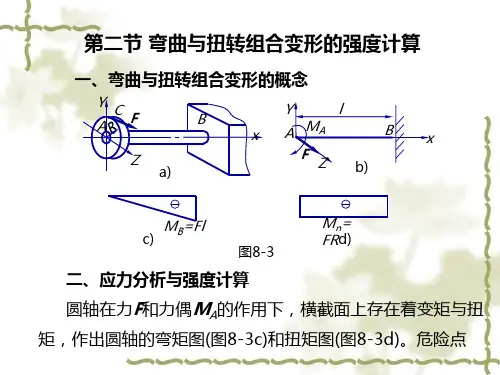
第六章组合变形一．内容•组合变形的概念和危险点的应力状态。

•用叠加法计算拉伸(压缩)与弯曲组合、偏心拉压、斜弯曲的应力，用平面应力分析理论计算弯扭组合的应力。

•实验内容：弯扭组合梁电测实验，复杂应力状态下应力测试技术。

二．学习目标学完本章后，学生能够：•掌握组合变形的一般求解方法。

•熟练掌握拉伸(压缩)与弯曲、斜弯曲、偏心拉压、扭转与弯曲组合变形的概念和强度计算。

•了解截面核心概念和计算。

•学会弯扭组合梁的电测实验操作步骤。

三．重点和难点重点：采用叠加原理和平面应力分析理论计算拉（压）弯组合、斜弯曲、弯扭组合的最大应力，并进行强度校核。

难点：杆件组合变形下危险截面和危险点的确定；拉伸（压缩）和弯曲、和扭转组合时的强度校核。

四．学习建议1.无论何种形式的组合变形，首先将几组载荷分解成若干基本载荷，分别计算各基本载荷引起杆件横截面上的应力，然后进行叠加，当应力平行时，则求其代数和，否则（如正应力和切应力）将根据平面应力分析计算截面最大应力。

分析和求解组合变形习题的关键是分与合。

分，就是将同时作用的几组载荷分解成若干基本载荷，并分别计算杆件的应力。

合，则是将各基本变形引起的应力叠加起来，但不是简单的代数相加，而应是同一截面正应力或切应力矢量和，当应力平行时，则应是求其代数和，故应注意应力的方向。

这种分析方法适用于各种基本变形的组合变形，在学习时应注意分析方法和步骤，具体问题具体分析，不必强记一些计算公式。

在使用时要注意条件，如扭弯组合变形的强度条件适用于圆截面轴，虽然对非圆截面轴公式不再适用，但分析方法仍然与圆截面轴相同。

2.处理组合变形问题的方法，学习时应着意领会方法的实质，而不要只是记住有关的公式，因为组合变形问题是多种多样的，但处理原则是一致的。

如圆截面杆除承受弯扭组合变形外，同时还承受轴向拉（压）变形，按照以上处理原则，可以写出其强度条件为3.组合变形下，若危险点处为单向应力状态时，叠加只是一种代数运算；若危险点处为复杂应力状态时，叠加将是应力状态的叠加，其强度问题应使用适当的强度理论。

灌南中专教师授课教案2018 /2019 学年第一学期课程汽车机械基础教学内容旧知复习：1.圆轴扭转的概念。

2.圆轴扭转的外力偶矩、扭矩的计算方法。

3.圆轴扭转的强度计算方法。

讲授新课：第六章材料力学基础第5节直梁的弯曲一、平面弯曲的概念1. 平面弯曲在工程实际中，把发生弯曲变形为主的构件称为梁，如跨江大桥两桥墩之间的横梁、汽车前梁等。

梁在自重和载荷的作用下会产生平面弯曲变形。

梁弯曲变形的受力特点：外力垂直于轴线或在轴线的平面内受到力偶的作用。

变形的特点：轴线在纵向对称平面内由直线弯曲成曲线。

2. 梁的基本类型根据支座对梁的约束，将梁简化为三种基本形式。

（1）简支梁梁的两端均用铰链支座约束，一端为固定铰链支座，另一端为活动铰链支座，如图6-26a所示。

（2）外伸梁简支梁的一端（或两端）伸出支座以外，如图6-26b所示。

（3）悬臂梁梁的一端为固定支座，另一端为自由端，如图6-26c所示。

3.载荷的简化作用在梁上的载荷可简化为以下三种形式。

（1）集中力集中力是将作用于梁上方的长度很短的力简化为作用于一点的力，单位为N或kN。

（2）集中力偶矩集中力偶矩是将作用于梁上方的长度很短的力偶矩简化为作用于某一截面的集中力偶矩，单位为N·m或kN·m。

（3）分布载荷分布载荷是指沿梁的长度或部分长度连续均匀分布的载荷，称为分布载荷。

单位长度上的力用q表示，称集度载荷，单位为N/m或kN/m。

二、梁弯曲变形的内力1.用截面法求梁的内力为了计算梁的强度，必须研究梁上各截面上的内力，分析内力和计算内力的方法仍旧采用截面法。

例6-8剪力和弯矩的大小、方向或转向的确定原则如下：（1）截面上剪力的大小等于此截面以左（或右）所有外力的代数和。

截面左侧的外力，向上取正号，向下取负号。

截面右侧的外力与此相反。

（2）截面上弯矩的大小等于此截面以左（或右）所有外力对该截面形心的力矩的代数和。

截面左侧的外力对截面形心的力矩顺时针转向为正，反之为负。

扭转强度计算公式
扭转强度是指材料可以承受持续转变外力的能力，它也是衡量材料结构强度的一个重要指标。

由于它对于确定材料性能及其结构安全性起着重要作用，因此了解扭转强度和计算其值非常重要。

扭转强度的计算可以通过以下公式来实现：T=F * r / J，其中T为扭转强度，F为外力，r为外力的作用半径，J为扭转截面积矩，即材料主轴线上的横截面积。

通过上述公式可以看出，要计算扭转强度，必须先确定外力F和扭转截面积矩J的大小。

外力F是指作用在材料上的外力，可以通过实验来确定。

而扭转截面积矩J是指材料的横截面积，可以通过实验或理论计算来确定。

在实际应用中，扭转强度的计算还受到水平和垂直外力的影响，因此，在计算扭转强度时，必须考虑外力的方向和强度。

在计算扭转强度时还要考虑材料的尺寸、形状和结构，以及外力的作用点。

这些因素都会影响材料的扭转强度，因此，在计算扭转强度时，必须将这些因素考虑在内。

要计算材料扭转强度，必须先确定外力F和扭转截面积矩J，还要考虑材料尺寸、形状和结构以及外力方向和强度等因素。

通过恰当的计算，可以准确地测量出材料的扭转强度，从而为结构的安全性
提供可靠的参考。

组合变形的强度计算 组合变形的概念拉伸与弯曲的组合一.组合变形的概念1.组合变形:在外力的作用下，构件若同时产生两种或两种以上基本变形的情况在小变形和线弹性的前提下，可以采用叠加原理研究组合变形问题所谓叠加原理是指若干个力作用下总的变形等于各个力单独作用下变形的总和（叠加）在复杂外载作用下，构件的变形会包含几种简单变形PRzxyPP2、组合变形的研究方法——叠加原理叠加原理应用的基本步骤：①外力分析：将载荷进行分解，得到与原载荷等效的几组载荷，使构件在每一组载荷的作用下，只产生一种基本变形.②内力分析：分析每种载荷的内力，确定危险截面.③应力分析：分别计算构件在每种基本变形情况下的危险将各基本变形情况下的应力叠加，确定最④强度计算:二.弯曲与拉伸(的组合杆件在外力作用下同时产生弯曲和拉伸（压缩）变形称为弯曲与拉伸（压缩）的组合偏心拉伸:弯曲与拉伸的组合变形链环受力立柱受力拉伸与弯曲组合的应力分析ϕϕsin p p cos p p y x ==A P x ='σy I M x l P M zy =''-=σ)(作用下：z T W M A N max max +=σzC W M A N max max -=σ危险截面处的弯矩抗弯截面模量y I M A N z +=''+'=σσσ根据叠加原理，可得x 横截面上的总应力为[]T z max max T W M A N σσ≤+=[]c zmax max C W M A N σσ≤-=强度条件为例:悬臂吊车,横梁由25 a 号工字钢制成，l =4m ，电葫芦重Q 1=4kN ，起重量Q2=20kN , α=30º, [σ]=100MPa，试校核强度。

取横梁AB为研究对象，受力如图b所示。

梁上载荷为P =Q1+Q2= 24kN，斜杆的拉力S 可分解为X B和Y B（1）外力计算横梁在横向力P和Y A、Y B作用下产生弯曲；同时在X A和X B作用下产生轴向压缩。

扭转的强度条件—例题分析例题1-1 一电机传动钢轴，直径d = 40mm ，轴传递的功率30kW ，转速n = 1400r/min 。

轴的许用切应力[]τ= 40MPa ，试校核此轴的强度。

解：（1）计算扭力偶矩和扭矩。

扭力偶距为x m = 9550n P = 9550140030⨯= 204×103 （N ·mm ） 由截面法求得轴横截面上的扭矩为：320410(N mm)x T m ==⨯⋅(2) 强度校核。

轴的抗扭截面系数为 334320 1.25510(mm )22R W ρππ⨯===⨯3maxmax 42041016.3(MPa)1.25510T W ρτ⨯==⨯ 因为 max []40(MPa)ττ<=轴满足扭转强度条件。

例题1-2 如图所示为汽车传动轴简图，轴选用无缝钢管，其外半径45mm R =，内半径42.5mm r =。

许用剪应力[]τ=60MPa ，根据强度条件，求轴能承受的最大扭矩。

例题1-2图解：按强度条件确定最大扭矩。

42.50.94445r R α=== 3344345(1)(10.944)29400(mm )22R W ρππα⨯=-=-=由强度条件得3max []6029400176410(N mm)1764(N m)T W ρτ≤=⨯=⨯⋅=⋅轴能承受的最大扭矩为1764N m ⋅。

例题1-3 某传动轴，轴内的最大扭矩max 1.5kN m T =⋅，若许用切应力[]τ=50MPa ，试按下列两种方案确定轴的横截面尺寸，并比较其重量。

①实心圆截面轴；②空心圆截面轴，其内、外半径的比值9.022=R r 。

解：（1）确定实心圆轴的半径。

根据强度条公式可得 max T W ρτ≥ 将实心圆轴的抗扭截面系数32R W ρπ=代入上式得126.73(mm)R ≥= 取 )(271mm R =（2）确定空心圆轴的内、外半径。

将空心圆轴的抗扭截面系数()3412R W ρπα=-代入强度条件式可得238.15(mm)R = 其内半径相应为220.90.938.1534.34(mm)r R ==⨯=取 239(mm)R = 234(mm)r =（3）重量比较。

弯扭合成强度计算公式
弯扭合成强度计算公式是用于评估材料在受到弯曲和扭转同时作用时的强度。

该公式用于工程领域，尤其是在设计和制造结构件时非常重要。

通过计算弯扭合成强度，工程师可以确定材料的可靠性并确保结构的安全运行。

弯扭合成强度计算公式如下：
σc = √((σb^2) + (τ^2))
其中：
- σc表示弯扭合成强度；
- σb表示弯曲应力；
- τ表示扭转应力。

弯曲应力是由受力物体的内部应力分布产生的，是垂直于截面剪切应力的一个力，常用弯曲矩I和截面模量W计算。

扭转应力是由物体在扭转时所受到的应力，产生于物体截面上的切应力。

弯扭合成强度计算公式的主要思想是将弯曲和扭转应力分量合成为一个等效应力。

这是因为弯曲和扭转会在结构件中同
时产生，可能引起材料破坏。

通过计算并比较弯扭合成强度和材料的强度极限，可以确定结构件是否足够强固以承受外部载荷。

需要注意的是，弯扭合成强度计算公式是根据特定假设和
理论推导得出的，只能用于特定条件下的工程计算。

在实际工程中，还需考虑其他因素，如材料的疲劳性能、环境影响和设计安全系数等。

因此，在进行结构设计时，工程师应综合考虑各种因素，并根据具体情况进行适当调整。

总之，弯扭合成强度计算公式是工程设计中重要的工具，
帮助工程师评估材料的强度。

准确计算弯曲和扭转应力，并合成为弯扭合成强度，能够确保结构件的安全可靠性。

然而，在应用公式时需要注意其适用条件，并对其他因素进行综合考虑，以保证设计的合理性和可靠性。