材料力学06(第六章 弯曲应力)分析
- 格式:ppt
- 大小:2.52 MB
- 文档页数:11


材料力学梁的应力解读
梁是结构分析中最基本的问题之一,也是材料力学中一个重要的概念。
梁的应力解读,就是对梁结构中的应力的分析。
一般来说,在材料力学中,梁的应力解读可以从下面几个方面来进行:
(1)弯曲应力:弯曲应力是指当梁在受到外力的作用下发生偏移或
沿着其中一轴线变形时,梁中钢材筋的纵向应力称为弯曲应力。
根据梁的
预定约束方式,可以分为受自重弯曲的应力和受外力弯曲的应力。
受自重
弯曲的应力大小由梁的自重和梁的几何形态所决定,一般情况下,斜梁的
自重弯曲应力会比悬臂梁的自重弯曲应力大。
受外力弯曲的应力大小取决
于受力梁的拉张性和刚度,以及施加外力的位置,大小和作用方向等因素,其中最重要的是材料的弹性模量。
(2)剪切应力:梁结构的剪切应力,是指梁受到外力作用时,对面
两侧的钢材筋之间的剪切应力。
由于受力面两端受非对称分布的外力作用,使得受力面的梁结构受到剪切应力的作用,一般情况下,受力面梁结构分
布的剪切应力会在受力面的两端有最大值,随着回头距离变小而逐渐减小。
(3)压应力:梁受外力所产生的压应力,是指受力面角支撑点处承
受拉力的钢材筋之间的应力,称为压应力。





需要课件请或弯曲变形粱的挠度与转角(一)挠曲线在外力作用下,梁的轴线由直线变为光洁的弹性曲线,梁弯曲后的轴线称为挠曲线。
在平面弯曲下,挠曲线为梁形心主惯性平面内的一条平面曲线v=f(x)(见图5-8-1)。
(二)挠度与转角梁弯曲变形后,梁的每一个横截面都要产生位移,它包括三部分:1. 挠度梁横截面形心在垂直于轴线方向的线位移,称为挠度,记作v。
沿梁轴各横截面挠度的变化规律,即为梁的挠曲线方程。
v=f(x)2.转角横截面相对本来位置绕中性轴所转过的角度,称为转角,记作θ。
小变形情况下,3.此外,横截面形心沿梁轴线方向的位移,小变形条件下可忽略不计。
(三)挠曲线近似微分方程在线弹性范围、小变形条件下,挠曲线近似微分方程为上式是在图5—8—l所示坐标系下建立的。
挠度w向下为正,转角θ顺时针转为正。
积分法计算梁的位移按照挠曲线近似微分方程(5—8—1),积分两次,即得梁的转角方程和挠度方程,即由第1 页/共6 页式中积分常数C、D,可由梁的边界条件来决定。
当梁的弯矩方程需分段列出时,挠曲线微分方程也需分段建立,分段积分。
于是全梁的积分常数数目将为分段数目的两倍。
为了决定所有积分常数,除利用边界条件外,还需利用分段处挠曲线的延续条件(在分界点处左、右两段梁的转角和挠度均应相等)。
用叠加法求梁的位移(一)叠加原理几个荷载同时作用下梁的任一截面的挠度或转角等于各个荷载单独作用下同一截面挠度或转角的总和。
(二)叠加原理的适用条件叠加原理仅适用于线性函数。
要求挠度、转角为梁上荷载的线性函数,必须满意: 1.材料为线弹性材料;2.梁的变形为小变形;3.结构几何线性。
(三)叠加法的特征1.各荷载同时作用下挠度、转角等于单独作用下挠度、转角的总和,应该是几何和,同一方向的几何和即为代数和。
2.梁在容易荷载作用下的挠度、转角应为已知或可查手册。
3.叠加法相宜于求梁某一指定截面的挠度和转角。
[例 5—8—1] 用积分法求图5—8—3所示各梁的挠曲线方程时,试问应分为几段?将浮上几个积分常数? 并写出各梁的边界条件和延续条件。

材料⼒学习题第六章应⼒状态分析答案详解第6章应⼒状态分析⼀、选择题1、对于图⽰各点应⼒状态,属于单向应⼒状态的是(A )。
20(MPa )20d20(A )a 点;(B )b 点;(C )c 点;(D )d 点。
2、在平⾯应⼒状态下,对于任意两斜截⾯上的正应⼒αβσσ=成⽴的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC ⾯上只作⽤有切应⼒τ,现关于AC ⾯上应⼒有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==;(B )AC AC /2,/2ττσ==;(C )AC AC /2,/2ττσ==;(D )AC AC /2,/2ττσ=-=。
4、矩形截⾯简⽀梁受⼒如图(a )所⽰,横截⾯上各点的应⼒状态如图(b )所⽰。
关于它们的正确性,现有四种答案,正确答案是( D )。
(b)(a)(A)点1、2的应⼒状态是正确的;(B)点2、3的应⼒状态是正确的;(C)点3、4的应⼒状态是正确的;(D)点1、5的应⼒状态是正确的。
5、对于图⽰三种应⼒状态(a)、(b)、(c)之间的关系,有下列四种答案,正确答案是( D )。
τ(a) (b)(c)(A)三种应⼒状态均相同;(B)三种应⼒状态均不同;(C)(b)和(c)相同;(D)(a)和(c)相同;6、关于图⽰主应⼒单元体的最⼤切应⼒作⽤⾯有下列四种答案,正确答案是( B )。
(A) (B) (D)(C)解答:maxτ发⽣在1σ成45o的斜截⾯上7、⼴义胡克定律适⽤范围,有下列四种答案,正确答案是( C )。
(A)脆性材料;(B)塑性材料;(C)材料为各向同性,且处于线弹性范围内;(D)任何材料;8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适⽤于( C )。


材料力学弯曲应力材料力学是研究材料在外力作用下的变形和破坏规律的一门学科,而弯曲应力是材料在受到弯曲载荷时所产生的应力。
弯曲应力的研究对于工程结构设计和材料选用具有重要意义。
本文将从弯曲应力的概念、计算公式、影响因素等方面进行详细介绍。
弯曲应力是指在材料受到弯曲载荷作用下,横截面上的应力分布情况。
在弯曲过程中,材料上部受到压应力,下部受到拉应力,而中性面则不受应力影响。
根据梁的理论,弯曲应力与弯矩、截面形状以及材料性质有关。
在工程实践中,我们通常使用梁的弯曲应力公式来计算弯曲应力的大小。
梁的弯曲应力公式可以表示为:\[ \sigma = \frac{M \cdot c}{I} \]其中,σ为弯曲应力,M为弯矩,c为截面中性轴到受拉或受压纤维的距离,I为截面的惯性矩。
从公式中可以看出,弯曲应力与弯矩成正比,与截面形状和材料性质有关,截面越大,惯性矩越大,弯曲应力越小。
影响弯曲应力的因素有很多,主要包括载荷大小、截面形状、材料性质等。
首先是载荷大小,当外力作用在梁上时,产生的弯矩大小将直接影响弯曲应力的大小。
其次是截面形状,截面形状不同将导致截面惯性矩不同,进而影响弯曲应力的大小。
最后是材料性质,材料的弹性模量、屈服强度等参数也会对弯曲应力产生影响。
在工程实践中,我们需要根据具体的工程要求和材料性质来选择合适的截面形状和材料类型,以使得结构在受到弯曲载荷时能够满足强度和刚度的要求。
同时,还需要合理设计结构,减小弯曲应力集中的区域,避免出现应力集中而导致的破坏。
综上所述,弯曲应力是材料在受到弯曲载荷时产生的应力,其大小与弯矩、截面形状和材料性质有关。
在工程实践中,我们需要根据具体的工程要求和材料性质来计算和分析弯曲应力,以保证结构的安全可靠。
同时,合理设计结构和选择合适的材料也是降低弯曲应力的重要手段。
希望本文对于弯曲应力的理解和应用能够有所帮助。
第六章 弯曲应力1 基本概念及知识要点1.1 基本概念纯弯曲、横力弯曲、弯曲正应力、惯性矩、抗弯截面系数、弯曲刚度、弯曲切应力(剪应力)。
应熟练理解和掌握这些基本概念。
1.2 平面弯曲工程实际中的梁,大多数是具有一个纵向对称面的等截面直梁。
外载荷作用在梁的纵向对称面内,并垂直于梁的轴线,梁弯曲时轴线将在对称平面内弯曲成平面曲线,这种弯曲叫平面弯曲。
当梁横截面上既有弯矩又有剪力时,梁的弯曲是横力弯曲(或剪切弯曲);梁横截面上只有弯矩而没有剪力时,梁的弯曲是纯弯曲。
1.3 弯曲正应力梁在纯弯曲时的正应力是综合运用变形几何关系、物理关系和静力平衡关系推导出来的,推导弯曲正应力公式的方法,与推导轴向拉压正应力公式和扭转切应力公式的方法相同。
弯曲正应力公式zI My=σ 式中M 为所研究截面的弯矩;z I 分为截面图形对中性轴的惯性矩;y 为所求应力点到中性轴的距离。
计算时,M 和y 均用代数值代入,由此得到所求点的应力符号,同样也可根据梁的变形情况来确定。
梁弯曲正应力公式适用材料处于线弹性范围内的纯弯曲梁,可推广到横力弯曲以及小曲率杆的弯曲中。
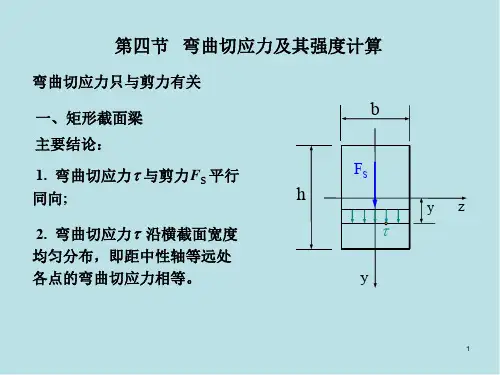
1.4 弯曲切应力弯曲切应力公式的推导不是按照变形几何关系、物理关系、平衡关系三方面进行的,而是根据分析对弯曲切应力的分布规律作出假定——平行于剪力F s 且沿截面厚度均匀分布,然后利用平衡关系直接导出矩形截面切应力公式*zzF S bI τ=s 式中,F s 为截面上的剪力;z I 为整个截面对中性轴的惯性矩;b 为所求切应力处横截面的宽度;*z S 为截面上距中性轴为y 的横线任一侧部分面积对中性轴的静矩。
1.5 弯曲强度条件1 正应力强度条件弯曲正应力是影响梁强度的主要因素,对梁(等截面梁)的强度计算主要是满足正应力强度条件][maxmax σσ≤=zW M 式中m axy I W zz =称为横截面的抗弯截面系数。
对于塑性材料,其抗拉和抗压能力相等,通常将梁设计为与中性轴对称的形状,强度条件为][maxmax σσ≤=zW M 对于脆性材料,其抗压能力远超过抗拉能力。
6.1. 矩形截面悬臂梁如图所示,已知l =4m , b /h =2/3,q =10kN/m ,[σ]=10MPa ,试肯定此梁横截面的尺寸. 解:(1) 画梁的弯矩图由弯矩图知:(2) 盘算抗弯截面系数32323669h bh h W ===(3) 强度盘算22maxmax 33912[]29416 277ql M ql h Wh h mm b mmσσ===⋅≤∴≥==≥6.2. 20a 工字钢梁的支承和受力情形如图所示,若[σ]=160MPa ,试求允许载荷.解:(1)画梁的弯矩图(2) 查表得抗弯截面系数6323710W m -=⨯(3) 强度盘算max max 66223[]33[]3237101601056.8822PM P W W WW P kNσσσ-===⋅≤⨯⨯⨯⨯∴≤==取允许载荷No20ax ql x[]57P kN =6.3. 图示圆轴的外伸部分系空心轴.试作轴弯矩图,并求轴内最大正应力.解:(1)(2) C 截面:3max3332 1.341063.20.0632C C C C C M M MPa d W σππ⨯⨯====⨯B 截面:3max3434440.91062.10.060.045(1)(1)32320.06B B B BB B B M M MPa D d W D σππ⨯====⨯--(3) 轴内的最大正应力值MPa C 2.63max max ==σσ6.5.把直径d =1m 的钢丝绕在直径为2m 的卷筒上,设E =200GPa,试盘算钢丝中产生的最大正应力. 解:(1) 由钢丝的曲率半径知1M E M EI I ρρ=∴=(2) 钢丝中产生的最大正应力93max200100.510100 1MR ER MPa I σρ-⨯⨯⨯====6.8. 压板的尺寸和载荷如图所示.材料为45钢,σs =380MPa ,取安全系数n=1.5.试校核压板的强度.x解:(1)(2) 232363330.030.0212(1)(1) 1.568106620bH hW m H -⨯=-=-=⨯(3) 强度盘算许用应力380[]2531.5SMPa nσσ===强度校核max 6308196[]1.56810A M MPa W σσ-===⨯压板强度足够.6.12.图示横截面为⊥形的铸铁推却纯曲折,材料的拉伸和紧缩许用应力之比为[σt ]/[σc ]=1/4.求程度翼缘的合理宽度b .解:(1) ,max 11320 c c y mm=(2) 由截面形心地位()()304006017060370320304006060510 i CiC iA y b y Ab b mm⨯-⨯+⨯⨯===⨯-+⨯=∑∑6.13. ⊥形截面铸铁梁如图所示.若铸铁的许用拉应力为[σt ]=40MPa ,许用压应力为[σc ]=4P . 解:(1)(2) A ()22max 86320.8[][]101801016010132.60.80.825096.410A C C zC zCzC C M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯A 截面的最大拉应力11max 86310.8[][]1018010401052.80.80.896.410A t t zC zCzC t M h Ph I I I P kNh σσσ--==≤⨯⨯⨯∴≤==⨯⨯C 截面的最大拉应力()22max 86320.6[][]1018010401044.20.60.625096.410C t t zC zCzC t M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯取许用载荷值[]44.2P kN =6.14. 铸铁梁的载荷及截面尺寸如图所示.许用拉应力[σl ]=40MPa ,许用压应力[σc ]=160MPa .解:(1) 画梁的弯矩图(2) 盘算截面几何性质42.572.522264157.542.53020021520030100157.5 30200200303020060.12510i CiC i zCAA y y mmAIy dA y dy y dy m --⨯⨯+⨯⨯===⨯+⨯==⨯⨯+⨯⨯=⨯∑∑⎰⎰⎰(3) 强度盘算B 截面的最大压应力3max620100.157552.4 []60.12510B C C C zC M y MPa I σσ-⨯⨯===⨯B 截面的最大拉应力3max6(0.23)2010(0.230.1575)24.12 []60.12510B C t t zC M y MPa I σσ--⨯-===⨯C 截面的最大拉应力3max610100.157526.2 []60.12510C C t t zC M y MPa I σσ-⨯⨯===⨯梁的强度足够.(4) 评论辩论:当梁的截面倒置时,梁内的最大拉应力产生在B 截面上.3max620100.157552.4 []60.12510B C t t ZC M y MPa I σσ-⨯⨯===⨯梁的强度不够.6.19. 试盘算图示工字形截面梁内的最大正应力和最大剪应力. xmax max 15 20 Q kN M kNm==(2) 查表得截面几何性质3*max14113.8 6z z I W cm cm b mmS ===(3) 盘算应力最大剪应力*3max max max151018.10.0060.138Z Z Q S MPabI τ⨯===⨯最大正应力3max max62010141.814110M MPa W σ-⨯===⨯6.22. 起重机下的梁由两根工字钢构成,起重机自重Q=50kN ,起重量P=10kN .许用应力[σ]=160MPa ,[τ]=100MPa .若暂不斟酌梁的自重,试按正应力强度前提选定工字钢型号,然后再按剪应力强度前提进行校核.解:(1)(2) (3) C 截面:B()(506)()501204.17C C M x x x dM x x dxx m =-=-==此时C 和D 截面的弯矩是104.25 134.05C D M kNm M kNm==D 截面:()(106)(8)()381203.17D D M x x x dM x x dxx m =+-=-==此时C 和D 截面的弯矩是98.27 140.07C D M kNm M kNm==最大弯矩值是max 140.07 M kNm=(4) 按最大正应力强度前提设计查表取25b *max1021.3z z I b mm cmS==(5) 按剪应力强度校核当起重机行进到最右边时(x =8m ),梁内剪应力最大; x剪应力强度盘算*3max maxmax581013.6[]220.010.213zzQ SMPabIττ⨯===⨯⨯剪应力强度足够.6.23. 由三根木条胶合而成的悬臂梁截面尺寸如图所示,跨度l=1 m.若胶合面上的许用切应力为0.34 MPa,木材的许用曲折正应力为[σ[τ]=1 MPa,试求允许载荷P解:(1)max maxQ P M Pl==(2) 梁曲折正应力强度前提maxmax2262[]16[]10100.10.153.75661M PlW bhbhP kNlσσσ==≤⨯⨯⨯≤==⨯(3) 梁曲折切应力强度前提maxmax633[]222[]21100.10.151033Q PA bhbhP kNτττ==≤⨯⨯⨯⨯≤==(4)胶合面上切应力强度前提2222max1336312222[]244212[]0.34100.10.153.8250.15660.02544zQ h P hy ybhIbhP kNhyτττ⎛⎫⎛⎫=-=-≤⎪ ⎪⎝⎭⎝⎭⨯⨯⨯⨯≤==⎛⎫⎛⎫--⎪ ⎪⎝⎭⎝⎭允许载荷:[P]=3.75 kN.6.27.在图中,梁的总长度为l ,受均布载荷q 感化.若支座可对称地向中点移动,试问移动距离为若干时,最为合理? 解:(1) 束缚反力2B C ql R R ==(2) 截面上的最大正弯矩和最大负弯矩22,max 2,max228822ql l ql ql qla M a qa M +-⎛⎫=--=- ⎪⎝⎭=-(3) 二者数值相等时最为合理2222822440410.20782ql qla qa a la l l a l l-=+-=-+-+===。
第6章弯曲应力教学目的:在本章的学习中要求熟练掌握梁纯弯曲时横截面上正应力计算公式的推导过程,理解推导过程中所作的假设。
掌握中性层、中性轴等基本概念和含义。
弯曲正应力和剪应力强度条件的建立和相应的计算。
理解横力弯曲正应力计算仍用纯弯曲公式的条件和近似程度。
从弯曲强度条件出发,掌握提高弯曲强度的若干措施。
教学重点:纯弯曲梁横截面上正应力公式的分析推导;横力弯曲横截面上正应力的计算,最大拉应力和最大压应力的计算;弯曲的强度计算;弯曲横截面上的剪应力。
教学难点:弯曲正应力、剪应力推导过程和结果以及弯曲中心的概念。
教具:多媒体。
教学方法:采用启发式教学,通过提问,引导学生思考,让学生回答问题。
教学内容:梁纯弯曲和横力弯曲时横截面上的正应力;梁横力弯曲时横截面上的切应力;提高弯曲强度的若干措施。
教学学时:6学时。
教学提纲:6.1 梁的纯弯曲1、几个基本概念(1)平面弯曲和弯曲中心变形后梁轴线的位移方向沿着加载方向的弯曲情况,称为平面弯曲。
怎样加载才能产生平面弯曲?若梁的横截面有对称平面时,载荷必须作用在对称平面内,才能发生平面弯曲。
若梁的横截面没有对称平面时,载荷的作用线必须通过截面的弯曲中心。
什么叫弯曲中心?当载荷的作用线通过横截面上某一点特定点时,杆件只产生弯曲而无扭转。
这样的特定点称为弯曲中心。
关于弯曲中心位置的确定及工程上常见图形的弯曲中心位置。
①具有两个对称轴或反对称的截面,如工字形、圆形、圆环形、空心矩形截面等,弯曲中心与形心(两对称轴的交点)重合,如图(a),(b),(c)所示。
②具有一个对称轴的截面,如槽形和T形截面,弯曲中心必在对称轴上,如图(d)、(e)所示。
③如果截面是由中线相交于一点的几个狭长矩形所组成,如L形或T形截面,则此交点就是弯曲中心,如图(e)、(f)所示。
④不对称实心截面的弯曲中心靠近形心。
这种截面在荷载作用线通过形心时也将引起扭转,但由于这种截面的抗扭刚度很大,弯曲中心与形心又非常靠近,故通常不考虑它的扭转影响。