更高更妙的物理-竞赛课件2：点击静力学问题解答技巧

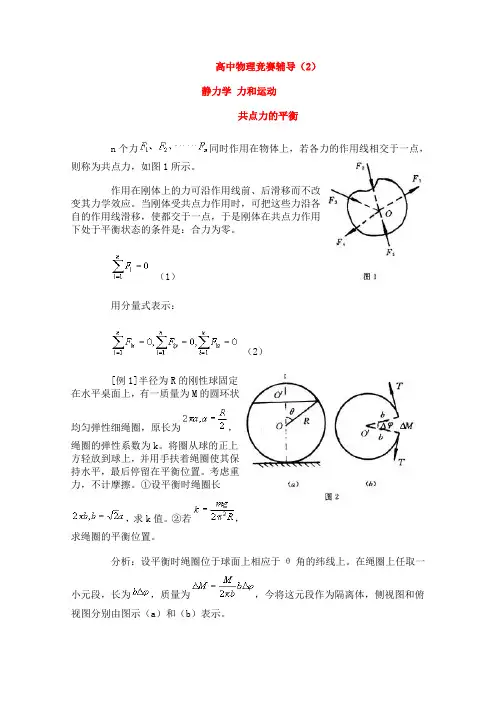
高中物理竞赛辅导（2）静力学力和运动共点力的平衡n个力同时作用在物体上，若各力的作用线相交于一点，则称为共点力，如图1所示。

作用在刚体上的力可沿作用线前、后滑移而不改变其力学效应。

当刚体受共点力作用时，可把这些力沿各自的作用线滑移，使都交于一点，于是刚体在共点力作用下处于平衡状态的条件是：合力为零。

（1）用分量式表示：（2）[例1]半径为R的刚性球固定在水平桌面上，有一质量为M的圆环状均匀弹性细绳圈，原长为，绳圈的弹性系数为k。

将圈从球的正上方轻放到球上，并用手扶着绳圈使其保持水平，最后停留在平衡位置。

考虑重力，不计摩擦。

①设平衡时绳圈长，求k值。

②若，求绳圈的平衡位置。

分析：设平衡时绳圈位于球面上相应于θ角的纬线上。

在绳圈上任取一小元段，长为，质量为，今将这元段作为隔离体，侧视图和俯视图分别由图示（a）和（b）表示。

元段受到三个力作用：重力方向竖直向下；球面的支力N方向沿半径R指向球外；两端张力，张力的合力为位于绳圈平面内，指向绳圈中心。

这三个力都在经线所在平面内，如图示（c）所示。

将它们沿经线的切向和法向分解，则切向力决定绳圈沿球面的运动。

解：（1）由力图（c）知：合张力沿经线切向分力为：重力沿径线切向分力为：（2-2）当绳圈在球面上平衡时，即切向合力为零。

（2-3）由以上三式得（2-4）式中由题设：。

把这些数据代入（2-4）式得。

于是。

（2）若时，C=2，而。

此时（2-4）式变成tgθ=2sinθ-1,即 sinθ+cosθ=sin2θ,平方后得。

在的范围内，上式无解，即此时在球面上不存在平衡位置。

这时由于k值太小，绳圈在重力作用下，套过球体落在桌面上。

[例2]四个相同的球静止在光滑的球形碗内，它们的中心同在一水平面内，今以另一相同的球放以四球之上。

若碗的半径大于球的半径k倍时，则四球将互相分离。

试求k值。

分析：设每个球的质量为m，半径为r ，下面四个球的相互作用力为N，如图示（a）所示。

高中物理竞赛辅导讲义静力学高中物理竞赛辅导讲义第1篇静力学【知识梳理】一、力和力矩1．力与力系（1）力：物体间的的相互作用（2）力系：作用在物体上的一群力①共点力系②平行力系③力偶2．重力和重心（1）重力：地球对物体的引力（物体各部分所受引力的合力）（2）重心：重力的等效作用点（在地面附近重心与质心重合）3．力矩（1）力的作用线：力的方向所在的直线（2）力臂：转动轴到力的作用线的距离（3）力矩①大小：力矩=力×力臂，M =FL②方向：右手螺旋法则确定。

右手握住转动轴，四指指向转动方向，母指指向就是力矩的方向。

③矢量表达形式：M r F =? （矢量的叉乘），||||||sin M r F θ=? 。

4．力偶矩（1）力偶：一对大小相等、方向相反但不共线的力。

（2）力偶臂：两力作用线间的距离。

（3）力偶矩：力和力偶臂的乘积。

二、物体平衡条件1．共点力系作用下物体平衡条件：合外力为零。

（1）直角坐标下的分量表示ΣF ix = 0，ΣF iy = 0，ΣF iz = 0（2）矢量表示各个力矢量首尾相接必形成封闭折线。

（3）三力平衡特性①三力必共面、共点；②三个力矢量构成封闭三角形。

2．有固定转动轴物体的平衡条件：3．一般物体的平衡条件：（1）合外力为零。

（2）合力矩为零。

4．摩擦角及其应用（1）摩擦力①滑动摩擦力：f k = μk N（μk－动摩擦因数）②静摩擦力：f s ≤μs N（μs－静摩擦因数）③滑动摩擦力方向：与相对运动方向相反（2）摩擦角：正压力与正压力和摩擦力的合力之间夹角。

①滑动摩擦角：tanθk=μ②最大静摩擦角：tanθsm=μ③静摩擦角：θs≤θsm（3）自锁现象三、平衡的种类1．稳定平衡：当物体稍稍偏离平衡位置时，有一个力或力矩使之回到平衡位置，这样的平衡叫稳定平衡。

2．不稳定平衡：当物体稍稍偏离平衡位置时，有一个力或力矩使它的偏离继续增大，这样的平衡叫不稳定平衡。

3．随遇平衡：当物体稍稍偏离平衡位置时，它所受的力或力矩不发生变化，它能在新的位置上再次平衡，这样的平衡叫随遇平衡。

第二部分：静力学一、复习基础知识点一、 考点内容1．力是物体间的相互作用，是物体发生形变和物体运动状态变化的原因。

2．重力是物体在地球表面附近所受到的地球对它的引力，重心。

3．形变与弹力，胡克定律。

4．静摩擦，最大静摩擦力。

5．滑动摩擦，滑动摩擦定律。

6．力是矢量，力的合成与分解。

7．平衡，共点力作用下物体的平衡。

二、 知识结构⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎩⎨⎧→→→⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎭⎫ ⎝⎛--→⎪⎪⎭⎫ ⎝⎛→→⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫ ⎝⎛→⎪⎪⎭⎫ ⎝⎛-→的灵活使用方法：整体法和隔离法产生条件、摩擦力、弹力、重力顺序原则受力分析实效原则图解法（几何法）力的分解式法图解法（几何法）、公力的合成力的等效性使物体产生形变物体产生加速度）改变物体运动状态（使力的效果效果各异作用力与反作用力效果相同平衡力支持力等回复力、浮力、压力、动力、阻力：向心力、效果子力、电场力、磁场力不接触的力：重力、分产生条件、大小、方向力接触的力：弹力、摩擦性质力的种类物体受力物体同时定是施力物体施力物体同时定是受力相互性受力物体施力物体物体间作用物质性力的属性—物体间的相互作用—力的定义力.......321 三、 复习思路在复习力的概念时,同学们应注重回顾学过的各种具体的力,包括电磁学中的各种力,也可以联系牛顿第三定律展开研究力的相互性。

对于重力,在复习时可以联系万有引力定律,分清为什么“重力是由于地球的吸引而产生的力”。

且通过分析物体随地球自转需向心力,最终认识重力与万有引力之间的差异很小,一般可认为2地R GMmmg =。

摩擦力是本单元的重点,也是难点，要结合具体的例子，对摩擦力的大小和方向，摩擦力的有无的讨论以及物体在水平面、斜面上、竖直墙上等的滑动摩擦力与弹力的关系等，要分门别类地进行讨论、研究。

高中物理静力学问题的解题技巧静力学是物理学中的一个重要分支，研究物体在静止状态下的力学性质。

在高中物理学习中，静力学问题是一个常见的考点，也是学生容易遇到困惑的地方。

本文将从不同角度出发，介绍一些解决静力学问题的技巧和方法，帮助高中学生更好地应对这类题目。

一、平衡条件的应用在解决静力学问题时，平衡条件是一个基本的概念。

平衡条件包括力的平衡和力矩的平衡。

力的平衡是指物体所受的合外力为零，力矩的平衡是指物体所受的合外力矩为零。

通过应用平衡条件，可以解决一些简单的静力学问题。

例如，考虑一个悬挂在天花板上的吊灯，我们需要确定吊灯所受的张力大小。

首先，我们可以将吊灯看作一个物体，受到重力的作用。

根据力的平衡条件，吊灯所受的张力必须等于重力的大小。

而对于力矩的平衡条件，我们可以选择合适的点作为旋转中心，使得吊灯所受的力矩为零。

通过这两个平衡条件，我们可以求解出吊灯所受的张力。

二、利用图像分析问题在解决静力学问题时，画出合理的图像是非常有帮助的。

通过图像，我们可以更直观地理解问题，并且可以利用几何关系解决问题。

例如，考虑一个斜面上放置的物体，我们需要求解物体所受的支持力和摩擦力。

首先，我们可以画出斜面的示意图，标明物体所受的各个力。

接下来，我们可以利用几何关系，如正弦定理、余弦定理等，将问题转化为几何问题。

通过解几何问题，我们可以求解出支持力和摩擦力的大小。

三、应用力的分解在解决静力学问题时，应用力的分解是一个常用的方法。

通过将力分解为平行和垂直于某个方向的分力，可以简化问题的分析和求解。

例如，考虑一个斜面上放置的物体，我们需要求解物体所受的支持力和摩擦力。

我们可以将重力分解为平行和垂直于斜面的分力，然后利用力的平衡条件解决问题。

通过这种方法，我们可以将原问题转化为两个简单的问题，进而求解出支持力和摩擦力的大小。

四、利用静摩擦力与滑动摩擦力的关系在解决静力学问题时，静摩擦力与滑动摩擦力之间存在一定的关系。

当外力小于或等于静摩擦力时，物体处于静止状态；当外力大于静摩擦力时，物体开始滑动。

处理静力学平衡问题技法三巧巧取研究对象巧解汇交力系巧用矢量图解F 1F 2F矢量求和图解法则12=+F F F 矢量求差图解法则12=-F F F F 1F 2F 相加矢量首尾相接，和从第一个加数“尾”指向最后一个加数“头”相减两矢量箭尾共点，差连接两箭头，方向指向“被减数”A CB O D EF如图所示，三角形ABC 三边中点分别为D 、E 、F ，在三角形中任取一点O ，如果、、三个矢量代表三个力，那么这三个力的合力为A. B. C. D. OAOB OC DO OE OF DOO A GR θmgθL+Δl R F N F T cos 2L l R θ+∆=由几何关系知由力△与几何△相似得k l G L l R ⋅∆=+∆G L k G l R ∆=-()cos 2kRL R kR G θ=-()1cos 2kL kR G θ-=-如图所示，一个重为G 的小环，套在竖直放置的半径为R 的光滑大圆环上．有一劲度系数为k ，自然长度为L (L ＜2R )的轻弹簧，其上端固定在大圆环的最高点A ，下端与小环相连，不考虑一切摩擦，则小环静止时弹簧与竖直方向的夹角θ为多大？θmmgF 约tan -1μF max F 约F min tan -1μ()1max tan tan -=+F mg θμ()1min tan tan -=-F mg θμsin cos sin cos cos sin cos sin -+≤≤+-F θμθθμθθμθθμθ如图所示，倾角为θ的斜面与水平面保持静止,斜面上有一重为G 的物体A 与斜面间的动摩擦因数为μ,且μ<tan θ,现给A 施以一水平力F ,设最大静摩擦力与滑动摩擦力相等,求水平推力F 多大时物体能地斜面上静止？静摩擦力达到最大时,斜面约束力作用线方向与斜面法线成摩擦角!θθF 1F 2F 1F 2F 2FF sec 22F θcot F θ将力F 分解为F 1和F 2两个分力，若已知F 的大小及F 1和F 2的夹角θ，且θ为钝角，则当F 1、F 2大小相等时，它们的大小为;当F 1有最大值时，F 2大小为.2θπθ-专题2-问题1F 1如图所示，放在水平面上的质量为m 的物体，在水平恒力F 1作用下，刚好做匀速直线运动．若再给物体加一个恒力，且使F 1＝F 2（指大小），要使物体仍按原方向做匀速直线运动，力F 2应沿什么方向？此时地面对物体的作用力大小如何？专题2-问题2G F tan -1μ水平恒力与重力、地面约束力作用而平衡时,三力构成闭合三角形：F F +=-211地1μμμF F +=+211地2μμμF 2F 2加F 2仍构成闭合三角形：如图所示，一光滑三角支架，顶角为θ=45°，在AB 和AC 两光滑杆上分别套有铜环，两铜环间有细线相连，释放两环，当两环平衡时，细线与杆AB 夹角60°，试求两环质量比M/m ．系统处于平衡时,两环所受绳拉力沿绳且等值反向,支架施支持力垂直各杆,以此为依据作每环三力平衡矢量图:B A mgMg F T F T 对环M sin 30sin 22T F Mg πθ=⎛⎫- ⎪⎝⎭ 60 15 θ对环M θ/230θ/2sin15sin 22T F mg πθ=⎛⎫- ⎪⎝⎭ sin 30sin15M m = 622+=如图所示，用细绳拴住两个质量为m 1、m 2（m 1＜m 2）的质点，放在表面光滑的圆柱面上，圆柱的轴是水平的，绳长为圆柱横截面周长的1/4．若绳的质量及摩擦均不计，系统静止时，m 1处细绳与水平夹角α是多少？系统处于平衡时,两质点所受绳拉力沿绳切向且等值, 圆柱施支持力垂直柱面,以此为依据作每质点三力平衡矢量图:αO m 1m 2m 1gm 2gαα对质点11sinTF m g α=对质点22cos T F m g α=21sin tan cos m m ααα==121tanm m α-=F TF T如图所示，两个质量相等而粗糙程度不同的物体m 1和m 2，分别固定在一细棒的两端，放在一倾角为α的斜面上，设m 1和m 2与斜面的摩擦因数为μ1和μ2，并满足tanα= ，细棒的质量不计，与斜面不接触，试求两物体同时有最大静摩擦力时棒与斜面上最大倾斜线AB 的夹角θ．12μμsin mg α系统处于平衡时,两物体所受轻杆力等值反向,沿斜面上每物体受下滑力、最大静摩擦力及杆作用力，每物体三力平衡矢量关系如图:AB m1m 2θαF 1cos mg μαsin mg α2cos mg μα分别以a 、b 、c 表示各力：cbac ϕθ在力矢量三角形中运用余弦定理：()22224cos b c a ca ϕ=+-222co 4s 4c a bcaϕ+-=()()2222444sin ac c a b caϕ-+-=在力矢量三角形中运用余弦定理：222sin 2cos sin a a c ac ϕϕθ⎛⎫=+- ⎪⎝⎭22222sin sin 2cos a a c ac ϕθϕ=+-()()2222222182a b c a c c -=-+-()()222222cos 82a b cac cθ-=+-代入题给数据：1212s 2o 2c μμθμμ+=+尽量取整体需“化内为外”时取部分方程数不足时取部分整、分结合，方便解题取两环一线为研究对象F N 2mgF fF2NF mg=f F F=取下环为研究对象mgFF T F T一个直角支架AOB ，AO 水平放置，表面粗糙，OB 竖直，表面光滑，AO 上套有小环P ，OB 上套有小环Q ，两环质量均为m ，两环间由一不可伸长的轻绳相连，并在某一位置平衡，如图所示．现将P 向左移一小段距离，两环再次达到平衡，那么移动后的平衡状态与原来相比，AO 杆对P 环的支持力F N 、摩擦力F f 及细绳上的拉力F T 的变化情况是A. F N 不变，F f 变大，F T 变大B.F N 不变，F f 变小，F T 变小C. F N 变大，F f 不变，F T 变大D.F N 变大，F f 变小，F T 变大P Q O ABF312取2、3两环为研究对象，3环重力设为GTT3GT G=取2环为研究对象θ2G 2cos 3GT θ=2cos 3θ=θhr 由几何关系得tan r hθ=00co 25t 5r r h θ==三根不可伸长的相同细绳，一端系在半径为r 0的环1上，彼此间距相等．绳穿过半径为r 0的第3个圆环，另一端用同样方式系在半径为2r 0的圆环2上，如图所示．环1固定在水平面上，整个系统处于平衡．试求第2个环中心与第3个环中心之距离（三个环用同种金属丝制作，摩擦不计）T一个底面粗糙质量为Ｍ的劈放在粗糙的水平面上，劈的斜面光滑且与水平面成30°夹角，用一端固定的轻绳系一质量为m 的小球，轻绳与斜面的夹角为30°,如图所示．当劈静止时，求绳中拉力的大小；若地面对劈的最大静摩擦力等于地面对劈的支持力的k 倍，为使整个系统静止，求k 的最小值30°专题2-问题3取小球为研究对象求绳中拉力:30°30302cos 303T mg F mg ==T F T F 取整体为研究对象求地面k 值(M +m )gΦ=tan -1k tan -1kT F F 地()()sin sin 30 TM m gF ϕϕ+=+()()sin 303sin M m m ϕϕ++=()2313M m m k+=+363m k M m =+如图所示，一长L 、质量均匀为M 的链条套在一表面光滑，顶角为α的圆锥上，当链条在圆锥面上静止时，链条中的张力是多少？专题2-问题4链条的受力具有旋转对称性．链条各部分间的张力属于内力,需将内力转化为外力，我们可以在链条中隔离出任一微元作为研究对象，链条其它部分对微元的拉力就成为外力，对微元根据平衡规律求解:F TF T F i αnπ∆θ=2当∆∆∆→,sin 22θθθi T T F F F ∆∆==⋅2sin 222θθ链条微元处于平衡△mgF NiF iT F mg ∆⋅=∆2cot22θα2αT n M F g n =⋅cot22απMg =cot 22απ压延机由两轮构成，两轮直径各为d ＝50cm ，轮间的间隙为a ＝0.5 cm ，两轮按反方向转动，如图2-15上箭头所示．已知烧红的铁板与铸铁轮之间的摩擦系数μ＝0.1．问能压延的铁板厚度b 是多少？ab分析铁板受力如图：F NF fθθ铁板能前进，应满足cos sin N N F F μθθ≥分析几何关系求角θ：22d b a --2dθ22222tan 22d d b a d b a θ-⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭=--解得b ≤0.75 cmμ≤,其各部分所受力的作用线延长后必汇交于一点,其合力为零.m 1m 2O6030 (m 1+m 2)g取两球一杆为研究对象，分析受力研究对象处于静止，所受三力矢量构成闭合三角形!N 1N 230由力矢量三角形即得21tan 3013N N ==1231N N :=:如图所示，一个半球形的碗放在桌面上，碗口水平，O 是球心，碗的内表面光滑．一根轻质杆的两端固定有两个小球，质量分别是m 1、m 2，当它们静止时，m 1、m 2与球心的连线跟水平面分别成60°30°角，则碗对两小球的弹力大小之比是A. 1∶2 B. ∶1 C. 1∶ D.∶2333CAB6030D解:FABBC 球系统为一“三力杆”！60⑴由三力平衡关系图得2cos60CD GF G ==2sin603AB F G G==⑵由几何关系图得F AB60细线BC 与竖直成60°角如图所示，BC 两个小球均重G ,用细线悬挂而静止于A 、G 两点，细线BC 伸直.求:⑴AB 和CD 两根细线的拉力各多大？⑵细线BC 与竖直方向的夹角是多大？如图所示，光滑半球壳直径为a ，与一光滑竖直墙面相切，一根均匀直棒AB 与水平成60°角靠墙静止，求棒长．专题2-问题5棒AB 受三力:ABOGF AF B棒AB 处于静止,三力作用线汇交于一点!30θ在三角形BCD 中由正弦定理:C()L L ⋅=-sin 6022sin sin 30θθ-=13tan6θ又aL a ⋅-=sin 302sin /2θL a =-1L a -=3139aL =+131313如图所示，在墙角处有一根质量为m 的均匀绳，一端悬于天花板上的A 点，另一端悬于竖直墙壁上的B 点，平衡后最低点为C ，测得绳长AC=2CB ，且在B 点附近的切线与竖直成α角，则绳在最低点C 处的张力和在A 处的张力各多大？专题2-问题6AαC取BC 段绳为研究对象:αmg/3最低点C 处的张力F TC 为F T CF Btan 3TCmg F α=取AC 段绳为研究对象:F T CF A2mg/32mg/3tan 3mgα222tan 33A mg mg F α⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭24tan 3mg α+=如图所示，有一轻杆AO 竖直放在粗糙的水平地面上，A 端用细绳系住，细绳另一端固定于地面上B 点，已知θ=30°，若在AO 杆中点施一大小为F 的水平力，使杆处于静止状态，这时地面O 端的作用力大小为________，方向________ 。

第2讲 静力学复习本讲提示：受力分析是高中物理中一项重要的基本功，包含常见力的性质，平衡力的规律两大基本内容。

本讲我们从常见模型一点点的入手，逐步巩固的复习。

复习模块一：常见模型的特征力 知识点睛1.弹力的性质以及规律弹力是由于形变长生的力，具体的体现在弹簧，接触面，杆，绳等。

弹簧弹力：胡克定律F kx =．轻绳：弹力方向沿绳且指向绳收缩方向轻杆：与轻绳不同，轻杆的弹力可以指向任意方向 面和面：弹力垂直于接触面 球和球：弹力沿两球球心连线难点：轻杆的弹力，可以自由转动的轻杆只有两个受力点时，弹力一定沿杆方向，可以是拉力也可以是压力。

对于多个点受力的轻杆，必须用力矩平衡与力平衡规律联立分析。

2.判断弹力有无：①消除法：去掉与研究对象接触的物体，看研究对象能否保持原状态，若能则说明此处弹力不存在，若不能则说明弹力存在．如图：球A 静止在平面B 和平面C 之间，若小心去掉B ，球静止，说明平面B 对球A 无弹力，若小心去掉C ，球将运动，说明平面C 对球有支持力．②假设法：假设接触处存在弹力，做出受力图，再根据平衡条件判断是否存在弹力．如图，若平面B 和平面C 对球的弹力都存在，那么球在水平方向上将不再平衡，故平面B 的弹力不存在，平面C 的弹力存在．③替换法：用轻绳替换装置中的轻杆，看能否维持原来的力学状态，如果可以，则杆提供的是拉力，如果不能，则提供支持力．3.判断摩擦物体间有相对运动或相对运动的趋势．有相对运动时产生的摩擦力叫滑动摩擦力，有相对运动趋势时产生的摩擦力叫静摩擦力．①滑动摩擦力：N F F μ=，μ是动摩擦因数，与接触物体的材料和接触面的粗糙程度有关，与接触面的大小无关．N F 表示压力大小，可见，在μ一定时，N F F ∝．②静摩擦力：其大小与引起相对运动趋势的外力有关，根据平衡条件或牛顿运动定律求出大小．静摩擦力的大小在零和最大静摩擦力max F 之间，即max 0F F ≤≤．静摩擦力的大小与N F 无关，最大静摩擦力的大小与N F 有关．③方向：滑动摩擦力方向与相对运动方向相反，静摩擦力方向与相对运动趋势方向相反． 判断静摩擦力的有无：在接触面粗糙，两物体接触且互相挤压的条件下，可使用下列方法假设法：假设没有静摩擦力，看物体是否发生相对运动，若发生，则存在相对运动趋势，存在静摩擦力．反推法：根据物体的状态和受力分析推出静摩擦力的大小和方向．4.摩擦角与自锁当物体与支持面之间粗糙，一旦存在相对运动趋势，就会受静摩擦力作用，设最大静摩擦因数为μ（中学不要求最大静摩擦因数跟动摩擦因数的区别），则最大静摩擦力为f M＝μF N 。