实验三 连续和离散系统的复频域分析
- 格式:doc
- 大小:329.58 KB
- 文档页数:13

实验三 连续信号的频域分析1.实验目的:(1)掌握周期信号分解和合成的方法。
(2)掌握非周期信号频谱分析方法。
2.实验原理(1)周期信号的分析与合成周期为T 的周期信号的傅里叶级数有三角型与指数型两种形式,分别表示为:()()()000011cos sin cos n n n n n n f t a a n t b n t A n t ωωωφ∞∞===++=+∑∑和()0j n t n n f t F eω∞=-∞=∑ 式子中,各系数的计算公式和相互关系如下:()/20/21T T a f t dt T -=⎰,()()/2/200/2/222cos ,sin ,T T n n T T a f t n tdt b f t n tdt T T ωω--==⎰⎰ ()0/2/21T jn t n T F f t e dt T ω--=⎰,arctan n n n n b A a φ⎛⎫==- ⎪⎝⎭傅里叶级数表明周期信号可以分解为正弦信号或虚指数的线性组合。
由三角型的系数可画出周期信号的单边幅度谱和相位谱,由指数型的系数可画出周期信号的双边谱,它们都是离散谱。
上述系数可以用MA TLAB 函数quad 或quadl 计算。
它们的调用格式为:y = quad(FUN,A,B), 和 y = quadl(FUN,A,B)其中,FUN 是被积函数名或函数句柄;A 和B 分别是积分区间的下限和上限。
比如,系数n a 可以如下计算:()2*,/2,/2/n a quad FUN T T T =-,(T 为信号周期)PS: quad:采用递推自适应的Simpson 法来计算,在低精度的非光滑曲线计算中是最有效的;quad1:采用递推自适应的Lobatto 法来计算,在高精度的光滑曲线计算中更为高效; 例1 求周期为4,幅度为1、脉冲宽度为2的对称矩形脉冲信号的三角型傅里叶级数。
参考:T = 4;A = 1;tao = 2;w0 = 2*pi/T;N = 6;f = @(n) (2*quad (@(t)(A*rectpuls(t,tao).*cos(n*w0*t)),-T/2,T/2)/T); %@(n):匿名函数,自定义matlab 中的函数,表示随后跟随的是属于变量n 的函数。

实验三:连续和离散系统的复频域分析一:实验原理1.掌握连续时间函数的拉普拉斯正变换及反变换 2.掌握离散时间函数的Z 变换和Z 反变换 3. 掌握连续系统复频域分析 4 掌握离散系统复频域分析二:实验原理1 拉氏变换的正变换和逆变换(1)定义:信号f(t)进行拉普拉斯变换及反变换的公式如下⎰∞∞--=dt e t f s F st)()( ⎰∞+∞-=j j st ds e s F j t f σσπ)(21)( 其中F(s)可以表示为有理分式)()()(s A s B s F =或零极点相乘1212()()()()()()()m n s z s z s z F s k s p s p s p ---=---形式A(s)和B(s)都是s 的多项式,m z z ,1是F(s)的零点,n p p ,1是F(s)的极点,k 为F(s)的增益。
(2)拉氏变换的函数调用正变换: Fs = laplace(f); 逆变换 f = ilaplace(Fs)2 Z 变换的正变换和逆变换(1)定义:正变换: 0()()n n F z f n z ∞-==∑ 反变换:11()()2n cf n F z z dz jπ-=⎰其中F(z)可以表示为有理分式)()()(z A z B z F =或零极点相乘1212()()()()()()()m n z z z z z z F z k z p z p z p ---=---形式 A(z)和B(z)都是z 的多项式,m z z ,1是F(z)的零点,n p p ,1是F(z)的极点,k 为F(z)的增益。
(2) Z 变换的函数调用正变换: F = ztrans(f) )()(z F F n f f =⇒= 逆变换 f = iztrans (F) )()(n f f z F F =⇒=三:实验内容1 拉普拉斯正变换和逆变换(1)分别求1)(=t f ,()(2)f t tu t =-,())(1)(t u e t f at--=的拉氏变换,写出拉氏变化结果 %% f(t)=tu(t-2)syms f t Fsf=t*heaviside(t-2); Fs = laplace(f); simplify(Fs)%% 信号f(t)=1-exp(-at)的拉氏变换syms Fs f a t f = 1-exp(-a*t); Fs = laplace(f); Fs=simplify(Fs)%% 直流信号1的拉氏变换f = sym(1); % creates a symbolic expression for 1 Fs = laplace(f) Fs=simplify(Fs)(2)分别求)3)(1()5)(2(10)(++++=s s s s s s F ,2()56s e F s s s -=++的反变换)(t f%% 求F(S)=10(s+2)(s+5)/s(s+1)(s+3)的拉氏反变换f(t)syms Fs f sFs =10*(s+2)*(s+5)/(s*(s+1)*(s+3)); f = ilaplace(Fs); Fs=simplify(Fs)%% F(s)=2*exp(-s)/(s^2+5s+6)syms Fs f sFs=exp(-s)/(s^2+5*s+6); f = ilaplace(Fs); Fs=simplify(Fs)2 离散信号的Z 域正变换和逆变换(1) 分别求)()()(n u a n f n =, 1)(=n f ,()2(1)3(2)f n n n δδ=-+-,1()(1)n f n a u n =---的Z 变换,并标清清楚ROC %% 信号f(t)=a^n 的Z 变换syms Fz f n a=1/3;f = a^n;Fz = ztrans(f); simplify(Fz)%% 直流信号1的Z 变换f = sym(1); % creates a symbolic expression for 1 Fz = ztrans(f) %% ()2(1)3(2)f n n n δδ=-+-的Z 变换Syms f n FzF=2*dirac(n-1)+3*dirac(n-2); Fz = ztrans(f); simplify(Fz)(2)分别求5.05.1)(22+-=z z z z X (1>z )和)2(23)(22>+-=Z z z z z X 时Z 反变换()x n %% 求F(z)=z^2/(z^2-1.5z+0.5)的Z 反变换f(n)syms Fz f zFz=z^2/(z^2-1.5*z+0.5); f = iztrans(Fz); simplify(Fz)%% 求F(z)=z^2/(z^2-3z+2)的Z 反变换f(n)Fz=z^2/(z^2-3*z+2); f = iztrans(Fz); simplify(Fz)3 连续系统和离散系统的系统函数(1)将微分方程转化为系统函数)(s H (或)(jw H ),并求冲激响应)(t h 和阶跃响应)(t gdtt de t r dt t dr dt t r d )()(6)(5)(22=++零初始状态⇔65)()()(2++==s s ss E s R s H %% 阶跃响应和冲激响应syms Hs Ht t s Hs=s/(s^2+5*s+6); Ht=ilaplace(Hs); Gt=int(Ht,t,0,t) Ht=simplify(Ht) Gt=simplify(Gt)subplot(211);ezplot(Ht) subplot(212);ezplot(Gt)同理求:)(2)()(3)(4)(22t e dt t de t r dt t dr dtt r d +=++零初始状态⇔342)()()(2+++==s s s s E s R s H (2) 差分方程和系统函数)(z H 之间的转换(2)3(1)2()(1)y n y n y n x n +-++=+零初始状态⇔23)()()(2+-==z z z z X z Y z H %% 离散系统 y(n+2)-3y(n+1)+2y(n)=x(n+1) 阶跃响应和冲激响应syms Hz Hn n z Gn Hz=z/(z^2-3*z+2); Hn=iztrans (Hz); Gn=int(Hn,n,0,n) Hn=simplify(Hn) Gn=simplify(Gn)subplot(211);ezplot(Hn) subplot(212);ezplot(Gn)同理求下列差分方程的h(t)和g(t))2()(6)1(5)2(+=++-+n x n y n y n y 零初始状态⇔65)()()(22+-==z z z z X z Y z H )()(2)1(n x n y n y =++零初始状态⇔21)()()(+==z z X z Y z H )(2)(n u n x n = ()0.9(1)0.1(2)0.05()y n y n y n x n --+-=零初始状态⇔211.09.0105.0)()()(--+-==zz z X z Y z H 3 零输入响应、零状态响应和全响应在MA TLAB 中,已知差分方程的系数,输入,初始条件,调用filter()函数解差分方程.调用filter()函数的格式为:y=filtier(b,a,x,xic),参数x 为输入向量(序列),b,a 分别为差分方程系数,xic 是等效初始状态输入数组(序列).确定等效初始状态输入数组xic(n),可使用Signal Processing toolbox 中的filtic()函数,调用格式为:y=filtic(b,a,y,x) .其中y=[y(-1),y(-2),…,y(-N)],x=[x(-1),x(-2),…,x(-M)] .(1)已知差分方程)()(2)1(3)2(n x n y n y n y =++++ ,式中 x(n)=)(2.0n u n,y(0)=2 ,y(1)=1 ,分别求零状态响应,零输入响应和全响应y ,分析该系统的稳定性。


信息科学与工程学院《信号与系统》实验报告四专业班级电信 09-班姓名学号实验时间 2011 年月日指导教师陈华丽成绩实验名称离散信号的频域分析实验目的1. 掌握离散信号谱分析的方法:序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换,进一步理解这些变换之间的关系;2. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab实现;3. 熟悉FFT算法原理和FFT子程序的应用。
4. 学习用FFT对连续信号和离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
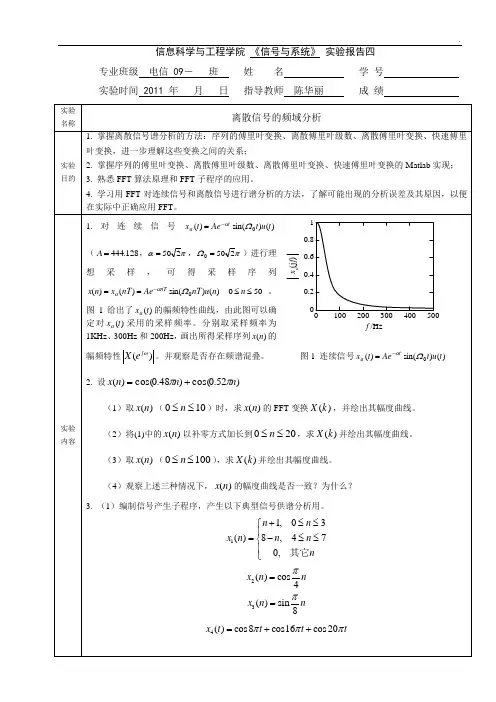
实验内容1.对连续信号)()sin()(0tutAetx taΩα-=(128.444=A,πα250=,πΩ250=)进行理想采样,可得采样序列50)()sin()()(0≤≤==-nnunTAenTxnx nTaΩα。
图1给出了)(txa的幅频特性曲线,由此图可以确定对)(txa采用的采样频率。
分别取采样频率为1KHz、300Hz和200Hz,画出所得采样序列)(nx的幅频特性)(ωj eX。
并观察是否存在频谱混叠。
图1 连续信号)()sin()(0tutAetx taΩα-=2. 设)52.0cos()48.0cos()(nnnxππ+=(1)取)(nx(100≤≤n)时,求)(nx的FFT变换)(kX,并绘出其幅度曲线。
(2)将(1)中的)(nx以补零方式加长到200≤≤n,求)(kX并绘出其幅度曲线。
(3)取)(nx(1000≤≤n),求)(kX并绘出其幅度曲线。
(4)观察上述三种情况下,)(nx的幅度曲线是否一致?为什么?3. (1)编制信号产生子程序,产生以下典型信号供谱分析用。
11,03()8,470,n nx n n nn+≤≤⎧⎪=-≤≤⎨⎪⎩其它2()cos4x n nπ=3()sin8x n nπ=4()cos8cos16cos20x t t t tπππ=++10.80.60.40.20100200300400500xa(jf)f /Hz(2)对信号1()x n ,2()x n ,3()x n 进行两次谱分析,FFT 的变换区间N 分别取8和16,观察两次的结果是否一致?为什么?(3)连续信号4()x n 的采样频率64s f Hz =,16,32,64N =。

实验三 连续信号、系统的频域分析、复频域分析一、实验目的1、理解频域分析的MA TLAB 实现方法。
2、求解系统的频率响应。
3、理解函数的拉氏变换,并进行复频域 二、实验时数: 2学时三、实验相关知识:(一)连续信号的频谱分析 1、周期信号的傅里叶级数计算设周期信号x(t)的基本周期为T 1,且满足狄里克利条件,则其指数形式的傅里叶级数系数Fn 为:1112211()T jn tn T F f t ed t T ω--=⎰其中n 为-∞,∞之间的整数;角频率ω1=2π/T 1。
因为计算机不能计算无穷多个系数,所以我们假设需要计算的谐波次数为N ,则总的系数个数为2N+1个。
在确定了信号的周期T 1和时间步长dt 之后,对某一个系数,上述系数的积分公式可以近似为:[]111111121211112111()()()()()/kMMT jn t jn tn k T k Tjn t jn t jn t M F f t ed t f t ed tT T f t f t f t eeed t T ωωωωω---=---==⎡⎤=⋅⋅⎣⎦∑⎰对于全部需要的2N+1个系数,上面的计算可以按照矩阵运算实现。
需要强调的是,时间变量的变化步长dt 的大小对傅里叶级数系数的计算精度的影响非常大,dt 越小,精度越高,但是,计算机计算所花的时间越长。
例3-1:求如图所示方波信号的幅度谱,并画出频谱图。
(A=1,τ=0.5,T 1=2)MATLAB 实现傅里叶级数计算的程序如下: dt = 0.01;T1 = 2;w1 = 2*pi/T1; t = -T1/2:dt:T1/2; tau = 0.5; A = 1;f = A*(u(t + tau/2) - u(t - tau/2)); subplot(2,1,1) plot(t,f)axis([-T1/2, T1/2, -0.1, 1.1]) title('f(t)时域波形') N = 10; n = -N:N;Fn = f*exp(-j*t'*w1*n)*dt/T1; subplot(2,1,2) stem(n,Fn) hold on dw = 0.01;w = -N*w1:dw:N*w1;F = A*tau/T1 * sinc(w*tau/2/pi); plot(w/w1,F,'--')title('傅里叶级数F_n')2、周期信号的合成以及Gibbs 现象从傅里叶级数的合成式(Synthesis equation )1()jn tn n f t F eω∞=-∞=∑可以看出,用无穷多个不同频率和不同振幅的周期复指数信号可以合成一个周期信号。

实验三离散信号与系统的连续频域分析一、实验目的1.离散时间信号的DTFT的MA TLAB实现;2.进行离散时间系统的DTFT分析;3.理解系统函数和频率相应之间的关系。
二、实验内容1.自定义一个长度为8点的信号,信号幅度值也由自己任意指定,对该信号作DTFT,分别画出幅度谱和相位谱;2.已知离散时间系统差分方程为y(n)-0.5y(n-1)+0.06y(n-2)=x(n)+x(n-1),求出并画出其频率响应;3.求该系统系统函数,并画极零点图,并通过freqz函数求频率响应。
三、实验平台MATLAB集成系统(MA TLAB6.5版本以上)四、设计流程查找离散时间系统信号的幅度和相位函数→通过MATLAB帮助阅读函数的使用→编写程序→在MATLAB上调试→书写实验报告。
五、程序清单参考程序附后。
六、要求1.通过参考程序进行仿真,并理解程序;2.对重要语句进行解释,附在程序行后面;3.理解函数的含义及参数所表示的意义。
本实验中如freqz函数、abs函数和angle函数。
参考程序:1n=0:7;x=(0.9*exp(j*pi/3)).^n; w=-pi:pi/200:pi;X=x*(exp(-j*pi/4)).^(n'*w); magX=abs(X);angX=angle(X);subplot(2,1,1);plot(w/pi,magX);xlabel('w/pi');ylabel('幅度|X|'); subplot(2,1,2);plot(w/pi,angX);xlabel('w/pi');ylabel('相位(rad/π)');-1-0.8-0.6-0.4-0.200.20.40.60.810246w/pi幅度|X |-1-0.8-0.6-0.4-0.200.20.40.60.81-2-1012w/pi相位(r a d /π)2a=[1,-0.5,0.06];b=[1,1,0];m=0:length(b)-1;l=0:length(a)-1; w=0:pi/500:pi;num=b*exp(-j*m'*w); den=a*exp(-j*l'*w); H=num./den;magH=abs(H);angH=angle(H); H1=freqz(b,a,w);magH1=abs(H1);angH1=angle(H1);subplot(2,2,2);plot(w/pi,angH/pi);grid; xlabel('w (frequency in pi units)');ylabel('相位(rad/π)');subplot(2,2,1);plot(w/pi,magH);grid;xlabel('w (frequency in pi units)');ylabel('幅度|H|'); subplot(2,2,3);plot(w/pi,magH1);grid;xlabel('w (frequency in pi units)');ylabel('幅度|H1|'); subplot(2,2,4);plot(w/pi,angH1/pi);grid; xlabel('w (frequency in pi units)');ylabel('相位(rad/π)');axis([0,1,-0.8,0]);figure(2);zplane(b,a);0.51w (frequency in pi units)相位(r a d /π)0.51w (frequency in pi units)幅度|H |0.51w (frequency in pi units)幅度|H 1|0.51w (frequency in pi units)相位(r a d /π)-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.81Real PartI m a g i n a r y P a r t。

实验四连续时间信号与系统的频域分析一、实验目的掌握连续时间信号的傅里叶变换及傅里叶逆变换的实现方法,掌握连续时间系统的频域分析方法,熟悉MATLAB 相应函数的调用格式和作用,掌握使用MATLAB 来分析连续时间信号与系统的频域特性及绘制信号频谱图的方法。
二、实验原理(一)连续时间信号与系统的频域分析原理1、连续时间信号的额频域分析 连续时间信号的傅里叶变换为:()()dt e t f j F t j ωω-∞∞-⎰=傅里叶逆变换为:()()ωωπωd e j F t f t j ⎰∞∞-=21()ωj F 称为频谱密度函数,简称频谱。
一般是复函数,可记为:()()()ωϕωωj e j F j F =()ωj F 反映信号各频率分量的幅度随频率ω的变化情况,称为信号幅度频谱。
()ωϕ反映信号各频率分量的相位随频率ω的变化情况,称为信号相位频谱。
2、连续时间系统的频域分析 在n 阶系统情况下,数学模型为:()()()()()()()()t f b dtt df b dt t f d b dt t f d b t y a dtt dy a dt t y d a dt t y d a o m m n m m n o n n n n n n ++++=++++------11111111 令初始条件为零,两端取傅里叶变换,得:()()[]()()()[]()ωωωωωωωωj F b j b j b j b j Y a j a j a j a m n m n n n nn01110111++++=++++----表示为()()()()ωωωωj F j b j Y j a kmk kkn k k∑∑===0则 ()()()()()()()()()∑∑==----=++++++++==nk kk mk kk n n n n m m mm j a j b a j a j a j a b j b j b j b j F j Y j H 0001110111ωωωωωωωωωωω3、系统传递函数 系统传递函数定义为:()()()ωωωj H j Y j H =系统传递函数反映了系统内在的固有的特性,它取决于系统自身的结构及参数,与外部 激励无关,是描述系统特性的一个重要参数。


复频域分析实验报告复频域分析实验报告引言复频域分析是一种用于研究信号频谱特性的方法,它可以将信号分解为不同频率成分,并通过频谱图展示出来。
本实验旨在通过实际操作,探索复频域分析的原理和应用。
实验设备和方法本实验所使用的设备包括信号发生器、示波器和频谱分析仪。
首先,我们通过信号发生器产生一定频率和幅度的正弦信号,并将其连接到示波器上。
然后,通过示波器上的功能设置,将信号转换为频谱图,并使用频谱分析仪对其进行进一步的分析。
实验结果与分析在进行实验过程中,我们选择了不同频率和幅度的正弦信号进行测试。
通过观察频谱图,我们可以清晰地看到信号的频率成分和其对应的幅度。
例如,当输入一个频率为1kHz的正弦信号时,频谱图显示了一个明显的峰值,对应着信号的主要频率成分。
同时,我们还可以观察到其他频率成分的存在,这些成分可能是由于信号本身的非线性特性或干扰引起的。
在进一步的实验中,我们改变了信号的幅度,并观察了频谱图的变化。
结果表明,信号的幅度与频谱图中峰值的高度存在一定的关系。
当信号幅度增加时,对应的峰值也会随之增加,反之亦然。
这一结果说明了信号的幅度对频谱分析结果的影响。
除了正弦信号外,我们还测试了其他类型的信号,如方波和三角波。
通过对这些信号进行复频域分析,我们可以观察到它们的频谱特性与正弦信号有所不同。
例如,方波信号的频谱图显示了多个峰值,对应着方波的谐波成分。
而三角波信号的频谱图则呈现出连续的频率分布,没有明显的峰值。
这些结果说明了不同类型信号的频谱特性是不同的,复频域分析可以帮助我们深入了解信号的频谱结构。
实验应用与展望复频域分析在实际应用中有着广泛的用途。
例如,在音频处理领域,复频域分析可以用于音频信号的均衡器设计和音频效果的提取。
在通信领域,复频域分析可以用于调制解调器的设计和信号传输质量的评估。
此外,复频域分析还可以应用于图像处理、生物医学工程等领域。
然而,本实验只是对复频域分析的基本原理和应用进行了初步的探索。

实验三 离散时间系统的频域分析一、实验目的:加深对离散系统的频率响应分析和零、极点分布的概念理解。
二、实验内容理解离散系统的变换域分析原理,掌握常用matlab 程序。
三、实验仪器1、具有WINDOWS 98/2000/NT/XP 操作系统的计算机一台;2、MATLAB 编程软件。
四、实验原理:离散系统的时域方程为∑=N n 0d n y(k-n)= =∑=M n 0p n x (k -n )其变换域分析方法如下:频域 y (k )=x (k )*h (k ) =∑∞-∞=n x (n )h (k -n ) ⇔Y(Ω)= X(Ω) H(Ω)系统的频率响应为 H(Ω)= Ω-Ω-Ω-Ω-++++++=ΩΩjN N j jM M j e d e d d e p e p p D P ......)()(1010 Z 域y (k )=x (k )*h (k ) =∑∞-∞=n x (n )h (k -n ) ⇔Y(z )= X(z ) H(z )系统的转移函数为 H(z )=11101110......)()(----++++++=zd z d d z p z p p z D z P N M 在MATLAB 中,可以用函数[z ,p ,K]=tf2zp (num ,den )求得有理分式形式的系统转移函数的零、极点,用函数zplane (z ,p )绘出零、极点分布图;也可以用函数zplane (num ,den )直接绘出有理分式形式的系统转移函数的零、极点分图。
使h=freqz(num,den,w)函数可求系统的频率响应,w 是频率的计算点,如w=0:pi/255:pi, h 是复数,abs(h)为幅度响应,angle(h)为相位响应。
另外,在MATLAB 中,disp()就是屏幕输出函数。
五、实验步骤1求系统H(z )=45.02.02.01.012.03.03.01.013214321z z z z z z z z ++++-----------的零、的零、极点和幅度频率响应和相位响应。
实验三 连系统的时域及复频域分析一、实验目的1、熟悉LTI 连续时间系统的时域及复频域分析方法;2、熟悉系统的零输入响应、零状态响应及冲激响应的求解步骤;3、熟悉拉普拉斯变换的原理及性质,熟悉常见信号的拉氏变换。
3、学会用MA TLAB 进行部分分式展开,学会用MATLAB 进行Laplace 正、反变换。
4、学会用MA TLAB 分析LTI 系统的特性。
二、实验环境计算机,Matlab 软件三、实验原理(一)连续系统的时域分析LTI 连续时间系统以常系数微分方程描述,系统的零状态响应可通过求解初始状态为零的微分方程得到。
MATLAB 提供了专门用于求解零初始状态微分方程数值解的函数以及专门用于求连续系统冲激响应及阶跃响应并绘制其时域波形的函数,利用其可以方便的计算系统的响应。
1、连续时间系统零状态响应的求解LTI 连续时间以常系数微分方程描述,系统的零状态响应可通过求解初始状态为零的微分方程得到.在MATLAB 的控制系统工具箱提供了一个用于求解零初始状态微分方程数值解的函数lsim.其调用方式为: y=lsim(sys,f,t)式中,t 表示计算系统响应的抽样点向量;f 是系统输入信号向量;sys 是LTI 系统模型,用来表示微分方程、差分方程、状态方程。
在求解微分方程时,微分方程的LTI 系统模型sys 要借助tf 函数获得(Create transfer function model ),其调用方式为:sys=tf(b,a)式中,b 和a 分别为微分方程右端和左端各项的系数向量。
(注意:微分方程中为零的系数一定要写入向量a 和b 中。
)例1:系统的微分方程为:)()(100)('2)(''t x t y t y t y =++,已知输入信号)π2sin(10)(t t x =。
ts=0;te=5;dt=0.01;sys=tf([1],[1 2 100]);%注意系数与微分方程系数的对应关系t=ts:dt:te;f=10*sin(2*pi*t);y=lsim(sys,f,t); %LSIM Simulate time response of dynamic systems toarbitrary inputs. 注意调用格式。
连续时间信号与系统的频域分析实验报告(共9篇)信号与系统实验五__连续时间信号的频域分析实验名称:连续时间信号的频域分析报告人:姓名班级学号一、实验目的1、熟悉傅里叶变换的性质;2、熟悉常见信号的傅里叶变换;3、了解傅里叶变换的MATLAB实现方法。
二、实验内容及运行结果1、编程实现下列信号的幅度频谱:(1)求出f(t)=u(2t+1)-u(2t-1)的频谱函数F(w);请与f1(t) u(2t+1)-u(2t-1)的频谱函数F1(w)进行比较,说明两者的关系。
%(1)f(t)=u(2t+1)-u(2t-1)与f(t)=u(t+1)-u(t-1) syms t w t1 w1Gt=sym('Heaviside(2*t+1)-Heaviside(2*t-1)');Gt1=sym('Heaviside(t1+1)-Heaviside(t1-1)');Fw=fourier(Gt,t,w);Fw1=fourier(Gt1,t1,w1);FFw=maple('convert',Fw,'piecewise');FFw1=maple('convert',Fw1,'piecewise');FFP=abs(FFw);FFP1=abs(FFw1);subplot(2,1,1);ezplot(FFP,[-10*pi 10*pi]);axis([-10*pi 10*pi 0 1.5]);subplot(2,1,2);ezplot(FFP1,[-10*pi 10*pi]);grid;axis([-10*pi 10*pi 0 2.2]);不同点:F1(w)的图像在扩展,幅值是F(w)的两倍。
(2)三角脉冲f2(t)=1-|t|;|t|=1;ft=sym('(1+t)*Heaviside(t+1)-2*t*Heaviside(t)+(t-1)*Heaviside( t-1)');Fw=fourier(ft);subplot(211)ezplot(abs(Fw)); g2)');ft=ifourier(Fw,w,t)ft =exp(-4*t)*heaviside(t)-exp(4*t)*heaviside(-t)(2)F(w)=((i*w)+5*i*w-8)/((i*w)+6*i*w+5)syms t wFw=sym('((i*w)+5*i*w-8)/((i*w)+6*i*w+5)');ft=ifourier(Fw,w,t)ft =dirac(t)+(2*exp(-5*t)-3*exp(-t))*heaviside(t)三、讨论与总论通过本实验,掌握了信号的傅里叶变换的性质以及方法,对傅里叶变换的性质有进一步的提高。
一、实验目的1. 理解复频域分析的基本原理和概念。
2. 掌握利用拉普拉斯变换进行系统分析的方法。
3. 学习使用MATLAB进行复频域分析,包括拉普拉斯变换和逆变换的计算、系统函数的求解以及系统响应的绘制。
4. 理解系统稳定性、频率响应和时域响应之间的关系。
二、实验原理复频域分析是信号与系统分析中的一种重要方法,它通过拉普拉斯变换将时域信号和系统转换到复频域进行分析。
在复频域中,信号和系统的特性可以更直观地表示,便于分析和设计。
拉普拉斯变换是一种积分变换,它将时域信号f(t)转换为复频域信号F(s)。
其定义如下:\[ F(s) = \int_{0}^{\infty} f(t)e^{-st} dt \]其中,s是复数,称为复频率。
拉普拉斯逆变换将复频域信号F(s)转换为时域信号f(t)。
其定义如下:\[ f(t) = \mathcal{L}^{-1}\{F(s)\} = \frac{1}{2\pi j}\int_{\gamma -j\infty}^{\gamma + j\infty} F(s)e^{st} ds \]其中,γ是拉普拉斯变换的收敛带。
通过拉普拉斯变换,可以将线性时不变系统(LTI)的时域微分方程转换为复频域的代数方程,从而简化系统分析和设计。
三、实验内容及步骤1. 拉普拉斯变换和逆变换的计算使用MATLAB进行以下信号的拉普拉斯变换和逆变换计算:- 单位阶跃信号 u(t)- 单位冲激信号δ(t)- 指数信号 e^{-at}2. 系统函数的求解根据给定的系统微分方程,求解其系统函数H(s)。
3. 系统响应的绘制- 利用MATLAB绘制系统函数H(s)的幅度响应和相位响应。
- 利用MATLAB绘制系统对单位阶跃信号的响应和单位冲激信号的响应。
4. 系统稳定性分析- 根据系统函数H(s)的极点分布,判断系统的稳定性。
- 利用MATLAB绘制系统函数H(s)的零极点图,直观地观察系统稳定性。
5. 频率响应分析- 利用MATLAB绘制系统函数H(s)的频率响应,分析系统的带宽和截止频率。
信号与系统实验报告实验题目: 实验三:连续时间系统的复频域分析实验仪器: 计算机,MATLAB 软件101b s b a s a ++++++称为系统的特征多项式,征根,也称为系统的固有频率(或自然频率)。
为将个特征根,这些特征根称为()F s 极点。
根据求函数21()(1)F s s s =-的拉氏逆变换。
源代码:num = [1]; 结果为:r =-1 1 1 a=conv([1 -1],[1 -1]);den = conv([1 0], a); p =1 1 0 [r,p,k] = residue(num, den); k=03.示例3:求函数2224()(4)s F s s -=+的拉氏逆变换源代码:num = [1 0 -4];den = conv([1 0 4], [1 0 4]); [r,p,k] = residue(num, den);结果为:r =-0.0000-0.0000i 0.5000+0.0000i -0.0000+0.0000i 0.5000-0.0000ip =-0.0000+2.0000i -0.0000+2.0000i -0.0000-2.0000i -0.0000-2.0000i k=04.示例4:已知系统函数为:321()221H s s s s =+++,利用Matlab 画出该系统的零极点分布图,分析系统的稳定性,并求出该系统的单位冲激响应和幅频响应。
源代码: num=[1];den=[1 2 2 1]; sys=tf(num,den); poles=roots(den); figure(1);pzmap(sys);xlabel('Re(s)');ylabel(' Im(s)');title('zero-pole map'); t=0:0.02:10;h=impulse(num,den,t); figure(2);plot(t,h);xlabel('t(s)');ylabel('h(t)');title('Impulse Response'); [H,w]=freqs(num,den);figure(3);plot(w,abs(H));xlabel('\omega(rad/s)');ylabel('|H(j\omega)|');title('Magenitude Response'); 结果为:poles =-1.0000 -0.5000 + 0.8660i -0.5000 - 0.8660i (2) 已知象函数,试调用residue 函数完成部分分式分解,并写出逆变换。
一、实验目的1. 理解和掌握频域分析的基本原理和方法。
2. 熟悉MATLAB在频域分析中的应用。
3. 通过实验,深入理解线性系统在频域中的特性。
4. 培养分析和解决实际问题的能力。
二、实验原理频域分析是研究线性系统的一种重要方法,它将时域信号转换到频域进行分析,从而揭示系统在各个频率分量上的响应特性。
频域分析方法主要包括傅里叶变换、拉普拉斯变换、Z变换等。
1. 傅里叶变换:将时域信号转换到频域的数学方法,适用于连续时间信号。
其逆变换可以将频域信号转换回时域。
2. 拉普拉斯变换:将时域信号转换到复频域的数学方法,适用于连续时间信号。
其逆变换可以将复频域信号转换回时域。
3. Z变换:将时域信号转换到离散时间域的数学方法,适用于离散时间信号。
其逆变换可以将离散时间域信号转换回时域。
三、实验内容及步骤1. 实验一:连续时间信号的频域分析(1)利用MATLAB实现连续时间信号的傅里叶变换和逆变换。
(2)绘制信号的时域波形图、频谱图、相位图等。
(3)分析信号的频率成分、幅度、相位等特性。
2. 实验二:离散时间信号的频域分析(1)利用MATLAB实现离散时间信号的离散傅里叶变换(DFT)和离散傅里叶逆变换(IDFT)。
(2)绘制信号的时域波形图、频谱图、相位图等。
(3)分析信号的频率成分、幅度、相位等特性。
3. 实验三:线性系统的频域分析(1)利用MATLAB绘制系统的幅频特性曲线、相频特性曲线。
(2)分析系统的截止频率、带宽、稳定性等特性。
(3)比较不同系统的频域特性,分析其对信号处理的影响。
四、实验结果与分析1. 实验一:通过傅里叶变换,将时域信号转换到频域,可以直观地观察到信号的频率成分、幅度、相位等特性。
例如,对于正弦信号,其频谱图显示只有一个频率分量,且幅度和相位保持不变。
2. 实验二:离散傅里叶变换(DFT)是离散时间信号频域分析的重要工具。
通过DFT,可以将离散时间信号分解为多个频率分量,从而分析信号的频率特性。
实验3 离散时间系统的频域分析一、实验目的(1)了解DFS 、DFT 与DTFT 的联系;加深对FFT 基本理论的理解;掌握用MATLB 语言进行傅里叶变换时常用的子函数;(2)了解离散系统的零极点与系统因果性和稳定性的关系;加深对离散系统的频率响应特性基本概念的理解;熟悉MATLAB 中进行离散系统零极点分析的常用子函数;掌握离散系统幅频响应和相频响应的求解方法。
二、实验内容1. 已知离散时间系统函数为()432143213.07.05.11.112.01.03.01.02.0--------+-+-++++=zz z z z z z z z H 求该系统的零极点及零极点分布图,并判断系统的因果稳定性。
实验程序脚本文件:b=[0.2,0.1,0.3,0.1,0.2]; a=[1,-1.1,1.5,-0.7,0.3]; [z,p,k]=tf2zp(b,a); zplane(z,p)title('零极点分布图 ') 零极点图如下:因为系统函数的极点都在单位圆内部,所以该系统为因果稳定系统。
2. 已知离散时间系统的系统函数为()432143213.07.05.11.112.01.03.01.02.0--------+-+-++++=zz z z z z z z z H求该系统在π~0频率范围内的绝对幅频响应、相频响应。
实验程序脚本文件:b=[0.2 0.1 0.3 0.1 0.2]; a=[1 -1.1 1.5 -0.7 0.3]; [h,w]=freqz(b,a); subplot(2,1,1) plot(w,abs(h)); title('幅频响应'); subplot(2,1,2) plot(w,angle(h)) title('相频响应'); 运行以上程序可得:3. 已知()[]7,6,5,4,3,2,1,0=n x ,画出由离散时间傅里叶变换求得的幅度谱()()[]ωωj j e X e X a r g 和图形。
∞ 实验三 连续和离散系统的复频域分析一、实验目的1.掌握连续时间函数的拉普拉斯正变换及反变换;2.掌握离散时间函数的 Z 变换和 Z 反变换;;3.掌握连续系统复频域分析方法;4.掌握离散系统复频域分析方法。
二、实验仪器装有 MATLAB 软件的微型计算机 1 台三、实验原理3.1 拉氏变换的正变换和逆变换 (1)定义正变换: F (s ) = ⎰ f (t )e -st dt 反变换: f (t ) =1 ⎰σ + j ∞F (s )e st ds-∞2πjο - j ∞其中 F(s) 可以表示为有理分式 F (s ) =B (s )或零极点相乘形式A (s )F (s ) =k(s -z 1)(s -z 2)L (s -z m )(s - p 1)(s - p 2)L (s - p n )A(s)和 B(s)都是 s 的多项式,z 1,z 2,…,z m 是 F(s)的零点,p 1,p 2,…,p n 是 F(s)的极点, k 为 F(s)的增益。
(2)拉氏变换的函数调用正变换: Fs = laplace(f)逆变换:f = ilaplace(Fs)□⎰ 3.2 Z 变换的正变换和逆变换 (1)定义正变换: F (z) = ∑ f (n)z-nn =0反变换: f (n) =12π j cF (z)zn -1dz其中 F(z)可以表示为有理分式 F (z) = B(z)或零极点相乘形式A(z)F (z ) =k(z -z 1)(z -z 2)L (z -z m ) (z -p 1)(z -p 2)L (z -p n )A(z)和 B(z)都是 z 的多项式,z 1,z 2,…,z m 是 F(z)的零点,p 1,p 2,…,p n 是 F(z)的极点, k 为 F(z)的增益。
(2)Z 变换的函数调用正变换: F = ztrans(f)f = f (n ) ⇒ F = F (z )逆变换: f = iztrans (F) F = F (z ) ⇒ f = f (n )3.3 复频域分析其他相关函数(1) ezplot 函数调用格斯:ezplot(f)功能:符号型函数的绘图函数(2) dimpulse 函数调用格式:dimpulse(B,A[,N])功能:绘制传递函数 H(Z)的单位脉冲响应,其中 B ,A 分别是传递函数按 Z-1 的升幂排列的分子分母系数行向量,N 为指定的单位脉冲响应序列的点数。
(3) dstep 函数∞调用格式:dstep(B,A[,N])功能:绘制传递函数H(Z)的单位阶跃响应,其中B,A 分别是传递函数按Z-1 的升幂排列的分子分母系数行向量,N 为指定的单位脉冲响应序列的点数。
(4)lsim 函数调用格式:lsim(sys,x,t,zi)功能:计算系统在任意输入和零状态下的全响应。
sys 为状态空间形式的系统函数,zi 是系统的初始状态。
(5)filter 函数调用格式:y=filter(b,a,x,xic)功能:求解差分方程。
参数x 为输入向量(序列),b,a 分别为差分方程系数,xic 是等效初始状态输入数组(序列)。
确定等效初始状态输入数组xic(n),可使用filtic()函数。
调用格式为:y=filtic(b,a,y,x) 。
其中y=[y(-1),y(-2),…,y(-N)] ,x=[x(-1),x(-2),…,x(-M)]。
四、实验内容1、拉普拉斯正变换和逆变换(1)分别求f (t) =1,f (t) = tu(t - 2) ,f (t) =(1 - e-a t )u(t) 的拉氏变换;syms f t a FsFs=laplace(sym(1))syms f t Fsf=t*heaviside(t-2);Fs=laplace(f)syms f t Fs af=(1-exp(-a*t))*heaviside(t); Fs=laplace(f)syms f s FF=10*(s+2)*(s+5)/s*(s+1)*(s+3); f=ilaplace(F)syms f s FF=exp(-s)/(s^2+5*s+6);f=ilaplace(F)2、离散信号的Z 域正变换和逆变换(1)分别求f (n) = (a)n u(n) , f (n) =1 的Z变换;syms f z Fz n af=a^n*heaviside(n);Fz=ztrans(f)syms f z Fz n aFz=ztrans(sym(1))syms f z Fz n aFz=z^2/(z^2-1.5*z+0.5);f=iztrans(Fz)syms f z Fz n aFz=z^2/(z^2-3*z+2);f=iztrans(Fz)3、连续系统和离散系统的系统函数(1)将微分方程转化为系统函数H (s) ,并求冲激响应h(t) 和阶跃响应g(t)试求该系统的系统函数H (s) ,并求冲激响应h(t) 和阶跃响应g(t) 。
Fs=s/(s^2+5*s+6);syms f s FsFs=s/(s^2+5*s+6);f=ilaplace(Fs)、ezplot(f)syms f t k1f=int(3*exp(-3*t) - 2*exp(-2*t)); k1=int(f,t,0,t);ezplot(k1)(2)将方程转化为系统函数H (z) ,并求冲激响应h(z) 和阶跃响应g(z)已知系统的差分方程如下:y(n + 2) - 3y(n +1) + 2 y(n) = x(n +1)试求该系统的系统函数H (z) ,并求冲激响应h(z) 和阶跃响应g(z) 。
syms hz hn n z gnhz=z/(z^2-3*z+2);hn=iztrans(hz);gn=int(hn,n,0,n);simplify(hn)simplify(gn)subplot(211);ezplot(hn);subplot(212);ezplot(gn);4、连续系统和离散系统的零输入响应、零状态响应和全响应(1)已知连续系统的系统函数H (s) =R(s) =E(s) s s 2 + 5s + 6式中e(t) = 3u(t) ,y(0)=1,y'(0)=1;分别求该系统的零状态响应,零输入响应和全响应 y 。
%零输入响应a=[1 0];b=[1 5 6];sys=tf(a,b);%确定传递函数,一种新的表示方法t=0:0.01:3;sys1=ss(sys);%将传递函数模型转化为状态空间模型y=[1 1];u=zeros(1,length(t)); %自己建立一个1行的矩阵rzi=lsim(sys1,u,t,y); %求解零输入响应subplot(311);plot(t,rzi)%零状态响应syms s ff=ilaplace(3/((s+2)*(s+3)));%把分母分解因式t=0:0.01:3;rzs=3*exp(-2*t)-3*exp(-3*t);%已经将u(t)拉式变换过,整理出来的式子subplot(312);plot(t,rzs)%全响应R=rzi+rzs'; %必须要加“’”,要不然图像跟预期的不相符。
subplot(313);plot(t,R)19%零输入响应den=[1 3 2];num=[1];n1=0:5;count=length(n);y01=[2 1];x01=[0 0];x1=zeros(1,count);xzi=filtic(num,den,y01,x01) yzi=filter(num,den,x1,xzi)%零状态响应y02=[0 0];x02=[0 0];x2=(0.2).^n;xzs=filtic(num,den,y02,x02) yzi=filter(num,den,x2,xzs)%全响应y0=[2 1];x0=[0 0];x=(2).^n;xz=filtic(num,den,y0,x0)2021y=filter(num,den,五、心得体会1、这次我整体感觉是最难的,主要体现在第4题上,因为涉及到零输入响应和零状态响应的系统分析,加上差分方程等系统,还有自己对filtic 和filter 的参数调用不了解,在上网查阅资料看过其他的应用之后才把这求零状态和零输入响应的表示求出来。
2、对于第1、2题是最简单的拉普拉斯和Z 变换的函数应用很简单。
但是第三题自己遇到的第一个自己利用拉氏变换的微分性质把传函表示出来,第二个就是阶跃响应如何求,因为之前老师也说过就是对冲激响应在0-t 上积分,直接调用int 函数即可,自己比要求多做了一步画图,是为了更清楚地了解这个系统。
3、第四个首先遇到的是不知道怎么下手,而题目中给的那些函数有些不会调用,后面通过与同学讨论和查阅资料,知道了一些函数的使用方法,但还是有很多细节没考虑到,比如语句的调用sys=tf(a,b);%确定传递函数,一种新的表示方法sys1=ss(sys);%将传递函数模型转化为状态空间模型…………4、通过本次实验我感觉我的MATLAB编程能力还很欠缺,以及对系统的分析也不够透彻,之后我会多多练习分析系统方面的知识,并且能用MATLAB来实践。
22。