07.第7讲 牛顿法 DFP变尺度法
- 格式:ppt
- 大小:272.50 KB
- 文档页数:9

约束变尺度法Newton 法最突出的优点是收敛速度快,在这一点上其它算法无法比拟的。
因此,建议凡是Hesse 矩阵比较容易求出的问题,尽可能使用Newton 法求解。
但是,Newton 法也有一个严重缺陷,就是每次迭代都要计算目标函数的Hesse 矩阵和它的逆矩阵,当问题的维数较大时,计算量迅速增加,从而就抵消了Newton 法的优点。
为此,人们开始寻找一种算法既可以保持Newton 法收敛速度快的优点,又可以摆脱关于Hesse 矩阵的计算,这就是变尺度算法。
变尺度法是一种非常好的方法,其中DFP 算法和BFGS 算法。
可以说,直到目前为止,在不用Hesse 矩阵的方法中是最好的算法。
一、拟Newton 法为了吸收Newton 法收敛速度快的优点,同时避免Newton 法每次迭代都要计算目标函数的Hesse 矩阵和它的逆矩阵,人们提出了具有超线性收敛的拟Newton 法。
(一)拟Newton 法的基本原理在Newton 法中的基本迭代公式kk k k P t X X +=+1,其中1=k t ,)()]([12kkk Xf Xf P ∇∇-=-令)()(2kkkkXf gXf G∇=∇=,于是有,,,,21011=-=-+k g G X X k k k k其中X0是初始点, gk 和 Gk 分别是目标函数f (X )在点 Xk 的梯度和Hesse 矩阵.为了消除这个迭代公式中的Hesse 逆矩阵G-1k ,可用某种近似矩阵Hk=Hk(Xk)来替换它,即构造一矩阵序列{Hk}去逼近Hesse 逆矩阵序列{G-1k},此时kk k k g H X X -=+1事实上,式中 Pk= -Hk gk 无非是确定了第k 次迭代的搜索方向.为了取得更大的灵活性,考虑更一般的迭代公式kk k k k g H t X X -=+1其中步长tk 通过从Xk 出发沿Pk= -Hk gk 作直线搜索来确定.此式代表很广的一类迭代公式.例如,当Hk=I (单位矩阵)时,它变为最速下降法的迭代公式。

牛顿法牛顿法(英语:Newton's method)又称为牛顿-拉弗森方法(英语:Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。
方法使用函数的泰勒级数的前面几项来寻找方程的根。
起源:牛顿法最初由艾萨克·牛顿在《流数法》(Method of Fluxions,1671年完成,在牛顿去世后的1736年公开发表)中提出。
约瑟夫·鲍易也曾于1690年在Analysis Aequationum中提出此方法。
原理:二阶逼近牛顿法对局部凸函数找到极小值,对局部凹函数找到极大值,对局部不凸不凹函数可能找到鞍点牛顿法要求估计二阶导数。
牛顿法据称比直接计算要快了4 倍。
其中的两次迭代(第二步迭代被注释掉了)就是用的牛顿法来求解方程,也就是的根。
牛顿法的思想其实很简单,给定一个初始点,使用在该点处的切线来近似函数,然后寻找切线的根作为一次迭代。
比如对于这个例子,令,给定初始点,在该点处的导数是,由此可以得到该处的切线为,求解得到正是代码中的迭代。
当然代码的重点其实不在这里,而在0x5f3759df这个奇怪的magic number,用于得到一个好的初始点。
这个神奇的数字到底是谁发现的,根据wikipedia 上的说法似乎至今还没有定论。
xkcd 还为此画了一条漫画,讽刺说每次我们惊奇地发现工业界里不知道哪个无名人士写出了0x5f3759df之类的神奇数字,背后都有成千上万的其他无名人士我们无从知晓,说不定他们中的某一个人已经解决了P=NP 的问题,但是那人却还在调某个自动打蛋器的代码所以我们至今仍无知晓。
:D回到我们今天的话题,从这段代码中我们可以看到两点:牛顿法收敛非常快,对于精度要求不是特别高的情况,比如上面的图形学相关的计算中,甚至只用了一次计算迭代。
另一方面,初始值的选取非常重要,我们接下去将会看到,初始值选得不好有可能会直接导致算法不收敛。


牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行使用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
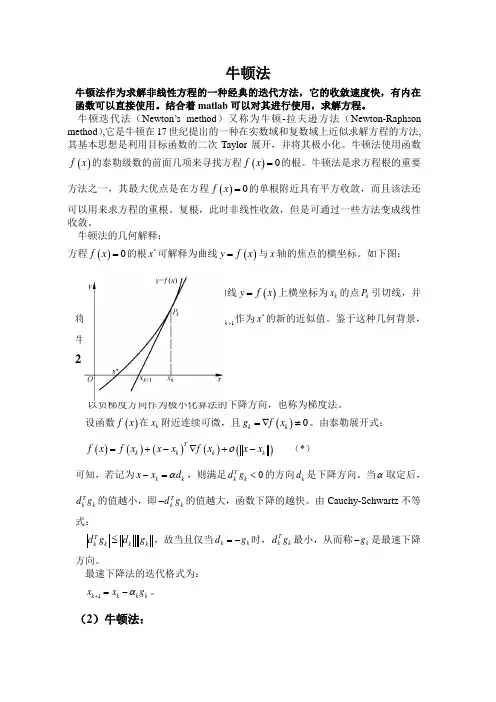
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()T k k k k fx f x x x f xx x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0T k k d g <的方向k d 是下降方向。
当α取定后,T k k d g 的值越小,即T k k d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:Tk k kk d g d g ≤,故当且仅当k k d g =-时,T k k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。



dfp算法原理
DFP算法,也称为DFP校正方法,是第一个拟牛顿法,由Davidon最早提出,后经Fletcher和Powell解释和改进,在命名时以三个人名字的首字母命名。
拟牛顿法多数时候均为对二阶导hessian矩阵或其逆矩阵的近似逼近,DFP所逼近的就是hessian逆矩阵。
其算法步骤如下:
假设已知目标函数及梯度,迭代轮数n,终止条件。
取初始点,精度;计算,若则停止,得到权重;否则转3;令,;令;求,令;计算,若则停止,得到权重;否则转7;计算;计算;令,转4。
求得的X即为每个特征的权重。
一般而言,针对公式会补充一个正定的充要条件:。
但是在实际实现中,本人发现很多时候,并不一定大于0,但距离0差距很小,一般在以内,因此可以将该约束进行放松。
以上内容仅供参考,如需更专业全面的信息,建议查阅数学或算法相关的专业书籍或咨询数学领域专家。


dfp变尺度法
DFP变尺度法(Davidon-Fletcher-Powell变尺度法)是一种拟牛顿优化算法,用于求解无约束极值问题它综合了梯度法和牛顿法的优点,具有较快的收敛速度和较广的应用范围DFP算法在优化领域中被认为是一种高效的方法,尤其在处理高维问题时具有显著优势。
DFP变尺度法的基本思想是在每次迭代中,用一组线性方程组来近似表示目标函数的Hessian矩阵这样,我们可以用较少的计算代价获得牛顿法类似的收敛速度变尺度法的关键在于选择合适的尺度矩阵,以保证算法的收敛性和稳定性。
DFP算法的步骤如下。
1.初始化:选择一个初始点x0.
2.计算目标函数的梯度g(x)。
f(x)=f(x0)+γ(x-x0).
其中,γ为尺度因子
3.计算Hessian矩阵的近似值H
H=I-γ²g²(x).
4.更新搜索方向。
s=-Hg(x).
5.更新x。
x=x0+αs.
其中,α为线搜索参数。
6.重复步骤2-5,直到满足终止条件(如收敛或达到迭代次数限制)。
DFP变尺度法在实际应用中通常与一维搜索技术和黄金分割法相结合,以提高收敛速度和稳定性此外,还可以根据问题特点对算法进行适当调整,如引入局部搜索、调整线搜索策略等,以适应不同问题的需求总之,DFP变尺度法是一种高效、实用的优化算法,在许多领域都得到了广泛应用。

牛顿法的完整流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!牛顿法的完整流程牛顿法是一种用于求解方程近似解的数值方法,它的流程简单清晰,非常适合在实际应用中进行求解。
一、变尺度法的基本思想变尺度法是在牛顿法的基础上发展起来的,它和梯度法亦有密切关系。
我们观察一下梯度法和阻尼牛顿法的迭代公式,即:式——(1)和——(2)分析比较这两种方法可知:梯度法的搜索方向为,只需计算函数的一阶偏导数,计算工作量小,当迭代点远离最优点时对突破函数的非二次性极为有利,函数值下降很快,但是当迭代点接近最优点时收敛速度很慢。
牛顿法的搜索方向为,不仅需要计算一阶偏导数而且要计算二阶偏导数矩阵及其逆矩阵.计算工作璧很大,但牛顿法具有二次收敛性,当迭代点接近最优点时收敛速度很快。
对这两种方法取其优,去其劣,迭代过程先用梯度法,后用牛顿法并避开牛顿法的赫森矩阵的逆矩阵的繁琐计算,这就是萌生建立“变尺度法”的基本构想。
下面对变尺度法的基本思想进行阐述。
变尺度法所构成的迭代公式为:——(3)式中为最优步长因子,由一维搜索而得;对照无约束优化迭代通式。
变尺度法的搜索方向应为;是根据需要人为构造的一个n×n阶对称矩阵,它在迭代过程中随迭代点的位置变化而变化。
若在初始点取为单位矩阵取I,则式(3}就成为式(1)表示的梯度法迭代公式,搜索方向为负梯度方向。
以后随着迭代过程不断地修正构造矩阵,使它在整个迭代过程中逐步地逼近目标函数在极小点处的赫森矩阵的逆矩阵。
当时。
式(3)就成为式(2)表示的阻尼牛顿法迭代公式。
这样,当迭代点逼近最优点时,搜索方向就趋于牛顿方向。
如能实现这种构想,那就综合了梯度法和牛顿法的优点,不直接计算,而是用变化的构造矩阵去逼近它,使算法更为有效。
构造矩阵在迭代过程中是变化的,称为变尺度矩阵。
由于变尺度法的迭代形式与牛倾法类似,不同的是在迭代公式中用来逼近,所以又称为“拟牛顿法”,变尺度法的搜索方向,最终要逼近牛顿方向,故又称为拟牛顿方向。
实现上述变尺度法的基本思想,关键在于如何产生这一合乎要求的变尺度矩阵,下面对此进行重点讨论。
二、构造变尺度矩阵的基本要求1.为了使拟牛顿搜索方向朝着目标函数值下降的方向,必须为对称正定矩阵。
牛顿法简介牛顿迭代法(Newton's method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
产生背景多数方程不存在求根公式,因此求精确根非常困难,甚至不可解,从而寻找方程的近似根就显得特别重要。
方法使用函数的泰勒级数的前面几项来寻找方程的根。
牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时线性收敛,但是可通过一些方法变成超线性收敛。
另外该方法广泛用于计算机编程中。
详细内容1、求解方程。
并不是所有的方程都有求根公式,或者求根公式很复杂,导致求解困难。
利用牛顿法,可以迭代求解。
原理是利用泰勒公式,在x0处展开,且展开到一阶,即f(x) = f(x0)+(x-x0)f'(x0)求解方程f(x)=0,即f(x0)+(x-x0)*f'(x0)=0,求解x = x1=x0-f(x0)/f'(x0),因为这是利用泰勒公式的一阶展开,f(x) = f(x0)+(x-x0)f'(x0)处并不是完全相等,而是近似相等,这里求得的x1并不能让f(x)=0,只能说f(x1)的值比f(x0)更接近f(x)=0,于是乎,迭代求解的想法就很自然了,可以进而推出x(n+1)=x(n)-f(x(n))/f'(x(n)),通过迭代,这个式子必然在f(x*)=0的时候收敛。
整个过程如下图:2、牛顿法用于最优化在最优化的问题中,线性最优化至少可以使用单纯行法求解,但对于非线性优化问题,牛顿法提供了一种求解的办法。
假设任务是优化一个目标函数f,求函数f的极大极小问题,可以转化为求解函数f的导数f'=0的问题,这样求可以把优化问题看成方程求解问题(f'=0)。
剩下的问题就和第一部分提到的牛顿法求解很相似了。
牛顿法牛顿法,又称牛顿拉夫森法,是牛顿在17世纪提出的一种近似求解实数和复数领域方程的方法。
大多数方程没有根公式,因此很难找到确切的根,甚至无法求解,因此找到方程的近似根非常重要。
方法使用泰勒函数级数的前几个项来查找方程的根。
牛顿迭代法是找到方程根的重要方法之一。
它的最大优点是它在方程的单根附近具有平方收敛,也可以用于找到方程的多根和复根。
此时,线性收敛是线性的,但是可以通过某些方法将其变为超线性收敛。
另外,该方法广泛用于计算机编程。
设是的根,选取作为的初始近似值,过点做曲线的切线,,则与轴交点的横坐标,称为的一次近似值。
过点做曲线的切线,并求该切线与x轴交点的横坐标,称为r的二次近似值。
重复以上过程,得的近似值序列,其中,称为的次近似值,上式称为牛顿迭代公式。
用牛顿迭代法解非线性方程,是把非线性方程线性化的一种近似方法。
把在点的某邻域内展开成泰勒级数,取其线性部分(即泰勒展开的前两项),并令其等于0,即,以此作为非线性方程的近似方程,若,则其解为,这样,得到牛顿迭代法的一个迭代关系式:。
已经证明,如果是连续的,并且待求的零点是孤立的,那么在零点周围存在一个区域,只要初始值位于这个邻近区域内,那么牛顿法必定收敛。
并且,如果不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。
迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法(或者称为一次解法),即一次性解决问题。
迭代算法是用计算机解决问题的一种基本方法。
它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
利用迭代算法解决问题,需要做好以下三个方面的工作:一、确定迭代变量在可以用迭代算法解决的问题中,至少存在一个可直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
§3.5 变尺度法DEF 变尺度法: 1. 变尺度的定义:每确定一次搜索方向,调整一次模(尺度)的大小,称为变尺度。
2. 基本思想:发扬梯度法和牛顿法各自的优点,避免两者各自的缺点,将两者结合起来,形成变尺度法。
3. 变尺度矩阵的构造:原则:使目标函数值有下降性,则变尺度矩阵应为实对称矩阵(请证明); 使算法有二次收敛性,则 S(k) (k=1,2,…)应关于 H(k) 是共轭的;构造变尺度矩阵的递推公式:4. 修正矩阵:了牛顿法的优点。
矩阵的逆矩阵,而利用及这样避免计算二阶导数即为牛顿法。
最终迭代时,时接近当不断修正尺度,逼近,中间的迭代即为梯度法,,首次迭代时,为拟牛顿方向。
的矩阵一个为变尺度矩阵,是:其中:迭代公式Hesse x f x H S x f x H S x H H x x x H H x f S I H x f H S n n H x f H x x k K k k K k K k k k k k k k k k k k k k k k ,)()]([,,)()]([,)]([*,)]([,)(,)(][,),(][)(1)()()(1)()(1)()()(1)()()()()0()()()()()()()()()1(∇-=∇-→→-∇==∇-=⨯∇-=----+α。
即:件)变尺度条件(拟牛顿条)()]()([,)()1()()1()1()()()1(k k k k k k k k x x x f x f Hx g H -=∇-∇∆=∆⋅∙++++次迭代时的修正矩阵。
为第其中:k E E H H k k k k )()()()1(,+=+5.步骤:(略)6. 方法评价:DEF 变尺度法以逐次逼近的方法实现 H-1 的计算,当目标函数的一阶导数易求时,以一阶代替二阶导数的计算是有效的方法。
算法的第一步是梯度法,最速下降;接近 x* 时,又采用二次收敛的共轭方向,总的收敛速度较快。