第二章插值法
- 格式:ppt
- 大小:782.00 KB
- 文档页数:47







第二章 插值法⏹ 多项式插值的存在性 ⏹ Lagrange 插值 ⏹ Newton 插值 ⏹ Hermit 插值 ⏹ 分段低次插值 ⏹ 三次样条插值在生产实践和科学研究所遇到的大量函数中,相当一部分是通过测量或实验得到的。
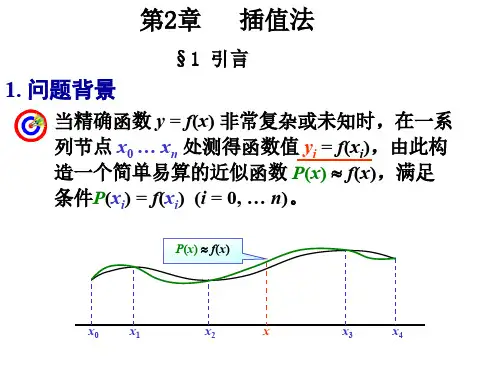
虽然其函数关系)(x f y =在某个区间[]b a ,是客观存在的,但是却不知道具体的解析表达式,只能通过观察、测量或实验得到函数在区间a ,b]上一些离散点上的函数值、导数值等,因此,希望对这样的函数用一个比较简单的函数表达式来近似地给出整体上的描述。
还有些函数,虽然有明确的解析表达式,但却过于复杂而不便于进行理论分析和数值计算,同样希望构造一个既能反映函数的特性又便于计算的简单函数,近似代替原来的函数。
插值法就是寻求近似函数的方法之一.在用插值法寻求近似函数的过程中,根据所讨论问题的特点,对简单函数的类型可有不同的选取,如多项式、有理式、三角函数等,其中多项式结构简单,并有良好的性质,便于数值计算和理论分析,因此被广泛采用。
本章主要介绍多项式插值、分段多项式插值和样条插值. 2.1 插值多项式的存在唯一性 2.1.1 插值问题设函数)(x f y =在区间],[b a 上有定义,且已知函数在区间],[b a 上n+1个互异点n x x x ,,,10 处的函数值)(i i x f y = i=0,1,…,n ,若存在一个简单函数)(x p y =,使其经过)(x f y =上的这n+1个已知点),(,),,(),,(1100n n y x y x y x (图5-1),即n i y x p i i ,,1,0 ,)( == (2.1.1)那么,函数)(x p 称为插值函数,点n x x x ,,,10 称为插值节点,],[b a 称为插值区间,求)(x p 的方法称为插值法,)(x f 称为被插函数。
若)(x p 是次数不超过n 的多项式,记为)(x p n ,即n n n x a x a a x p +++= 10)(则称)(x p n 为n 次插值多项式,相应的插值法称为多项式插值;若)(x p 为分段多项式,称为分段插值,多项式插值和分段插值称为代数插值。


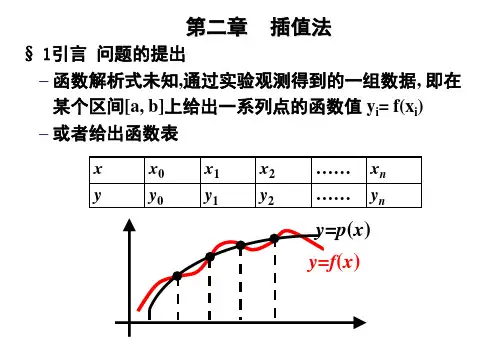
数值分析--第2章插值法第2章 插值法在科学研究与工程技术中,常常遇到这样的问题:由实验或测量得到一批离散样点,要求作出一条通过这些点的光滑曲线,以便满足设计要求或进行加工。
反映在数学上,即已知函数在一些点上的值,寻求它的分析表达式。
此外,一些函数虽有表达式,但因式子复杂,不易计算其值和进行理论分析,也需要构造一个简单函数来近似它。
解决这种问题的方法有两类:一类是给出函数)(x f 的一些样点,选定一个便于计算的函数)(x ϕ形式,如多项式、分式线性函数及三角多项式等,要求它通过已知样点,由此确定函数)(x ϕ作为)(x f 的近似,这就是插值法;另一类方法在选定近似函数的形式后,不要求近似函数过已知样点,只要求在某种意义下在这些样点上的总偏差最小。
这类方法称为曲线(数据)拟合法。
设已知函数f 在区间],[b a 上的1+n 个相异点ix 处的函数值(),0,,iif f x i n ==,要求构造一个简单函数()x ϕ作为函数()f x 的近似表达式()()f x x ϕ≈,使得()(),0,1,,iiix f x f i n ϕ=== (2-1) 这类问题称为插值问题。
称f 为被插值函数;()x ϕ为插值函数;nx x ,,0 为插值节点;(2-1)为插值条件。
若插值函数类{()}x ϕ是代数多项式,则相应的插值问题为代数插值。
若{()}x ϕ是三角多项式,则相应的插值问题称为三角插值。
若{()}x ϕ是有理分式,则相应的插值问题称为有理插值。
§1 Lagrange 插值1.1 Lagrange 插值多项式设函数f 在1+n 个相异点01,,,nx x x 上的值n i x f f ii ,,1,0),( ==是已知的,在次数不超过n 的多项式集合n P 中,求()nL x 使得(),0,1,,n i iL x f n n == (2-2) 定理2.1 存在惟一的多项式nn P L ∈满足插值条件(2-2)。