电压激励的压电层合悬臂梁横向振动分析_叶文强
- 格式:pdf
- 大小:312.25 KB
- 文档页数:6

实验十二 连续弹性体悬臂梁各阶固有频率及主振型测定一、一、实验目的1、 1、 用共振法确定连续弹性体悬臂梁的各阶固有频率和主振型。
2、 2、 观察分析梁振动的各阶主振型。
情况下,梁的振动是无穷多个主振型的迭加。
如果给梁施加一个合适大小的激扰力,且该力的频率正好等于梁的某阶固有频率,就会产生共振,对应于这一阶固有频率确定的振动形态叫做这一阶主振型,这时其它各阶振型的影响小得可以忽略不计。
用共振法确定梁的各阶固有频率及振型,我们只要连续调节激扰力,当梁出现某阶纯振型且振动幅值最大即产生共振时,就认为这时的激扰力频率是梁的这一阶固有频率。
实际上,我们关心的通常中最低几阶固有频率及主振型,本实验是用共振法来测定悬臂梁的一、二、l i β①根据《振动力学》,刘延柱,陈文良,陈立群著,1998版。
136页,例6.2-2式(g)A — A — 梁横截面积(m 2)l ρ—材料线密度(kg/m) l ρ=ρAρ—材料密度(kg/m 3) I —梁截面弯曲惯性矩(m 4)对矩形截面,弯曲惯性矩:123bhI = (m 4) (2)式中: b —梁横截面宽度(m) h —梁横截面高度(m) 本实验取l =( ) m b=( ) m h=( ) mE=20×1011Pa ρ=7800kg/m 3 各阶固有频率之比:f 1:f 2:f 3:f 4……=1:6.27:17.55 (3)理论计算可得悬臂梁的一、二、三阶固有频率的振型如图(3)所示:0.10.20.30.40.50.60.70.80.91-10120 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1-2020 0.10.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 10.511.5beam transvers vibration with one end clasped四、四、实验方法1、 1、 选距固定端L/4之处为激振点,将激振器端面对准悬臂梁上的激振点,保持初始间隙δ=6~8mm 。

悬臂梁式动力吸振器多频减振研究周荣亚【摘要】将悬臂梁作为动力吸振器附加在振动主结构上来达到振动抑制的目的,数值计算分析表明悬臂梁式动力吸振器具有多频减振特性.按照模态理论建立基于悬臂梁的具有集中参数的等效复式动力吸振器模型,悬臂梁的每一阶模态作为一个自由度的弹簧质量系统,把悬臂梁每阶模态的有效模态质量和等效模态刚度作为每一自由度弹簧质量系统的集中质量和刚度.用悬臂梁式动力吸振器的附加动刚度验证等效复式动力吸振器模型的正确性.将悬臂梁式动力吸振器附加在主梁末端,调谐悬臂梁式动力吸振器的前4阶模态达到对主悬臂梁的多频减振效果,证实了悬臂梁式动力吸振器多频减振特性.%Cantilever type dynamic vibration absorbers can be attached to the principal structure to suppress vibration effectively. Numerical analysis shows that the cantilever type absorbers have multi-band vibration reduction characteristics. In this paper, the equivalent multiple spring-mass oscillator system model of the cantilever type dynamic vibration absorber is established according to the modal superposition theory. Each mode of the cantilever type dynamic vibration absorber is treated as a single DOF spring-mass oscillator system. The effective modal mass and effective modal stiffness of each mode are treated as the lumped mass and stiffness of the equivalent multiple spring-mass oscillator system. The correctness of the multiple spring-mass oscillator system model is verified by dynamic stiffness test of the cantilever type absorber. Finally, the cantilever type dynamic vibration absorber is attached to the end of the principal beam, and the first 4modes of the absorber are found to reach the effect of multi-band vibration reduction.【期刊名称】《噪声与振动控制》【年(卷),期】2017(037)004【总页数】4页(P197-200)【关键词】振动与波;悬臂梁;复式动力吸振器;有效模态质量;多频减振【作者】周荣亚【作者单位】陕西铁路工程职业技术学院,陕西渭南 714000【正文语种】中文【中图分类】TB535.1振动是人们在生产生活中不可避免的现象,振动的存在使得工业生产设备产生疲劳破损,影响设备的精度,甚至缩短设备寿命。
179第七章 弹性连续体振动的准确解实际的振系都是弹性连续体系统,在很多情况下只是为了使问题简化,计算简便,才把它们简化成前几章所讨论的有限多的离散系统来分析。
当需要对弹性体振动问题作严密的分析时,这时就需要作为连续系统来处理。
弹性连续体问题与离散体问题有不同的特点,弹性连续体的质量、刚度、阻尼是连续分布的,因之具有无限多个自由度,需用无限多个点的独立坐标来表确定,其运动微分方程需要用偏微分方程来描述,而离散体在力学模型上具有明显的集中质量和不计质量的弹性元件,其自由度有限,运动以与自由度个数相等的二阶常系数微分方程来描述。
尽管如此,但两类问题在物理本质上是相同的,若把连续系统的质量分段聚集到有限个点上,各点之间用弹性元件连接起来便成为连续体,反之,离散系统当其质点数趋于无限多时就成为连续体,它们之间有相同的动力特性。
n 自由度连续体系统有n 个固有频率及主振型,而连续体则有无限多个固有频率及主振型,连续体中也存在各个主振型之间关于质量矩阵、刚度矩阵的正交性,对弹性体的响应分析,主振型迭加法有效。
本章将研究具有以下三个条件的理想弹性连续体振动问题的求解:1.材料是均匀的,具有各向同性;2.应力不超过弹性极限、并服从虎克定律;3.变形是微小的且是连续的。
具体是一维弹性体:轴、杆、梁等。
至于其它类弹性连续体如板、壳等的振动问题,因涉及到弹性力学知识,本章将不予讨论。
7-1弦的横向振动先研究最简单的弦的横向振动问题。
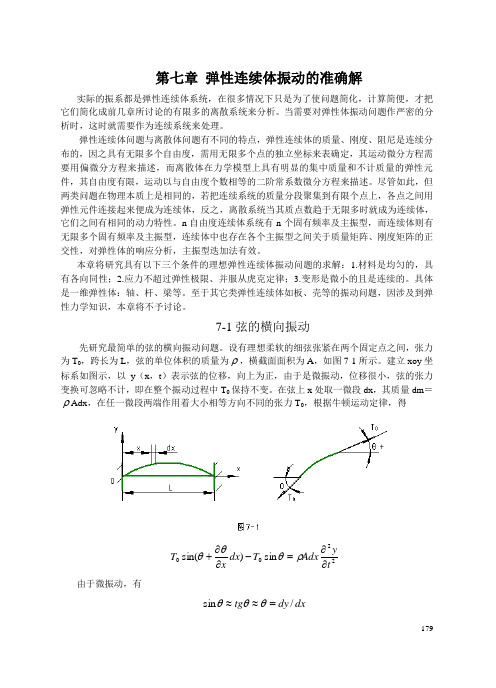
设有理想柔软的细弦张紧在两个固定点之间,张力为T 0,跨长为L ,弦的单位体积的质量为ρ,橫截面面积为A ,如图7-1所示。
建立xoy 坐标系如图示,以y (x ,t )表示弦的位移,向上为正,由于是微振动,位移很小,弦的张力变换可忽略不计,即在整个振动过程中T 0保持不变。
在弦上x 处取一微段dx ,其质量dm =ρAdx ,在任一微段两端作用着大小相等方向不同的张力T 0,根据牛顿运动定律,得2200sin )sin(tyAdx T dx x T ∂∂=-∂∂+ρθθθ由于微振动,有dx dy tg /sin =≈≈θθθ180故有2200)(ty Adx T dx x T ∂∂=-∂∂+ρθθθ代入x y∂∂=θ,简化后,即为 22220ty A x y T ∂∂=∂∂ρ 或写成22222t y a x y ∂∂=∂∂ (7-1) 式中AT a ρ0=称为波沿弦长度方向传播的速度。


基于在线识别与全维状态观测技术的埋入压电片复合梁的振动
主动控制研究
基于在线识别与全维状态观测技术的埋入压电片复合梁的振动主动控制研究
介绍利用埋入复合材料梁的压电传感器和驱动器对其振动进行主动控制的实验研究及其结果.利用埋入的压电传感器和驱动器对其进行模型识别而得出结构的动力学模型,再将该模型用于控制器的设计,其优点是当结构本身或者约束、环境等发生变化后,可对结构的模型重新进行在线识别,及时更新控制参数,避免控制失效,而且不需要事先知道结构的其他属性.应用最优控制理论的全维状态观测器技术,结合所选取的压电传感器和作动器识别的结构动力学模型,可以设计出其最优控制器.实验表明,传感器信号的频谱峰值最大可以被有效地降低20dB左右.
作者:吴克恭姜节胜 Janocha Hartmut 作者单位:吴克恭,姜节胜(西北工业大学,振动工程研究所,陕西,西安,710072)
Janocha Hartmut(德国萨尔大学,自动化过程实验室,萨尔州,德国,66123)
刊名:航空学报 ISTIC EI PKU英文刊名:ACTA AERONAUTICA ET ASTRONAUTICA SINICA 年,卷(期):2003 24(5) 分类号:O328 TB123 关键词:埋入压电材料复合梁振动主动控制在线识别全维状态观测器最优控制实验。

基于PolyMAX方法的悬臂梁振动模态分析作者:向玲鄢小安陈涛来源:《中国测试》2016年第04期摘要:为分析某悬臂梁的振动模态,根据锤击法模态测试流程,利用PolyMAX方法对悬臂梁的传递函数进行模态参数估计和识别。
利用有限元软件和欧拉梁理论仿真并计算该悬臂梁前五阶固有频率和振型。
结果表明:对悬臂梁的实验分析结果和理论值、仿真值吻合良好,说明锤击法的模态实验可靠,为以后分析相似结构的模态提供参考。
关键词:锤击法;悬臂梁;模态分析;振型文献标志码:A文章编号:1674-5124(2016)04-0132-040.引言模态分析是为识别系统的模态参数,为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据,在工程振动领域中有重要应用价值。
目前,Niels Saabve Ottosen等讨论了锤击法对地基板和梁进行模态分析中遇到的常见问题。
周云等在其基础上利用PloyMAX方法对弹性地基板进行了实验模态分析,为地基参数识别和损失诊断提供了手段。
刘军等利用自主开发的试验模态分析系统对某跑车车身进行了模态分析,对试验模态的改进具有推动作用。
根据文献可知利用Euler梁模型的固有特性可以在一定程度上模拟和反映汽轮机叶片的固有特性。
因此,研究悬臂梁结构的模态分析有重要意义。
鉴于此特殊功能的关系,本文利用锤击实验中的PloyMAX法对某悬臂梁进行了模态分析,为反映实验的准确性,用ANSYS软件仿真了悬臂梁模型,并利用传递矩阵法对悬臂梁进行了理论计算。
1.LMS b中PloyMAX振动模态分析1.1 LMS中的PloyMAX模态识别方法LMS公司最新推出LMS b中的PolvMAx模态识别方法,也称为多参考点最小二乘复频域法。
起初该方法只用来导出迭代法极大似然估计的最优初值,这种估计也称为公分母传递函数模型。
LSCF法超越其他参数估计技术最突出的优点是它可以得出非常清晰的稳态图,多参考法的主要好处是SVD这一步骤能避免分解留数,密集空间可以分离出来。