开关变换器的SSA建模
- 格式:doc
- 大小:654.50 KB
- 文档页数:18



同步开关输出噪声建模方法及仿真研究如今CMOS技术让一块FPGA器件可以拥有多个I/O接口。
同时,近几年,低功耗已开始成为高速I/O接口的主流概念。
降低功耗最有效的途径就是降低电压,而电压降低就会导致I/O接口所允许的噪声余量变小。
因此,对FPGA用户而言,量化芯片、封装和PCB环境下的系统级同步开关噪声(SSN)就显得十分必要。
本文对SSN进行了系统性介绍,着重介绍由FPGA输出缓冲导致的SSN。
这种噪声一般被称作同步开关输出噪声(SSO),与输入缓冲导致的SSN不同。
本文介绍了系统级SSO 的成因,并提出了一种分层的系统级SSO建模方法。
同时,本文还讲解了如何将SSO模型与频域和时域测量相关联,并给出了几种减小SSO的PCB设计方法。
系统级SSO的形成机制带FPGA的PCB是一个复杂的系统,可将其分为包含有源电路的芯片部分、带有嵌入式无源器件的支撑走线的封装部分,和为FPGA与外部提供连接的电路板部分。
在此类系统中,要想弄清芯片内部的噪声特性很困难。
因此,对与FPGA相连的PCB走线近端和远端的SSO进行量化就显得很有价值。
造成SSO的主要有两大因素:电源分配网(PDN)的阻抗和开关I/O之间的互感耦合。
从系统的角度来说,PDN中包含芯片级、封装级和板卡级的组件,这些组件共同为CMOS 电路供电。
当一定数量的CMOS输出驱动电路同时打开时,就会有很大电流瞬间涌入PDN 的感性电路元件中,从而产生一个delta-I压降。
互连结构产生寄生电感,例如球栅阵列封装上的电源焊球和PCB中的电源过孔。
这种快速变化的电流还会在电源/接地平面对之间激励起放射状的电磁波,电磁波从PCB的平面边缘反射回来,在电源/接地平面之间产生谐振,从而导致电压波动。
造成SSO的另一个重要原因是互感耦合,尤其是在芯片封装/PCB边沿周围产生的互感耦合。
芯片BGA封装上的焊球与PCB上的过孔都属于紧耦合的多导线结构。
每个I/O焊球及其相应的PCB过孔与离它最近的接地焊球和接地过孔构成一个闭合环路。


DC-DC开关变换器建模与数字仿真分析研究的开题报告一、研究背景随着电子技术的不断发展,直接得到的电源电压已经很难满足现代数码电子设备的需求。
同时,采用电池供电的便携式设备也更加普及。
因此,直流电源转换器(DC-DC变换器)被广泛应用于各种电子设备。
DC-DC变换器可将电池供电电压转换为适合电子设备使用的恒定电压、电流或功率等。
开关型DC-DC变换器通过开关原理实现高效率、小尺寸、轻重量的电源适配器。
同时,稳压、降噪等功能也是众多DC-DC 变换器需求的重要因素。
因此,对DC-DC开关变换器进行建模仿真是进行性能优化的首要步骤。
二、研究目的本研究旨在对DC-DC开关变换器进行建模与数字仿真分析,以评估系统性能和稳定性。
具体目标如下:1. 建立DC-DC开关变换器的电路模型,并设计合适的控制算法;2. 通过数字仿真分析,评估DC-DC开关变换器的性能指标,包括电压稳定性、纹波、效率等;3. 探索DC-DC开关变换器的优化方法,提高其效率和稳定性。
三、研究内容1. DC-DC开关变换器电路模型的建立通过建立电路模型,可以对DC-DC开关变换器进行数学分析。
本研究将使用模块化建模的方法,将DC-DC开关变换器分为不同的模块,如输入滤波器、开关型切换器、输出滤波器等。
在每个模块中,采用相关的基本公式进行描述,并确定相应的系统参数。
2. 控制策略的设计控制策略对DC-DC开关变换器的稳定性和性能具有重要影响。
本研究将通过分析DC-DC开关变换器的工作原理,设计出恰当的控制策略。
具体来说,将研究开关频率控制、脉宽调制等控制方法,以确保输出电压的稳定性和纹波的最小化。
3. 数字仿真分析本研究将通过仿真软件进行数字仿真分析,模拟DC-DC开关变换器各种工作场景,包括小负载、大负载等。
首先,通过纯电阻负载、电容滤波负载等简单负载场景,验证模型的正确性。
然后,分析不同工作条件下DC-DC开关变换器效率、输出纹波、电压稳定性等重要性能指标。

第4章 开关变换器的时间平均等效电路开关变换器的状态空间平均建模和分析方法存在计算复杂、物理概念不清晰和不直观的缺点。
为了简化开关变换器的建模和分析,更直观、方便的分析开关变换器电路,有必要研究开关变换器的等效电路建模和分析方法。
本章所讨论的开关变换器的时间平均等效电路(Time Averaging Equivalent Circuit, TAEC)建模和分析方法,可以有效简化开关变换器的建模与分析过程。
开关变换器时间平均等效电路建模和分析方法的关键是采用受控电压源或者受控电流源等效替代开关变换器中的开关元件,得到电路结构不变的等效电路,从而可以很方便地使用基本的电路分析方法对开关变换器的直流稳态和交流小信号特性进行分析。
4.1 开关变换器的时间平均等效电路原理在讨论开关变换器时间平均等效电路建模和分析方法之前,先做如下假定: (1) 开关变换器是唯一可解的; (2) 开关变换器工作于周期稳态;(3) 开关变换器的开关频率f s 远大于开关变换器的最大特征频率f 0,即f s >> f 0。
在上述假设条件下,可以对开关变换器进行时间平均等效变换。
N CN SN SN C (a) (b)图4.1 开关变换器及其时间平均等效开关变换器时间平均等效电路建模分析的基本思想是:将开关变换器中所有开关元件抽取出来,形成线性时不变动态子网络N C 和开关子网络N S ,如图4.1(a)所示。
当开关变换器满足上述条件(1) ~ (3)时,可以分别采用受控电压源或受控电流源代替开关子网络N S 中的开关元件,得到由受控电压源和受控电流源构成的等效开关子网络N 'S ,如图4.1(b)所示。
当受控电压源或受控电流源的值分别是一个开关周期内它所代替的开关元件两端的电压或流过该开关元件的电流平均值,且在等效变换过程中,没有形成电流源(电感)割集和电压源(电容)回路,则在时间平均意义下,开关变换器N 可以等效为由线性时不变动态子网络N C 和等效开关子网络N 'S 构成的开关变换器时间平均等效电路。

I. 引言现代电子设备和电子系统通常由高密度、高速度的电路组成,这样的电路具有低压大电流的特性。
为了带动这样的负载,电源必须能在一个很宽的电流范围内提供稳定的电压,其稳态及暂态的整流特性也必须相当出色。
建模与仿真在现代DC-DC变换器的设计过程中扮演了很重要的角色。
它能让工程师在制作实际电路之前评估变换器的性能。
因此,我们可以在设计之初就发现并更正可能存在的设计缺陷,以提高生产率并节约生产本钱。
DC-DC变换器的建模和仿真在过去的十年里是一个热点[1]。
一般来说,变换器建模方法有两种:开关模型、平均模型。
在开关模型中,模型仿真了变换器的开关动作,仿真波形是包含了开关纹波的波形,这与实际看到的波形很相似。
而平均模型只仿真了变换器的平均特性,仿真波形也是平滑而连续的,这个波形代表了平均值而非实际值。
众所周知,对平均模型进展仿真要比开关模型快。
因此,平均模型常用于变换器动态性能的总体评估。
在过去,平均模型的仿真主要是用SPICE来完成的[2]。
SPICE的缺点在于仿真的对象必须是电路的形式,如果模型原型是复杂的方程式,那么要花费很大的精力将其转换成等效的电路形式。
尽管SPICE的新版本也开场支持建立纯数学模型,但是改善仍然有限。
最近,参考文献[3]介绍了一个不错的可以用在DC-DC变换器建模和仿真方面的工具——SIMULINK[4]。
然而,作者使用的变换器模型是线性化的,在大信号条件下,这个模型的仿真效果并不理想。
为了克制上述缺点,本论文讨论了如何应用SIMULINK在大信号条件下对DC-DC变换器进展平均模型的建模与方针。
本文拓展了文献[3]的研究,在变换器的功率和控制局部使用了非线性化的模型,从而改良了模型在大信号条件下的仿真效果。
下面将分别讨论Buck变换器的非线性化的模型,及相关的三个输出电压控制策略。
A. Buck变换器主电路拓扑Buck变换器主拓扑如图1所示:图1 Buck变换器Fig.1. Buck Converter在电流连续的模式下〔CCM〕——即开关开通的时候,电感电流连续——变换器表现为两个电路状态。


DC―DC开关变换器的建模与非线性行为控制一、Buck-Boost变换器工作原理Buck-Boost变换器电路如图1(a)所示。
Buck-Boost变换器功率级工作原理:当功率开关管S导通时,二极管D受反向电压关断,电感电流>上升。
当上升达到参考电流I时,S断开,>通过D进行续流,此时D导通。
如果在下一个时钟脉冲到来时大于0,则电路工作于连续导电模式(CCM),电路波形图1(b)所示;如果在下一个时钟脉冲到来前已降到0,则电路工作于不连续导电模式(DCM),此时开关S和D都关断,电路波形图1(c)所示。
控制级工作原理:将电感电流的采样值与参考电流I输入比较放大器A(其放大系数为K),得到误差信号e=(I-),该误差信号与锯齿波信号相比较,控制输出信号调节占空比D,进而控制开关S的导通时。
二、Buck-Boost变换器非线性行为在进行Buck-Boost变换器非线性行为分析前,做如下假设:(1)负载上的电压V恒定不变,可看作是一个电压源。
在实际电路中只要滤波电容足够大,这一假设是成立的;(2)变换器中所有器件均为理想器件,忽略其寄生参数。
1、连续导电模式在t=t(n=0,1,2,…)时刻,S闭合。
此时系统的微分方程为:(1)在t=t+DT(n=0,1,2,…)(D为系统的占空比)时刻,S 断开,此时系统的微分方程为:(2)当电感电流达到参考电流值时,电路开关S由导通转换为关断。
电感电流在时刻的采样值与基准电流I输入比较器A,A的反馈倍数为K,系统的采样控制方程为:(3)en输入PWM控制器,与锯齿波相比较,形成的占空比规律如下:(4)采用A开关映射的数据采样方法,即在开关S闭合的时刻采样数据。
设在t=tn(n=0,1,2…)和t=tn+T (n=0,1,2…)时刻电感电流采样值分别为in,in+1,则系统的离散方程为:(5)将式(3)和式(4)代入式(5),得:(6)其中:式(6)即为系统CCM的离散迭代方程。

第51卷第10期电力系统保护与控制Vol.51 No.10 2023年5月16日Power System Protection and Control May 16, 2023 DOI: 10.19783/ki.pspc.221314考虑谐波耦合的多变流器并网系统建模及交直流谐波交互特性分析林顺富1,李 寅1,戴烨敏2,杨 帆1,边晓燕1,李东东1(1.上海电力大学电气工程学院,上海 200090;2.国网上海市电力公司青浦供电公司,上海 201799)摘要:新型电力系统中高比例可再生能源和高比例电力电子设备接入的特征带来异于传统电网下的谐波交互问题,多变流器拓扑的谐波耦合交互特性亟待研究。
首先,基于谐波状态空间(harmonic state space, HSS)对多变流器并网系统(multiple grid-connected-converter system, MGCCS)建立考虑谐波耦合的谐波传递函数矩阵模型,综合考虑了系统各控制环节对状态变量的影响以及变流器的级联、并联。
其次,基于所建HSS模型明确定义谐波耦合系数,并用于揭示多变流器拓扑的谐波耦合机理,分析级联、并联变流器谐波交互特性。
然后,应用谐波耦合系数量化分析MGCCS中滤波电感、电流环、锁相环等关键参数对系统谐波交互的影响。
最后,将HSS模型和Matlab/Simulink 模型、RT-LAB模型的结果进行对比,验证了所建HSS模型的精确性,以及谐波耦合系数理论应用于系统交直流谐波交互分析的有效性。
关键词:多变流器并网系统;交直流谐波交互;谐波状态空间;谐波耦合系数;并网电流Modeling of a multiple grid-connected-converter system considering harmonic coupling andanalysis of AC/DC harmonic interaction characteristicsLIN Shunfu1, LI Yin1, DAI Yemin2, YANG Fan1, BIAN Xiaoyan1, LI Dongdong1(1. College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China; 2. Qingpu PowerSupply Company of State Grid Shanghai Municipal Electric Power Company, Shanghai 201799, China) Abstract: The characteristics of high penetration of renewable energy and high proportion of power electronic equipment in new power systems bring a harmonic interaction problem. This is different from traditional power systems. The harmonic coupling interaction characteristics of the multi-converter topology need to be studied. First, based on the harmonic state space (HSS), the harmonic transfer function matrix model considering harmonic coupling is established for the multiple grid-connected-converter system (MGCCS). The model comprehensively considers the influence of each control link of the system on the state variables as well as the factors of cascade and parallel converters. Second, the harmonic coupling coefficient is defined based on the established HSS model. This is used to reveal the harmonic coupling mechanism of the multi-converter topology, and analyze the harmonic interaction characteristics of the cascade and parallel converters. Then, the harmonic coupling coefficient is used to quantify the influence of key parameters such as filter inductor, current loop and phase-locked loop on the harmonic interaction of MGCCS. Finally, the results of the HSS model, Matlab/Simulink model and RT-LAB model are compared to verify the accuracy of the proposed HSS model and the effectiveness of the harmonic coupling coefficient theory applied to the AC/DC harmonic interaction analysis of the system.This work is supported by the National Natural Science Foundation of China (No. 51977127).Key words: multiple grid-connected-converter system; AC/DC harmonic interaction; harmonic state space;harmonic coupling coefficient; grid-connected current0 引言在“双碳”目标的背景下,以高渗透率的可再基金项目:国家自然科学基金项目资助(51977127);上海市科学技术委员会项目资助(19020500800);上海市教育发展基金会和上海市教育委员会“曙光计划”项目资助(20SG52) 生能源、高比例的电力电子设备、高速增长的新型负荷为主要特征的新型电力系统逐步形成[1-4]。
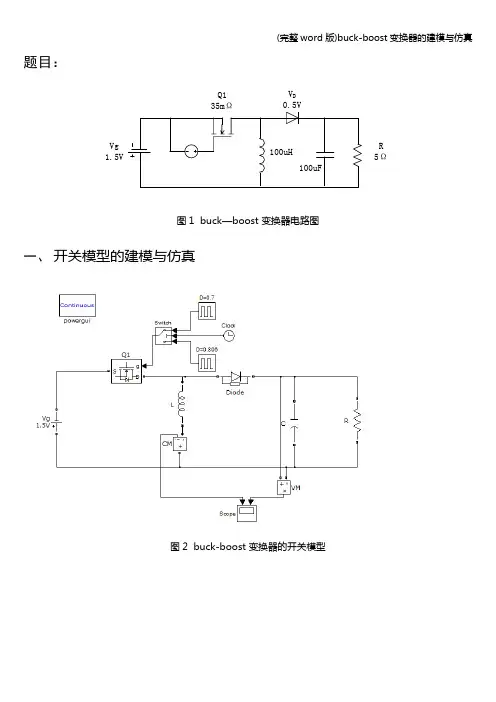
题目:Vg 1.5VQ135mΩ100uH100uFR5ΩV D0.5V图1 buck—boost 变换器电路图一、开关模型的建模与仿真图2 buck-boost 变换器的开关模型占空比由0.806变化到0.7的电感电流波形占空比由0.806变化到0.7的电容电压波形图3 buck —boost 变换器的开关模型的仿真二、 大信号模型与仿真1、 开关导通时:Vg 1.5VR on35m ΩV-图4 开关导通时的工作状态此时,电感电压和电容电流方程:(t)v (t)v (t)(t)(t)(t)(t)L g on c di L i R dtdv v i C dt R ⎧==-⎪⎪⎨⎪==-⎪⎩2、 开关断开时:100uH100uFVi c+-0.5Vi图5 开关断开时的工作状态此时,电感电压和电容电流方程:(t)v (t)(t)(t)(t)(t)(t)L D cdi L V v dtdv v i C i dt R ⎧==--⎪⎪⎨⎪==-⎪⎩3、平均方程电源电压、电感电流、电容电压变化的不大均为低频信号,则(t)(t)g g v v = ;(t)(t)i i =;v(t)v(t)=又因为:(t)v (t)L d i L dt= (t)(t)c d v i Cdt= 则有,电感电压平均方程:()()'v (t)d(t)v (t)(t)+d (t)(t)L g on D i R V v =---电容电流平均方程:''(t)(t)(t)(t)d(t)()d (t)((t))=d (t)(t)c v v v i i R R R=-+--+ 输入电流平均方程:g (t)d(t)(t)i i =4、大信号模型:()()''g (t)d(t)v (t)(t)+d (t)(t)d (t)(t)=d (t)(t)(t)d(t)(t)g on D d i L i R V v dt v v C i dt R i i ⎧=---⎪⎪⎪-+⎨⎪⎪=⎪⎩由方程可得到三个等效电路:-+-+-+g (t)i v (t)g (t)v D (t)i 'D (t)i d (t)v Cdt(t)d i Ldt'(0.5D )VonDR '(t)D v v (t)g D 图6buck-boost 变换器的大信号模型的等效电路大信号模型的仿真电路:图7 大信号模型仿真电路图大信号模型的仿真波形:电感电流随占空比变化的波形电容电压随占空比变化的波形图8 大信号模型仿真波形图三、 小信号模型假设,gv (t)=V +v (t)d(t)=D+d(t)(t)=(t)v(t)=V+v(t)(t)=(t)g g g g g i I i i I i ΛΛΛΛΛ⎧⎪⎪⎪⎪⎨+⎪⎪⎪⎪+⎩ 且各变量的扰动值远小于其稳态值。
详解:开关电源的小信号建模开关电源的反馈环路设计是开关电源设计的一个非常重要的部分,它关系到一个电源性能的好坏。
要设计一个好的环路,必须要知道主回路的数学模型,然后根据主回路的数学模型,设计反馈补偿环路。
本文想重点介绍下主回路的数学建模方法。
首先来介绍下小信号的分析法。
开关电源是一个非线性系统,但可以对其静态工作点附近进行局部线性化。
这种方法称为小信号分析法。
以一个CCM模式的BOOST电路为例,其增益为:其增益曲线为:其中M和D之间的关系是非线性的。
但在其静态工作点M附近很小的一个区域范围内,占空比的很小的扰动和增益变化量之间的关系是线性的。
因此在这个很小的区域范围内,我们可以用线性分析的方法来对系统进行分析。
这就是小信号分析的基本思路。
因此要对一个电源进行小信号建模,其步骤也很简单,第一步就是求出其静态工作点,第二步就是叠加扰动,第三步就是分离扰动,进行线性化,第四步就是拉氏变换,得到其频域特性方程,也就是我们说的传递函数。
要对一个变换器进行小信号建模,必须满足三个条件。
首先要保证得到的工作点是“静”态的。
因此有两个假设条件:1,一个开关周期内,不含有低频扰动。
因此叠加的交流扰动小信号的频率应该远远小于开关频率。
这个假设称为低频假设2,电路中的状态变量不含有高频开关纹波分量。
也就是系统的转折频率要远远小于开关频率。
这个假设称为小纹波假设。
其次为了保证这个扰动是在静态工作点附近,因此有第三个假设条件:3,交流小信号的幅值必须远远小于直流分量的幅值。
这个称为小信号假设。
对于PWM模式下的开关电源,通常都能满足以上三个假设条件,因此可以使用小信号分析法进行建模。
对于谐振变换器来说,由于谐振变换器含有一个谐振槽路。
在一个开关时区或多个开关时区内,谐振槽路中各电量为正弦量,或者其有效成分是正弦量。
正弦量的幅值是在大范围变化的,因此在研究PWM型变换器所使用的“小纹波假设”在谐振槽路的小信号建模中不再适用。
三相电压型PWM变换器开关周期平均模型第三章3.2.6基本拓扑Vm 为输入线电压峰峰值Sap,Snp…代表开关函数dc mV V >{}1;,,i ip in s s s i a b c ==−(,)bc bc bc dc v f s v =(,)bc bc bc dc v f s v =定义:{}1; ,,ip in s s i a b c +=求下列关系(,)ab ab ab dc v f s v =(,)ca ca ca dc v f s v =(,,,)dc i ij a b c i f s i i i =低压侧和高压侧电量与开关函数之间的关系各种关系的矢量形式定义矢量:ab a b l l bc b c ca c a v v v v v v v v v v −⎡⎤⎡⎤−⎢⎥⎢⎥⎢⎥⎢⎥==−⎢⎥⎢⎥⎢⎥⎢⎥−⎣⎦⎣⎦ab a b l l bc b c ca c a s s s s s s s s s s −⎡⎤⎡⎤−⎢⎥⎢⎥⎢⎥⎢⎥==−⎢⎥⎢⎥⎢⎥⎢⎥−⎣⎦⎣⎦13ab a b l l bc b c ca c a i i i i i i i i i i −⎡⎤⎡⎤−⎢⎥⎢⎥⎢⎥⎢⎥==−⎢⎥⎢⎥⎢⎥⎢⎥−⎣⎦⎣⎦l l l l dc T dc l l l l v s v i s i −−−−⎧=⎪⎪⎨⎪=⎪⎩则比较BUCK 电路L dc dc L v sv i si ⎧=⎪⎪⎨⎪=⎪⎩三相PWM整流器状态空间方程三相PWM整流器开关周期平均模型等效电路与BUCK电路平均模型比较⎧⎪113311l l dc L L l l L L d v v L L i v C RC −−−−−=−与BUCK电路等效电路比较dq 旋转坐标系下的三相PWM 变流器模型•在基波频率旋转的三相旋转坐标系中,三相对称平衡电量将成为直流量,这样可以简化三相系统的开关周期平均模型•将三相静止坐标系下的电量x 投影到以基波频率旋转的坐标系dq0下wtd qacb0dq abcx Tx =2fωπ=f 为电网基波频率1abc dq x T x −=dq0下PWM整流器的状态方程模型等效电路由于因此,0轴对应方程可略去模型等效电路三相PWM整流器小信号模型•小信号模型是指其静态工作点附近的小信号线性化模型。
第五章 开关变换器的状态空间平均建模开关变换器是通过调整开关器件的工作状态实现开关变换器输出电压的调整,在一个开关周期内,开关变换器是一个周期性时变电路,但在每一个开关工作状态,开关变换器又可以看作是一个线性电路。
因此,我们不能用常规的线性电路理论对开关变换器进行分析,而必须研究适用于开关变换器的建模分析方法。
5.1 开关变换器的状态空间平均模型 5.1.1 开关变换器的状态空间方程及其近似解对于一个在开关周期T 内有两个开关工作状态的开关变换器,我们可以分别写出它在每一个开关工作状态的状态方程,并进行求解。
工作状态1:在每一个开关周期的[0,DT ]时间段,开关变换器的状态方程为:d ()()()d ()t t t t t =+11x A x B u (5-1a )工作状态2: 在每一个开关周期的[DT ,T ]时间段,开关变换器的状态方程为:d ()()d (t)t t t=+22x A x B u (5-1b)其中:(t)x 是状态向量;()t u 是输入向量;A 1,A 2,B 1,B 2分别是工作状态1和工作状态2对应的状态矩阵和输入矩阵。
(I )开关工作状态1对应的状态方程的解为1110()0d tte t e ττ⎰A A u x(t)=x()+B (5-2)当开关变换器的开关频率(1/S f T =)远大于状态方程的特征频率0f ,即0S f f >>时,存在下述线性近似关系111DT DT e +≈A A (5-3)将(5-3)代入(5-2),可得1110011()()0()d 0d DTDTDT DT et DT et e ττττ+=+⎰⎰A A A 1I A B u x()=x()+B u x() (5-4a )当开关变换器的输入变量()t u 在一个开关周期内是常数,或相对于开关频率是慢变换量时,可以用()t u 在一个开关周期内的平均值u 等效,于是,由式(5-4a )可得1221120DT DT D T DT e ++A 11A x()=x()B u B u (5-4b )对于0S f f >>,可以忽略式(5-4b )中的2T 项,从而得到下述线性近似关系110DT DT DT e +A u x()=x()B (5-4c )(II )开关工作状态2对应的状态方程的解为22()()d tDTt DT e t eDT ττ-⎰A 2A u x(t)=x()+B (5-5)同理,由式(5-6)可得:112221212()00''''+'=+T T TTTD D D D D D T D T T e e DT eeDT eA A A A A uu u ux()=B B x()+x()+B B (5-6)式(5-6)中2121)(T D D T DT DT e ''=+A u u A B I B (5-7)忽略式(5-7)中的2T 项,可得21211)(T D D T DT DT DT e ''==+A u u u A B I B B (5-8)将式(5-8)代入式(5-6),得12)(12)0(T D D T T e D D +'+'A A u x()=x()+B B (5-9)(5-9)对应的微分方程为:1212)d d ()(D D D tt t D ''++A A u x()=x()+B B (5-10)其中t x()为开关变换器在一个开关周期内状态变量的平均值,(5-10)即为描述开关变换器在一个开关周期内的状态空间平均方程。
值得注意的是,在上述分析过程中,我们做了两个基本的假定:(1)开关变换器的开关频率(1/S f T =)远大于状态方程的特征频率0f ,即0S f f >>(2)开关变换器的输入变量()t u 在一个开关周期内是常数,或是相对于开关频率的慢变换量。
上述假定,对PWM 开关变换器是始终成立的。
5.1.2 开关变换器的状态空间平均方程上面我们分析了开关变换器在一个开关周期内两个开关工作状态的状态方程,及其近似解的表达式。
类似地,我们可以得到描述开关变换器所有变量行为的状态方程和输出方程及其平均等效方程。
当开关变换器工作于电感电流连续模式时,开关变换器在一个开关周期内存在两个开关工作状态,我们可以针对每一个开关工作状态,建立其对应的状态方程和输出方程。
工作状态1:在每一个开关周期的[0,dT ]时间段,开关管导通,二极管关断,在这一时间段内,开关变换器的状态方程和输出方程为:d ()()()d ()()()()t t t t t t t t =+=+1111x A x B u y C x E u (5-11a ) 工作状态2: 在每一个开关周期的[dT ,T ]时间段,开关管关断,二极管导通,在这一时间段内,开关变换器的状态方程和输出方程为:d ()()d ()()()(t)t t tt t t =+=+2222x A x B u y C x E u (5-11b) 其中:(t)x 是状态向量;()t u 是输入向量;()t y 是输出向量;A 1,A 2,B 1,B 2分别是工作状态1和工作状态2对应的状态矩阵和输入矩阵;C 1,C 2,E 1,E 2分别是工作状态1和工作状态2对应的输出矩阵和传递矩阵。
式(5-11)描述了开关变换器在一个开关周期内的状态变量。
当:(1)开关变换器的开关频率远大于开关变换器的特征频率时,可以认为开关变换器的状态变量在一个开关周期内保持不变;此外,当开关变换器的输入向量()t u 在一个开关周期内保持不变,或是相对于开关频率的慢变化量时,在一个开关周期内,状态变量(t)x 和输入变量()t u 可以分别用它们在一个开关周期内的平均值()t x 和()t u 近似。
则通过在一个开关周期内对所有变量进行时间平均(加权平均),可以得到开关变换器在一个开关周期内的状态空间平均方程为:d ()()(()())()(()())d t d t t t d t t t t'=+++1122x A x B u A x B u (5-12a) 类似地,我们可以得到开关变换器在一个开关周期内的平均输出方程为:()()(()())()(()())t d t t t d t t t '=+++1222y C x E u C x E u (5-12b)其中()1()d t d t '=-将式(5-12)重新组合成标准的线性连续系统的状态空间方程后,得到开关变换器在一个开关周期内的平均状态方程和平均输出方程d ()(()())()(()())()d ()(()())()(()())()t d t d t t d t d t t t t d t d t t d t d t t ''=+++''=+++12121212x A A x B B u y C C x E E u (5-13) 其中()t x ,()t u 和()t y 是状态向量,输入向量和输出向量在一个开关周期内的时间平均值,()d t 是开关控制脉冲的占空比。
图5-1给出了在一个开关周期内,状态变量()t x 在工作状态1和工作状态2的变化率与在一个开关周期内状态变量的净变化率之间的关系。
从图5-1可以看出,当开关变换器的开关频率远大于电路的特征频率,即状态变量在一个开关周期内的变化很小时,可以用一个开关周期内状态变量的平均值()t x 很好的近似等效状态变量的变化。
x x (t)S S图5-1 状态变量变化的直线近似式(5-13)所描述的开关变换器的状态空间平均模型可以表示成标准的状态方程形式d ()()()d ()()()t t t tt t t =+=+x Ax Bu y Cx Eu (5-14a) 其中1D D D D D D D D D D'=+'=+'=+'=+'=-12121212A A A B B B C C C E E E (5-14b) 比较式(5-14)和(5-11)可以发现,在开关变换器的状态空间平均模型中,状态方程的状态矩阵A 和输入矩阵B 分别是对应工作状态的状态矩阵A 1,A 2和输入矩阵B 1,B 2的加权平均值;输出方程的输出矩阵C 和传递矩阵E 分别是对应工作状态的输出矩阵C 1,C 2和传递矩阵E 1,E 2的加权平均值。
5.1.3 开关变换器的直流稳态和交流小信号等效方程基于式(5-13)所给出的开关变换器的状态空间平均方程,我们可以对开关变换器的直流稳态和交流小信号特性进行分析。
当开关变换器的输入变量()t u 和控制变量()d t 存在小信号扰动时,即ˆ()()t +t =u U u, ˆ()()d t D d t =+,ˆ()()d t D d t ''=- (5-15a) 时,将引起开关变换器中的状态变量和输出变量的小信号扰动,即ˆ()()t t =+x X x , ˆ()()t t =+y Y y (5-15b) 其中X ,U ,Y ,D 分别是()t x ,()t u ,()t y ,()d t 的直流分量;ˆx,ˆ()t u ,ˆ()t y ,ˆ()d t分别是()t x ,()t u ,()t y ,()d t 的交流小信号分量。
对于小信号扰动,我们有ˆx<<X ,ˆ()t u <<U ,ˆ()t y <<Y ,ˆ()d t <<D (5-15c) 则在存在小信号扰动时,开关变换器的状态空间平均方程为ˆd [()]ˆˆˆ{[()][()]}{()}d ˆˆˆ{[()][()]}{()} t D d t D d t t t D dt D d t t '=++-'+++-1212X +x A A X +x B B U +u (5-16a)ˆˆˆˆ(){[()][()]}{()}ˆˆˆ{[()][()]}{()} t D d t D d t t D d t D d t t 2'=++-'+++-E 121Y +y C C X +x E U +u(5-16b)式(5-16)经整理得到ˆd [()]ˆˆˆ()[]()d ˆˆˆ[()()]() t t d t t t t d t =+++12121212X +x AX +BU +Ax(t)+Bu (A -A )X +(B -B )U (A -A )x(B -B )u (5-17a)1ˆˆˆˆˆ()d t d +212Y +y(t)=CX +Cx(t)+(C -C )X (C -C )x (5-17b) 式(5-17)中存在两个与时间相关的变量ˆ()t x和ˆd 的乘积,是关于小信号扰动的非线性函数。