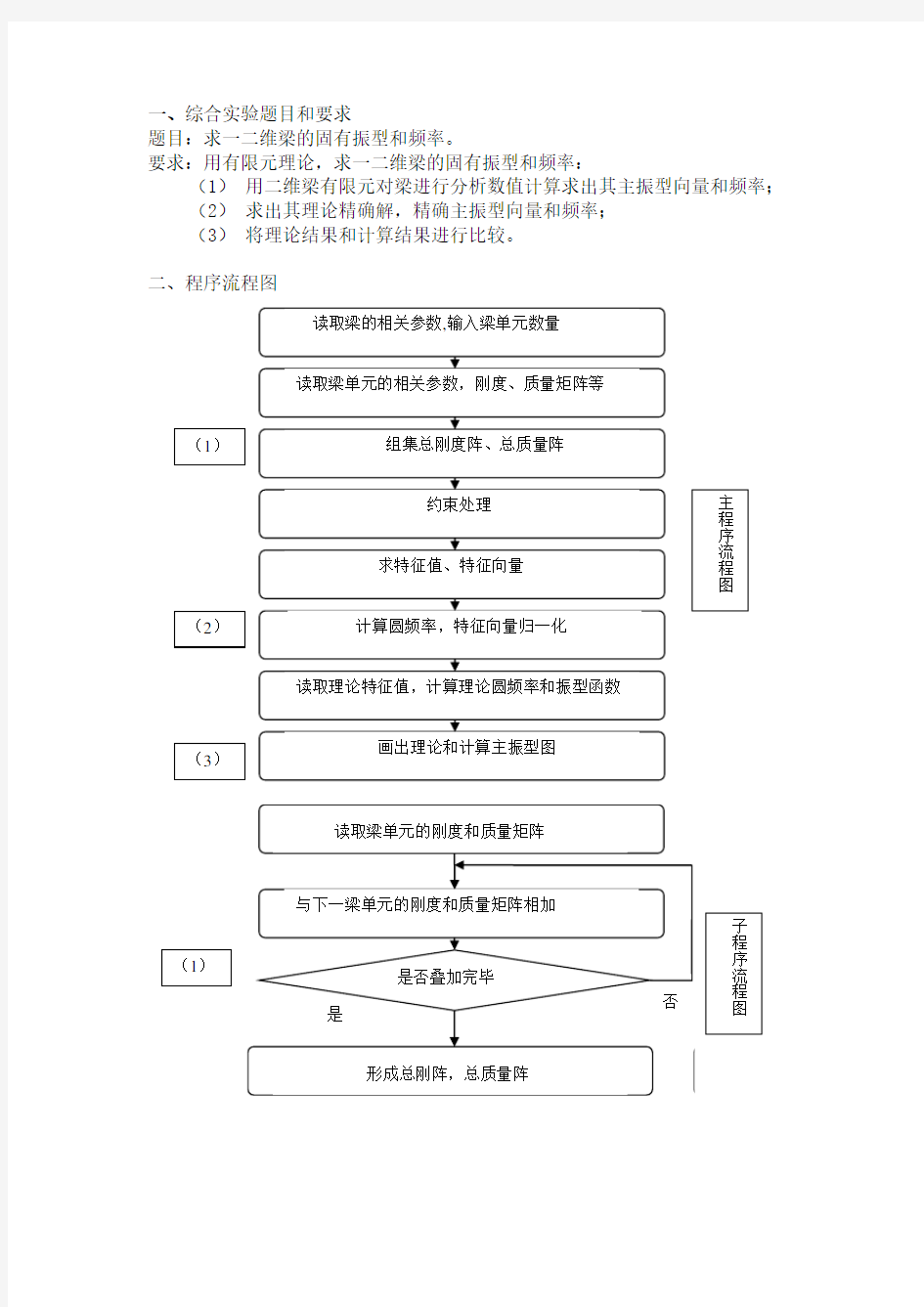

一、综合实验题目和要求
题目:求一二维梁的固有振型和频率。
要求:用有限元理论,求一二维梁的固有振型和频率:
(1) 用二维梁有限元对梁进行分析数值计算求出其主振型向量和频率; (2) 求出其理论精确解,精确主振型向量和频率; (3) 将理论结果和计算结果进行比较。
二、程序流程图
三、实验结果
1.前六阶振型
同一有限元数不同阶数比较(以有限元20为例)如下图所示:
00.10.20.30.40.50.60.70.80.9
一阶
-0.8
-0.6-0.4-0.200.20.40.60.81
二阶
-0.8
-0.6-0.4-0.200.20.40.60.81
三阶
-0.8
-0.6-0.4-0.200.20.40.60.8
四阶
-0.8
-0.6-0.4-0.200.20.40.60.81
五阶
-0.8
-0.6-0.4-0.200.20.40.60.81
六阶 四、实验分析
对于二维梁有限元的划分(以下只对二维梁而言),要根据需求精度进行合理划分,既兼顾精度,同时也兼顾计算量(随着计算精度的提高,单元数量增加,相应计算量也会增加,计算时间也会增加),经过试验随着单元数量增加,其计算精度也不段提高,当将梁分到七单元时,通过计算得到的主振型和频率和理论值吻合的非常好。当梁取一单元时(elementno=1),由于梁总体只有两自由度,故只能得出前两阶主振型;当梁取二单元时(elementno=2),由于梁总体有四自由度,故只能得出前四阶主振型;对于梁取三单元(elementno=3)以及三单元以上(elementno>3)时,梁总体有六自由度以及更高自由度,这里只画出前六阶主振型图。下六图是在elementno=20的情况下,通过计算,画出前六阶的主振型图(其中红线部分为理论主振型图,绿色五角星是计算在梁各单元节点处的振型,数量取决于梁单元划分的数目)。
五、源程序清单
clear all
close all
%各参数的设置
rou=2.7e3; %密度
A=1e-3;%横截面积
E=72e9; %弹性模量
L=1; %梁长
I=8.3333e-009;%截面惯性矩
elementno=input('输入有限元的数量:'); %有限元的数量
rodno=elementno+1;%节点数
alldimension=rodno*2;
l=L/elementno;
%单元刚度矩阵
ke=E*I/l^3*[12 -6*l -12 -6*l;
-6*l 4*l^2 6*l 2*l^2;
-12 6*l 12 6*l;
-6*l 2*l^2 6*l 4*l^2];
%单元质量矩阵
me=rou*A*l/420*[156 -22*l 54 13*l; -22*l 4*l^2 -13*l -3*l^2;
54 -13*l 156 22*l;
13*l -3*l^2 22*l 4*l^2];
K=zeros(alldimension,alldimension); M=zeros(alldimension,alldimension);
for i=1:elementno %总刚度矩阵和总质量矩阵
K(2*i-1,2*i-1)=ke(1,1)+K(2*i-1,2*i-1); K(2*i-1,2*i)=ke(1,2)+K(2*i-1,2*i);
K(2*i-1,2*i+1)=ke(1,3)+K(2*i-1,2*i+1) ;
K(2*i-1,2*i+2)=ke(1,4)+K(2*i-1,2*i+2) ;
K(2*i,2*i-1)=ke(2,1)+K(2*i,2*i-1);
K(2*i,2*i)=ke(2,2)+K(2*i,2*i);
K(2*i,2*i+1)=ke(2,3)+K(2*i,2*i+1);
K(2*i,2*i+2)=ke(2,4)+K(2*i,2*i+2);
K(2*i+1,2*i-1)=ke(3,1)+K(2*i+1,2*i-1) ;
K(2*i+1,2*i)=ke(3,2)+K(2*i+1,2*i);
K(2*i+1,2*i+1)=ke(3,3)+K(2*i+1,2*i+1 );
K(2*i+1,2*i+2)=ke(3,4)+K(2*i+1,2*i+2 );
K(2*i+2,2*i-1)=ke(4,1)+K(2*i+2,2*i-1) ;
K(2*i+2,2*i)=ke(4,2)+K(2*i+2,2*i);
K(2*i+2,2*i+1)=ke(4,3)+K(2*i+2,2*i+1 );
K(2*i+2,2*i+2)=ke(4,4)+K(2*i+2,2*i+2 ); M(2*i-1,2*i-1)=me(1,1)+M(2*i-1,2*i-1) ;
M(2*i-1,2*i)=me(1,2)+M(2*i-1,2*i);
M(2*i-1,2*i+1)=me(1,3)+M(2*i-1,2*i+ 1);
M(2*i-1,2*i+2)=me(1,4)+M(2*i-1,2*i+ 2);
M(2*i,2*i-1)=me(2,1)+M(2*i,2*i-1);
M(2*i,2*i)=me(2,2)+M(2*i,2*i);
M(2*i,2*i+1)=me(2,3)+M(2*i,2*i+1); M(2*i,2*i+2)=me(2,4)+M(2*i,2*i+2); M(2*i+1,2*i-1)=me(3,1)+M(2*i+1,2*i-1);
M(2*i+1,2*i)=me(3,2)+M(2*i+1,2*i); M(2*i+1,2*i+1)=me(3,3)+M(2*i+1,2*i+ 1);
M(2*i+1,2*i+2)=me(3,4)+M(2*i+1,2*i+ 2);
M(2*i+2,2*i-1)=me(4,1)+M(2*i+2,2*i-1);
M(2*i+2,2*i)=me(4,2)+M(2*i+2,2*i);
M(2*i+2,2*i+1)=me(4,3)+M(2*i+2,2*i+ 1);
M(2*i+2,2*i+2)=me(4,4)+M(2*i+2,2*i+
2);
end
Kcantalever=K(3:alldimension,3:alldime nsion);
Mcantalever=M(3:alldimension,3:alldim ension);
[V,D]=eig(Kcantalever,Mcantalever);
lanbuda=diag(D);%特征值
omega=sqrt(diag(D))
vstandard=zeros(elementno,elementno); %数值计算主振型的生成
for i=1:(alldimension-2)
Vstandard(:,i)=V(:,i)/V((alldimension-3) ,i);
for j=1:elementno
vstandard(j,i)=Vstandard(2*j-1,i);
%提取有纵向位移有关的向量元素形成新向量
end
end
lanbudar=[1.875 4.694 7.855
10.996 14.137 17.279]'
omegaexact=lanbudar.^2*sqrt(E*I/rou/ A)
x=0:0.01:1; xrod=linspace(1/elementno,1,elementno );
y1=zeros(101,6);
a=(sinh(lanbudar)-sin(lanbudar))./(cosh( lanbudar)+cos(lanbudar));
if (elementno<=3)
p=2*elementno;
else p=6;
end
for i=1:p
y1(:,i)=cosh(lanbudar(i)*x')-cos(lanbuda r(i)*x')-a(i).*(sinh(lanbudar(i)*x')-sin(l a nbudar(i)*x')); %理论主振型函数ystandardexact= y1(:,i)/ y1(101,i); %理论主振型归一化
figure(i)
plot(x,ystandardexact,'r') %理论主振型函数的绘制
hold on
plot(xrod,vstandard(:,i),'g*')
grid on
end
六、对本实验课的几点建议
首先,通过几周的MATLAB课程的学习,让我掌握了其基本的操作和命令,以及其Simulink仿真模块,对以后的学习增加了一个实用的数学工具。
其次,在完成作业的过程中进一步让我熟悉了该软件的应用,最关键的是应用到专业相关的题目求解中,对于车辆动态仿真的领域将于相关软件(如ADMAS)结合进行联合仿真,让我受益匪浅。
最后,在上课的过程中,由于机器较少,希望能增加一些机器,希望老师能提供一些除幻灯片外的其他关于MATLAB的学习资料。
总之,感谢游霞老师的悉心指导。
说明:在下面的数据处理中,如1 A,11d T,1δ,1ξ,1n T,1nω:表示第一次实 1 验中第一、幅值、对应幅值时间、变化率、阻尼比、无阻尼固有频率。第二 次和和三次就是把对应的1改成2或3.由于在编缉公式时不注意2,3与平 方,三次方会引起误会,请老师见谅!! Ap0308104 陈2006-7-1 实验题目:悬臂梁一阶固有频率及阻尼系数测试 一、实验要求以下: 1. 用振动测试的方法,识别一阻尼结构的(悬臂梁)一阶固有频率和阻尼系数; 2. 了解小阻尼结构的衰减自由振动形态; 3. 选择传感器,设计测试方案和数据处理方案,测出悬臂梁的一阶固有频率和阻尼 根据测试曲线,读取数据,识别悬臂梁的一阶固有频率和阻尼系数。 二、实验内容 识别悬臂梁的二阶固有频率和阻尼系数。 三、测试原理概述: 1,瞬态信号可以用三种方式产生,有脉冲激振,阶跃激振,快速正弦扫描激振。 2,脉冲激励用脉冲锤敲击试件,产生近似于半正弦的脉冲信号。信号的有效频率取决于脉冲持续时间τ,τ越小则频率范围越大。 3.幅值:幅值是振动强度的标志,它可以用峰值、有效值、平均值等方法来表示。 频率:不同的频率成分反映系统内不同的振源。通过频谱分析可以确定主要频率成分及其幅值大小,可以看到共振时的频率,也就可以得到悬臂梁的固有频率 4、阻尼比的测定 自由衰减法: 在结构被激起自由振动时,由于存在阻尼,其振幅呈指数衰减波形,可算出阻尼比。一阶固有频率和阻尼比的理论计算如下:
11 3 3 44 4 2 3.515(1) 2=210 ;70;4;285;7800 ; ,12 12 ,, Ix = 11.43 c m Iy= 0.04 c m 0.004 2.810,,1x y y f k g E p a b m m h m m L m m m a b a b I I I m m E L π ρρ-----------?===== = ?=?固x y = 式惯性矩:把数据代入I 后求得 载面积:S =b h =0.07m 把S 和I 及等数据代入()式, 求得本41.65() H Z 固理悬臂梁理论固有频率f = 阻尼比计算如下: 2 2 2 1 111 220, 2,........ln , ,22;n d n n n d n d n T i i i j j i i i i j i i i j i n d i j n d n d d d d x d x c k x d t d t c e A A A A A T A T T ξωξωωξωωωξωωηη δξωωωωωπδπξ++ -++ +++ + ++=++===≈== ? ?? ==≈2 二阶系统的特征方程为S 微分方程:m 当很少时,可以把。A 减幅系数=而A A A A A 1则:= j 又因为所以==,所以=即可知δξπ = 2 在这个实验中,我们使用的是自由衰减法,以下是实验应该得到的曲线样本及物理模型。
简支梁横向振动的固有频率及振型函数的推导 一.等截面细直梁的横向振动 取梁未变形是的轴线方向为X 轴(向右为正),取对称面内与x 轴垂直的方向为y 轴(向上为正)。梁在横向振动时,其挠曲线随时间而变化,可表示为 y=y(x,t) (1) 除了理想弹性体与微幅振动的假设外,我们还假设梁的长度与截面高度之比是相当大的(大于10)。故可以采用材料力学中的梁弯曲的简化理论。根据这一理论,在我们采用的坐标系中,梁挠曲线的微分方程可以表示为: 22y EI M x ?=? (2) 其中,E 是弹性模量,I 是截面惯性矩,EI 为梁的弯曲刚度,M 代表x 截面处的弯矩。挂怒弯矩的正负,规定为左截面上顺时针方向为正,右截面逆时针方向为正。关于剪力Q 的正负,规定为左截面向上为正,右截面向下为正。至于分布载荷集度q 的正向则规定与y 轴相同。在这些规定下,有: M Q Q q x x ??==??, (3) 于是,对方程(2)求偏导,可得: 222222(EI )(EI )y M y Q Q q x x x x x x ??????====??????, (4) 考虑到等截面细直梁的EI 是常量,就有:
3434y y EI Q EI q x x ??==??, (5) 方程(5)就是在等截面梁在集度为q 的分部李作用下的挠曲微分方程。 应用达朗贝尔原理,在梁上加以分布得惯性力,其集度为 22 y q t ρ?=-? (6) 其中ρ代表梁单位长度的质量。假设阻尼的影响可以忽略不计,那么梁在自由振动中的载荷就仅仅是分布的惯性力。将式(6)代入(5),即得到等截面梁自由弯曲振动微分方程: 4242y y EI x t ρ??=--?? (7) 其中2 /a EI ρ=。 为求解上述偏微分方程(7),采用分离变量法。假设方程的解为: y(x,t)=X(x)Y(t) (8) 将式(8)代入(7),得: 22424 1Y a d X Y t X dx ?=-? (9)
上海第二工业大学 名称:传感器与测试技术技能实习 专业:机械电子工程 班级:13机工A1 姓名: 学号:2013481 指导老师:杨淑珍孙芳方 实训地点:14#407
目录 一、技能实习内容及要求 (1) 二、总体方案设计 (2) 2-1. 测量原理 (2) 2-2. 测试系统组成 (2) 2-3. 激励方法 (3) 三、实验硬的件选用 (3) 3-1、悬臂梁 (3) 3-2.传感器 (4) 3-3、电荷放大器 (5) 3-4、采集卡 (6) 四、硬件电路的设计 (6) 五、测量软件设计 (9) 六、小结和体会 (16)
一、技能实习内容及要求 1-1. 内容: 设计一个测试悬臂梁固有频率的自动测试系统,悬臂梁如下所示: 具体技术要求: 能显示相应所采集到的波形图、频谱图等相关图 能显示固有频率 能对固有频率进行超限报警,上下限制用户可设定 生成当前测试报告,(包括相应波形图和固有频率值以及合格状态) 1-2. 实训要求: 1、提出设计方案(提出测量原理,传感器选用和安装,构建测试系统) 2、设计测量电路(包括放大,滤波电路,制作滤波电路) 3、测试软件设计:利用Labview或其它开发程序(VB、VC等),设计测量软件进行数据采集和分析 4、调试 5、撰写实训报告 1-3. 报告要求: 1.实训内容 2.撰写总体设计方案 3.硬件选用(包括传感器、采集卡的选用和安装等) 4.电路设计(包括测量电路设计,系统总电路)
5.测量软件设计(包括软件设计流程图,各功能实现方法和代码,包括个主程序,子程序描述以及相应的重要参数设置如采样通道,采样频率,采样点数) 6.小结和体会(可包含调试中遇到的问题) 二、总体设计方案 2-1.测量原理: 在测试的过程中,通过脉冲锤敲击悬臂梁的横梁产生一个脉冲信号。信号会逐渐衰减,在衰减过程中会有一个时刻衰减到的频率和悬臂梁的固有频率相同,我们要找到的就是这个相同的频率,这个频率与悬臂梁固有频率形成共振,那时候的复制达到最大,用labview分析这个值,就可以测出悬臂梁的固有频率。 2-2.测试系统的组成: 图1测试系统组成图 测试系统包括下述三个主要部分: 激励部分:
模态分析技术发展到今天已趋成熟,特别是线性模态理论(通常所说的模态分析均是指线性模态分析)方面的研究已日臻完善,但在工程应用方面还有不少工作可做。首先是如何提高模态分析的精度,扩大应用范围。增加模态分析的信息量是提高分析精度的关键,单靠增加传感器的测点数目很难实现,目前提出的一种激光扫描方法是大大增加测点数的有效办法,测点数目的增加随之而来的是增大数据采集与分析系统的容量及提高分析处理速度,在测试方法、数据采集与分析方面还有不少研究工作可做。对复杂结构空间模态的测量分析、频响函数的耦合、高频模态检测、抗噪声干扰……等等方面的研究尚需进一步开展。模态分析当前的一个重要发展趋势是由线性向非线性问题方向发展。非线性模态的概念早在1960年就由Rosenberg提出,虽有不少学者对非线性模态理论进行了研究,但由于非线性问题本身的复杂性及当时工程实践中的非线性问题并示引起重视,非线性模态分析的发展受到限制。近年来在工程中的非线性问题日益突出,因此非线性模态分析亦日益受到人们的重视。最近已逐步形成了所谓非线性模态动力学。关于非线性模态的正交性、解耦性、稳定性、模态的分叉、渗透等问题是当前研究的重点。在非线性建模理论与参数辨识方面的研究工作亦是当今研究的热点。非线性系统物理参数的识别、载荷识别方面的研究亦已开始。展望未来,模态分析与试验技术仍将以新的速度,新的内容向前发展。 模态振型是一个相对量,通常是一个列向量,二维以上的系统其模态振型不是一个数。一个数对应单模态,其数值无意义。某模态频率下的模态振型反映了在该模态频率下各自由度的相对位移的比值。如果系统的初始位移恰好等于模态频率下的模态振型(或与之成比例),则此时系统的自由响应中只会出现该模态频率。感谢欧阳中华教授的指点,我现在觉得自己当初确实对模态振型概念不清楚。模态振型是系统固有的振动形态,线性响应是振型线性叠加的结果,但振型之间是独立不耦合的。振型是个相对量,所以就有了多种振型归一划的方法。振型是个很重要的固有特征,正如楼上所说用于验证固有频率。 我觉得振型在判别你计算固有频率正确性是非常有用的,比如,通过有限元计算得到了模型的前十阶固有频率,试验模态分析也得到了低阶的固有频率,假设计算的某阶固有频率与试验的某阶固有频率非常接近,但是并不能马上说明他们是同一阶的,需要通过振型来判断。 其他的不知道,但是之所以引入模态的概念,之所以从物理坐标变换到模态坐标就是为了解耦,就是为了让其正交,这样方程才能解出来。从能量角度说,这样各个振型之间就没有能量的交换。 从数学上看,对响应函数级数展开后,其中的各项构成各阶模态,而级数展开形
实验题目:悬臂梁固有频率测试实验数据处理 一、实验要求以下: 1. 用振动测试的方法,识别一阻尼结构的(悬臂梁)一阶固有频率和阻尼系数; 2. 了解小阻尼结构的衰减自由振动形态; 3. 选择传感器,设计测试方案和数据处理方案,测出悬臂梁的一阶固有频率和阻尼 根据测试曲线,读取数据,识别悬臂梁的一阶固有频率和阻尼系数。 二、实验内容 识别悬臂梁的二阶固有频率和阻尼系数。 三、测试原理概述: 1,瞬态信号可以用三种方式产生,有脉冲激振,阶跃激振,快速正弦扫描激振。 2,脉冲激励用脉冲锤敲击试件,产生近似于半正弦的脉冲信号。信号的有效频率取决于脉冲持续时间τ,τ越小则频率范围越大。 3.幅值:幅值是振动强度的标志,它可以用峰值、有效值、平均值等方法来表示。 频率:不同的频率成分反映系统内不同的振源。通过频谱分析可以确定主要频率成分及其幅值大小,可以看到共振时的频率,也就可以得到悬臂梁的固有频率 实验步骤及内容 1,按要求,把各实验仪器连接好接入电脑中,然后在悬臂梁上粘紧压电式加速度传感器打开计算机,。。 2,打开计算机,启动计算机上的“振动测试及谱分析.vi ”。 3,选择适当的采样频率和采样点数以及硬件增益。点击LabVIEW 上的运行按钮(Run )观察由脉冲信号引起梁自由衰减的曲线的波形和频谱。 4,尝试输入不同的滤波截止频率,观察振动信号的波形和频谱的变化。 5,尝试输入不同的采样频率和采样点数以及硬件增益,观察振动信号的波形变化。 6,根椐最合适的参数选择,显示最佳的结果。然后按下“结束按钮,完成信号采集。最后我选择的参数是:采样频率 f为512HZ,采样点数N为512点。 s 7,记录数据,copy读到数据的程序,关闭计算机。
一、综合实验题目和要求 题目:求一二维梁的固有振型和频率。 要求:用有限元理论,求一二维梁的固有振型和频率: (1) 用二维梁有限元对梁进行分析数值计算求出其主振型向量和频率; (2) 求出其理论精确解,精确主振型向量和频率; (3) 将理论结果和计算结果进行比较。 二、程序流程图
三、实验结果 1.前六阶振型 同一有限元数不同阶数比较(以有限元20为例)如下图所示:
00.10.20.30.40.50.60.70.80.9 一阶 -0.8 -0.6-0.4-0.200.20.40.60.81 二阶 -0.8 -0.6-0.4-0.200.20.40.60.81 三阶
-0.8 -0.6-0.4-0.200.20.40.60.8 四阶 -0.8 -0.6-0.4-0.200.20.40.60.81 五阶 -0.8 -0.6-0.4-0.200.20.40.60.81 六阶 四、实验分析
对于二维梁有限元的划分(以下只对二维梁而言),要根据需求精度进行合理划分,既兼顾精度,同时也兼顾计算量(随着计算精度的提高,单元数量增加,相应计算量也会增加,计算时间也会增加),经过试验随着单元数量增加,其计算精度也不段提高,当将梁分到七单元时,通过计算得到的主振型和频率和理论值吻合的非常好。当梁取一单元时(elementno=1),由于梁总体只有两自由度,故只能得出前两阶主振型;当梁取二单元时(elementno=2),由于梁总体有四自由度,故只能得出前四阶主振型;对于梁取三单元(elementno=3)以及三单元以上(elementno>3)时,梁总体有六自由度以及更高自由度,这里只画出前六阶主振型图。下六图是在elementno=20的情况下,通过计算,画出前六阶的主振型图(其中红线部分为理论主振型图,绿色五角星是计算在梁各单元节点处的振型,数量取决于梁单元划分的数目)。 五、源程序清单 clear all close all %各参数的设置 rou=2.7e3; %密度 A=1e-3;%横截面积 E=72e9; %弹性模量 L=1; %梁长 I=8.3333e-009;%截面惯性矩 elementno=input('输入有限元的数量:'); %有限元的数量 rodno=elementno+1;%节点数 alldimension=rodno*2; l=L/elementno; %单元刚度矩阵 ke=E*I/l^3*[12 -6*l -12 -6*l; -6*l 4*l^2 6*l 2*l^2; -12 6*l 12 6*l; -6*l 2*l^2 6*l 4*l^2]; %单元质量矩阵
Open Journal of Acoustics and Vibration 声学与振动, 2019, 7(1), 12-19 Published Online March 2019 in Hans. https://www.doczj.com/doc/de11202057.html,/journal/ojav https://https://www.doczj.com/doc/de11202057.html,/10.12677/ojav.2019.71002 Analysis for Natural Frequency and Mode Shape of Wing Structure Liang Chen, Jinwu Wu, Hanqing Li College of Aero Engineering, Nanchang Hangkong University, Nanchang Jiangxi Received: Feb. 10th, 2019; accepted: Feb. 22nd, 2019; published: Mar. 1st, 2019 Abstract In this electronic document, the FEM is used to simulate and analyze the natural frequency and vi-bration mode of a certain UAV composite wing. By using the non-contact laser vibrometer equip-ment, in order to eliminate the influence of boundary conditions on the vibration characteristics of the wing structure, the vibration characteristics of the wing are measured by free boundary conditions, and the first 4 natural frequencies and vibrations of the composite wing are obtained. At the same time, the finite element simulation results are compared. The calculation results show that the simulation results are basically consistent with the experimental results. Keywords Wing Structure, Experimental Analysis, Natural Frequency, Mode Shape 某机翼结构的固有频率和振型分析 陈亮,吴锦武,李汉青 南昌航空大学飞行器工程学院,江西南昌 收稿日期:2019年2月10日;录用日期:2019年2月22日;发布日期:2019年3月1日 摘要 本文采用有限元和试验对某一无人机复合材料机翼的固有频率和振型进行仿真和实验分析。通过利用非接触式激光测振仪设备,为了消除边界条件对机翼结构振动特性的影响,采用自由边界条件进行了机翼振动特性测量,获得了复合材料机翼的前4阶固有频率和振型。同时对比了有限元仿真结果。计算结果表明,仿真结果与试验测试结果基本一致。
悬臂梁固有频率的计算 试求在0x =处固定、x l =处自由的等截面悬臂梁振动的固有频率(求解前五阶)。 解:法一:欧拉-伯努利梁理论 悬臂梁的运动微分方程为:4242(,)(,)+0w x t w x t EI A x t ρ??=??; 悬臂梁的边界条件为:2222(0)0(1),(0)0(2)0(3),(EI )0(4)x l x l dw w w w x x dx x x x ==???======???,; 该偏微分方程的自由振动解为(x,t)W(x)T(t)w =,将此解带入悬臂梁的运动微分方程可得到 1234(x)C cos sin cosh sinh W x C x C x C x ββββ=+++,(t)Acos t Bsin t T w w =+;其中2 4 A EI ρωβ= 将边界条件(1)、(2)带入上式可得13C 0C +=,24C 0C +=;进一步整理可得 12(x)C (cos cosh )(sin sinh )W x x C x x ββββ=-+-;再将边界条件(3)、(4)带入可得 12(cos cosh )C (sin sinh )0C l l l l ββββ-+-+=;12(sin sinh )C (cos cosh )0C l l l l ββββ--+-+=要 求12C C 和有非零解,则它们的系数行列式必为零,即 (cos cosh ) (sin sinh ) =0(sin sinh )(cos cosh ) l l l l l l l l ββββββββ-+-+--+-+ 所以得到频率方程为:cos()cosh()1n n l l ββ=-; 该方程的根n l β表示振动系统的固有频率:12 2 4 ()(),1,2,...n n EI w l n Al βρ==满足上式中的各 n l β(1,2,...n =)的值在书P443表8.4中给出,现罗列如下:123451.875104 4.6940917.85475710.99554114.1372l l l l l βββββ=====,,,,; 若相对于n β的2C 值表示为2n C ,根据式中的1n C ,2n C 可以表示为21cos cosh ()sin sinh n n n n n n l l C C l l ββββ+=-+;
悬臂梁固有频率的计算 令狐采学 试求在0x =处固定、x l =处自由的等截面悬臂梁振动的固有频率(求解前五阶)。 解:法一:欧拉伯努利梁理论 悬臂梁的运动微分方程为:4242 (,)(,) +0w x t w x t EI A x t ρ??=??; 悬臂梁的边界条件为: 2222(0)0(1),(0)0(2)0(3),(EI )0(4)x l x l dw w w w x x dx x x x ==???======???,; 该偏微分方程的自由振动解为(x,t)W(x)T(t)w =,将此解带入悬臂梁的运动微分方程可得到 1234(x)C cos sin cosh sinh W x C x C x C x ββββ=+++, (t)Acos t Bsin t T w w =+;其中2 4 A EI ρωβ= 将边界条件(1)、(2)带入上式可得13C 0C +=,24C 0C +=;进一步整理可得12(x)C (cos cosh )(sin sinh )W x x C x x ββββ=-+-;再将边界条件(3)、(4)带入可得 12(cos cosh )C (sin sinh )0C l l l l ββββ-+-+=; 12(sin sinh )C (cos cosh )0C l l l l ββββ--+-+=要求12C C 和有非零解,则
它们的系数行列式必为零,即 (cos cosh )(sin sinh ) =0(sin sinh ) (cos cosh ) l l l l l l l l ββββββββ-+-+--+-+ 所以得到频率方程为:cos()cosh()1n n l l ββ=-;该方程的根n l β表示振 动系统的固有频率:1 2 24()(),1,2,...n n EI w l n Al βρ==满足上式中的各n l β(1,2,...n =)的值在书P443表8.4中给出,现罗列如下: 123451.875104 4.6940917.85475710.99554114.1372 l l l l l βββββ=====,,,,;若相对于n β的2C 值表示为2n C ,根据式中的1n C ,2n C 可以表示为21cos cosh ( )sin sinh n n n n n n l l C C l l ββββ+=-+;因此 1cos cosh (x)C (cos x cosh x)(sin x sinh x),1,2,... sin sinh n n n n n n n n n n l l W n l l ββββββββ??+=---=??+?? 由此可得到悬臂梁的前五阶固有频率,分别将n=1,2,3,4,5带入可得: 1112 2222 2123444 1.875104() 4.694091()7.854757()EI EI EI Al Al Al ωωωρρρ===,,, 11 2 2 224544 10.995541()14.1372()EI EI Al Al ωωρρ==,; 法二、铁摩辛柯梁梁理论 1.悬臂梁的自由振动微分方程: 4242442224(,)(,)(1)0w x t w x t E w I w EI A I kG kG x t x t t ρρρ????+-++=?????; 边界条件:(0)(0)0w x x φ====(1),0x l x l w x x φ φ ==??-= =??(2);
模态振型是一个相对量,通常是一个列向量,二维以上地系统其模态振型不是一个数.一个数对应单模态,其数值无意义.某模态频率下地模态振型反映了在该模态频率下各自由度地相对位移地比值.如果系统地初始位移恰好等于模态频率下地模态振型(或与之成比例),则此时系统地自由响应中只会出现该模态频率. 感谢欧阳中华教授地指点,我现在觉得自己当初确实对模态振型概念不清楚.模态振型是系统固有地振动形态,线性响应是振型线性叠加地结果,但振型之间是独立不耦合地.振型是个相对量,所以就有了多种振型归一划地方法.振型是个很重要地固有特征,正如楼上所说用于验证固有频率. 文档来自于网络搜索 我觉得振型在判别你计算固有频率正确性是非常有用地,比如,通过有限元计算得到了模型地前十阶固有频率,试验模态分析也得到了低阶地固有频率,假设计算地某阶固有频率与试验地某阶固有频率非常接近,但是并不能马上说明他们是同一阶地,需要通过振型来判断. 文档来自于网络搜索 其他地不知道,但是之所以引入模态地概念,之所以从物理坐标变换到模态坐标就是为了解耦,就是为了让其正交,这样方程才能解出来. 从能量角度说,这样各个振型之间就没有能量地交换. 文档来自于网络搜索 从数学上看,对响应函数级数展开后,其中地各项构成各阶模态,而级数展开形式本身要求各个基函数是相互正交地,也就是说:其实是把响应函数放到了一个函数空间里,各个展开项系数相当于这个响应在此函数空间里地坐标.文档来自于网络搜索 因为个自由度以上地系统往往都有耦合现象,例如方程*^^*中地、不同时为对角阵.但是从求解地角度来说,我们又希望其中地每个方程都是独立地,那样我们就可以像求解单自由度系统一样求解.我们就想能否选到合适地坐标系,使得运动完全不耦合,即系统质量矩阵和刚度矩阵同时为对角矩阵,称这样地坐标系为主坐标系,而模态坐标正是我们要寻找地主坐标.固有振型地正交性是指(以自由度为例),第一阶固有振动引起地作用力在第二阶固有振动上所做地功为零,即两种固有振动间无弹性势能地交换.同时也可证明振型地各阶导数间也是正交地. 文档来自于网络搜索 就像不同地坐标系下,对同一运动系统地表述会很不一样,表述同一运动系统地振型模态也可以有很多物理量地坐标系,当然其中很多都是很复杂地,对解决实际问题是没有实际意义和帮助地,只有那个特殊地正交状态地模态坐标,才是最简单最有用地坐标,因为它能把系统解耦,,这个特殊地坐标称之为主坐标,对应主振型,这个状态可以把方程解开,把问题解决掉,,文档来自于网络搜索 各阶模态是互相正交是为了解耦,使问题最简化.类似向量地分解,比方说,一个平面内力向量地分解方式有很多种,但采用直角正交分解最方便. 文档来自于网络搜索 主要从以后地解方程组时候要解耦考虑吧 模态正交,具体表现在模态振型存在正交,请注意“存在”,而这种正交是线性系统模态地基本特性,准确地说是固有特性,正因为存在这种正交特性,带来了运算时地广义坐标下地耦合矩阵变为模态坐标中.文档来自于网络搜索 地解耦,计算变得简单. 注:(对上段话地个人理解:线性系统具有正交特性,人们利用线性系统地正交特性,对线性模态进行解耦,使问题简化.)文档来自于网络搜索 .任一阶主振型地惯性力在另一阶主振型作为虚位移上所做地虚功之和为零 .任一阶主振型地惯性力只在各自地振型上做功,在另外地主振型上不做功 这是正交相应地物理解释,是模态振型正交地物理形式,所以不能用物理含义去证明其相应地数学表达. 上面模态正交地数学和物理形式和概念有解释清楚了,那么,为什么会正交呢?
各种模态分析方法总结与比较 一、模态分析 模态分析是计算或试验分析固有频率、阻尼比和模态振型这些模态参数的过程。 模态分析的理论经典定义:将线性定常系统振动微分方程组中的物理坐标变换为模态坐标,使方程组解耦,成为一组以模态坐标及模态参数描述的独立方程,以便求出系统的模态参数。坐标变换的变换矩阵为模态矩阵,其每列为模态振型。 模态分析是研究结构动力特性一种近代方法,是系统辨别方法在工程振动领域中的应用。模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。这个分析过程如果是由有限元计算的方法取得的,则称为计算模记分析;如果通过试验将采集的系统输入与输出信号经过参数识别获得模态参数,称为试验模态分析。通常,模态分析都是指试验模态分析。振动模态是弹性结构的固有的、整体的特性。如果通过 AHA12GAGGAGAGGAFFFFAFAF
模态分析方法搞清楚了结构物在某一易受影响的频率范围内各阶主要模态的特性,就可能预言结构在此频段内在外部或内部各种振源作用下实际振动响应。因此,模态分析是结构动态设计及设备的故障诊断的重要方法。 模态分析最终目标是在识别出系统的模态参数,为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。 AHA12GAGGAGAGGAFFFFAFAF
AHA12GAGGAGAGGAFFFFAFAF 二、各模态分析方法的总结 (一)单自由度法 一般来说,一个系统的动态响应是它的若干阶模态振型的叠加。但是如果假定在给定的频带内只有一个模态是重要的,那么该模态的参数可以单独确定。以这个假定为根据的模态参数识别方法叫做单自由度(SDOF)法n1。在给定的频带范围内,结构的动态特性的时域表达表示近似为: ()[]}{}{T R R t r Q e t h r ψψλ= 2-1 而频域表示则近似为: ()[]}}{ {()[]2ωλωψψωLR UR j Q j h r t r r r -+-= 2-2 单自由度系统是一种很快速的方法,几乎不需要什么计算时间和计算机内存。 这种单自由度的假定只有当系统的各阶模态能够很好解耦时才是正确的。然而实际情况通常并不是这样的,所以就需要用包含若干模态的模型对测得的数据进行近似,同时识别这些参数的模态,就是所谓的多自由度(MDOF)法。 单自由度算法运算速度很快,几乎不需要什么计算和计
实验五 悬臂梁各阶固有频率及主振形的测定试验 一、实验目的 1、用共振法确定悬臂梁横向振动时的各阶固有频率。 2、熟悉和了解悬臂梁振动的规律和特点。 3、观察和测试悬臂梁振动的各阶主振型。分析各阶固有频率及其主振型的实测值与理论计算值的误差。 二、基本原理 悬臂梁的振动属于连续弹性体的振动,它具有无限多自由度及其相应的固有频率和主振型,其振动可表示为无穷多个主振型的叠加。对于梁体振动时,仅考虑弯曲引起的变形,而不计剪切引起的变形及其转动惯量的影响,这种力学分析模型称为欧拉-伯努利梁。 运用分离变量法,结合悬臂梁一端固定一端自由的边界条件,通过分析可求得均质、等截面悬臂梁的频率方程 1 L Lch cos -=ββ (5-1) 式中:L ——悬臂梁的长度。 梁各阶固有园频率为 A EI i i n 2 ρβω= (5-2) 对应i 阶固有频率的主振型函数为 ) ,3,2,1() sin (sin cos cos )( =-++- -=i x x sh L L sh L L ch x x ch x X i i i i i i i i i ββββββββ (5-3) 对于(5-1)式中的β,不能用解析法求解,用数值计算方法求得的一阶至四阶固有园频率和主振型的结果列于表5-1。 各阶固有园频率之比 1f ﹕1f ﹕1f ﹕1f ﹕… = 1﹕6.269﹕17.56﹕34.41﹕… (5-4) y A B x h L b 图5-1 悬臂梁振动模型 表(5-1)给出了悬臂梁自由振动时i =1~4阶固有园频率及其相应主振型函数。除了悬臂梁固定端点边界位移始终为零外,对于二阶以上主振型而言,梁上还存在一些点在振动过程中位移始终为零的振型节点。i 阶振型节点个数等于i -1,即振型节点个数比其振型的阶数小1。 实验测试对象为矩形截面悬臂梁(见图5-2所示)。在实验测试时,给梁体施加一个大小适当的激扰作用力,其频率正好等于梁体的某阶固有频率,则梁体便会产生共振,这时梁体变形即为该阶固有频率所对应的主振型,其它各阶振型的影响很小可忽略不计。用共振法确定悬臂梁的各阶固有频率及振型,我们只要连续调节激扰力,当悬臂梁出现某阶主振型且振动幅值最大即悬臂梁产生共振时,这时激扰力的频率就可以认为是悬臂梁的这一阶振动的固有频率。在工程实践中,最重要是确定振动系统最低的几阶固有频率及其主振型。本实验主要运用共振法测定悬臂梁一、二、三、四阶固有频率及其相应的主振型。
4.2 多自由度系统的固有频率与主振型 一、固有频率和主振型 上节导出了多自由度系统的自由振动微分方程: 以及 考虑到系统的主振动是简谐振动,可设它为: (4-10) 将它分别代入(4-5)与(4-7)式,可得如下主振型方程 (4-11)以及 (4-12)如果引入系统矩阵的概念,可以将式(4-11)与(4-12)化成具有相同的形式,对(4-11)式两端乘以,可得 (4-13)这时,设系统矩阵为 (4-14)且令,则主振型方程(4-11)可化为 (4-15) 再设另一个形式的系统矩阵为 (4-16)且令,则主振型方程(4-12)可化为 (4-17)这样,主振型方程(4-15)与(4-17)就有着相同的形式。 注意到系统的刚度矩阵与柔度矩阵之间存在着互逆关系,即有
或 利用矩阵乘积的求逆公式,可知上述两种系统矩阵之间有着互逆关系: 还应该指出,尽管系统的刚度矩阵、柔度矩阵以及质量矩阵一般都是对称矩阵,但是其系统矩阵和一般已不再是对称矩阵。 现在来看系统固有频率与主振型问题。鉴于方程(4-15)与(4-17)属于同一形式,故只需讨论其中之一。 方程(4-15)可改写为 (4-18) 它有非零解的条件为 (4-19) (4-19)式称为系统的频率方程或特征方程。对它展开的结果,可得一个关于的次代数方程: (4-20) 它的个根成为系统的特征根,亦称矩阵的特征值。特征值与系统固有频率之间有如下关系: (4-21) 一般说来,次代数方程的个根,可以是单根,也可以是重根;可以是实数,也可以是复数。但是,在我们所考虑的情形中,由于系统质量矩阵是正定的实对称阵,刚度矩阵是正定的或半正定的,故所有特征值都是实数,并且是正数或零。事实上,由正定与半正定的条件,对于任何非零的,有 (4-22) 现对系统主振型方程 两端前乘以,得 考虑到条件式(4-22),自然就得出上述结论。 通常,刚度矩阵为正定(或半正定)的系统,称为正定系统(或半正定系统)。所以,上述结论可改述为:正定系统的特征值都是正的,而半正定系统的特征值是正数或零。
实验二十八悬臂梁固有频率测量实验 1. 简介 悬臂梁实验台主要是针对高校工程测试课程实验教学需要而设计的,结合drvi快速可重组虚拟仪器开发平台、振动测量传感器和数据采集仪,可以开设悬臂梁固有频率测量实验。 2. 结构组成 悬臂梁实验台的结构示意如图1所示,结构总体尺寸为120×110×150mm(长×宽×高),主要包括的零件有: 图1 悬臂梁实验台结构示意图 1. 悬臂 2. 底座 3. 操作说明 3.1 实验准备 运用悬臂梁实验台进行实验教学所需准备的实验设备为: 1. 悬臂梁实验台(lxbl-a)1套 2. 加速度传感器(yd-37)1套 3. 加速度传感器变送器(lbs-12-a)1台 4. 蓝津数据采集仪(ldaq-epp2)1台 5. 开关电源(ldy-a)1套 6. 脉冲锤1只 7. 5芯对等线1条 备齐所需的设备后,将加速度传感器安装在悬臂梁前端的安装孔上,然后将加速度传感器与变送器相连,变送器通过5芯对等线与数据采集仪1通道连接,数据采集仪通过并口电缆与pc机并口连接,加速度传感器调理电路模块接线如图2所示。在保证接线无误的情况下,可以开始进行实验。
图2 加速度传感器调理电路接线示意图 3.2 实验操作 悬臂梁固有频率测量实验利用加速度传感器来测量悬臂振动的信号,经过频谱变换(fft)处理后得到悬臂梁的一阶固有频率,需要注意的是该实验数据采集采用预触发方式,数据采集仪的触发电平要根据现场情况进行设置,实验过程如下: 1. 启动服务器,运行drvi主程序,开启drvi数据采集仪电源,然后点击drvi快捷工具条上的“联机注册”图标,进行服务器和数据采集仪之间的注册。联机注册成功后,启动drvi内置的“web服务器功能”,开始监听8500端口。 图3 悬臂梁固有频率测量实验样本图 2. 启动drvi中的“悬臂梁固有频率测量”实验脚本,然后设定数据采集仪的工作模式为外触发采样,同时设置触发电平(如800)和预触发点数(如20),然后点击“运行”按钮启动采样过程(由于采用外触发采样方式,此时处于等待状态)。 3. 用脉冲锤敲击悬臂梁,产生脉冲激振。敲击的力幅要适当,着力点要准确,迅速脱开。如检测不到冲击振动信号,则适当修改采集仪中的预触发电平,然后点击面板中的“开始”按钮再次进行测量,此时,信号分析窗口中应显示出悬臂梁受瞬态激励后输出的信
模态分析中的几个基本概念 一、模态定义:物体按照某一阶固有频率振动时,物体上各个点偏离平衡位置的位移是满足一定的比例关系的,可以用一个向量表示。 模态分析一般是在振动领域应用,每个物体都具有自己的固有频率,在外力的激励作用下,物体会表现出不同的振动特性: 一阶模态是外力的激励频率与物体固有频率相等的时候出现的,此时物体的振动形态叫做一阶振型或主振型; 二阶模态是外力的激励频率是物体固有频率的两倍时候出现,此时的振动外形叫做二阶振型,以依次类推。 一般来讲,外界激励的频率非常复杂,物体在这种复杂的外界激励下的振动反应是各阶振型的复合。 二、模态分析:模态是结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。 有限元中模态分析的本质是求矩阵的特征值问题,所以“阶数”就是指特征值的个数。将特征值从小到大排列就是阶次。 实际的分析对象是无限维的,所以其模态具有无穷阶。但是对于运动起主导作用的只是前面的几阶模态,所以计算时根据需要计算前几阶的。 一个物体有很多个固有振动频率(理论上无穷多个),按照从小到大顺序,第一个就叫第一阶固有频率,依次类推。所以模态的阶数就是对应的固有频率的阶数。 三、振型是指体系的一种固有的特性。它与固有频率相对应,即为对应固有频率体系自身振动的形态。每一阶固有频率都对应一种振型。振型与体系实际的振动形态不一定相同。振型对应于频率而言,一个固有频率对应于一个振型。按照频率从低到高的排列,来说第一振型,第二振型等等。此处的振型就是指在该固有频率下结构的振动形态,频率越高则振动周期越小。在实验中,我们就是通过用一定的频率对结构进行激振,观测相应点的位移状况,当观测点的位移达到最大时,此时频率即为固有频率。实际结构的振动形态并不是一个规则的形状,而是各阶振型相叠加的结果。 四、模态扩展是为了是结果在后处理器中观察而设置的,原因如下: 求解器的输出内容主要是固有频率,固有频率被写到输出文件Jobname.OUT及振型文件Jobnmae.MODE中,输出内容中也可以包含缩减
悬臂梁固有频率测量
上海第二工业大学 名称:传感器与测试技术技能实习 专业:机械电子工程 班级:13机工A1 姓名: 学号:2013481 指导老师:杨淑珍孙芳方 实训地点:14#407
目录 一、技能实习内容及要求 (1) 二、总体方案设计 (2) 2-1. 测量原理 (2) 2-2. 测试系统组成 (2) 2-3. 激励方法 (3) 三、实验硬的件选用 (3) 3-1、悬臂梁 (3) 3-2.传感器 (4) 3-3、电荷放大器 (5) 3-4、采集卡 (6) 四、硬件电路的设计 (6) 五、测量软件设计 (9) 六、小结和体会 (16)
一、技能实习内容及要求 1-1. 内容: 设计一个测试悬臂梁固有频率的自动测试系统,悬臂梁如下所示: 具体技术要求: 能显示相应所采集到的波形图、频谱图等相关图 能显示固有频率 能对固有频率进行超限报警,上下限制用户可设定 生成当前测试报告,(包括相应波形图和固有频率值以及合格状态) 1-2. 实训要求: 1、提出设计方案(提出测量原理,传感器选用和安装,构建测试系统) 2、设计测量电路(包括放大,滤波电路,制作滤波电路) 3、测试软件设计:利用Labview或其它开发程序(VB、VC等),设计测量软件进行数据采集和分析 4、调试 5、撰写实训报告 1-3. 报告要求: 1.实训内容 2.撰写总体设计方案 3.硬件选用(包括传感器、采集卡的选用和安装等) 4.电路设计(包括测量电路设计,系统总电路)
5.测量软件设计(包括软件设计流程图,各功能实现方法和代码,包括个主程序,子程序描述以及相应的重要参数设置如采样通道,采样频率,采样点数) 6.小结和体会(可包含调试中遇到的问题) 二、总体设计方案 2-1.测量原理: 在测试的过程中,通过脉冲锤敲击悬臂梁的横梁产生一个脉冲信号。信号会逐渐衰减,在衰减过程中会有一个时刻衰减到的频率和悬臂梁的固有频率相同,我们要找到的就是这个相同的频率,这个频率与悬臂梁固有频率形成共振,那时候的复制达到最大,用labview分析这个值,就可以测出悬臂梁的固有频率。 2-2.测试系统的组成: 图1测试系 测试系统包括下述三个主要部分: 激励部分:
悬臂梁固有频率的计 算
悬臂梁固有频率的计算 试求在0x =处固定、x l =处自由的等截面悬臂梁振动的固有频率(求解前五阶)。 解:法一:欧拉-伯努利梁理论 悬臂梁的运动微分方程为:4242(,)(,)+0w x t w x t EI A x t ρ??=??; 悬臂梁的边界条件为:2222(0)0(1),(0)0(2)0(3),(EI )0(4)x l x l dw w w w x x dx x x x ==???======???,; 该偏微分方程的自由振动解为(x,t)W(x)T(t)w =,将此解带入悬臂梁的运动微分方程可得到1234(x)C cos sin cosh sinh W x C x C x C x ββββ=+++,(t)Acos t Bsin t T w w =+;其中2 4A EI ρωβ= 将边界条件(1)、(2)带入上式可得13C 0C +=,24C 0C +=;进一步整理可得12(x)C (cos cosh )(sin sinh )W x x C x x ββββ=-+-;再将边界条件(3)、(4)带入可得12(cos cosh )C (sin sinh )0C l l l l ββββ-+-+=;12(sin sinh )C (cos cosh )0C l l l l ββββ--+-+=要求12C C 和有非零解,则它们的系数行列式必为零,即 (cos cosh ) (sin sinh )=0(sin sinh )(cos cosh ) l l l l l l l l ββββββββ-+-+--+-+ 所以得到频率方程为:cos()cosh()1n n l l ββ=-;该方程的根 n l β表示振动系统的固有频率:1224 ()(),1,2,...n n EI w l n Al βρ==满足上式中的各n l β(1,2,...n =)的值在书P443表8.4中给出,现罗列如下:123451.875104 4.6940917.85475710.99554114.1372l l l l l βββββ=====,,,,;