简支梁固有频率及振型函数

简支梁自由振动加速度时间历程曲线一、简支梁自由振动的基本概念简支梁是一种常见的结构形式，其自由振动是指在没有外力作用下，梁体在初始位移或初速度的情况下，按照固有频率进行振动。

简支梁自由振动加速度时间历程曲线可以反映出简支梁的振动特性。

二、简支梁自由振动的计算方法1. 求解固有频率固有频率是指在没有外力作用下，结构体系按照某种方式进行自由振荡时的频率。

对于简支梁来说，其固有频率公式为：f = 1/2π * √(E*I/(m*L^3))其中，E为弹性模量，I为截面惯性矩，m为单位长度质量，L为梁长。

2. 求解振型函数振型函数描述了结构体系在某个特定频率下的运动状态。

对于简支梁来说，其一阶弯曲模态（最常见的模态）的振型函数为：y(x,t) = A*sin(ωt)sin(kx)其中，A为幅值，ω为角频率（等于2πf），k为波数（等于2π/λ），λ为波长。

3. 求解振动加速度振动加速度是指结构体系在某个时刻的加速度大小，可以通过对振型函数进行二阶导数求解。

对于简支梁来说，其一阶弯曲模态的振动加速度公式为：a(x,t) = -ω^2 A*sin(ωt)sin(kx)三、简支梁自由振动加速度时间历程曲线的绘制方法1. 确定梁长、截面形状和材料参数在绘制简支梁自由振动加速度时间历程曲线之前，需要确定梁长、截面形状和材料参数。

这些参数将直接影响到固有频率和振型函数的计算结果。

2. 计算固有频率和振型函数根据上述公式，可以计算出简支梁的固有频率和一阶弯曲模态的振型函数。

其中，固有频率可以通过改变材料参数、截面形状或梁长等方式进行调整。

3. 绘制加速度时间历程曲线将一阶弯曲模态的振型函数带入到上述公式中，即可得到任意时刻任意位置处的振动加速度大小。

将这些数据按照时间顺序绘制成曲线，即可得到简支梁自由振动加速度时间历程曲线。

四、简支梁自由振动加速度时间历程曲线的分析通过观察简支梁自由振动加速度时间历程曲线，可以得到以下结论：1. 振动加速度大小随时间呈正弦变化，其周期等于固有周期。

简支梁横向振动的固有频率及振型函数的推导一．等截面细直梁的横向振动取梁未变形是的轴线方向为X 轴（向右为正），取对称面内与x 轴垂直的方向为y 轴（向上为正）。

梁在横向振动时，其挠曲线随时间而变化，可表示为y=y(x,t) (1)除了理想弹性体与微幅振动的假设外，我们还假设梁的长度与截面高度之比是相当大的（大于10）。

故可以采用材料力学中的梁弯曲的简化理论。

根据这一理论，在我们采用的坐标系中，梁挠曲线的微分方程可以表示为：22yEI M x ∂=∂(2) 其中，E 是弹性模量，I 是截面惯性矩，EI 为梁的弯曲刚度，M 代表x 截面处的弯矩。

挂怒弯矩的正负，规定为左截面上顺时针方向为正，右截面逆时针方向为正。

关于剪力Q 的正负，规定为左截面向上为正，右截面向下为正。

至于分布载荷集度q 的正向则规定与y 轴相同。

在这些规定下，有：M QQ q x x ∂∂==∂∂， (3)于是，对方程（2）求偏导，可得：222222(EI )(EI )y M y Q Q q xx x x x x ∂∂∂∂∂∂====∂∂∂∂∂∂，(4)考虑到等截面细直梁的EI 是常量，就有：3434y yEI Q EI q x x ∂∂==∂∂，(5)方程（5）就是在等截面梁在集度为q 的分部李作用下的挠曲微分方程。

应用达朗贝尔原理，在梁上加以分布得惯性力，其集度为22y q t ρ∂=-∂(6)其中ρ代表梁单位长度的质量。

假设阻尼的影响可以忽略不计，那么梁在自由振动中的载荷就仅仅是分布的惯性力。

将式（6）代入（5），即得到等截面梁自由弯曲振动微分方程：4242y yEI x t ρ∂∂=--∂∂ (7)其中2/a EI ρ=。

为求解上述偏微分方程（7），采用分离变量法。

假设方程的解为：y(x,t)=X(x)Y(t)(8)将式（8）代入（7），得：224241Y a d XY t X dx ∂=-∂ (9) 上式左端仅依赖于t,而右端仅依赖于x ，因此要使对于任何x,t 上式均成立，必须二者均等于一个常数。

《振动测试实验》实验报告∗南京航空航天大学机械结构力学及控制国家重点实验室二○一一年∗注：实验报告完成后请以附件形式发送至：wt78@邮件主题请写明：《振动测试实验报告》，姓名，学号，分班号（三班或四班）一、实验目的•测量双简支梁的固有频率和振型。

•理解多自由度系统振型的物理概念。

•掌握多自由度系统固有频率和振型的简单测量方法。

二、实验原理图简支梁固有频率和振型测试原理图三、实验过程1、将功率放大器“输出调节”旋至最小，“信号选择”置“外接”。

打开各设备电源。

2、进入“双简支梁固有频率与振型测量”实验操作界面，使信号发生器的输出频率约为 30Hz，输出电压约为 1V 。

调节功率放的“输出调节”，逐渐增大其输出功率直至质量块有明显的振动（观察并用手触摸）。

3、将信号发生器输出频率由低向高逐步调节，同时观察李萨育图形。

当李萨育图为稳定的正椭圆时，信号发生器的频率读数即为第一阶固有频率。

继续将信号发生器的频率向高逐步调节，测出第二阶、第三阶固有频率。

4、再将信号发生器调到第一阶固有频率值，保持功率放大器的输出功率恒定（即：不再改变信号发生器的输出电压和功率放大器的输出功率），保持“参考”传感器的位置不变。

将“测量”传感器从双简支梁的右端等距跑点，依次记下“测量”传感器在各个位置时的测量点与参考点传感器输出电压之比（即“测量点/参考点”的显示值）及其正负号。

将其归一化即可得到第一阶振型，填“振型数据”表格。

点击“振型图”或“振型动画”检验振型数据。

四、实验数据与分析1、列出固有频率。

双简支梁的3个阶段的固有频率分别为：一阶： 36.7Hz二阶： 136.5Hz三阶： 326.6Hz一阶振型图二阶振型图3、测量双简单支梁振型时，改变“测量”传感器位置后，李萨育图形出现非正椭圆，解释原因，如何避免？答：测量双简单支梁振型时，改变“测量”传感器位置后，由于传感器有一定的质量，改变传感器位置也就改变了系统的质量分布，必然引起其固有频率的变化，在李萨育图形上表现出呈非正椭圆。

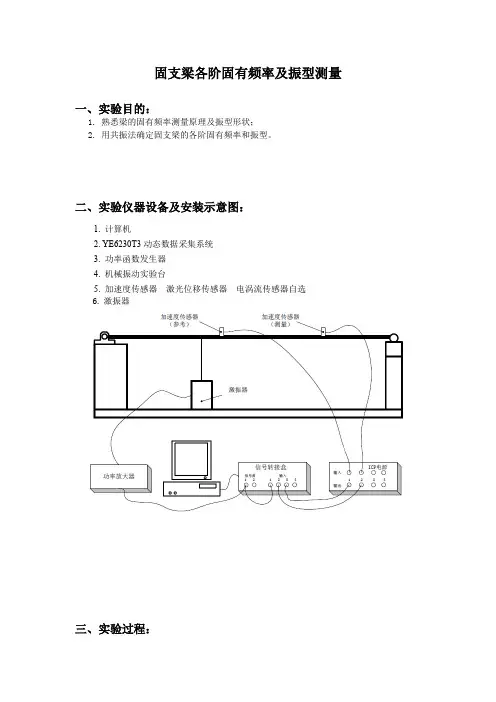
固支梁各阶固有频率及振型测量
一、实验目的：
1. 熟悉梁的固有频率测量原理及振型形状；
2. 用共振法确定固支梁的各阶固有频率和振型。

二、实验仪器设备及安装示意图：
1. 计算机
2. YE6230T3动态数据采集系统
3. 功率函数发生器
4. 机械振动实验台
5. 加速度传感器激光位移传感器电涡流传感器自选
6. 激振器
三、实验过程：
四、实验结果及分析：
1、前三阶固有频率测量结果
2、各测点实测振幅（单位：）1，175；
3、各测点振幅换算值
4、绘出固支梁前三阶振型图一阶振型图
二阶振型图三阶振型图
多自由度系统各阶固有频率及主振型的测量一、实验目的
二、实验设备及安装示意图
三、实验结果与分析
1、不同张力下各阶固有频率的理论计算值与实测值
2、绘出观察到的三自由度系统振型曲线。

3、将理论计算出的各阶固有频率、理论振型与实测固有频率、实测振型相比较，是否一致? 产生误差的原因在哪里?。

简支梁振动模态分析与频率响应优化简支梁是一种常见的结构形式，广泛应用于桥梁、楼板等工程领域。

对于简支梁的振动模态分析与频率响应优化，具有重要的工程价值和理论意义。

本文将从理论分析和实际工程角度出发，探讨简支梁振动模态分析的方法以及频率响应优化的实践。

首先，简支梁振动模态分析的方法显得尤为重要。

振动模态是指结构在自由振动过程中的振动形态和频率分布。

对于简支梁而言，振动模态的分析可以帮助工程师了解结构的振动特性，从而为结构设计和改进提供指导。

一般而言，简支梁的振动模态分析可以通过数学模型和有限元分析两种常见方法实现。

数学模型方法主要通过数学方程和边界条件推导结构的振动模态。

以简支梁为例，可以利用波动方程等偏微分方程来描述梁的振动过程。

然后，通过求解这些方程，可以得到梁的振动模态和频率。

这种方法具有计算量小、理论基础强等优点，适合用于简单的梁结构。

然而，数学模型方法常常忽略了结构的复杂性，无法准确描述实际工程中的各种边界条件和材料非线性等因素。

有限元分析方法是近年来发展起来的一种结构振动分析方法，能够更好地模拟实际工程中的各种复杂条件。

该方法将结构离散成许多小元素，然后通过有限元法计算结构的振动模态。

对于简支梁而言，可以将整个梁划分成多个小单元，然后求解结构的特征值和特征向量。

通过有限元分析，可以全面考虑结构的几何形状、材料力学性能、边界条件等因素，准确预测简支梁的振动模态。

然而，有限元分析的计算量较大，且需要对模型进行合理的离散化处理，对于复杂的简支梁结构，仍然存在一定的挑战。

简支梁振动模态分析的结果对于结构的优化设计和改进具有指导意义。

通过分析振动模态，工程师可以了解结构的固有频率和振动形态，从而可以评估结构的稳定性和安全性。

在实际工程中，如果简支梁的某一振动模态频率接近材料的固有频率，那么就需要调整结构的几何形状或者材料性能，以避免共振的产生。

此外，振动模态分析还可以用于判断结构的缺陷和损伤，通过观察特定模态的变化，可以识别出可能存在的结构问题。