基于MATLAB的机器人正运动学分析与仿真

六自由度机械臂运动学分析与仿真研究肖俊明;韩伟;王瑷珲;李继朋;梁旺【摘要】运用D-H参数法确定机械臂的参数、坐标系,建立机械臂的运动学方程.在Matlab软件中进行数值计算,通过分析机械臂的工作空间,得到了机械臂工作空间图.在Matlab工作环境下,用机器人工具箱Robotics Toolbox对所建六自由度机械臂运动学模型的正运动学、逆运动学、轨迹规划进行验证与仿真,得到了各关节的角位移、角速度、角加速度与时间的关系曲线.研究表明,该机械臂运动空间设计直观、精确,为机械臂控制系统设计、动力学分析及轨迹规划提供了理论基础和参考依据.【期刊名称】《中原工学院学报》【年(卷),期】2018(029)004【总页数】7页(P77-83)【关键词】机械臂;六自由度;运动学;仿真【作者】肖俊明;韩伟;王瑷珲;李继朋;梁旺【作者单位】中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007;中原工学院电子信息学院,河南郑州450007【正文语种】中文【中图分类】TP24220世纪60年代初机器人问世以来，机器人技术逐步取得了实质性的进步与成果[1]，目前已被应用于很多行业，在航空航天、汽车工业、海洋探索、医疗手术等行业的高科技领域发挥着重要作用，促进了人们生活的改善。

机械臂是最早应用于实际生产领域的一种机器人[2]。

其中，串联机械臂应用最为广泛，它是由若干通过关节连接在一起的连杆组成的具有多个自由度的开链型连杆机构。

它的一端固定在基座上，另一端为末端执行器，主要进行抓取操作，中间部分是由若干带驱动的转动或移动关节串联而成的机构体。

机械臂运动学研究的是各连杆关节的运动与机械臂各部分(一般为末端执行器)的位置、姿态之间的数学关系。

研究这种关系是设计机械臂运动控制器所必需的。

机械臂运动学的研究主要有正运动学问题和逆运动学问题两类。

基于MATLAB的六自由度机械臂运动仿真分析
王春荣;夏尔冬
【期刊名称】《榆林学院学报》
【年(卷),期】2017(027)002
【摘要】以某六自由度机械臂为研究对象,利用PRO/E建立其三维建模.分析了机械臂的D-H坐标参数、运动学以及雅克比矩阵,借助MATLAB软件构建机械臂模型.仿真分析机械臂在直角坐标系与关节坐标系下的轨迹规划.仿真实验表明,机械臂手部末端的运动轨迹平稳且没有跳跃点,并且在插补过程中,每个关节的角位移,角速度和角加速度的变化十分连贯、匀速没有任何跳跃点,该机械臂设计合理.
【总页数】5页(P11-14,25)
【作者】王春荣;夏尔冬
【作者单位】三明学院机电工程学院,福建三明365004;三明学院机电工程学院,福建三明365004
【正文语种】中文
【中图分类】TP242
【相关文献】
1.基于MATLAB和ADAMS的六自由度并联运动机床运动学仿真 [J], 李滨城;杨丹;顾金凤
2.基于 MATLAB／Robotics Toolbox的六自由度机械臂仿真 [J], 王彦璋
3.六自由度机械臂运动学及奇异性仿真分析 [J], 袁媛
4.基于放疗的六自由度医用机械臂动力学仿真分析 [J], 陈继朋;陈惠贤;杨小龙;刘
晓娟;乔宇;马利强
5.六自由度机械臂的运动学分析与Matlab仿真 [J], 夏亚飞;魏国春;吝健全;夏楠因版权原因，仅展示原文概要，查看原文内容请购买。

. -计算机辅助设计报告三轮全向移动机器人运动控制仿真202103009004 余广202103009019202103009031 斌人员分工：余广：总体负责，系统理解及控制器设计，PPT制作，后期报告审查及修改斌：PPT制作，报告撰写：资料收集，辅助其余两人完成任务目录一、实验目的3二、实验原理32.1控制对象——三轮全向机器人32.2 控制系统构造4三、实验容53.1电机模型53.1.1物理建模53.1.2 Simulink模块搭建73.1.3无刷直流电机仿真模型的验证103.2运动学模型123.2.1物理建模123.2.2 Simulink模块搭建133.3 路径规划143.4. 传感器设计153.5.控制器设计163.5.1 电机控制器设计163.5.2 运动控制器设计183.6 观测器22四、结果验收234.1 x轴方向的误差244.2 y轴方向的误差244.3 前进方向偏角254.4 速度误差25五、致26六、附录〔路径规划函数〕26一、实验目的（一）建立三轮全向机器人系统的数学模型，然后基于simulink建立该系统的仿真模型并设计控制器，最终满足控制要求；（二）控制的最终目的是使该机器人能够良好跟踪预期的运动轨迹；（三）通过对复杂系统的分析、建模、仿真、验证，全面提高利用计算机对复杂系统进展辅助设计的能力；（四）通过集体作业、分工完成任务的方式培养团队意识，提高团队集体攻关能力二、实验原理2.1控制对象——三轮全向机器人三轮全向移动机器人其驱动轮由三个全向轮组成，径向对称安装，各轮互成120°角，滚柱垂直于各主轮。

三个全向轮的大小和质量完全一样，而且由性能一样的电机驱动。

图1 三轮全向移动机器人2.2 控制系统构造图2基于运动学模型的分层控制框图三、实验容3.1电机模型3.1.1物理建模瑞士的MAXON公司的无刷直流电机建模如下:无刷直流电机的数学模型，其等效电路如下列图所示：根据上图，建立电机数学方程如下： ➢ 瞬态电压方程➢ 电压方程➢ 转矩方程000000a a ab a b ac c u i R u R i R u i ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦()111a a b nb c c di dt e di L M e u dt e di dt ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦1[()()]3n a b c a b c u u u u e e e =++-++a a b b c cem e i e i e i T ++=Ω➢ 运动方程3.1.2 Simulink 模块搭建根据以上数学模型，我们搭建电机的Simulink 模块如下：➢ 电压方程模块➢ 转矩方程模块em L T T B Jp --Ω=Ω➢运动方程模块➢其他必要模块设计反电动势模块逻辑换向模块➢模块组装——电机仿真模型➢驱动电机模块封装3.1.3无刷直流电机仿真模型的验证到此电机的建模就算完成了，但其正确性还需要结果来验证，以下是仿真结果：i.绕组端电压波形：ii.反电动势波形iii.电流波形iv.转速波形根据图像可知，仿真结果跟实际是相吻合的。

基于matlab的机器人工作空间求解方法机器人工作空间求解的基础是在一个多维空间中根据机器人臂的坐标、参数以及机器人的运动范围，利用数学等方法，找到机器人在给定范围内可实现执行任务的最优解。

一、基本概念：1、机器人工作空间：机器人工作空间指机器人多轴运动系统运动范围，是一个包括机器人参数、机器人操作范围、机器人运动路径等信息的高维空间，主要用于研究和分析机器人的运动学和动力学行为。

2、机器人运动学：机器人运动学主要研究机器人的坐标、参数以及运动范围，包括机器人位置及速度计算，运动路径规划，以及主轴等可控制的量的变化，这些工作需要对机器人参数进行精确建模和仿真，避免机器人工作空间中发生危险或无法完成任务的情况。

二、matlab工具及其原理：在机器人工作空间求解过程中，matlab软件包可以提供专业的解决方案，以实现机器人运动学计算、路径规划以及仿真等任务。

1、 matlab机器人工作空间求解主要分两步：三、matlab机器人工作空间求解的具体步骤：1、配置环境：确保安装matlab软件的环境即R14以上的版本，配置完成后运行matlab中的Robot;2、建立参数文件：建立参数文件是按照机器人运动参数和机器人参数建立相应的参数文件，使用matlab绘制参数曲线，并建立多个机器人支撑工作空间的视图；3、绘制工作空间：可以借助matlab的绘图工具对机器人的工作空间进行绘图，根据绘制的坐标和图形观察机器人的工作空间，采用matlab编程语言根据工作范围编写EOI求解算法；4、机器人求解：调用matlab命令，根据编写的程序和EOI求解算法，实现机器人工作空间的求解，根据求解出来的解决方案，对如何控制机器人采取最佳运动轨迹、最佳控制机器人的参数进行调整；5、机器人运行：最后，将求解出来的具体方案和机器人的参数设置，调用matlab的求解器运行在机器人中，实现最佳的机器人运动路径。

四、机器人工作空间求解的应用：1、机器人运动学计算：运用机器人工作空间求解可以确定和控制机器人的行走路线和速度，防止机器人发生碰撞，以达到间隔定位，做到准确规划机器人的移动轨迹；。

《装备制造技术》2021年第2期四自由度工业机器人运动学分析与仿真张洪波1,孟丹1,潘宜斌2,冯宝林1,岳亮亮1,李磊1 (1•常州先进制造技术研究所，江苏常州213164:2.合肥固泰自动化有限公司，合肥230051 )摘要：以高粉尘环境下四自由度工业机器人为研究对象，利用D-H法建立机器人运动学方程，求出其位置的解析解，利用solidworks软件建立机器人的三维虚拟样机，并用recurdyn软件进行了运动学仿真验证关键词：工业机器人;运动学分析；运动学仿真中图分类号：TP242.2 文献标识码:A 文章编号：1672-545X(2021 >02-0017-030引言随着人力成本的逐步提高，搬运码垛等运输工 业的发展遭遇了前所未有的掣肘，高速重载工业机 器人技术的研究已成为我国工业领域亟待解决的问 题。

当前，四自由度码垛机器人多是由两个旋转关节 和两个移动关节组成的混联机器人，而四个旋转关 节机器人具有动作灵活、工作空间大、干涉小、结构 紧凑、易密封防尘等优点l h21。

本文采用双平行四边形 串联机构,增加了机器人本体整体刚度，同时可以维 持末端执行机构的水平姿态；对四自由度工业机器 人的四个旋转关节进行结构分析和运动学分析，在 不考虑力与力矩情况下，将机器人相对于固定参考 坐标系的运动作为时间的函数，研究了关节变量和 机器人末端位姿的关系i3'并用recurdyn进行运动 学仿真，验证了机器人数值计算，同时为机器人后续 的轨迹规划,动力学性能分析提供参考。

1机器人结构设计本文机器人的设计负载250 kg，主要由四个旋 转关节组成：（1)转座通过轴线竖直的旋转关节与底 座相连；（2)转座为机器人本体的支撑机构，其上安 装有平衡缸、大臂和副杆连杆；（3)小臂通过电机、减 速器直驱方式安装在大臂关节处，旋转关节处亦为 副杆连杆支撑点；(4)腕部与小臂通过旋转关节相连, 通过副杆连杆和大、小臂形成的平行四边形机构，使 腕部始终保持水平，同时满足腕部的易控性,腕部结 构为法兰盘形式，根据执行机构的不同，连接特定的执行器|51。

基于MATLAB/Simulink的二连杆机器人的PID控制与仿真作者：***来源：《科技资讯》2019年第07期摘; 要：主要研究了一类二连杆机器人应用PID控制理论进行轨迹追踪的控制方法。

该文首先给出二连杆机器人进行动力学模型，进而利用MATLAB/Simulink仿真环境，构造出PID 控制模型框图，使用Interpreted MATLAB Function嵌入代码。

通过改变PID参数进行仿真，该文分析了不同PID参数对二连杆机器人关节转角误差的影响，使机器人末端实际轨迹实现了很好的跟踪效果。

关键词：二连杆机器人; Simulink; PID控制中图分类号：G64; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 文献标识码：A; ; ; ; ; ; ; ; ; ; ; ; ; 文章编号：1672-3791（2019）03（a）-0030-02二连杆机器人是可自由改变关节转角而完成不同作业的装置，对二连杆机器人的关节转角的准确控制关乎产品的质量和生产的效率，是工业生产关键的一环，因此应用PID控制算法对其转角的控制显得尤为重要。

为减小二连杆机器人转角误差，于具有数值计算分析与数学建模功能的MATLAB/Simulink环境中应用PID控制理论模拟控制的全过程。

该文主要研究PID参数对二连杆机器人关节转角误差的影响，应用MATLAB中精确的矩阵等的运算和清晰的绘图功能，Simulink中简洁的模块联系和动态仿真曲线，得到了不同PID 参数下的误差曲线。

该文依托PID控制理论，以二连杆机器人运动轨迹为研究对象，通过MATLAB编程和Simulink仿真，构造出合理的理论模型，通过分析得到不同PID參数对误差的影响，进而能够使二连杆机器人运动轨迹基本与期望值相同，转角误差降至最低，达到了控制的目的。

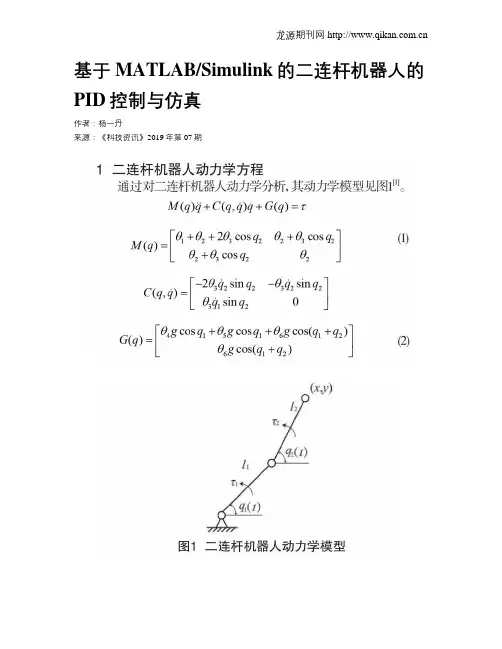
1; 二连杆机器人动力学方程通过对二连杆机器人动力学分析，其动力学模型见图1[1]。

第18卷第7期系统仿真学报©V ol. 18 No. 7 2006年7月Journal of System Simulation July, 2006基于MATLAB/Simulink机器人鲁棒自适应控制系统仿真研究高道祥，薛定宇（东北大学教育部暨辽宁省流程工业综合自动化重点实验室，沈阳 110004）摘要：介绍了一种在MATLAB/Simulink环境下进行机器人鲁棒自适应控制系统仿真的方法，利用Matlab软件强大的数值运算功能，将系统模型用Matlab语言编写成M-Function（或S-Function）文件，通过User-Defined-Function模块嵌入到Simulink仿真环境中，可以充分发挥Simulink模块实时的动态仿真功能，简化仿真模型的设计，修改和调整。

基于M-Function建立机器人系统模型的方法可以推广到其他复杂控制系统的建模，SimMechanics在建立多自由度连杆机器人受控对象仿真模型时，简单可靠。

关键词：机器人；Matlab/Simulink；SimMechanics；仿真；鲁棒自适应控制中图分类号：TP391.9 文献标识码：A 文章编号：1004-731X(2006) 07-2022-04Simulation Research of Robust Adaptive Control Systemfor Robotic Manipulators Based on MATLAB/SimulinkGAO Dao-xiang, XUE Ding-yü(Key Laboratory of Process Industry Automation, Ministry of Education, Northeast University, Shenyang 110004, China) Abstract: A simulation method of robust adaptive control was proposed for the robotic manipulator system. The method took the advantage of the powerful computing function of Matlab to programme M-function (or S-Function) for the system model by Matlab language and embedded it to the Simulink by User-Defined-Function module. The real time dynamic simulating function of Simulink would be exerted adequately and the design, modification and adjust of the system model could be greatly simplified. The method of constructing manipulator control system model based on M-Function could be generalized to the other complicated control system and SimMechanics would make the n-links manipulator model conveniently and credibly.Key words: robotic manipulator; Matlab/Simulink; SimMechanics; simulation; robust adaptive control引言一个新的控制算法在付诸使用之前，无论从经济原因还是技术角度，都需要经过仿真阶段来测试控制系统的性能和缺陷。

基于MATLAB的机械系统动力学建模与分析随着科技的不断发展，机械系统的动力学建模与分析在工程领域中变得越来越重要。

在这个过程中，MATLAB作为一种强大的数值计算软件工具，被广泛应用于机械动力学的建模与分析中。

一、MATLAB在机械系统动力学建模中的应用机械系统的动力学建模需要建立一些力学方程，用于描述系统的运动和力学行为。

MATLAB提供了丰富的数值计算和符号计算功能，可以方便地进行动力学方程的建立和求解。

通过MATLAB中的数值分析工具和符号计算工具，可以将机械系统的动力学问题转化为一些数学方程，并利用MATLAB进行求解和分析。

二、机械系统动力学建模的实例以机械摆锤系统为例，介绍MATLAB在机械系统动力学建模与分析中的应用。

摆锤系统是一个经典的振动系统，由摆锤、绳索和支撑点组成。

将摆锤的位置表示为角度，可以利用运动学方程和动力学方程描述系统的运动和力学行为。

1. 运动学建模首先，建立机械摆锤系统的运动学模型。

利用MATLAB中的符号计算工具，可以建立摆锤的角度与时间的关系。

运动学方程可以通过角度关于时间的导数来表示，利用MATLAB中的符号计算工具求解微分方程，得到摆锤角度与时间的关系。

2. 动力学建模其次，建立机械摆锤系统的动力学模型。

利用牛顿第二定律和力矩平衡原理，可以建立摆锤的动力学方程。

通过MATLAB中的数值计算工具，可以利用微分方程求解工具求解动力学方程，得到摆锤的角加速度与时间的关系。

3. 动力学分析最后，利用MATLAB进行机械摆锤系统的动力学分析。

通过数值计算和绘图工具，可以分析系统在不同参数下的动力学行为。

例如，可以研究摆锤的运动轨迹、运动周期和运动幅度等。

利用MATLAB中的数值计算和绘图功能，可以直观地展示系统的动力学性能。

三、MATLAB在机械系统动力学分析中的优势MATLAB作为一种强大的数值计算软件工具，在机械系统动力学分析中具有许多优势。

1. 灵活性MATLAB提供了丰富的数值计算和符号计算功能，可以方便地进行动力学方程的建立和求解。

机器人灵巧手的运动学分析及仿真靳果;韩星;韩枫【摘要】为了实现对灵巧手各关节的实时控制，提高灵巧手工作的"灵巧度"，本文以英国Shadow公司的Shadow仿人灵巧手为研究对象，研究了Shadow灵巧手机械结构特点，运用D-H坐标法，建立了灵巧手的运动学模型，推导出灵巧手的单指正、逆运动学方程，求解出正、逆解析解及相关参数，并且运用Matlab软件对结果进行了验证和仿真，为进一步研究灵巧手动力学问题提供理论依据。

%In order to realize the real-time control of each joint of the dexterous hand and improve the"dexterity"during the working process, the mechanical structure characteristics of dexterous hand were studied and the research was based on Shadow dexterous hand. Then the kinematics model is established by using D-H parameter method , and the forward and inverse kinematics equations are derived. The analytical solution and related parameters were solved also. Finally the results are verified and simulated in Matlab. .The results are the theoretical reference for the further study of the dynamics of dexterous hand.【期刊名称】《电子设计工程》【年(卷),期】2015(000)001【总页数】4页(P119-122)【关键词】机器人灵巧手;运动学;Matlab;仿真【作者】靳果;韩星;韩枫【作者单位】河南工业职业技术学院河南南阳 473000;华北水利水电大学河南郑州 450045;中国人民解放军65555部队辽宁海城 114200【正文语种】中文【中图分类】TN609目前市场上出现的按摩设备多是起到放松、缓解疲劳的作用，对治疗疾病效果并不明显，因此，利用机器人技术研制出具有专业中医按摩水平的机器人灵巧手具有广阔的市场前景。

一、概述机械臂是一种自动化控制系统中常见的装置，它能够模拟人手的动作，广泛应用于工业生产线、医疗设备、航天航空等领域。

机械臂的运动学逆解是对机械臂的运动学方程进行反向求解，以求得机械臂在给定位置下的关节角度。

本文将针对七自由度机械臂的运动学逆解问题进行深入探讨，使用MATLAB进行数值计算和仿真。

二、机械臂的七自由度机械臂的自由度指的是它的可运动关节数量。

七自由度机械臂意味着它有七个独立的运动关节，可以在三维空间中执行更加复杂的运动。

七自由度机械臂的运动学逆解较为复杂，需要利用数学方法来求解。

三、机械臂的运动学建模机械臂的运动学建模是描述机械臂运动学性能的过程，它是机械臂控制的基础。

在进行运动学建模时，需要建立机械臂的坐标系，并推导出机械臂的正运动学方程。

对于七自由度机械臂来说，其正运动学方程通常可以表示为一个复杂的矩阵方程。

四、机械臂的运动学逆解求解方法机械臂的运动学逆解求解方法有多种，常用的方法包括解析法和数值法。

在解析法中，可以利用几何和代数方法进行分析，推导出七自由度机械臂的逆运动学方程。

而在数值法中，则可以借助数值计算软件如MATLAB来进行求解。

五、MATLAB求解七自由度机械臂的运动学逆解MATLAB是一款强大的科学计算软件，它具有丰富的数值计算函数和工具箱，可以方便地进行复杂的数值计算和仿真。

在求解七自由度机械臂的运动学逆解时，可以利用MATLAB的矩阵运算和符号计算功能，快速高效地求解出机械臂的关节角度。

六、七自由度机械臂运动学逆解的仿真利用MATLAB进行七自由度机械臂的运动学逆解仿真，可以直观地展示机械臂在给定位置下的关节角度和轨迹。

通过仿真可以验证逆解的准确性，同时可以对机械臂的运动学性能进行进一步分析和优化。

七、结论七自由度机械臂的运动学逆解是机械臂控制的关键问题，它直接影响着机械臂的运动精度和灵活性。

利用MATLAB进行运动学逆解的求解和仿真可以帮助工程师和研究人员更好地理解机械臂的运动学特性，为机械臂的控制和应用提供重要的参考和支持。

基于NX与Matlab/Simulink的协同仿真与应用1引言传统的机电产品设计中，机械结构设计和控制系统设计是各自独立的，分别采用功能不同的软件进行设计、调试和试验，最后通过物理样机，进行机械结构和控制系统的联合调试，如果发现问题，需要各自分别修改，然后再进行物理样机的制造和调试，这需要较长的开发周期[1]。

NX是当今世界最先进的CAD/CAM/CAE三维集成化软件之一，为用户提供了一整套集成的、全面的产品开发解决方案，用于产品设计、分析和制造，广泛应用于航空航天、汽车、通用机械和电子等工业领域。

Simulink是MA TLAB中的一种可视化仿真工具，它提供了一个动态系统建模、仿真和综合分析的集成环境，被广泛应用于控制理论和数字信号处理的复杂仿真和设计，是常用的控制系统设计软件之一。

利用NX与Simulink的协同仿真，可以将机械结构与控制系统设计仿真软件有机结合起来，然后对系统进行协同分析，直到获得满意的设计效果，这大大的提高了设计效率，缩短了开发周期，降低了开发产品的成本，获得了优化的系统整体性能。

本文介绍了NX8.0与Matlab/Simulink（2010A）协同仿真的方法，通过该方法，可充分发挥软件各自的特长，为复杂机电产品设计仿真提供一集成化平台。

2 NX与Simulink协同仿真流程NX与Matlab/Simulink实现协同仿真的流程如下：1）在NX中完成机械结构的设计。

2）在NX用户默认设置中指定可执行文件matlab.exe的位置（文件→用户默认设置→运动分析→分NX的运动仿真模块，指定动力学分析，高级解算方案选择协同仿真。

4）设置控制/动态解决方案。

解算方案类型选择常规驱动，分析类型选择控制/动力学。

5）根据具体情况创建运动副、连杆、标记点（Marker）、传感器等，传感器必须依靠标记点才能把信息通过工厂输出传递给控制系统。

6）创建工厂输入。

工厂输入是Simulink控制系统输出到NX机械机构信息的容器，Simulink中的控制系统把生成的输出信号保存在工厂输入中，工厂输入可以是力、扭矩等。

一、概述机械臂运动学逆解是指根据机械臂末端执行器的期望位置和姿态，计算机械臂各关节的角度。

这对于控制机械臂的运动非常重要，是实现机械臂精确定位和控制的基础。

在本文中，我们将使用Matlab编程实现机械臂运动学逆解，计算出机械臂的8个解。

二、机械臂运动学基础1. 机械臂基本结构和运动原理机械臂由多个关节信息组成，每个关节都可以实现转动。

通过控制各个关节的运动，可以实现机械臂的定位和控制。

2. 机械臂运动学正解和逆解机械臂的正解是指通过给定各个关节的角度，计算机械臂末端的位置和姿态。

而机械臂的逆解则是相反的过程，即根据末端位置和姿态，计算各个关节的角度。

三、Matlab编程实现机械臂逆解1. 设定机械臂末端位置和姿态我们需要给定机械臂末端的期望位置和姿态。

这通常通过末端执行器的笛卡尔坐标或欧拉角来描述。

2. 建立机械臂运动学模型接下来，我们需要建立机械臂的运动学模型。

这包括描述各个关节的运动规律，以及关节之间的几何关系。

3. 编写逆解算法根据机械臂的运动学模型，我们可以编写逆解算法。

这个算法可以根据末端位置和姿态，计算出机械臂的各个关节角度。

4. 考虑机械臂的特殊性在编写逆解算法时，需要考虑机械臂的特殊性，如关节限位、奇异点等问题。

确保逆解算法可以正确地处理这些情况。

四、计算机械臂的8个解在实际的计算中，机械臂的逆解通常具有多个解。

这是因为机械臂的自由度往往比末端的自由度要多，导致存在多个关节角度可以实现同一个末端位置和姿态。

在本文中，我们将使用Matlab编程计算机械臂的8个解。

五、总结通过Matlab编程实现机械臂运动学逆解，我们可以计算出机械臂的多个解。

这对于精确定位和控制机械臂运动非常重要，为机械臂的工程应用提供了有力支持。

六、参考文献以上是我根据您提供的主题和内容为您撰写的一篇文章，希望能对您有所帮助。

如需进一步了解或有其他需求，欢迎随时通联我。

为了更加深入地理解机械臂的运动学逆解和Matlab编程，我们将继续扩展本文的内容。

智能制造数码世界 P .287六轴机器人建模方法、正逆解、轨迹规划与实现张兴华 肖仕驰 广东白云学院摘要：本文用Matlab 实现六轴机器人的建模和实现轨迹规划。

讲解如何写正逆解以及轨迹插补的程序。

程序是基于Matlab2016a，工具箱版本为Robotic Toolbox 9.10。

关键词：六轴机器人 建模 Matlab1 D-H 建模三个两两相互垂直的XYZ 轴构成欧几里得空间，存在六个自由度：沿XYZ 平移的三个自由度，绕XYZ 旋转的三个自由度。

在欧几里得空间中任意线性变换都可以通过这六个自由度完成。

Denavit-Hartenberg 提出的D-H 参数模型能满足机器人学中的最小线性表示约定，用4个参数就能描述坐标变换：绕X 轴平移距离a；绕X 轴旋转角度alpha；绕Z 轴平移距离d；绕Z 轴旋转角度theta。

2 标准D-H 模型和改进D-H模型对比来看参数并没有改变，标准的 D-H 模型是将连杆的坐标系固定在该连杆的输出端（下一关节），也即坐标系i-1与关节i 对齐；改进的 D-H 模型 则是将坐标系固定在该连杆的输入端（上一关节），也即坐标系i-1与关节对齐i-1。

3 利用 Matlab Robotic Toolbox 建立机器人模型alpha:连杆扭角； a:连杆长度；theta:关节转角； d:关节距离； offset:偏移clear;clc;%建立机器人模型% theta d a alpha offsetL1=Link([0 0.4 0.025 pi/2 0 ]); %定义连杆的D-H 参数L2=Link([pi/2 0 0.56 0 0 ]);L3=Link([0 0 0.035 pi/2 0 ]);L4=Link([0 0.515 0 pi/2 0 ]);L5=Link([pi 0 0 pi/2 0 ]);L6=Link([0 0.08 0 0 0 ]);robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','manman'); %连接连杆，机器人取名manmanrobot.plot([0,pi/2,0,0,pi,0]);%输出机器人模型，后面的六个角为输出时的theta 姿态robot.display();其中表格为D-H 参数，grav 为重力加速度矢量，base 为基坐标系的齐次矩阵，tool 为工具坐标系和末端连杆的坐标系之间的变换矩阵。