多尺度几何分析概论

第22卷第7期计算机辅助设计与图形学学报V01．22 N o．7 2010年7月Journal of Co mp ut er—A id ed Desig n＆Co mp ut er Graphi cs July 2010几何曲面的双边滤波多尺度表示及几何细节增强肖春霞1’∞，冯光普¨，廖斌3’”(武汉大学计算机学院武汉430072)2’(武汉大学软件工程国家重点实验室武汉430072)3’(湖北大学数学与计算机科学学院武汉430062)(cx x i a o@w h u．e d u．o n)摘要：为了有效地对几何模型进行编辑建模及特征检测等处理，提出一种利用双边滤波对曲面进行多尺度表示及几何细节增强的算法．首先利用几何双边滤波对几何模型进行多尺度的分解，获取其多尺度的表示和多尺度的细节层；然后对不同尺度的几何细节进行自适应的增强，将这些增强的细节层与基曲面层进行重组，重建出一个几何细节增强的几何模型．利用几何模型的多尺度细节抽取，还提出一种几何细节迁移的算法，将抽取出的多尺度几何细节分解映射到其他几何模型的基曲面上，获取几何细节迁移的结果．文中算法实现简单、效率高，能有效地增强几何模型的几何细节，且整个几何模型不发生变形情况、保持几何特征．最后通过多个实例验证了该算法的有效性．关键词：双边滤波器；特征增强；多尺度曲面；几何细节迁移中图法分类号：TP391Multi。

scale Su r f a c e R e p r e s en t a t i o n a n d Detail Enhancement Bas ed on B il a te r al FilterXiao Chun xi91’∞，F eng Gu an gp u¨，an d L ia o Bin'3’"(S ch o ol of Comp u te r，Wu h an Unive rs it y。

第25卷第1期苏州市职业大学学报V ol.25，No.1 2014年3月Journal of Suzhou V ocational University Mar.，2014基于多尺度分析的图像去噪及特征提取算法研究戴桂平(苏州市职业大学 电子信息工程学院，江苏 苏州 215104)摘 要： 针对BEMD和非采样Contourlet变换2种典型的多尺度几何分析方法，研究并提出其在图像去噪及特征提取应用方面的4种算法模型，针对每种模型，分析了其算法原理及流程，并通过仿真实验验证了每种算法模型的有效性及优越性.关键词： 多尺度几何分析；二维经验模式分解；非采样Contourlet变换；独立成分分析中图分类号：TP391.41 文献标志码：A文章编号：1008-5475(2014)01-0017-05 Algorithms of Image De-noising and Feature ExtractionBased on Multi-scale AnalysisDAI Gui-ping(School of Electronic Information Engineering，Suzhou Vocational University，Suzhou 215104，China) Abstract：For two typical multi-scale geometric analysis methods：Bi-dimensional empirical modedecomposition and nonsubsampled contourlet transform，four algorithm models of image de-noising and featureextraction are proposed. For each model，the algorithm principles and processes are detailedly analyzed. Andthen through the simulation experiments，the effectiveness and superiority of each algorithm model are verified.Key words：multi-scale geometric analysis；bi-dimensional empirical mode decomposition；nonsubsampledcontourlet transform；independent component analysis在图像处理、模式识别与计算机视觉领域中，由于系统和环境等因素的影响，使得采集到的图像存在大量的噪声，视觉效果较差，直接影响了后续特征的提取，因而，图像去噪是图像处理的基础环节.此外，特征提取是模式识别的关键，全面、精确地提取特征是准确、快速分类的重要保证，因此图像去噪及特征提取成为一项十分重要的研究课题[1].近年来，随着对自然图像统计规律及人类视觉系统研究的深入，多尺度几何分析理论(multi-scale geometric analysis，MGA)逐渐成为计算机视觉领域的研究热点[2]. 所谓多尺度分析是指由粗到细或由细到粗地、在不同尺度(分辨率)上对图像进行分析，使其拥有方向性、多尺度、局部化、各向异性等优良特性，能够高效地捕捉自然图像的高维奇异性，其稀疏表达方式也更加符合人类视觉系统视皮层细胞感受野的处理机制.常用的图像MGA方法主要包括自适应和非自适应两类，自适应MGA方法是指图像变换的基函数随图像的具体内容而改变，包括Bandelet、Directionlet、Wedgelet以及EMD、BEMD等；而非自适应MGA方法是指基函数与具体的图像内容无关，包括Shearlet、Curvelet、Ridgelet、Contourlet以及非采样收稿日期：2013-11-21；修回日期：2013-12-22基金项目：国家自然科学基金资助项目(60970058)；江苏省自然科学基金资助项目(BK2009131)；苏州市职业大学青年基金资助项目(2013SZDQ02)作者简介：戴桂平(1982-)，女，江苏泰州人，讲师，硕士，主要从事模式识别与人工智能研究.第25卷 苏州市职业大学学报Contourlet 变换等[3]，其本质是通过对图像等高维数据内在的几何结构，如轮廓、边缘、纹理等进行高效地逼近和描述，从而克服了二维小波变换不能有效捕获信号高维奇异性的缺陷.其中，非采样Contourlet 变换除了继承多尺度几何分析的优良特性外，还具有多方向、各向异性、平移不变性以及基函数固定、结构更加稳定等性能，而二维经验模式分解(bi-dimensional empirical mode decomposition ，BEMD) 是一种具有自适应性的时频局部化多尺度分析方法，其分解不依赖于固定的基函数，因而能获得优良的图像处理性能.本文主要针对BEMD 以及非采样Contourlet(NSCT)变换这2种典型的多尺度几何分析方法，研究其在图像去噪、特征提取及模式识别中的应用.1 基于多尺度几何分析的图像去噪算法1.1 基于BEMD与双树复小波-局部Wiener滤波的图像去噪1) 基本原理.BEMD 是一种具有自适应性的时频局部化多尺度分析方法，与非自适应MGA 方法相比，此法能自适应地将图像和噪声逐级分解成若干个具有不同特征尺度的本征模函数(intrinsic mode function ，IMF)集，从而实现了图像与噪声的多尺度特征分离.与离散小波变换不同，双树复小波变换利用一对滤波器组同时产生两组小波分解，能够提供图像在6个高频方向的细节信息，因此具有平移不变性和良好的方向选择性、低冗余度以及完全重构特性等.而Wiener 滤波器是一种基于最小均方误差原则而得到的局部自适应线性滤波器，利用带有方向窗的局部Wiener 滤波可以对双树复小波分解得到的6个高频方向的细节信息进行去噪.2) 算法流程.结合BEMD 算法的自适应分解特性、双树复小波变换的平移不变性、多方向选择性以及Wiener 滤波优良的去噪性能，提出了一种基于BEMD 与双树复小波变换-局部Wiener 滤波相结合的图像去噪算法，具体见文献[4].该算法，首先，对含噪图像进行BEMD 分解得到不同特征尺度的IMF 子图像集；然后，利用双树复小波变换分别对中高频IMF 子图像进行多尺度、多方向分解，并结合带有椭圆方向窗的局部Wiener 滤波算法对各个高频方向子带进行去噪；最后，通过DTCWT 逆变换重构得到去噪后的IMF ，并与残差图像相加进行BEMD 重构，从而最终得到去噪后的图像.3) 仿真实验.为了验证去噪算法的有效性及优越性，文献[4]采用基于BEMD 与双树复小波-局部Wiener 滤波的图象去噪算法、BEMD 滤波、双树复小波-Wiener 滤波(2-DTCWT -Wiener)以及离散小波变换-Wiener 滤波(DWT -Wiener)分别对毫米波焦平面成像系统所形成的含有噪声的手枪图像进行去噪，结果如图1所示，实验结果表明，该融合算法去噪效果更明显，由于双树复小波变换可提供6个方向的高频细节信息且具备平移不变性，因而所提取的目标图像的边缘及细节特征更清晰，且不具有如图1(c)所示的Gibbs 现象的视觉失真.1.2 基于非下采样Contourlet变换(NSCT)域统计模型的自适应图像去噪1) 算法原理及流程.NSCT 是一种不进行下采样的Contourlet 变换，由非下采样金字塔(nonsub sampled pyramid ，NSP)和非下采样方向滤波器组(nonsub sampled directional filter banks ，NSDFB)构成，由于没有包含下采样环节，所以该变换具有平移不变性，此外还具有多方向性(任意方向)、各向异性等优良性能.基于NSCT 域统计模型的自适应图像去噪算法流程为：①NSCT 分解.对含噪图像进行3层(a) BEMD 滤波(b) 2-DTCWT -Wiener 滤波(c) DWT -Wiener 滤波(d) BEMD 与双树复小波-局部Wiener 滤波图1 各种算法去噪后的毫米波图像2014年第1期NSCT 分解，由粗到细尺度的方向数依次为4、8、16，得到低频及各尺度各方向的高频NSCT 系数.②基于各方向子带能量的改进BayesShrink 阈值估计.第i 尺度上噪声方差估计：利用蒙特卡罗鲁棒中值估计器来估计第i 尺度上所有方向子带系数的噪声方差σn2.i 尺度、j 方向子带贝叶斯阈值估计：利用最大似然估计法则估计i 尺度、j 方向上不含噪声的NSCT 系数方差，则贝叶斯阈值基于方向子带能量的改进BayesShrink 阈值估计为(1)式中：E j i 为第i 尺度、j 方向上的系数总能量；E i j j =∑1为第i 尺度上所有方向子带的系数总能量.由式(1)表明，方向子带能量越大，则细节信息越多，阈值越小；反之，方向子带能量越小，则含有的噪声越多，阈值则越大.③利用可调节的新阈值函数及改进的阈值对i 尺度、j 方向子带系数进行BayesShrink 收缩.具有可调节的新阈值函数为(2)式中：w i j k ,为第i 尺度、j BayesShrink 阈值. (3)④NSCT 重构.利用‘BayesShrink 改进算法去噪后的各个尺度的方向子带系数进行NSCT 重构，从而得到去噪后的图像.2) 仿真实验.为了验证基于NSCT 域统计模型的自适应图像去噪算法的优越性，将其与小波BayesShrink 去噪、Contourlet BayesShrink 去噪以及CT 改进BayesShrink 去噪相对比.其中，小波BayesShrink 去噪仿真中，利用bior4.4小波对含有噪声的仿真图像进行三层分解，利用未改进的BayesShrink 阈值对水平、垂直及对角高频系数分别进行收缩并重构；在Contourlet BayesShrink 去噪中，pfilt 和dfilt 滤波器分别采用‘9-7’及‘pkva ’系列，分解方向数矩阵nlevels 设定为[2，3，4]，即各4、8、16个高频方向；NSCT 改进BayesShrink 去噪中，pfilt 和dfilt 滤波器分别选择‘maxflat ’及‘dmaxflat7’系列，nlevels 仍设定为[2，3，4]，并采用峰值信噪比(PSNR)作为衡量去噪图像质量的指标.各种去噪算法PSNR值比较如图2所示，实验结果表明：NSCT 改进BayesShrink 去噪方法的去噪效果最好，PSNR 值最高为56.67 dB ；而Contourlet 变换由于不具备平移不变性，PSNR 值次之为47.08 dB ；CT BayesShrink 去噪中，由于其阈值及阈值函数不具备自适应性，PSNR 值只有31.90 dB ；在小波BayesShrink 去噪中，由于小波变换不具备多方向性及平移不变性，其去噪效果最差，PSNR 值仅为31.45 dB .2 基于多尺度几何分析的图像特征提取算法2.1 基于BEMD与ICAⅡ的图像特征提取1) 算法原理及流程.结合BEMD 算法的自适应时频局域化多尺度特性以及ICA Ⅱ表征数据的高阶图2 各种去噪算法PSNR值比较50100150200250501001502002505010015020025050100150200250(a) 小波BayesShrink 去噪(PSNR=31.45 dB)(b) CT BayesShrink 去噪(PSNR=31.90 dB)(c) CT 改进BayesShrink 去噪(PSNR=47.00 dB)(d) CT 改进BayesShrink 去噪(PSNR=56.67 dB)50100150200250501001502002505010015020025050100150200250 戴桂平：基于多尺度分析的图像去噪及特征提取算法研究第25卷 苏州市职业大学学报统计特性，提出一种基于BEMD 与ICA Ⅱ(独立成分分析，independent comment analysis)相结合的图像特征提取方法，具体见文献[5].该算法，首先，对预处理过的图像进行BEMD 分解，得到特征尺度从小到大(频率由大到小)的IMF 子图像集；然后，选取包含主要特征信息的若干IMF 子图像作为ICA Ⅱ的输入，为了减少计算量，采用PCA 算法去除子图像的二阶统计特征相关性进行降维；再次，利用FastICA Ⅱ算法提取IMF 子图像集的特征基向量；最后，利用提取的特征基向量进行图像的重构并通过分析重构信号的信噪比来验证(BEMD+ICA Ⅱ)图像特征提取算法的有效性与优越性.2) 仿真实验.为了验证(BEMD+ICA Ⅱ)图像特征提取算法的有效性及优越性，文献[5]将该算法成功地应用于掌纹识别领域.实验中BEMD 分解层数为5，并将分解后的5个IMF 子图像作为ICA Ⅱ的输入矩阵，采用随机采样大小为8×8像素的子图像块分别对每个IMF 抽取1 000次，从而构成大小为64×5 000的ICA Ⅱ输入矩阵，再利用基于PCA 降维处理的FastICA Ⅱ算法提取IMF 子图像集的掌纹特征基矩阵，其中PCA 主元个数取40，特征基矩阵维数为64×40，将其列向量转化成8×8的子图像块，从而构成图3(a)所示的40个特征基图像集，图3(b)为不经过BEMD 分解直接通过ICA Ⅱ提取出的特征基图像集，仿真结果表明，(BEMD+ICA Ⅱ)算法与单独的ICA Ⅱ相比，提取的特征基亮度变化更明显，具有更清晰的边缘，因而重构图像的信噪比更高，达到29.770 9，而后者仅为24.210 4.2.2 基于NSCT与改进脉冲耦合神经网络(M-PCNN)的图像特征提取1) 算法原理及流程.脉冲耦合神经网络(pulse coupled neural networks ，PCNN)是由Eckhorn 模拟猫的大脑视觉皮层中同步脉冲发放现象而建立的一个简化模型[6]，是由脉冲耦合神经元构成的二维单层、以迭代为主的自监督自学习网络，其中每个神经元与图像的每个像素相对应，其具有的连接域特性与动态阈值衰减特性能够使状态相似的神经元(像素)同步输出脉冲，从而能从复杂背景下提取出更多的图像细节信息.利用NSCT 分解的多尺度、多方向、各向异性、平移不变性以及M -PCNN 的全局耦合性和脉冲同步性，提出一种基于NSCT 和M -PCNN 的图像特征提取算法，流程为：①NSCT 分解.利用‘maxflat ’、‘dmaxflat7’型非下采样塔式及方向滤波器组对图像进行2层NSCT 分解，由粗到细尺度的方向数依次为2、4，得到低频子图及各尺度各方向上的高频子图集；②M -PCNN 二值图像信息熵特征矩阵提取.将低频子图及各尺度各方向的高频子图，分别输入简化后的M -PCNN 网络，模拟生物视觉的感知过程，通过迭代(设为20次)将每个子图分解成由若干(20个)二值图像组成的认知序列；利用信息熵公式计算每次迭代过程中输出二值图像Y ij (n )的信息熵，构成1×20维信息熵特征向量，并将低频及各方向高频子带提取的信息熵向量级联，构成整幅图像的信息熵特征向量，维数为1×(20×7)，20为每次迭代20次，7为子图总数(1个低频，6个方向高频子带).2) 仿真实验.为了验证(NSCT+M -PCNN)图像特征提取算法的有效性及优越性，采用ORL 人脸库进行实验，其中包括40人、每人10张人脸图像，前5张用于训练(200张)，后5张用于测试(200张)，利用NSCT+M -PCNN 算法分别提取训练集及测试集的二值图像信息熵特征矩阵(维数为140×200)，每一列对应一幅人脸图像的M -PCNN 信息熵特征向量，其中NSCT 参数设置见NST 分解，M -PCNN 采用简化的模型，具体参数设置为：连接强度系数β=0.4，耦合通道的固有电势V L =1，动态门限的固有电势V E =256，衰减时间常数αE =0.8，连接加权系数矩阵W =[0.5 1 0.5；1 0 1；0.5 1 0.5]，仿真结果如图4、图5所示，图4为NSCT 分解后的1个低频及6个高频方向子图，图5为coeffs{2}{1}高频子图(图4中第3个)输图3 (BEMD+ICAⅡ)与ICAⅡ提取的特征基图像及重构图像对比(a)基于BEMD 的ICA Ⅱ提取的特征基图像(b)基于ICA Ⅱ提取的特征基图像(c)( BEMD+ICA Ⅱ)重构掌纹图像(d) ICAⅡ重构掌纹图像2014年第1期出的12个M -PCNN 二值图像序列，程序中迭代次数为20次，应是20个二值图像，但其中8个二值图像信息熵为零或接近零，忽略不计，其对应的信息熵特征向量为H =[0.999 9，0，0，0.005 0，0.101 9，0.307 4，0.446 6， 0.535 3，0.460 2， 0.334 6，0.196 3，0.105 5，0.077 5，0.053 8，0.022 0，0.008 1，0.008 1，0.0027，0.002 7，0.001 4].由图4可知，人脸图像经过NSCT 多尺度、多方向稀疏分解后，得到1个低频子图和6个方向的高频子图，其中低频子图描述了人脸嘴、鼻、眼等方位信息；第1层的2个高频子图包含了大量用于识别的细节及边缘轮廓特征；而第2层的4个高频子图包含了更精细尺度的细节信息.将每个子图分别输入到M -PCNN 网络，得到一系列二值图像的信息熵特征向量，由于不同人脸图像像素分布的差异性，其生成的二值认知序列也具备明显差异，且信息熵特征具有旋转、平移、缩放及局部变形不变性，因而此算法提取的图像特征具备对图像尺度、旋转、变形和光照强度不变的优良特性.3 结论本文主要针对2种典型的多尺度几何分析方法：BEMD 以及非采样Contourlet 变换(NSCT)，研究其在图像去噪及特征提取中的应用，阐述并提出了4种算法模型，即基于BEMD 与双树复小波-局部Wiener 滤波的图像去噪算法、基于非下采样Contourlet 变换(NSCT)域统计模型的自适应图像去噪算法、基于BEMD 与ICA Ⅱ的图像特征提取算法以及基于NSCT 与改进脉冲耦合神经网络(M -PCNN)的图像特征提取算法，针对每种模型，分析了其算法原理及流程，并通过仿真实验验证了每种算法模型的有效性及优越性，从而为图像处理、人体生物特征识别技术提供一种更为有效的方法及新思路.参考文献：[1] 刘丽，匡纲要. 图像纹理特征提取方法综述[J]. 中国图象图形学报，2009，14(4)：621-632.[2] 李财莲，孙即祥，康耀红. 图像多尺度几何分析综述[J]. 海南大学学报：自然科学版，2011，29(3)：275-281.[3] 李彦，汪胜前，邓承志. 多尺度几何分析的图像去噪方法综述[J]. 计算机工程与应用，2011，47(34)：168-173.[4] 戴桂平，林洪彬. 基于BEMD 与双树复小波-局部Wiener 滤波的毫米波图像去噪[J]. 机械设计，2011，28(9)：12-16.[5] 戴桂平，尚丽. 应用二维EMD 和独立成分分析的掌纹识别[J]. 计算机工程与应用，2011，47(19)：182-185.[6] 王朝晖，王佳琪，赵德功，等. 基于Shearlet 与改进PCNN 的图像融合[J]. 激光与红外，2012，42(2)：213-215.(责任编辑：沈凤英)图4 人脸图像NSCT两层分解(1个低频，6个高频)图5 coeffs{2}{1}高频子图输出的M-PCNN二值图像序列戴桂平：基于多尺度分析的图像去噪及特征提取算法研究。

文章来源：安世亚太官方订阅号（搜索：peraglobal）随着增材制造领域中3D打印技术的快速发展，增材点阵结构在航天航空、船舶、汽车、体育和医疗等行业得到了广泛应用，如图1所示。

点阵结构作为一种新型的结构设计，除轻量化特点外，同时还具有优良的比刚度/强度、阻尼减震、缓冲吸能、吸声降噪以及隔热隔磁等功能性特点。

由于其含有大量复杂的微观结构，包括胞元类型和几何尺寸等参数，导致建模和仿真计算工作量巨大，传统有限元分析已经无法适用。

因此，经过多年的仿真计算积累和努力探索，我们团队开发出了一款专业用于增材点阵结构仿真分析的软件，即Lattice Simulation。

本文分为上、下两篇，上篇结合应用案例，浅谈基于多尺度算法开发出的这款点阵结构分析工具，是如何高效、快速地帮助用户解决增材点阵结构设计中遇到的CAE分析问题的。

下篇将对Lattice Simulation和ANSYS Discovery进行分析对比，以说明多尺度算法在点阵结构分析中的准确性。

图1 点阵结构1、概述Lattice Simulation是一款用于增材点阵结构分析的工具，具有用户自定义和内置点阵结构设计两种方式，已集成在ANSYS add-in扩展工具中。

基于多尺度算法，用户可以采用等效均质化技术对点阵结构进行有限元分析。

并且提取非均质化点阵结构的等效材料参数，在均质化等效实体模型宏观力学分析后，可以通过局部分析对胞元结构进行详细的应力校核。

图2 点阵结构分析工具功能图3 Workbench点阵结构模块分析流程2、Lattice Simulation功能与优势Lattice Simulation提供增材点阵结构在有限元仿真中涉及的相关分析功能（1）均质化分析基于胞元结构类型及在空间上的周期排列特性，进行均质化计算，提取等效实体的材料力学特性。

（2）宏观分析采用均质化分析得到的等效材料数据，并对等效实体点阵结构进行力学分析，校核点阵结构刚度性能。

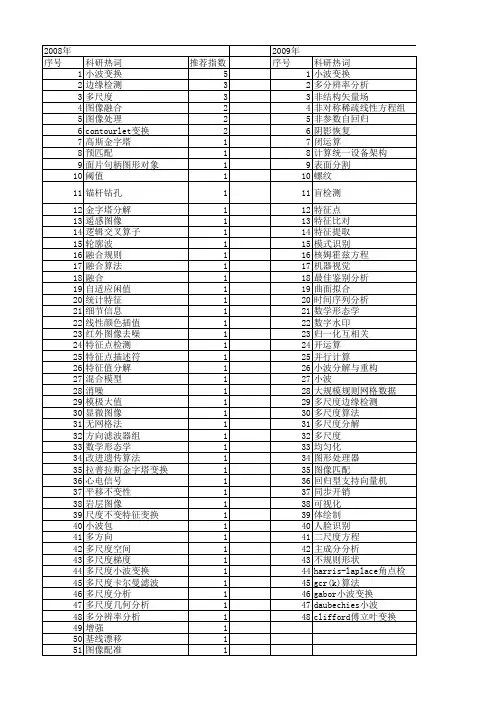
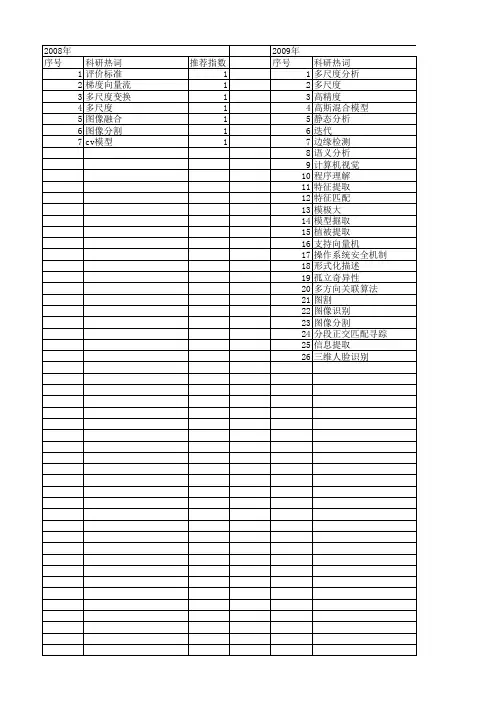
Bandelet变换原理及应用研究杨思燕【摘要】In recent years,multi-scale geometric analysis (MGA) has been widely used for research and applications in statistical analysis,pattern recognition,signal processing and digital image processing,etc.As an adaptive MGA method,Bandelet transform can track geometrical regularity of image structure adaptively and represent sharp image transition.Being able to provide the sparsest representation,Bandelet could use less nonzero coefficients to reach the same identification effect as other basic functions,especially more superior in image with significant geometric features.Introduced the development and principles of Bandelet transform in detail,and further researched the application in imagesmoothing,compression,segmentation and fusion.Finally trend in development were also pointed out.%近年来,多尺度几何分析在统计分析、模式识别、信号处理、数字图像处理等领域中应用广泛.作为自适应多尺度几何分析的一种新方法,Bandelet变换侧重于图像边缘的表示和处理,对于图像中的几何正则方向具有较强的自适应跟踪能力,由于Bandelet变换能提供对图像的最稀疏表示,能够用比别的基函数更少的非零系数来达到同样的逼近效果,特别是对几何特征明显的图像更具优势.文中详细介绍了Bandelet变换的提出、基本原理和方法等技术实现细节,探讨和和分析了Bandelet变换在数字图像的压缩、融合、去噪和分割等诸多方面的应用,并探讨了Bandelet变换技术的应用发展趋势.【期刊名称】《计算机技术与发展》【年(卷),期】2013(023)007【总页数】6页(P233-237,241)【关键词】多尺度几何分析;小波变换;Bandelet变换;去噪;压缩【作者】杨思燕【作者单位】陕西广播电视大学计算机与信息管理系,陕西西安710119【正文语种】中文【中图分类】TP390 引言多尺度集合分析(Multiscale Geometric Analysis，MGA)近年来在信号处理、数学分析、计算机视觉和模式识别等学科和领域应用广泛，发展迅速。

多尺度检测（特征⾦字塔）（空间⾦字塔池化）（融合多层信息）的好处多尺度检测（不同的idea）（特征⾦字塔）（空间⾦字塔池化）（带洞空间⾦字塔池化）（融合深浅层特征）检测和分割中的例⼦分割： sppnet中的spp空间⾦字塔池化结构；(spatial pyramid pooling) pspnet中的pyramid pooling moudle结构，综合讲是⾦字塔场景解析结构； deeplabv3+中的aspp结构，以及解码过程中联合编码部分信息的构造；(atrous spatial pyramid pooling)检测： ssd中的使⽤多尺度的特征图投向最后的检测器； yolov3中使⽤的三个不同尺度，⼩尺度上采样融合前⾯特征变成⼤尺度； FPN中的top-down结构，各种改造的特征⾦字塔（NAS-FPN、panet、Bifpn）； trident net中的三叉戟结构，类似aspp结构；　根据不同的任务，下⾯的理由适合解释多尺度的好处。

深层浅层map信息特征深层⽹络的感受野⽐较⼤，语义信息表征能⼒强，但是特征图的分辨率低，⼏何信息的表征能⼒弱（空间⼏何特征细节缺乏）；低层⽹络的感受野⽐较⼩，⼏何细节信息表征能⼒强，虽然分辨率⾼，但是语义信息表征能⼒弱。

⾼层的语义信息能够帮助我们准确的检测或分割出⽬标。

深浅层对应适合的⽬标⼤⼩下采样倍数⼩（⼀般是浅层）的特征感受野⼩，适合处理⼩⽬标，⼩尺度map（深层）分辨率信息不⾜不适合⼩⽬标在yolov3中对多尺度检测的理解是，1/32⼤⼩的特征图（深层）下采样倍数⾼，所以具有⼤的感受野，适合检测⼤⽬标的物体，1/8的特征图（较浅层）具有较⼩的感受野，所以适合检测⼩⽬标。

FPN中的处理在下⾯。

对于⼩⽬标，⼩尺度feature map⽆法提供必要的分辨率信息，所以还需结合⼤尺度的feature map还有个原因是在深层图做downsample损失过多信息，⼩⽬标信息或许已经被忽略。