基于灵敏度分析的有限元模型修正

基于Kriging模型的有限元模型修正方法研究基于Kriging模型的有限元模型修正方法研究摘要：有限元模型是一种常用的结构分析方法，然而，由于模型假设和离散化误差等因素，其结果可能存在一定误差。

本文提出了基于Kriging模型的有限元模型修正方法，通过对已有有限元模型数据进行拟合，进而修正模型中的误差，并对修正效果进行验证。

实验结果表明，基于Kriging模型的有限元模型修正方法能够显著提高有限元模型的精度和稳定性。

关键词：有限元模型；Kriging模型；模型修正；精度；稳定性1. 引言有限元模型是一种常用的结构分析方法，广泛应用于工程领域。

然而，在实际应用过程中，由于对结构复杂性的简化、参数估计误差以及离散化误差等因素的影响，有限元模型的分析结果可能存在一定误差，从而影响工程设计的准确性。

因此，如何对有限元模型进行修正并提高其精度和稳定性成为了一个重要的研究方向。

2. Kriging模型的基本原理Kriging模型是一种基于统计学的插值方法，通过对已有样本数据的拟合，预测未知位置上的数值。

其基本思想是通过已知样本点之间的空间相关性，在未知位置上进行插值，从而得到预测结果。

Kriging模型通过建立样本点之间的半变异函数，从而描述其空间相关性，并通过最小化预测误差来确定未知位置上的数值。

3. 基于Kriging模型的有限元模型修正方法基于Kriging模型的有限元模型修正方法主要包括以下几个步骤：（1）数据采集：首先，需要采集与有限元模型相关的数据，包括原始模型的力学性能、结构几何参数、材料参数等。

（2）数据预处理：对采集到的数据进行预处理，包括数据的筛选、去噪和归一化处理等，以减小数据误差对模型修正的影响。

（3）Kriging模型构建：根据预处理后的数据，构建Kriging模型，包括选择合适的半变异函数、估计其参数，并进行模型的验证。

（4）有限元模型的修正：利用步骤（3）中构建的Kriging模型，对已有的有限元模型进行修正，得到修正后的模型。

O29，O177.922007020132一类两相同部件并联可修系统的稳定性/王定江(浙江工业大学理学院)//浙江工业大学学报.―2006，34（2）.―228～229，236.可修系统是可靠性理论研究的主要内容，可修系统包含串联和并联系统，并联系统是指系统中的多个部件有一个完好系统就能正常工作的一类系统。

该文讨论一类两相同部件并联可修系统的数学模型，应用强连续算子半群证明了系统的非负解的存在唯一性，讨论了系统的稳定性。

图0表0参9O29，O352007020133具有超薄厚度的多孔介质中St okes流的均匀化/赵红星，姚正安(中山大学数学与计算科学学院)//中山大学学报（自然科学版）.―2006，45（3）.―5～8.主要研究了在三维的多孔介质中具有超薄厚度的区域上Stokes流的均匀化。

经过细致地分析，文章最后论证了当流体区域的厚度充分小时，流体的运动状态满足平面流中的“达西定律”。

图0表0参10TB1142007020134小子样条件下基于N or m al-Poi s s on过程的性能可靠性评定/张永强，刘琦，周经伦(国防科技大学信息系统与管理学院)//国防科技大学学报.―2006，28（3）.―128～132.对于高可靠、长寿命产品，基于性能退化数据分析可靠性是一种行之有效的技术途径。

结合航空航天产品性能退化的机理与现场试验小子样的特点，建立了基于Normal-Pois son过程的性能退化模型。

论文在对产品性能退化建模的基础上，结合Bayes方法给出了退化模型参数的估计算法和可靠性推断的公式，最后结合实例说明了方法的有效性。

图0表2参13TB114.32007020135基于G A的可靠性寿命分布参数的极大似然优化估计/方华元，胡昌华，樊红东，丁力(西安第二炮兵工程学院)//上海航天.―2006，23（2）.―50～53.基于极大似然估计法的基本原理和优化理论，建立了可靠性寿命分布参数的极大似然优化估计模型，并采用遗传算法（GA）进行求解。

基于Tikhonov正则化迭代求解的结构损伤识别方法夏志鹏; 王树青; 徐明强; 王皓宇【期刊名称】《《振动与冲击》》【年(卷),期】2019(038)017【总页数】9页(P251-259)【关键词】海洋平台; 损伤检测; 交叉模态应变能; Tikhonov正则化; 噪声鲁棒性【作者】夏志鹏; 王树青; 徐明强; 王皓宇【作者单位】中国海洋大学海洋工程系山东青岛266100【正文语种】中文【中图分类】TU317海洋平台结构长期服役在恶劣的海洋环境中，容易产生各种形式的损伤，使结构的承载能力下降，甚至导致平台失效，造成巨大经济损失及人员伤亡[1]。

因此，针对海洋平台结构的健康监测与损伤识别非常重要。

目前结构损伤检测的方法众多[2-3]，基于振动测试的结构健康监测技术相对较为简单且成本较低，是非常具有发展前景的损伤识别技术[4]。

其中，基于模态参数的损伤检测是近年来新兴且有效的检测手段。

在某些情况下，基于模态参数的结构损伤识别过程可以简化为线性方程组Cα=b 的求解问题。

当不考虑测量噪声或噪声干扰较小时，该系统的求解往往可以得到满意的结果；而当结构测量模态信息受噪声影响较为严重时，系统的求解结果往往会振荡发散，导致检测方法失效。

因此，噪声鲁棒性是此类损伤识别技术在发展过程中必须考虑的问题。

从数学的角度看，利用结构的振动测试数据识别其损伤是求解反问题的过程，其不适定性体现在所构建系统的病态上，即微小的测量误差都可能导致解的振荡发散。

为解决这一问题，学者们做了大量研究[5-11]。

其中，基于Tikhonov正则化[12]的方法应用较为广泛，其基本思想是：用一族与原问题相“邻近”的适定问题的解去逼近原问题的真实解。

王艺霖等将Tikhonov 正则化方法用于结构的损伤识别，一定程度上改善了系统的不适定性，提高了损伤识别精度，并指出正则化方法的作用可通过刚度矩阵条件数的减小来明确衡量。

Hua等将Tikhonov正则化与基于灵敏度分析的有限元模型修正方法相结合，进行了简单框架结构的损伤识别，该方法体现出较好的抗噪性。

基于kriging模型的有限元模型修正方法研
究
有限元模型是机械设计中不可或缺的工具，然而模型的精度往往
受限于建模时的假设和误差。

本文介绍了一种基于克里格模型的有限
元模型修正方法，旨在提高有限元模型的精度和可靠性。

克里格模型是一种基于统计学原理的插值模型，可以根据已知的
数据点生成预测值。

在有限元模型修正中，克里格模型经常用于解决
数据不充分的问题。

当有限元模型的误差与某些参数相关联时，克里
格模型可以对这些参数进行建模，并在未知点处生成较为准确的预测值。

具体地说，有限元模型的修正过程如下：首先获取一组真实的数
据点和与之相对应的有限元模型的预测值，并建立一组参数模型。

然后，使用克里格模型根据已知数据点生成修正值，并将其添加到原模
型预测值中。

最后，重新运行有限元模型，比较修正后的结果与真实
数据的误差，如果误差得到了显著改善，那么该方法就被认为是有效的。

修正过程可能涉及的参数包括材料属性、几何结构、边界条件等，而确定这些参数的方法可以是试验测试、数值模拟或者响应面分析。

当然，参数模型的建立也需要充分的数据支持，否则容易产生过拟合
或欠拟合的问题，导致修正后的模型并无任何实际意义。

总的来说，基于克里格模型的有限元模型修正方法是一种直观、可靠且易于实现的方法，可以为机械设计师提供更加精确和可信赖的有限元模型。

然而，该方法仍然存在一定的局限性，特别是在数据不足和参数之间高度耦合的情况下。

因此，在实际应用时需要综合考虑各种因素，做出最优化的决策。

第２１卷第９期２０２３年９月动力学与控制学报J O U R N A L O FD Y N AM I C SA N DC O N T R O LV o l ．２１N o ．９S e p．２０２３文章编号:１６７２Ｇ６５５３Ｇ２０２３Ｇ２１(９)Ｇ０２３Ｇ０１０D O I :１０．６０５２/１６７２Ｇ６５５３Ｇ２０２２Ｇ０４１㊀２０２２Ｇ０８Ｇ１７收到第１稿,２０２２Ｇ０９Ｇ１３收到修改稿．∗国家自然科学基金(１２０７２１８１,１１７０２１７０)和机械系统与振动国家重点实验室课题资助项目(M S V ２０２１０５),N a t i o n a lN a t u r a l S c i e n c eF o u n Ｇd a t i o no fC h i n a (１２０７２１８１,１１７０２１７０)a n d t h eS t a t eK e y L a b o r a t o r y o fM e c h a n i c a l S y s t e m s a n dV i b r a t i o n (M S V ２０２１０５)．†通信作者E Ｇm a i l :w e i s h a １２１９＠１２６．c o m基于K r i g i n g 模型的航空发动机管道系统有限元模型修正∗陈奕丰１㊀范鑫２㊀魏莎１,３†㊀郑冰月１㊀丁虎１,３㊀陈立群１,３(１．上海大学力学与工程科学学院,上海㊀２００４４４)(２．中国科学技术大学工程科学学院,合肥㊀２３００２６)(３．上海市应用数学和力学研究所,上海㊀２０００７２)摘要㊀为获得精确可靠的航空发动机外部管道结构动力学模型,采用将K r i g i n g 模型与多目标遗传算法(MO G A )相结合的模型修正方法进行有限元模型修正．首先进行管道模型的模态试验和有限元建模,分别获得模态参数的试验值和有限元分析值;然后在合理的参数选取和试验设计(D O E )的基础上,拟合得到K r i g i n g 模型;最后基于K r i g i n g 模型采用多目标遗传算法进行有限元模型修正,并对比了不同修正方法的精度和修正效果．结果表明:采用K r i g i n g 模型进行有限元模型修正可以有效提升修正效果,获得更为准确的有限元模型;对于航空发动机管道系统,基于K r i g i n g 模型的模型修正方法相较于基于灵敏度分析的模型修正方法具有更高的修正效率和修正精度．关键词㊀管道,㊀有限元模型修正,㊀模态分析,㊀K r i g i n g 模型,㊀灵敏度分析中图分类号:V ２３３;T H １１３．１文献标志码:AF i n i t eE l e m e n tM o d e lU p d a t i n g o f a nA e r o e n g i n eP i pe S y s t e mB a s e do nK r i g i n g Mo d e l ∗C h e nY i f e n g １㊀F a nX i n ２㊀W e i S h a １,３†㊀Z h e n g B i n g y u e １㊀D i n g H u １,３㊀C h e nL i qu n １,３(１．S c h o o l o fM e c h a n i c s a n dE n g i n e e r i n g S c i e n c e ,S h a n g h a iU n i v e r s i t y ,S h a n gh a i ㊀２００４４４,C h i n a )(２．S c h o o l o fE n g i n e e r i n g S c i e n c e ,U n i v e r s i t y o f S c i e n c e a n dT e c h n o l o g y ofC h i n a ,H e f e i ㊀２３００２６,C h i n a )(３．S h a n g h a i I n s t i t u t e o fA p p l i e d M a t h e m a t i c s a n d M e c h a n i c s ,S h a n gh a i ㊀２０００７２,C h i n a )A b s t r a c t ㊀I no r d e r t oo b t a i na na c c u r a t ea n dr e l i a b l ed y n a m i cm o d e l o f a e r o e n g i n ee x t e r n a l p i p es t r u c Ｇt u r e s ,t h e f i n i t e e l e m e n tm o d e l (F E M )i s u p d a t e db y c o m b i n i n g t h eK r i g i n g m o d e l w i t h t h em u l t i Ｇo b j e c Ｇt i v e g e n e t i c a l g o r i t h m (MO G A )．F i r s t l y ,b o t h t h em o d a l t e s t a n d t h e f i n i t e Ｇe l e m e n t a n a l ys i s a r e c o n d u c Ｇt e d t o i d e n t i f y t h e d y n a m i c c h a r a c t e r i s t i c s o f t h e p i p e l i n em o d e l ．T h e n ,b a s e d o n t h e s e l e c t e d p a r a m e t e r s a n dD e s i g no f E x p e r i m e n t (D O E ),t h eK r i g i n g s u r r o g a t em o d e l s o f t h e F E Mo f p i p e a r e s e t u p b y me a n s of f i t t i ng ．F i n a l l y ,b a s e do nK r i g i n g s u r r o g a t em o d e l s ,th eF E Mi s u p d a t e db y MO G A ;t h e c o m pa r i s o n i s c o n d u c t e do n t h e a c c u r a c y a n du p d a t i n g e f f e c t o f d i f f e r e n tm o d e l u p d a t i n g me t h o d s ．T h e r e s u l t s s h o w t h a t t h eK r i g i n g s u r r o g a t em o d e l c a nb e a p p l i e d t ou p d a t e t h eF E M ,w h i c hw i l l g r e a t l y i m p r o v e t h e ef f i Ｇc i e n c y a n d a c c u r a c y i n c a l c u l a t i o n ．T h eK r ig i n g m o d e lm e th o d h a s o b vi o u s a d v a n t a g e s o v e r t h e s e n s i t i v i t y a n a l y s i sm e t h o d f o r a e r o e n g i n e p i pe s t r u c t u r e ．K e y wo r d s ㊀p i p e ,㊀f i n i t e e l e m e n tm o d e l u p d a t i n g ,㊀m o d a l a n a l y s i s ,㊀K r i g i n g m o d e l ,㊀s e n s i t i v i t y a n a l Ｇys i s动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２３年第２１卷引言航空发动机外部管路是航空发动机的重要组成部分,如同血管一般为航空发动机输送燃料㊁液压油等工作介质．由于航空发动机外部管路具有结构的复杂性㊁激励的多源性以及耦合的关联性,在其工作过程中极易发生管路系统共振,从而降低整个系统的安全可靠性[１,２]．目前航空发动机管路的振动特性分析多聚焦于流固耦合方面,缺少对管道模型结构本身的研究．为此,针对航空发动机外部基本管道建立精确的有限元模型是十分必要的．在工程设计阶段,基于已有参数建立的有限元模型由于受到局部网格划分㊁材料参数不确定以及模型固有的阶次误差㊁离散误差等因素的影响[３],有限元模型预测结果与实验结果之间会存在一定误差,从而使得初始模型很难反映实际几何结构．为保证模型的状态预测㊁分析与评估具有实际意义,需要基于模态试验数据对初始有限元模型加以修正．有限元模型修正的本质在于通过修正有限元模型中的相关参数,缩小有限元模拟结果与试验实测结果之间的误差,从而建立出更高精度的有限元模型,以替代实际结构进行分析与监测．传统的模型修正方法主要分为矩阵法和参数法[４]．参数法通过调整设计参数以实现修正目标,同矩阵法相比更容易在工程中实现应用．代理模型方法是参数法中应用十分广泛的一种．所谓代理模型,通常是指在分析和优化设计过程中可替代那些比较复杂和费时的数值分析的近似数学模型,也称为响应面模型㊁近似模型或元模型[５,６]．使用代理模型方法可以极大地提高计算效率,还能同其他优化算法相结合．常用的代理模型有多项式响应面模型[７,８]㊁径向基函数模型[９,１０]和K r i g i n g模型[１１,１２]等．K r i g i n g模型是一种基于随机过程的代理模型,被称为样本点的无偏线性估计函数[１３]．K r i g i n g模型在结构优化与可靠性分析领域中应用广泛,其优势在于针对非线性结构进行模型修正具有较强的适用性,在较少样本点的情况下依然能保障较高的修正精度．该模型不仅在地质㊁水文㊁气象㊁环境科学等自然科学领域得到应用,也在航空航天㊁汽车等工程科学领域得到研究㊁发展和应用[１４]．例如,王文竹等[１５]引入K r i g i n g模型,对鼓式制动器稳定性进行了优化设计,抑制了制动噪声;张文鑫等[１６]使用自适应K r i g i n g结合M o n t eC a r l o模拟以及所提停止准则计算了涡轮盘盘心低周疲劳寿命可靠性,验证了该方法的可靠性;C u i等[１７]将K r i g i n g模型引入空间仪器的热模型修正中,使模型区域的温度值与热平衡实验结果相接近;Y i n等[１８]构建了K r i g i n g模型㊁二次多项式模型和径向基函数模型三种代理模型,针对平面桁架有限元模型进行了有限元模型修正,并对比了三种方法的异同．本文以航空发动机管道模型为研究对象,通过模态试验和有限元建模得出管道模态试验值和有限元分析值,然后选取合适的待修正参数和试验设计(D e s i g n o fE x p e r i m e n t,D O E)方法,构建出K r i g i n g代理模型．利用构建好的代理模型代替有限元模型,基于多目标遗传算法(m u l t io b j e c t i v e g e n e t i c a l g o r i t h m,MO G A)实现对管道模型的有限元模型修正．通过将采用K r i g i n g模型的修正结果与灵敏度分析方法的修正结果进行对比,验证了所用模型修正方法的可行性．１㊀管道模态试验１．１㊀模态试验方案选取某航空发动机管道模型作为研究对象．管道部件由导管㊁堵头㊁锁紧螺母㊁支座㊁垫圈㊁直通管接头㊁扩口式平管嘴和外套螺母构成,管道模型结构如图１所示．图１㊀管道模型结构示意图F i g．１㊀S c h e m a t i c d i a g r a mo f t h e p i p em o d e l s t r u c t u r e４２第９期陈奕丰等:基于K r i g i n g 模型的航空发动机管道系统有限元模型修正模型中导管为两端带扩口的直径６mm ,壁厚０．６m m 的５００m m 不锈钢直管,密度为７９３０k g/m ３,弹性模量为１９４G P a ,泊松比为０．３．导管与支座之间采用螺栓连接方式,外套螺母和管嘴起到导管与直通管接头之间的密封连接作用．整体模型通过沉头螺栓紧固安装在铸铁试验台上,最大程度上降低了环境的影响．由于本文主要分析管道系统中硬管干模态下的振动特性,故忽略模型两端软管及其连接件,模型各组件材料参数如表１所示．表１㊀管道模型各组件材料参数T a b l e １㊀M a t e r i a l p a r a m e t e r s f o r e a c hc o m po n e n t o f t h e p i pem o d e l A s s e m b l yu n i t D e n s i t y (g c m －３)M o d u l u s o fe l a s t i c i t y/G P a P o i s s o nr a t i o P i pe l i n e ７．９３０１９４０．３P l u g g i n g h e a d ７．８５０２１００．３１L o c kn u t ７．８５０２１００．３１W a s h e r１１．３４４１７０．４２P i p e jo i n t ７．８５０２１００．３１S l e e v e n u t４．５１０１１００．３４F l a r e dn o z z l e ７．９３０１９４０．３S u p po r t ２．８１０７１０．３３为分析系统模态特性,选用L M S 数据采集仪㊁P C B 冲击锤和P C B 单轴加速度传感器对管道模型进行模态试验,试验模态测试系统如图２所示．图２㊀试验模态测试系统示意图F i g ．２㊀S c h e m a t i c d i a g r a mo fm o d e t e s t s ys t e m 在试验模态测试过程中,利用冲击力锤施加脉冲激励,采用单点激励多点响应的形式[１９],将力传感器信号和拾振点处单轴加速度传感器信号反馈给数据采集系统,采集输入输出信号,基于多参考点最小二乘复频域方法(P o l yr e f e r e n c el e a s t Ｇs q u a r e s c o m p l e x f r e q u e n c y Ｇd o m a i nm e t h o d ,P o l y ＧMA X )[２０]对输入输出信号进行分析处理,进而获得系统模态参数．在导管表面从端部起每隔５０mm 布置一个测点,共布置１１个测点,如图３所示．为确保试验结果真实有效,每次敲击均由同一名试验人员依次对测点进行横向激励并进行５次有效平均．图３㊀测点布置示意图F i g ．３㊀S c h e m a t i c d i a gr a mo fm e a s u r e m e n t p o i n t s １．２㊀试验结果分析基于上述试验测试方案,得出管道模型前５阶模态频率为１２８．７６H z ㊁２１８．６２H z ㊁４０９．３７H z㊁６５１．５６H z ㊁１０４９．７６２H z ．试验模型的前５阶模态振型如图４所示．图４㊀模型前５阶模态振型示意图F i g ．４㊀S c h e m a t i c d i a g r a mo f t h e f i r s t f i v em o d a l s h a p e s o f t h e s ys t e m 管道模型整体在－z 方向力锤激励下发生横向振动,随着模态阶次的增加,振型中波数和节点数随之增加．由第二阶振型㊁第四阶振型和第五阶振型可以明显看出,管道端部存在较大的位移．因此,建模时不能仅将导管端部视为固定端约束,需要考虑到管道端部连接结构对试验模型整体模态的影响．５２动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２３年第２１卷２㊀管道有限元建模及分析针对直管管道试验模型,采用S O L I DWO R K S三维建模软件和A N S Y S 有限元软件进行了有限元建模㊁网格划分和动力学特性分析．在A N S Y S中建立的有限元模型如图５所示．导管部分采用六面体单元(H E X A )划分网格,两端连接组件及支座部分采用四边形单元(Q U A D ４)划分网格,共２５３０９个单元．根据接触设置分析算例[２１]并结合工程实际,将与直通管接头外圆柱面接触的外套螺母㊁锁紧螺母㊁堵头等组件与直通管接头之间的接触方式设置为绑定接触,其余接触均设置为粗糙接触,支座底面设置为固定端约束面．使用A N S Y S 对有限元模型进行模态分析,提取前５阶模态参数结果,模态频率的对比结果如表２所示．有限元分析结果与实测模态结果中,模态频率误差在２０％以内,各阶振型无较大差异,具有一定的相关性．同时,实测模态频率与有限元分析结果相比最大误差达到８．６０％,各阶误差均超过５％,超出工程实际中可接受的范围,有必要进行有限元模型修正．为探究支座及管接头组件对有限元模型的影响,建立了去除全部管接头组件的有限元模型A 和仅去除支座的有限元模型B 并分别进行模态分析,模态频率结果如表２所示．模型A 的最大误差达到７６．５８％,模型B 的最大误差达到９３．７５％,误差远超过工程实际中可接受的范围．模型A 和模型B 与实际结构之间存在振型不匹配现象．相比于模型A 和模型B ,完整模型的模态参数更加接近于实测模态参数．可见支座和管接头连接组件对试验模型整体模态参数具有较大影响,建模时应予以保留．表２㊀计算模态频率与实测模态频率的对比T a b l e ２㊀C o m p a r i s o no f c a l c u l a t e dm o d a l f r e q u e n c i e s a n dm e a s u r e dm o d a l f r e qu e n c i e s M o d e M e a s u r e dv a l u e /H z C o m pl e t em o d e l C a l c u l a t e dv a l u e /H z E r r o r/％M o d e lAC a l c u l a t e dv a l u e /H z E r r o r /％M o d e l BC a l c u l a t e dv a l u e /H z E r r o r /％１１２８．７６１３６．４３５．９６１２９．９３０．９１１４３．７１１１．６１２２１８．６２２３１．０３５．６８３５７．３７６３．４７３９４．３４８０．３８３４０９．３７４３４．４４６．１２６９８．５４７０．６４７６８．７９８７．８０４６５１．５６６９６．６４６．９２１１５０．５０７６．５８１２６２．４０９３．７５５１０４９．７６１１４０．００８．６１７１１．２０６３．０１１８７０．７０７８．２０图５㊀系统有限元模型F i g ．５㊀F i n i t e e l e m e n tm o d e l o f t h e s ys t e m ３㊀管道有限元模型修正基于K r i g i n g 模型的有限元模型修正流程如图６所示．可大致概括为３个主要流程:①将模态试验实测数据与有限元模型模拟结果进行自由度匹配与相关性分析,确保有限元模型与实际结构具有一定的相关性．其中,若有限元分析频率与实测模态频率的误差在２０％以内且有限元分析振型与实测模态振型之间无较大差异,则视为满足相关性条件．②K r i g i n g 模型的生成．首先选取合适的待修正参数并进行试验设计,使得在一定的样本空间内图６㊀基于K r i g i n g 模型的有限元模型修正流程图F i g ．６㊀F l o wd i a g r a mo f f i n i t e e l e m e n tm o d e l u p d a t i n gb a s e do n t h eK r i g i n g mo d e l 最大化获取修正空间内信息．常用的试验设计方法６２第９期陈奕丰等:基于K r i g i n g 模型的航空发动机管道系统有限元模型修正有正交设计㊁均匀设计㊁D 最优设计㊁中心复合设计抽样㊁拉丁超立方抽样等．之后基于训练样本拟合K r i g i n g 模型并检验模型精度直至符合精度要求．③针对目标函数的修正．在所拟合的K r i g i n g 模型的基础上,构建目标函数,之后引入如遗传算法㊁退火模拟算法㊁粒子群算法等优化算法对目标函数进行迭代处理,获取参数修正值．３．１㊀参数筛选与试验设计根据工程经验,初选结构中部分组件的材料参数和几何参数作为待修正参数．管道模型中选择的修正对象有导管密度㊁导管弹性模量㊁支座密度㊁支座弹性模量㊁外套螺母密度㊁外套螺母弹性模量等６个材料参数及导管内径㊁直通管接头长度㊁垫圈厚度㊁外套螺母长度等４个几何参数共１０个参数．基于斯皮尔曼(S pe a r m a n )等级相关系数[２２],分析各初选几何参数和材料参数对前５阶模态频率的灵表３㊀设计参数取值范围T a b l e ３㊀R a n g e o f d e s i gn p a r a m e t e r s D e s i gn p a r a m e t e r s I n i t i a lv a l u e L o w e rl i m i t U p pe r l i m i t P i p e l i n e d e n s i t y ρ１/(g c m －３)７．９３７．７７１８．０８９E l a s t i cm o d u l u s o f p i p e l i n e E １/G P a １９４１９０．１２０１９７．８８０S u p p o r t d e n s i t y ρ２/(g c m －３)２．８１２．７５４２．８６６E l a s t i cm o d u l u s o f s u p p o r t E ２/G P a ７１６９．５８０７２．４２０S l e e v en u t d e n s i t y ρ３/(g c m －３)４．５１４．４２０４．６００E l a s t i cm o d u l u s o f s l e e v e n u t E ３/G P a １１０１０７．８００１１２．２００I n n e r d i a m e t e r o f p i pe l i n e d /mm ４．８４．７０４４．８９６P i p e j o i n t l e n g t h L １/mm ４７４６．０６０４７．９４０W a s h e r t h i c k n e s s t /mm ２１．９６０２．０４S l e e v en u t l e n gt h L ２/mm １７１６．６６０１７．３４０图７㊀参数灵敏度分析F i g ．７㊀P a r a m e t e r s e n s i t i v i t y a n a l ys i s 敏度．选取显著性水平为０．０５,对各待修正参数设置上下２％的微小变化,如表３所示．计算前五阶频率对各参数的灵敏度,如图７所示．结合工程经验,剔除灵敏度相对较小的参数,选取导管内径d ㊁导管密度ρ１㊁导管弹性模量E １和支座弹性模量E ２四个参数作为待修正参数．试验设计方法采用拉丁超立方抽样方法,共选取了２５个样本点,如表４所示．拉丁超立方抽样是一种基于分层抽样思想的方法,将变量的概率分布函数分成数个互不重叠的等概率子区间,然后在每个子区间内进行独立随机采样,确保能在每个子区间内精确采样[２３]．表４㊀拉丁超立方抽样设计T a b l e ４㊀L a t i nh y p e r c u b e s a m p l i n g d e s i gn S a m pl eN o ．dρE １E ２１４．８００７．８０３１７６．９２８７０．４３２２４．９５４８．２４７２００．２０８６９．８６４３４．３３９７．９３０２０６．４１６６６．４５６４４．８７７８．６２８１９５．５５２６９．２９６５４．４１６７．４２２１８４．６８８７４．９７６６５．２２２８．１２０１８３．１３６７６．１１２７４．８３８８．３１１２０１．７６０７５．５４４８５．１８４７．５４９１９７．１０４７１．０００９４．６０８８．３７４１８６．２４０７３．８４０１０４．５３１７．４８６２１２．６２４７７．８１６１１４．６８５７．２９６１７５．３７６６４．７５２１２４．４９３８．５６４１９２．４４８７１．５６８１３４．７６１８．５０１１８７．７９２６８．１６０１４４．９９２７．７４０２０７．９６８６５．３２０１５４．６４６８．６９１１８１．５８４７６．６８０１６５．１０７７．６７６２０３．３１２６８．７２８１７５．０６９７．６１３１９０．８９６７７．２４８１８４．９１５７．９９３２０９．５２０６５．８８８１９４．４５４７．２３２１８９．３４４６７．０２４２０４．３７８８．１８４２１１．０７２６７．５９２２１４．７２３８．０５７１９８．６５６７４．４０８２２５．１４６８．４３８１７８．４８０６４．１８４２３５．２６１７．８６７２０４．８６４７２．１３６２４４．５７０７．３５９１８０．０３２７３．２７２２５５．０３０７．１６９１９４．０００７２．７０４３．２㊀K r i g i n g 模型构造K r i g i n g 模型是一种基于随机过程的半参数化７２动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２３年第２１卷模型,由线性回归部分和非参数随机部分组成．对于一组给定的输入参数和输出响应X ＝[x １,x ２, ,x m ]T 和输出响应Y ＝[y １,y ２, ,y m ]T ,K r i g i n g 模型的数学形式可表示为y (x i )＝ðpl ＝１βl f l(x i )＋z (x i )＝f T(x i )β＋z (x i )(１)式中,f l (x i )是基函数,βl 是基函数系数,z (x i )为拟合偏差函数,是对模型局部偏差的近似,f (x i )＝[f １(x i ),f ２(x i ), ,f p (x i )]T 是关于样本x 的多项式向量,β＝[β１,β２, ,βp ]T是线性回归系数向量,z (x )服从正态分布N (０,σ２z)并具有非零协方差,其协方差表达式为C o v [z (x i ),z (x j )]＝σ２z R (２)式中,z (x i ),z (x j )为任意两个样本点x i 和x j 的局部偏差;R 是由R i j (x i ,x j )组成的相关函数矩阵．R i j (x i ,x j )是一种可选定的相关函数,表示任意两个样本点间的空间相关性．本文选取工程中常用的高斯函数作为相关函数,其形式如下R i j (x i ,x j )＝e x p －ðnk ＝１θk x ki －x k j２()(３)式中,x ki和x k j分别为样本点x i 和x j 的第k 个分量;n 为设计变量的数目;θk 为未知的相关系数,控制不同维度上的相关衰减率．在训练K r i g i n g 模型中的参数时,通常使用最大似然估计．样本点的似然函数可表示为:L ＝１(２πσ２z )m Re x p －(Y －F β)TR －１(Y －F β)２σ２z éëêêùûúú(４)式中R 是相关函数矩阵R 的行列式,F 为样本点处f (x )向量值组成的矩阵．β和σ２z 的最小二乘估计可以表示为β^＝(F TR －１F )－１F TR －１Y (５)σ^２z ＝[(Y －F β)T R －１(Y －F β)]/m (６)将β和σ２z 最小二乘估计代入样本点的似然函数,忽略常数项并取对数,即可得到最大似然函数的对数形式为－n ２l n (σ２z )－１２l n R (７)σ２z和R 均为θk 的函数,通过优化算法求得式(７)的最大值,即可确定θk 的值．对于任意待测点x ０,最终响应的最佳线性无偏预测结果可表示为y ^(x ０)＝f T (x ０)β^＋r T(x ０)R －１(Y －F β^)(８)式中r T (x ０)＝[R (x ０,x １),R (x ０,x ２), ,R (x ０,x n )]基于上述K r i g i n g 模型理论,采用表４所示的拉丁超立方设计中的样本,拟合管道模型模态频率与四个设计变量之间的函数关系,绘制K ri g i n g 响应曲面,部分结果如图８所示．图８㊀模态频率响应曲面图F i g ．８㊀R e s p o n s e d i a g r a mo fm o d a l f r e qu e n c i e s ３．３㊀K r i g i n g 模型拟合精度分析为确定该模型能否代替有限元模型进行后续结构响应值的计算分析,对K r i g i n g 模型进行精度校验．常用的精度校验评价指标有:决定系数R ２㊁修正可决系数R ２a d j ㊁均方根误差R M S E 等[２４]．本文选用决定系数和均方根误差R M S E 两种检验标准,如式(９)和式(１０)所示．R ２＝１－ðKi ＝１(y i－y ^i )２ðKi ＝１(y i－y －)２(９)R M S E ＝１K y－ðKi ＝１(yi －y ^i )２(１０)式中,y i 为设计点处有限元计算值;y ^i 为响应面计算值;y －为有限元计算结果的平均值,K 为样本点总数．R ２ң１．表明代理模型与原模型相似度高,R M S E ң０表示代理模型误差小．K r i g i n g 模型精度检验结果如表５所示．结果显示前五阶决定系数均为１且R M S E 都接近于０,这表明所拟合的K r i gＧi n g 代理模型误差小㊁拟合精度高,可以作为原有限８２第９期陈奕丰等:基于K r i g i n g 模型的航空发动机管道系统有限元模型修正元模型的替代模型．表５㊀模态频率决定系数和均方根误差T a b l e ５㊀D e t e r m i n a t i o n c o e f f i c i e n t a n d r o o tm e a ns q u a r e e r r o r o fm o d a l f r e qu e n c i e s M o d e R ２RM S E１１３．０４E －０９２１１．６２E －０８３１１．０９E －０８４１２．７４E －０８５１１．１３E －０７３．４㊀模型修正及结果分析本文以修正后的管道模型有限元模型与实际管道模型响应尽可能接近为总体目标,利用模态试验所得模态频率构建的目标函数为m i n F (x )＝ðmi ＝１f ~i －f i f~i æèçöø÷２㊀s ．t ．㊀xjl o wɤx jɤx ju p ㊀(j ＝１,２,．．．,n )(１１)式中,f ~i 为第i 阶实测模态频率;f i 为第i 阶计算模态频率;x j 为第j 阶修正参数,x j l o w 和x ju p 为修正参数的最小值和最大值;m 为参与修正的样本个数;n 为修正参数的个数．基于拟合的K r i g i n g 模型,本文选用MO G A 遗传算法对目标函数进行求解优化．MO G A 遗传算法是基于受控精英主义策略的快速非支配排序遗传算法(N S G A ＧⅡ)[２５]的变体,它可以允许多个目标和约束,能获得分布均匀且兼具多样性的P a Ｇr e t o 解集．基于MO G A 遗传算法进行优化求解,最初生成４０００个样本,每次迭代生成８００个样本,并在最多２０次迭代中筛选出３个数据较好的样本点,在６９３７次评估后收敛,得到最终的K r i gＧi n g 模型修正结果．为验证本文模型修正方法的修正精度和修正效率,将K r i g i n g 模型修正方法与传统模型修正方法灵敏度方法进行对比,两种方法获得的管道模型修正前后的结构参数和模态频率的结果分别如表６和表７所示．表６㊀管道模型修正前后结构参数表T a b l e ６㊀C o m p a r i s o no f t h e p i p e l i n e s t r u c t u r a l p a r a m e t e r sb e f o r e a n da f t e rm o d e l u p d a t i n gP a r a m e t e rI n i t i a l v a l u eU p d a t e dm o d e l b a s e d U pd a te dv a l u e o nK r i g i n g mo d e l E r r o r /％U p d a t e dm o d e l b a s e d U pd a te dv a l u e o ns e n s i t i v i t y a n a l ys i s E r r o r /％d ４．８４．７７００．６２４．５７８４．８５ρ７．９３８．３９４５．８５８．１８８３．１５E １１９４１８０．６９０６．８６１８２．０２８６．５８E ２７１６３．９１５９．９８６９．１０１２．７５表７㊀管道模型修正前后模态频率结果表T a b l e ７㊀C o m p a r i s o no f p i p e l i n em o d a l f r e q u e n c i e sb e f o r e a n da f t e rm o d e l u p d a t i n gM o d eN o ．T e s t r e s u l t s /H zO r i gi n a lm o d e l F r e qu e n c i e s /H z E r r o r /％U p d a t e dm o d e l b a s e d F r e q u e n c i e s /H z o nK r i g i n g m o d e l E r r o r /％U p d a t e dm o d e l b a s e d F r e qu e n c i e s /H z o n s e n s i t i v i t y a n a l ys i s E r r o r /％１１２８．７６１３６．４３５．９６１２７．５４０．９６１２７．４０１．０６２２１８．６２２３１．０３５．６８２１８．５５０．０３２２４．３６２．５６３４０９．３７４３４．４４６．１２４１１．５４０．５３４１４．５８１．２６４６５１．５６６９６．６４６．９２６５１．５４０．００６５１．４９０．０１５１０４９．７６１１４０．００８．６０１０６５．０５１．４３１０６９．１８１．８２㊀㊀从表中可以发现:(１)通过灵敏度方法和K r i g i n g 模型修正方法修正后,管道各参数修正率较为接近,可以相互证实所提修正方法的可行性．(２)采用K r i g i n g 模型修正方法,修正前有限元模型与试验值之间各阶误差均超过工程允许的５％的误差范围,修正后将有限元模型误差同修正前原始误差相比,最大误差由８．６０％变为１．４３％,各阶相对误差均在５％以内,已满足工程实际的计算需求．(３)灵敏度分析方法得到的最大相对误差达到２．５６％,修正精度略逊于K r i g i n g 模型．同时,在同一系统上进行计算时,采用灵敏度分析方法进行修正需耗时２h ,而采用K r i g i n g 模型进行修正只需５m i n ,可９２动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２３年第２１卷见K r i g i n g 模型在计算效率方面具有显著的优越性．图９给出了重点修正的模态阶次所对应的模态振型．从结果中可以看出,通过K r i g i n g 模型修正后的有限元计算振型与实测振型具有较好的一致性,进一步说明了采用K r i g i n g 模型修正方法对管道结构进行有限元模型修正的适用性．图９㊀修正后模态振型与试验模态振型F i g ．９㊀U p d a t e dm o d e s h a p e s a n d t e s tm o d e s h a pe s ４㊀结论本文以某航空发动机管道模型为研究对象,采用力锤法进行了结构的模态试验并得出模态参数,通过A N S Y S 有限元分析软件建立有限元模型并进行模态分析,对比实测模态数据与有限元分析结果以确定有限元模型的精确度．结合工程经验与灵敏度分析方法筛选出待修正参数,采用拉丁超立方抽样设计进行试验设计,拟合出模态频率与结构参数之间的K r i g i n g 模型,利用MO G A 遗传算法完成了有限元模型修正．根据模态试验与有限元模型修正的结果,可得出以下结论:(１)通过对管道模型的模态试验结果进行分析,得到了管道模型的模态参数．其中,管道振型中端部有较大位移,管接头连接组件和支座对模态参数有较大影响,建模时应予以保留．(２)利用K r i g i n g 模型代替复杂的管道有限元模型进行有限元模型修正可以明显提高计算精度和效率．同修正前的有限元模型相比,所得各阶模态频率最大误差由８．６０％降为１．６３％,各阶相对误差均在５％以内,满足工程实际的计算需求．(３)对于管道结构,K r i g i n g 模型修正方法同灵敏度分析方法相比具有更高的修正精度和修正效率．灵敏度分析方法最大误差为２．５６％,K r i g i n g 模型修正方法最大误差为１．４３％,K r i g i n g 模型修正方法修正精度优于灵敏度分析方法．修正后的有限元模型能起到更好的预测效果,可为此类管系结构模型修正提供参考．参考文献[１]汪博,高培鑫,马辉,等．航空发动机管路系统动力学特性综述[J ]．航空学报,２０２２,４３(２):０２５３３２．WA N GB ,G A OPX ,MA H ,e t a l ．D yn a m i c c h a r Ｇa c t e r i s t i c so fa e r o Ｇe n g i n e p i p e l i n e s y s t e m :r e v i e w [J ]．A c t aA e r o n a u t i c a e tA s t r o n a u t i c aS i n i c a ,２０２２,４３(２):０２５３３２．(i nC h i n e s e)[２]张宇飞,王昊．基础激励作用下悬臂输流管的振动实验研究[J ]．动力学与控制学报,２０２２,２０(３):５０－５５．Z HA N G YF ,WA N G H．E x p e r i m e n t a l s t u d y on v i Ｇb r a t i o no f c a n t i l e v e r p i p e c o n v e y i n g fl u i du n d e r f u n Ｇd a m e n t a le x c i t a t i o n [J ]．J o u r n a lo f D yn a m i c sa n d C o n t r o l ,２０２２,２０(３):５０－５５．(i nC h i n e s e )[３]张皓,李东升,李宏男．有限元模型修正研究进展:从线性到非线性[J ]．力学进展,２０１９,４９:５４２－５７５．Z HA N G H ,L I DS ,L IH N．R e c e n t p r o gr e s s o n f i Ｇn i t e e l e m e n tm o d e l u p d a t i n g :f r o ml i n e a r i t y ton o n Ｇl i n e a r i t y [J ]．A d v a n c e s i n M e c h a n i c s ,２０１９,４９:５４２－５７５．(i nC h i n e s e)[４]屈美娇,陈果．一种航空发动机整机振动模型支承刚度的辨识方法[J ]．振动工程学报,２０１９,３２(３):４９０－５００．Q U M J ,C H E N G．As u p po r t s t i f f n e s s i d e n t i f i c a Ｇt i o n m e t h o df o rw h o l ea e r o Ｇe n g i n ev i b r a t i o n m o d e l [J ]．J o u r n a l o fV i b r a t i o nE n g i n e e r i n g ,２０１９,３２(３):４９０－５００．(i nC h i n e s e)[５]HA N Z H ,Z I MM E R MA N N ,G O R T ZS ．A l t e r n a Ｇt i v ec o k r i g i n g m o d e lf o rv a r i a b l e Ｇf i d e l i t y s u r r o g a t e m o d e l i n g [J ]．A I A AJ o u r n a l ,２０１２,５０(５):１２０５－０３第９期陈奕丰等:基于K r i g i n g模型的航空发动机管道系统有限元模型修正１２１０．[６]HA N Z H,G O R T ZS．H i e r a r c h i c a lk r i g i n g m o d e lf o r v a r i a b l eＧf i d e l i t y s u r r og a t e m o d e l i n g[J]．A I A AJ o u r n a l,２０１３,５０(９):１８８５－１８９６．[７]D I N G YJ,WA N G ZC,C H E N G,e t a l．M a r k o vC h a i n m o n t ec a r l oＧb a s e db a y e s i a n m e t h o df o rn o nＧl i n e a rs t o c h a s t i c m o d e l u p d a t i n g[J]．J o u r n a lo fS o u n da n dV i b r a t i o n,２０１９,５２０:１１６５９５．[８]秦仙蓉,潘杰,徐俭,等．塔式起重机结构有限元模型修正的响应面方法[J]．振动与冲击,２０１８,３７(６):２４４－２５０．Q I N X R,P A NJ,X U J,e ta l．R e s p o n s es u r f a c em e t h o d f o r t h e s t r u c t u r a l f i n i t e e l e m e n tm o d e l u p d aＧt i n g o f t o w e rc r a n e s[J]．J o u r n a lo fV i b r a t i o na n dS h o c k,２０１８,３７(６):２４４－２５０．(i nC h i n e s e) [９]张亚峰,彭珍瑞,张雪萍,等．基于径向基模型和巴氏距离的随机有限元模型修正[J]．振动与冲击,２０２１,４０(１９):２２１－２２９＋２７６．Z HA N G YF,P E N GZR,Z HA N GXP,e t a l．S t oＧc h a s t i c f i n i t e e l e m e n tm ode l u p d a t i n g b a s e d o n r a d i a lb a s i sm o d e l a n dB h a t t ac h a r y y ad i s t a n c e[J]．J o u r n a lo fV i b r a t i o na n dS h o c k,２０２１,４０(１９):２２１－２２９＋２７６．(i nC h i n e s e)[１０]D E N GZ M,G U OZP,Z HA N GXJ．I n t e r v a lm o dＧe l u p d a t i n g u s i n gp e r t u r b a t i o nm e t h o d a n d r a d i a l b aＧs i s f u n c t i o nn e u r a ln e t w o r k s[J]．M e c h a n i c a lS y sＧt e m s a n dS i g n a l P r o c e s s i n g,２０１７,８４:６９９－７１６．[１１]Z HA N G J,A U F T K,Y A N G D．F i n i t ee l e m e n t m o d e l u p d a t i n g o f l o n gＧs p a nc a b l eＧs t a y e db r i d g eb yK r i g i n g s u r r o g a t em o d e l[J]．S t r u c t u r a l E n g i n e e r i n ga n d M e c h a n i c s,２０２０,７４(２):１５７－１７３．[１２]张建侠,宋明顺,方兴华,等．基于K r i g i n g模型的多目标代理优化算法及其收敛性评估[J]．计算机集成制造系统,２０２１,２７(７):２０３５－２０４４．Z HA N GJX,S O N G MS,F A N GX H,e t a l．K r i gＧi n gＧa s s i s t e d m u l t iＧo b j e c t i v e o p t i m i z a t i o n a l g o r i t h ma n d i t s c o n v e r g e n c e a s s e s s m e n t[J]．C o m p u t e r I n t eＧg r a t e d M a n u f a c t u r i n g S y s t e m s,２０２１,２７(７):２０３５－２０４４．(i nC h i n e s e)[１３]WA N GJT,WA N GCJ,Z HA OJ P．F r e q u e n c y r eＧs p o n s e f u n c t i o nＧb a s e dm o d e l u p d a t i n g u s i n g K r i g i n gm o d e l[J]．M e c h a n i c a l S y s t e m sa n dS i g n a lP r o c e s sＧi n g,２０１７,８７:２１８－２２８．[１４]韩忠华．K r i g i n g模型及代理优化算法研究进展[J]．航空学报,２０１６,３７(１１):３１９７－３２２５．HA NZ H．K r i g i n g s u r r o g a t em o d e l a n d i t s a p p l i c aＧt i o n t od e s i g no p t i m i z a t i o n:ar e v i e wo f r e c e n t p r oＧg r e s s[J]．A c t aA e r o n a u t i c ae tA s t r o n a u t i c aS i n i c a,２０１６,３７(１１):３１９７－３２２５．(i nC h i n e s e)[１５]王文竹,李杰,刘刚,等．基于K r i g i n g代理模型鼓式制动器稳定性的优化设计[J]．振动与冲击,２０２１,４０(１１):１３４－１３８＋１６２．WA N G W Z,L I J,L I U G,e t a l．O p t i m i z a t i o nd eＧs i g no f d r u mb r a k e s t a b i l i t y b a s e do nK r i g i n g s u r r oＧg a t e m o d e l[J]．J o u r n a lo f V i b r a t i o na n d S h o c k,２０２１,４０(１１):１３４－１３８＋１６２．(i nC h i n e s e) [１６]张文鑫,吕震宙．一种新的自适应K r i g i n g法停止准则及其在涡轮盘疲劳寿命可靠性中的应用[J]．机械工程学报,２０２２,５８(６):２６３－２７３．Z HA N G W X,L V Z Y．N e ws t o p p i n g c r i t e r i o no fa d a p t i v eK r i g i n g m e t h o da n di t sa p p l i c a t i o ni nf aＧt i g u e l i f e r e l i a b i l i t y f o r t u r b i n ed i s k[J]．J o u r n a lo fM e c h a n i c a l E n g i n e e r i n g．２０２２,５８(６):２６３－２７３．(i nC h i n e s e)[１７]C U IQL,L I N G Y,C A O DS,e t a l．T h e r m a l d eＧs i g n p a r a m e t e r sa n a l y s i sa n d m o d e lu p d a t i n g u s i n gK r i g i n g m o d e l f o rs p a c ei n s t r u m e n t s[J]．I n t e r n aＧt i o n a lJ o u r n a l o f T h e r m a l S c i e n c e s,２０２２,１７１:１０７２３９．[１８]Y I N H,MAJ J,D O N GKL,e t a l．M o d e l u p d a t i n g m e t h o db a s e do n K r i g i n g m o d e l f o rs t r u c t u r a ld yＧn a m i c s[J]．S h o c k a n d V i b r a t i o n,２０１９,２０１９:８０８６０２４．[１９]李星占,董兴建,岳晓斌,等．振动响应传递率的动力学特性研究及其在工作模态分析中的应用[J]．振动与冲击,２０１９,３８(９):６２－７０．L IX Z,D O N G X J,Y U E X B,e ta l．D y n a m i cc h a r a c t e r i s t i c so fv i b r a t i o nr e s p o n s e t r a n s m i s s i b i l i t ya n d i t s a p p l i c a t i o n i no p e r a t i o n a lm o d a l a n a l y s i s[J]．J o u r n a l o fV i b r a t i o na n dS h o c k,２０１９,３８(９):６２－７０．(i nC h i n e s e)[２０]P E E T E R SB,A U W E R A E R H VD,G U I L L A U M EP,e t a l．T h e P o l y MA Xf r e q u e n c y d o m a i n m e t h o d:an e ws t a n d a r df o r m o d a l p a r a m e t e re s t i m a t i o n[J]．S h o c ka n dV i b r a t i o n,２００４(１１):３９５－４０９．[２１]沈旻昊．飞机液压管路的简化建模及振动特性分析[D]．西安:西安电子科技大学,２０１４:１５－１８．S H E N M H．S i m p l i f i e dm o d e l i n g a n d v i b r a t i o n a n a lＧy s i s o f t h ea i r c r a f th y d r a u l i c p i p e l i n e[D]．X i a n:X i d i a nU n i v e r s i t y,２０１４:１５－１８．(i nC h i n e s e) [２２]王逸龙,李晶,赵雪梅,等．基于优化设计的印制板组件精细化动力学建模方法[J]．动力学与控制学报,２０１７,１５(６):５１８－５２４．WA N G YL,L I J,Z HA OX M,e t a l．Ar e f i n e d a pＧ１３动㊀力㊀学㊀与㊀控㊀制㊀学㊀报２０２３年第２１卷p r o a c hf o rd y n a m i c m o d e l i n g o fa p r i n t e dc i r c u i t e db o a r da s s e m b l y b a s e do no p t i m i z a t i o nd e s i g n[J]．J o u r n a l o fD y n a m i c s a n dC o n t r o l,２０１７,１５(６):５１８－５２４．(i nC h i n e s e)[２３]万华平,任伟新,王宁波．高斯过程模型的全局灵敏度分析的参数选择及采样方法[J]．振动工程学报,２０１５,２８(５):７１４－７２０．WA N H P,R E N W X,WA N G N B．A G a u s s i a np r o c e s s m o d e lb a s e d g l o b a ls e n s i t i v i t y a n a l y s i sa pＧp r o a c hf o r p a r a m e t e rs e l e c t i o na n ds a m p l i n g[J]．J o u r n a l o fV i b r a t i o nE n g i n e e r i n g,２０１５,２８(５):７１４－７２０．(i nC h i n e s e)[２４]J I N Y．Ac o m p r e h e n s i v es u r v e y o f f i t n e s sa p p r o x iＧm a t i o n i ne v o l u t i o n a r y c o m p u t a t i o n[J]．S o f tC o mＧp u t i n g,２００５,９(１):３－１２．[２５]彭涛,田仲初,张建仁,等．基于多目标优化的混凝土斜拉桥静动力有限元模型修正[J]．振动与冲击,２０１８,３７(２１):１０８－１１６．P E N GT,T I A NZC,Z HA N GJR,e t a l．S t a t i c a n dd y n a m i c f i n i te e l e m e n tm o d e l u p d a t i n gf o r a c o n c r e t ec a b l eＧs t a y e db r id g eb a se do n m u l t iＧo b j e c t i v eo p t i m iＧz a t i o n[J]．J o u r n a lo fV i b r a t i o na n dS h o c k,２０１８,３７(２１):１０８－１１６．(i nC h i n e s e)２３。

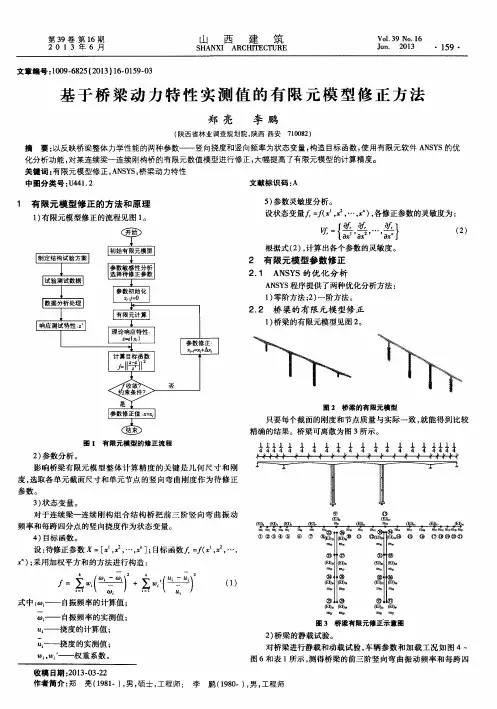
基于子结构的有限元模型修正方法翁顺;左越;朱宏平;陈波;赵会贤;田炜;颜永逸【期刊名称】《振动与冲击》【年(卷),期】2017(036)004【摘要】提出了一种基于子结构的有限元模型修正方法。

该方法将整体结构有限元模型划分为多个子结构模型，求解独立子结构的主模态特征解和特征灵敏度；通过位移协调条件和能量方程，约束相邻独立子结构，得到整体结构的特征解和特征灵敏度；并以整体结构模态和结构试验模态的残差为目标函数，通过调整子结构单元参数，完成有限元模型修正。

当结构局部参数发生变化，通过分析某一个或几个子结构即可求解整体结构特征解和特征灵敏度，而不需要分析其他未发生变化的子结构。

由于子结构模型尺寸远小于整体结构，该方法能够极大地提高有限元模型修正方法的精度和效率。

【总页数】7页(P99-104,138)【作者】翁顺;左越;朱宏平;陈波;赵会贤;田炜;颜永逸【作者单位】华中科技大学土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074;华中科技大学土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074;华中科技大学土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074;武汉理工大学土木工程与建筑学院，武汉 430070;华中科技大学土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074;华中科技大学土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074;华中科技大学土木工程与力学学院，控制结构湖北省重点实验室，武汉 430074【正文语种】中文【中图分类】TH212;TH213.3【相关文献】1.基于环境振动和贝叶斯定理的有限元模型自动修正方法及应用 [J], LIU Pei; ZHU Haixin; LIAN Pengyu; YANG Weiguo2.基于响应面的波形钢腹板PC组合梁桥有限元模型修正方法的试验研究 [J], 康志锐;张巍;宋帅;张进标3.基于MPGA算法的钢-混叠合梁有限元模型修正方法研究 [J], 孙浩4.基于子结构的大型桥梁有限元模型修正方法 [J], 宋晓东;颜永逸;李佳靖;翁顺;秦顺全5.基于模态参数及BAS-PSO优化算法的软基水闸有限元模型参数修正方法 [J], 李火坤;王刚;余杰;魏博文;黄伟;黄锦林因版权原因，仅展示原文概要，查看原文内容请购买。