五羊杯初中数学竞赛初三试题的研究.docx

环顾四周看蘑菇成堆生长——一个性质的再探究程奇;刘晓婷【期刊名称】《中学数学》【年(卷),期】2017(000)020【总页数】3页(P95-97)【作者】程奇;刘晓婷【作者单位】陕西富平县实验中学;陕西富平县实验中学【正文语种】中文在一次听课中，授课的老师讲解如下一道数学题，点P为等边△ABC内一点，求证点P到三边的距离和等于等边△ABC的高.讲授者利用面积法很快得到了答案，而笔者认为此题应从源头上进行探究，从而让学生在解题过程中通一知十，举一反三，从而跳出题设，理清整个解题思维过程，将“解题成果扩大”，故笔者建议从根题进行一一拓展.命题：等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.已知：如图1，在△ABC中，AB=AC，点P是边BC上任意一点，过点P作PE⊥AB，PF⊥AC，垂足分别是E、F，过点C作CH⊥AC，垂足为H.求证：PE+PF=CH.证法1：面积法.证明：连接AP.方法总结：证法1利用面积分割法解决线段间的和差问题，面积分割法实际上就是把一个图形分成几个图形，根据面积相等找到等量关系，这种方法在解题中有着广泛的应用.在解决线段之间和差关系时，我们还可以用截长法或补短法来解决. 证法2：截长法.分析：运用截长法辅助线的作法较多，如（1）过点P作PG∥EH交CH于点G，易得四边形HEPG为矩形，可证明Rt△CGP≌Rt△PFC，从而得出CG=PF，得出结论；（2）在CH上截取HG=EP或CG=PF，以下以该法为例说明；（3）过点P 作PG⊥CH，垂足为G，易得四边形HEPG为矩形，易得结论.证明：如图2，在CH上截取HG=EP，连接PG.易得四边形EPGH是矩形.则∠HGP=90°，GP∥HE.则∠GPC=∠B.由AB=AC，得∠B=∠ACB.则∠GPC=∠ACB.又PC=CP，∠PGC=∠CFP=90°，则△CGP≌△PFC（AAS）.则PF=CG.则PE+PF=HG+CG=CH.证法3：补短法.分析：运用此方法辅助线作法较多：（1）如图3，延长AB至点D，使BD=EH，过点D作DG∥BC，交EP的延长线于点G（平移△HCB），易得四边形HEGC为矩形，再证明△CGP≌△CFP，易得结论；（2）如图4，延长EP至点G，使EG=HC，连接CG，以下证法以（2）为例.证明：如图4，延长EP至点G，使EG=HC，连接CG.易得四边形HEGC是矩形.则∠G=90°，GC∥HE.由AB=AC，得∠B=∠ACB.由GC∥HE，得∠GCP=∠B.则∠ACB=∠GCP.又PC=PC，∠C=∠CFP=90°，则△CGP≌△CFP（AAS）.则PF=PG.则PE+PF=PE+PG=EG=CH.证法4：利用三角形相似.证明：由PE⊥AB，PF⊥AC，CH⊥AB，得∠BEP=∠BHC=∠CFP=90°.以下证法同证法4.证明2：由AB=AC，得∠B=∠FCP.由∠BEP=∠PFC=∠CHB=90°，得BP=PE÷sinB，BC=CH÷sinB，PC=PF÷sin∠FCP=PF÷sinB.又BP+PC=BC，则PE÷sinB+PF÷sinB=CH÷sinB.则PE+PF=CH.证法6：轴对称.分析：（1）如图5，作△A′BC使其与△ABC关于BC对称，延长EP交A′C于点F′，则四边形ABA′C是菱形，可得A′C∥AB，BC是∠ACB的平分线，从而得到PF′=PF，根据平行线间距离处处相等，易得结论；（2）如图6，作△PGC使其与△PFC关于PC对称，易得∠EPB=∠CPG，∠G=90°，从而得出∠EPG=180°，即点E、P、G在同一直线上，四边形EGCH是矩形，结论可得.当∠BAC是直角或钝角时，命题仍成立.（证明方法同上）拓展1：等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高. 即：如果点P在BC（或CB）的延长线上，如图7，有下列结论：|PE-PF|=CH.（证明方法同命题证明）拓展2：如果把等腰三角形改为等边三角形，又有如下结论：如图8，等边△ABC和点P，当点P在△ABC的一边BC上时，点P到△ABC的三边AB、AC、BC的距离分别为h1、h2、h3，△ABC的高为h，此时h3=0，则h1+h2+h3=h.（证明方法同命题证明）延伸1：当点P为△ABC内任意一点时，如图9，结论h1+h2+h3=h仍成立.延伸2：当点P为△ABC外任意一点时，如图10、图11，结论|h1+h2-h3|=h成立.（证明方法同命题证明）即：（1）等边三角形内任意一点到三边距离和等于这个三角形一边上的高；（2）等边三角形外任意一点到角两边的距离和与到第三边的距离的差的绝对值等于等边三角形的高.即：图10结论为h1+h2-h3=h；图11结论为h1+h2-h3=-h.拓展3：如果把等腰三角形改为等腰梯形，又有如下结论：如图12，等腰梯形ABCD中，AB∥CD，点P是上底AB或下底CD上任意一点，点P到腰AD、BC的距离分别为h1、h2，点D到腰BC的距离为h，则h1+h2=h.分析：可借助辅助线，延长两腰或平移一腰等方式构造等腰三角形，再利用命题结论可证得.即：等腰梯形上底（或下底）上任意一点到两腰的距离和等于该底边任一顶点到所对腰的距离拓展4：如果把等边三角形变为正方形、正五边形、…、正n边形，又有如下结论：若点P为正方形ABCD内任一点，点O为正方形的中心，点P到各边的距离分别为h1、h2、h3、h4，点O到一边的距离为r4，则h1+h2+h3+h4=4r4.若点P为正五边形ABCDE内任一点，点O为正五边形的中心，点P到各边的距离分别为h1、h2、h3、h4、h5，点O到一边的距离为r5，则h1+h2+h3+h4+h5=5r5.若点P为正n边形内任一点，O是正n边形的中心，点O到一边的距离为rn，点P到各边的距离分别为h1、h2、…、hn，则h1+h2+…+hn=nrn.证明方法同命题.例1 如图13，矩形ABCD中，AB=3，BC=4，P为AD边上任意一点，且PE⊥AC，PF⊥BD，垂足分别为E、F，则PE+PF的值为（）.例2 （全国初中数学竞赛）如图14，边长为1的正方形ABCD，∠ACE=22.5°，点P是CE上任意一点，PH⊥BD，PG⊥AC，垂足分别为H、G，求PH+PG.例3 （全国初中数学联赛试题）如图15，从等边三角形内一点向三边作垂线，已知三条垂线段的长分别为1、3、5，则这个等边三角形的边长为________.例4 （第八届“五羊杯”初中数学竞赛初三试题）如图16，等边△ABC外有一点P，点P落在∠ABC内，设点P到BC、CA、AB的距离分别是h1、h2和h3且满足h1-h2+h3=6，求等边△ABC的面积.例5 （数学竞赛试题改编）如图17，正八边形的边长为a，点P是八边形内任意一点，点P到八条边的距离分别为h1、h2、…、h8，求正八边形的面积.王金战老师的学习方法中指出：好问题同蘑菇相似，它们大都成堆地生长，要高效率地学好数学，不能就题论题，要力争“环顾四周”，看它们有没有“成堆生长”.这种方法不仅在教师教学探究中经常用到，更应将这种方法教授给学生，提高学生对知识的归纳能力并整合自己的知识体系.。

第五讲 有条件的分式的化简与求值给出一定的条件，在此条件下求分式的值称为有条件的分式求值．而分式的化简与求值是紧密相连的，求值之前必须先化简，化简的目的是为了求值，先化筒后求值是解有条件的分式的化简与求值的基本策略．解有条件的分式化简与求值问题时，既要瞄准目标．又要抓住条件，既要根据目标变换条件．又要依据条件来调整目标，除了要用到整式化简求值的知识方法外，还常常用到如下技巧:1．恰当引入参数；2．取倒数或利用倒数关系； 3．拆项变形或拆分变形； 4．整体代入；5．利用比例性质等． 例题求解 【例1】若a d d c cb b a ===，则dc b a dc b a +-+-+-的值是 ． (第12届“希望杯”邀请赛试题)思路点拨 引入参数，利用参数寻找a 、b 、c 、d 的关系． 注：解数学题是运用巳知条件去探求未知结论的一个过程．如何运用已知条件是解题顺畅的重要前提，对巳知条件的运用有下列途径： (1)直接运用条件； (2) 变形运用条件； (3) 综合运用条件； (4)挖掘隐含条件．在解某些含多个字母的代数式问题时，如果已知与未知之间的联系不明显，为了沟通已知与未知之间的联系，则可考虑引入一个参数，参数的引入，可起到沟通变元、消元的功能．【例2】如果11=+b a ，12=+c b ，那么ac 2+等于( ) A ．1 B ．2 C ．3 D ．4(2002年全国初中数学联赛武汉选拔赛) 思路点拨 把c 、a 用b 的代效式表示．【例3】已知1=xyz ，2=++z y x ，16222=++z y x ，求代数式yzx x yz z xy 212121+++++的值． (2003年北京市竞赛题)思路点拨 直接通分，显然较繁，由x+y+z=2，得z=2－x －y ，x=2－y －z ，z ＝2－x －y ，从变形分母入手．【例4】不等于0的三个数a 、b 、c 满足cb ac b a ++=++1111，求证a 、b 、c 中至少有两个互为相反数．(天津市竞赛题)思路点拨 要证a 、b 、c 中至少有两个互为相反数，即要证明(a+b)(b+c)(c+a)＝0，使证明的目标更加明确．【例5】 (1)已知实数a 满足a 2－a －1=0，求487-+a a 的值．(2003年河北省竞赛题) (2)汜知1325))()(())()((=+++---a c c b b a a c c b b a ，求ac cc b b b a a +++++的值． (“北京数学科普日”攻擂赛试题) 思路点拨 (1)由条件得a 2=a+1，11=-aa ，通过不断平方，把原式用较低的多项式表示是解题的关键．(2)已知条件是b a b a +-、cb c b +-、a c ac +-三个数的乘积，探求这三个数的和与这三个数的积之间的关系，从而求出b a b a +-+c b c b +-+ac ac +-的值是解本例的关键．学历训练1．已知032=-+x x ，那么1332---x x x = ． (2003年淄博市中考题)2．已知712=+-x x x ，则1242++x x x = ．3．若a 、b 、c 满足a+b +c=0，abc>0，且c c b b a a x ++=，y=)11()11()11(ba c a cbc b a +++++，则xy y x 32++= ． (“祖冲之杯”邀请赛试题) 4．已知43322a c c b b a -=-=+，则ba cb a 98765+-+= ．(第12届“五羊杯”竞赛题) 5．已知a 、b 、c 、d 都是正数，且d c b a <，给出下列4个不等式：①d c c b a a +>+；②dc cb a a +<+；③d c d b a b +>+；④ dc db a b +<+，其中正确的是( ) (2002年山东省竞赛题) A ．①③ B ．①④ C ．②④ D ．②③ 6．设a 、b 、c 是三个互不相同的正数，如果abb ac b c a =+=-，那么( ) A ． 3b=2c B ．3a=2b C ．2b=c D ．2a=b. (“祖冲之杯”邀请赛试题) 7．若4x —3y 一6z=0，x+2y －7z=0(xyz ≠0)，则代数式222222103225z y x z y x ---+的值等于( )．A ． 21-219- C ．－15 D ． －13. (2003年全国初中数学竞赛题) 8．设轮船在静水中速度为v ，该船在流水(速度为u <v )中从上游A 驶往下游B ，再返回A ，所用时间为T ，假设u =0，即河流改为静水，该船从A 至B 再返回B ，所用时间为t ， 则( )A ．T=tB ．T<tC ．T>tD ．不能确定T 、t 的大小关系9．(1)化简，求值：24)44122(22+-÷++--+-a a a a a a a a ，其中a 满足0122=-+a a ； (2002年山西省中考题)(2)设0=++c b a ，求abc c ac b b bc a a +++++222222222的值．10．已知xz z y y x 111+=+=+，其中x 、y 、z 互不相等，求证：x 2y 2z 2=1．11．若0≠abc ，且b ac a c b c b a +=+=+，则abca c cb b a ))()((+++= ． 12．已知a 、b 、c 满足1222=++c b a ，3)11()11()11(-=+++++ba c c abc b a ，那么 a+b+c 的值为 ． 13．已知1=+y x xy ，2=+z y yz ，3=+xz zx，则x 的值为 ． 14．已知x 、y 、z 满足41=+y x ，11=+z y ，371=+x z ，则xyz 的值为 ． (2003年全国初中数学竞赛题)15．设a 、b 、c 满足abc ≠0，且c b a =+，则abc b a ca b a c bc a c b 222222222222-++-++-+的值为A ．－1B ．1C ．2D ．3 (2003年南通市中考题) 16．已知abc=1，a+b+c=2，3222=++c b a ，则111111-++-++-+b ca a bc c ab 的值为( ) A ．－1 B ．21-C ．2D ．32- (大原市竞赛题) 17．已知—列数1a 、2a 、3a 、4a 、5a 、6a 、7a ，且1a =8，7a =5832，766554433221a a a a a a a a a a a a =====，则5a 为（ ） A ．648 B ． 832 C ．1168 D ．194418．已知0199152=--x x ，则代数式)2)(1(1)1()2(24----+-x x x x 的值为( )A ．1996B ．1997C ．1998D ．1999 19．（1）已知ac b =2，求)111(333333222cbacb ac b a ++⋅++的值；(2)已知x 、y 、z 满足1=+++++y x z x z y z y x ，求代数式yx z x z y z y x +++++222的值． (2002年北京市竞赛题)20．设a 、b 、c 满足c b a c b a ++=++1111，求证：当n 为奇数时，n n n n n n cb ac b a 1111++=++ (波兰竞赛题)21．已知012=--a a ，且1129322322324-=-++-axa a xa a ，求x 的值． (2000年上海市高中理科班招生试题)22．某企业有9个生产车间，现在每个车间原有的成品一样多，每个车间每天生产的成品也一样多，有A，B两组检验员，其中A组有8名检验员，他们先用2天将第一、第二两个车间的所有成品(指原有的和后来生产的)检验完毕后，再检验第三、四两个车间的所有成品，又用去了3天时间，同时，用这5天时间，B组检验员也检验完余下的5个车间的所有成品．如果每个检验员的检验速度一样快，每个车间原有的成品为a件，每个车间每天生产b件成品．(1)试用a、b表示B组检验员检验的成品总数；(2)求B组检验员的人数．(2001年天津市中考题) 答案：。

O
P
A
B
R Q
A B C D E P
A
B O
C
D M
N
A
O
B
R
Q
P
A
B
N
M
O
利用轴对称性解极值
1、(2001年“五羊杯”数学竞赛初三试题)如图，︒=∠45AOB ，角内有点P ，PO=10.在两边上有点Q 、R(均不同于O),则PQR ∆的周长的最小值为 .
2、（2001年“希望杯”数学初二试题）如图，在菱形ABCD 中，︒=∠120DAB ，点E 平分DC ，点P 在BD 上，且PE+PC=1，那么AB 的最大值 .
3、（中等数学）如图，︒=∠30AOB AOB ∠内有一点P ，且OP=10，在OA 上有一点Q ，OB 上有一点R ，若PQR ∆周长最小，则最小周长是 .
1P 2P
4、（97浙江中考题）如图，设︒=∠20MON ，A 为OM 上一点，OA=34，D 为ON 上一点，OD=38。

C 为AM 上任一点，B 是OD 上任意一点，那么折线ABCD 的长最小是多少？
5、（2000年湖北省荆门中考题）如图，A 点是半圆上一个三等分点，B 点是N A
的中点，P 点是直径MN 上一动点，已知⊙O 的半径为1，则AP+BP 的最小值为（ ） A 1 B 2
2
C 2
D 13-。

6.计算──工具与算法的变迁知识纵横研究数学、学习数学总离不开计算,随着时代的变迁,计算工具在不断在改变,•从中国古老的算盘、纸笔运算发展到利用计算器、计算机(computer)运算.初中代数中运算贯穿于始终,运算能力是运算技能与逻辑能力的结合,它体现在对算理算律的理解与使用,综合运算的能力及选择简捷合理的运算路径上,这要求我们要善于观察问题的结构特点,灵活选用算法和技巧,有理数的计算常用的方法与技巧有:1.巧用运算律;2.用字母代数;3.分解相约;4.裂项相消;5.利用公式等.例题求题【例1】现有四个有理数3,4,-6,10,将这4个数(每个数用且只用一次)进行加、减、乘、除四则运算,使其结果等于24,其三种本质不同的运算式有:(1)________________;(2)__________________;(3)____________________. (浙江省杭州市中考题)思路点拨从24最简单的不同表达式入手,逆推、拼凑.解:下列算式供参考:3×[4+10+(-6)],(10-4)-3×(-6),4-(-6)÷3×10.【例2】如果4个不同的正整数m、n、p、q满足(7-m)(7-n)(7-p)(7-q)=4,•那么m+n+p+q 等于( ).A.10B.21C.24D.26E.28(2001年新加坡数学竞赛题) 思路点拨解题的关键是把4表示成4个不同整数的形式.解:选E 提示:4=2×(-2)×1×(-1)【例3】计算:(1)1+112++1123+++…+1123100+++⋅⋅⋅+(“祖冲之杯”邀请赛试题)(2)19492-19502+19512-19522+…+19972-19982+19992; (北京市竞赛题)(3)5+52+53+ (52002)思路点拨对于(1),首先计算每个公分母值,则易掩盖问题的实质,不妨先从考察一般情形入手;(2)式使人易联想到平方差公式;对于(3),•由于相邻的后一项与前一项的比都是5,可从用字母表示和式着手.解:(1) 200101提示:1123n+++⋅⋅⋅+=1(1)2n n+=2(1)n n+=2(1n-11n+)(2)3897326;(3) 2003554- 提示:设s=5+52+53+...+52002,则5s=52+53+ (52003)【例4】(1)若按奇偶分类,则22004+32004+72004+92004是________数;(2)设a=355,b=444,c=533,则a 、b 、c 的大小关系是_______(用“>”号连接); (3)求证:32002+42002是5的倍数.思路点拨 乘方运算是一种特殊的乘法运算,•解与乘方运算有关问题常用到以下知识:①乘方意义;②乘方法则;③a 2n ≥0;④a n 与a 的奇偶性相同;⑤在n 4k+r 中(k,r 为非负整数,n ≠0,0≤r<4),当r=0时,n 4k+r 的个位数字与n 4的个位数字相同;当r ≠0时,n 4k+r •的个位数字与n r 的个位数字相同. 解:(1)奇;(2)a>b>c.(3)因为32002=34×500+2,42002=44×500+2,所以32002与42002的个位数字分别与32、42的个数数字相同,即9、6,•从而32002+42002的个位数字为5,因此,32002+42002是5的倍数.【例5】有人编了一个程序:从1开始,交替地做加法或乘法(第一次可以是加法,也可以是乘法),每次加法,将上次运算结果加2或加3;每次乘法,将上次运算结果乘2或乘3,例如,30可以这样得到:13+−−→42⨯−−→82+−−→103⨯−−→30.(1)证明:可以得到22;(2)证明:可以得到2100+297-2.思路点拨 要证明可以得到相应的数,只要编出符合要求的程序即可.解:(1)1 2⨯−−→ 2 2+−−→ 4 2⨯−−→ 8 2+−−→ 10 2⨯−−→ 20 2+−−→ 22; (2)1 2⨯−−→ 3×2-4 2+−−→ 3×2-2 2⨯−−→ 3×22-4 2+−−→ 3×22-22⨯−−→ 3×23-4 2+−−→ 3×23-2…(不断乘以2，再加2) 2⨯−−→3×296-43+−−→3×296-1 3⨯−−→ 299+296-3 2+−−→ 299+296-1 2⨯−−→ 2100+297-2.学力训练一、基础夯实1.(1)计算:211×(-455)+365×455-211×545+545×365=_________;(2)若a= -20042003,b=-20032002,c=-20022001,则a、b、c的大小关系是___________(用“〈”号连接〉.2.计算:(1)0.7×149+234×(-15)+0.7×59+14×(-15)=________;(第15届江苏省竞赛题)(2) 191919767676-76761919=________. (第12届“希望杯”邀请赛试题)(3)135⨯+157⨯+…+119971999⨯=________; (天津市竞赛题)(4)(13.672×125+136.72×12.25-1367.2×1.875)÷17.09=________.(第14届“五羊杯”竞赛题)3.在下式的每个方框内各填入一个四则运算符号(不再添加括号),•使得等式成立:6□3□2□12=24. (第17届江苏省竞赛题)4.1999加上它的12得到一个数,再加上所得的数的13又得到一个数,再加上这次得数的14又得到一个数,……,依此类推,一直加到上一次得数的11999,那么最后得到的数是_________.5.根据图所示的程序计算,若输入的x值为32,则输出的结果为( ).A.72B.94C.12D.92(2002年北京市海淀区中考题)y=-x+21<x≤2y=x2-1<x≤1y=x+2-2≤x≤-1输出y值输入x值6.已知a=-199919991999199819981998⨯-⨯+,b=-200020002000199919991999⨯-⨯+,c=-200120012001200020002000⨯-⨯+,则abc=( ).A.-1B.3C.-3D.1 (第11届“希望杯”邀请赛试题)7.如果有理数a 、b 、c 满足关系a<b<0<c,那么代数式23bc acab c 的值( ).A.必为正数B.必为负数C.可正可负D.可能为0 8.将322、414、910、810由大到小的排序是( ).A.322、910、810、414B.322、910、414、810C.910、810、414、322D.322、414、910、810 (美国犹他州竞赛题) 9.阅读下列一段话,并解决后面的问题:观察下面一列数:1,2,4,8,…,我们发现,这一列数从第2项起,•每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,•这一列数就叫做等比数列,这个常数叫做等比数列的公比. (1)等比数列5,-15,45,…的第4项是________;(2)如果一列数a 1,a 2,a 3,a 4,…是等比数列,且公比为q,那么根据上述的规定,有 •21a a =q, 32a a =q, 43aa =q,…, 所以a 2=a 1q,a 3=a 2q=(a 1q)q=a 1q 2,a 4=a 3q=a 1q 3,…,a n =_______(用a 1与q 的代数式表示). (3)一个等比数列的第2项是10,第3项是20,求它的第1项与第4项. (2003年广西省中考题)10.(1)已知a 、b 、c 都不等于零,且||a a +||b b +||c c +||abcabc 的最大值是m,最小值为n,求m n mn的值.(2)求证:5353-3333是10的倍数.二、能力拓展11.计算:(1) 2200340042003200240082003200422003300520032003200520053005-⨯+⨯-⨯-⨯-⨯+⨯=_________.(第15届“希望杯”邀请赛试题)(2)2-22-23-24-25-26-27-28-29+210=___________;(3) 123369510157142113539155152572135⨯⨯+⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯=_______________.(4)98+998+9998+…+5099998⋅⋅⋅个=_________.(2003年“信利杯”竞赛题) 12.(1)32001×72002×132003所得积的末位数字是________;(第17届江苏省竞赛题) 13.若a 、b 、c 、d 是互不相等的整数(a<b<c<d),且abcd=121,则a c +b d =________. 14.你能比较20012002与20022001的大小吗?为了解决这个问题,我们先写出它的一般形式,即比较n n+1与(n+1)n 的大小(n 是自然数),然后,我们从分析n=1,n=2,n=3,……中发现规律,经归纳、猜想得出结论. (1)通过计算,比较下列各组中两数的大小(在空格中填写“)”、“＝”、•“〈”号〉. ①12_____21; ②23______32; ③34______43; ④45______54; ⑤56_____65;…… (2)从第(1)题的结果经过归纳,可以猜想出n n+1和(n+1)n 的大小关系是_______.(3)根据上面归纳猜想得到的一般结论,试比较下列两个数的大小20012002___20022001. (江苏省常州市中考题) 15.如果11||t t +22||tt +33||t t =1,则123123||t t t t t t 的值为( ). A.-1 B.1 C.±1 D.不确定 (2003河北省竞赛题) 16.如果ac<0,那么下面的不等式ac<0,a c 2<0,a 2c<0,c 3a<0,ca 3<0中必定成立的有( • ). A.1个 B.2个 C.3个 D.4个17.设S=213⨯+2235⨯+3257⨯+…4929799⨯,T=13+25+227+…48299,则S-T=( ).A.49299B.1-49299C.49299-1D.49299+1 (第14届“五羊杯”竞赛题)18.10个互不相等的有理数,每9个的和都是“分母为22的既约真分数(分子与分母无公约数的真分数)”，则这10个有理数的和为( ). A.12 B. 1118 C. 76 D. 59(第11届江苏省竞赛题)19.图中显示的填数“魔方”只填了一部分,将下列9个数: 14,12,1,2,4,8,•16,•32,64填入方格中,使得所有行、列及对角线上各数相乘的积相等,求x的值. (上海市竞赛题)64x3220.设三个互不相等的有理数,既可分别表示为1,a+b,a的形式,又可分别表示为0, ab,b的形式,求a2002+b2001的值.三、综合创新21.(1)三个2,不用运算符号,写出尽可能大的数;(2)三个4,不用运算符号,写出尽可能大的数.(3)用相同的3个数字(1～9),不用运算符号,写出最大的数.22.如图,是一个计算装置示意图,J1、J2是数据输入口,C是计算输出口,计算过程是由J1、J2分别输入自然数m和n,经计算后得自然数K由C输出,此种计算装置完成的计算满足以下三个性质:(1)若J1、J=2分别输入1，则输出结果为1;(2)若J=1输入任何固定的自然数不变,J2输入自然数增大1,则输出结果比原来增大2;(3)若J2输入1,J1输入自然数增大1,则输出结果为原来的2倍.试问:(1)若J1输入1,J2输入自然数n,输出结果为多少?(2)若J2输入1,J1输入自然数m,输出结果为多少?(3)若J1输入自然数m,J2输入自然数n,输出的结果为多少?(2002年扬州中学招生试题)C nmj2 j1答案：1.(1)154000,(2)a>b>c.2.(1)-43.6;(2)-334;(3) 9985997; (4)•48,•注意13672=•8•×1709. 3.略 4.1999000 提示:原式=1999×(1+12)(1+13)×…×(1+11999) 5.C 6.A 7.B 8.A 9.(1)-135;(2)a n =a 1q n-1;(3)a 1=5,a 4=40. 10.(1)-16 提示:||xx =±1,m=4,n=-4;(2)5353与3333的个位数字相同. 11.(1)667668;(2)6 提示:2n+1-2n =2n ;(3)25; (4) 111000491⋅⋅⋅ 个 12.(1)9;(2)115200 13.-1214.(1)略;(2)当n<3时,n n+1<(n+1)n ;当n ≥3时,n n+1>(n+1)n ;(3)>. 15.A 16.C 17.B 提示:1111()(2)22n n n n =-++ 18.A 19.这9个数的积为14×12×1×2×4×8×16×32×64=643, 所以,每行、每列、每条对角线上三个数字积为64, 得ac=1,ef=1,ax=2,a,c,e,f 分别为14,12, 2,4中的某个数,推得x=8. fed c b a 64x 3220.2 提示:这两个三数组在适当的顺序下对应相等,于是可以断定,a+b 与a•中有一个为0,ba与b 中有一个为1,再讨论得a=-1,b=1. 21.(1)222;(2)444=4256>444;(3)设所用数字为a,可得下面4种写法:①当a=1时,111最大;②当a=2时,222最大;③当a=3时,333最大;④当a ≥4时,a 最大. 22.由题意设输出数,设C(m,n)为k,则C(1,1)=1,C(m,n)=c(m,n-1)+2,C(m,•1)•=2C(m-1,1).(1)C(1,n)=C(1,n-1)+2=C(1,n-2)+2×2=…= C(1,1)+2(n-1)=1+2(n-1)=2n-1 (2)C(m,1)=2C(m-1,1)=22·C(m-2,1)=…=2m-1C(1,1)=2m-1.(3)C(m,n)=C(m,n-1)+2=C(m,n-2)+2×2=…=C(m-1)+2(n-1)=22C(m-2,1)+2(n-1)=…=2m-1C(1,1)+2n-2=2m-1+2n-2.。

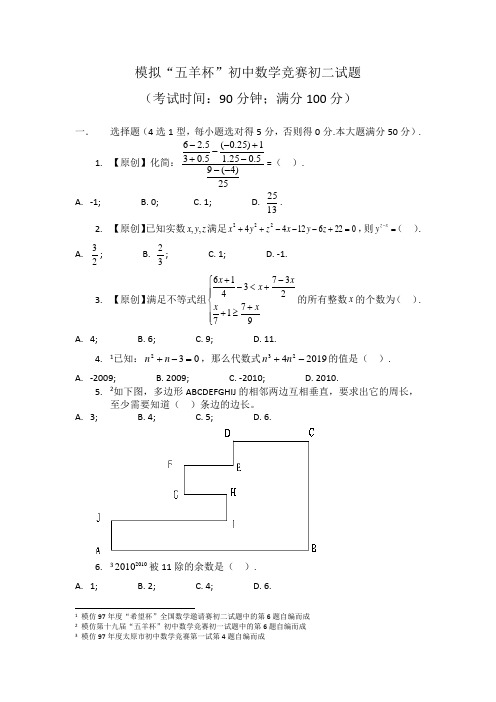
模拟“五羊杯”初中数学竞赛初二试题（考试时间：90分钟；满分100分）一． 选择题（4选1型，每小题选对得5分，否则得0分.本大题满分50分）.1. 【原创】化简：25)4(95.025.11)25.0(5.035.26---+--+-=（ ）. A. -1; B. 0; C. 1; D. 1325. 2. 【原创】已知实数z y x ,,满足022********=+---++z y x z y x ，则=-x z y （ ）.A. 23;B. 32; C. 1; D. -1. 3. 【原创】满足不等式组⎪⎪⎩⎪⎪⎨⎧+≥+-+<-+97172373416x x x x x 的所有整数x 的个数为（ ）. A. 4; B. 6; C. 9; D. 11.4. 1已知：032=-+n n ，那么代数式2019423-+n n 的值是（ ）.A. -2009;B. 2009;C. -2010;D. 2010.5. 2如下图，多边形ABCDEFGHIJ 的相邻两边互相垂直，要求出它的周长，至少需要知道（ ）条边的边长。

A. 3;B. 4;C. 5;D. 6.6. 320102010被11除的余数是（ ）.A. 1;B. 2;C. 4;D. 6. 1模仿97年度“希望杯”全国数学邀请赛初二试题中的第6题自编而成 2 模仿第十九届“五羊杯”初中数学竞赛初一试题中的第6题自编而成 3 模仿97年度太原市初中数学竞赛第一试第4题自编而成7. 4设1233+--=Θb a ab b a ，b a ,是任意实数，则=ΘΘΘΘΘΘΘ)11451041937833()10003100310313(（ ）. A. 3101510+⨯; B. 101015⨯; C. 310159+⨯; D. 91015⨯.8. 5如果c b a <<，z y x <<，且0,,≠z y x ，那么在四个代数式：①zc y b x a ++； ②y c z b x a ++；③z c x b y a ++；④y c x b z a ++中，哪一个的值最小？（ ） A. ①； B. ②； C. ③； D. ④.9. 6打字员小张连续打字20分钟，打了3609个字符，已测得他在第一分钟打了120个字符，在最后一分钟打了98个字符. 如果测算他每一分钟所打字符的个数，则以下结论不成立的是（ ）.A. 必有连续2分钟打了至少377个字符；B. 必有连续3分钟打了至少566个字符；C. 必有连续6分钟打了至少1131个字符；D. 必有连续9分钟打了至少1697个字符.10. 7空间中八个点（任意三点不共线）两两连线，用红绿两色染这些线段，其中点A 连出的线段都是红色的. 那么，以这八个点为顶点的三角形中，三边同色的三角形的个数至少为（ ）.A. 13；B. 14；C. 15；D. 16.二． 填空题（每小题填对得5分，否则得0分.本大题满分50分）.1. 8已知p 是质数，并且37+p 也是质数，则=-3811p _______. 2. 【原创】设9位自然数m=______________2201091xy ，m 是88的倍数，则m=_______. 3. 9某校初二三个班同学举行羽毛球混合双打表演，要求每班都派出一名男生和一名女生，规定同班的男女生不能配对.如果派出的男生分别是甲、乙、丙、丁，派出的女生分别是A 、B 、C 、D.第一场：甲和A 对丙和C ；第二场：丙和B 对甲和C ；第三场：丁和A 对乙和丙的同班女生.那么，甲、乙、丙、丁的同班女生分别是__________. 4模仿第十九届“五羊杯”初中数学竞赛初二试题中的第8题自编而成 5 改编自《数学竞赛培训教程（初中册）第38页例2 6 改编自第十二届“五羊杯”初中数学竞赛初二试题第10题 7 改编自《中学数学》2010年5月数学奥林匹克初中训练题129第6题 8 改编自96年度北京市初中数学竞赛初二试题第1题 9 模仿98年度北京市初一年级“迎春杯”数学竞赛试题填空题第1题自编而成4.10某个两位数___ab ，它的平方数的末两位数也是___ab ，那么___ab 为__________. 5. 11某校初中二年级同学中，有45人参加了数学竞赛，有40人参加了英语竞赛，有38人参加了语文竞赛，其中参加数学和英语两科的共有15人，参加英语和语文两科的共有20人，参加数学和语文两科的共有19人.已知参加竞赛的同学中有114的同学得了奖，则得奖的共有______人. 6. 12用一个正方形去盖住边长为3，4，5的直角三角形，那么正方形的边长不得少于_______.7. 13计算9997959319753175311⨯⨯⨯+⋯⋯+⨯⨯⨯+⨯⨯⨯=_________. 8. 14万人瞩目的世博会在上海开幕了。

第十五届“五羊杯”初中数学竞赛
佚名
【期刊名称】《《中学数学研究》》
【年(卷),期】2004(000)003
【摘要】初一试题一、选择题(4选1型,每小题选对得5分,否则得0分.本大题满分50分.)1.2003和3002的最大公约数是( ).(A)1 (B)7 (C)11
(D)132.(16+1.63×2.87-125×0.115+0.0163×963)
【总页数】10页(P38-47)
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.2017年第二十九届“五羊杯”初中数学竞赛举办通告 [J], ;
2.2015年第二十七届“五羊杯”数学竞赛初中三年级试题 [J], ;
3.2015年第二十七届“五羊杯”数学竞赛初中一年级试题 [J], ;
4.2015年第二十七届“五羊杯”数学竞赛初中二年级试题 [J], ;
5.第二十五届“五羊杯”初中数学竞赛初二试题 [J],
因版权原因，仅展示原文概要，查看原文内容请购买。

初中数学初三竞赛测试测试考试题考点姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分一、计算题评卷人得分16．计算：．18．计算：17．（2015秋•莆田校级期末）计算：+2﹣1﹣2cos60°+（2﹣π）0．19．计算：．21．已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，B点坐标为（5,0）点C(0，5)，M为它的顶点.(1)求抛物线的解析式；(2)求△MAB的面积。

26．某住宅小区将现有一块三角形的绿化地改造为一块圆形的绿化地如图1．已知原来三角形绿化地中道路AB长为16米，在点B的拐弯处道路AB与BC所夹的∠B为45°，在点C的拐弯处道路AC与BC所夹的∠C 的正切值为2（即tan∠C=2），如图2．（1）求拐弯点B与C之间的距离；（2）在改造好的圆形（圆O）绿化地中，这个圆O过点A、C，并与原道路BC交于点D，如果点A是圆弧（优弧）道路DC的中点，求圆O的半径长．17．( 本小题满分10分)(1)计算：; (2)化简:19．已知多项式A=.求解：（1）化简多项式A；（2）若，求A的值.23．从1名男生和3名女生中随机抽取参加“我爱苏州”演讲比赛的同学．（1）若抽取1名，恰好是男生的概率为______________．11．如图，在坡度为1：3的山坡上种树，要求株距（相邻两树间的水平距离）是6米，则斜坡上相邻两树间的坡面距离是______________米（结果保留根号）．12．如图在平面直角坐标系中，二次函数的图象过正方形ABOC的三个顶点A、B、C，则值为__________。

18．如图，在平面直角坐标系xOy中，过点A(﹣2，0)的直线交y轴正半轴于点B，将直线AB绕着点O顺时针旋转90°后，分别与x轴、y轴交于点D、C,连接BD，若△ABD的面积是12，点B的运动路径长为_______.18．如图，M，N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞，工程人员为计算工程量，必须测量M、N两点之间的直线距离．选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM＝1千米，AN＝1.8千米，AB＝54米，BC＝45米，AC＝30米，求M、N两点之间的直线距离．24．如图1，抛物线与x轴交于A(1,0)，B(4，0)，与y轴交于点C.(1)求抛物线的解析式;(2)抛物线上一点D,满足，求点D的坐标;(3)如图2，已知N（0,1），将抛物线在点A、B之间部分（含点A、B）沿轴向上翻折，得到图象T（虚线部分），点M为图象T的顶点，现将图象T保持其顶点在直线MN上平移，得到的图象T1与线段BC至少有一个交点，求图象T1的顶点横坐标的取值范围.23．如图，一条公路的转弯处是一段圆弧（）．（1）用直尺和圆规作出所在圆的圆心；（要求保留作图痕迹，不写作法）（2）若的中点到弦的距离为m，m，求所在圆的半径.18．如图，在Rt△ABC中，∠BAC=90°，∠C=30°，以边上AC上一点O为圆心，OA为半径作⊙O，⊙O恰好经过边BC的中点D，并与边AC相交于另一点F．（1）求证：BD是⊙O的切线．（2）若AB=，E是半圆上一动点，连接AE，AD，DE．填空：①当的长度是______________时，四边形ABDE是菱形；②当的长度是______________时，△ADE是直角三角．6．已知⊙O的半径为r，圆心到点A的距离为d，且r，d分别是方程x2－4x＋3＝0的两根，则点A与⊙O 的位置关系是（）A．点A在⊙O内部B．点A在⊙O上C．点A在⊙O外部D．点A不在⊙O上2．下列二次函数中，其顶点坐标是（3，－2）的是（）A．B．C．D．3．如图汽车标志中不是中心对称图形的是（）A．B．C．D．1．的相反数是（）A．4B．-4C．D．7．如图，菱形ABCD的对角线AC，BD相交于点O，AC=8，BD=6，以AB为直径作一个半圆，则图中阴影部分的面积为（）A．25π-6B．π-6C．π-6D．π-62．已知|a|=5，=3，且ab＞0，则a+b的值为（）A．8B．﹣2C．8或﹣8D．2或﹣23．下列计算正确的是( )A．－＝0B．＋＝C．＝－2D．4÷＝23．一元二次方程的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．只有一个实数根D．没有实数根8．如图，⊙O的直径AB垂直于弦CD，垂足为E，∠A=22.5°，OC=4，CD的长为（）A．2B．4C．4D．81．下列图形中，中心对称图形有A．4个B．3个C．2个D．1个。

第十四届“五羊杯”初中数学竞赛试题解答吴康【期刊名称】《《中学数学研究》》【年(卷),期】2003(000)002【摘要】初一试题解答一、选择题:DABCACCABD1.(D).64×53=3392,643×5=3215,543×6=3258,63×54=340 2.显然其它的式子的计算结果都不能超过3402.2.(A).2002=2×7×11×13.易见它的不大于100的约数是1,2,7,11,13,2×7,2×11,2×13,7×11,7×13,共10个.3.(B).所求为1×3×7×9×11×13×17×19×…×91×93×97×99的个位数字,等于3^(10)×7^(10)×9^(10)的个位数字,等于21^(10)×81~5的个位数字,等于1.【总页数】7页(P33-39)【作者】吴康【作者单位】华南师范大学数学系510631【正文语种】中文【中图分类】G634.6【相关文献】1.第十三届"五羊杯"初中数学竞赛试题解答 [J], 吴康2.第十九届“五羊杯”初中数学竞赛试题解答 [J], 吴康;单墫;逄淑艳;曲政;游艳霞;陈海霞;曹琳;许鲔潮;石岩;张丽丽3.第十六届“五羊杯”初中数学竞赛试题解答 [J], 吴康;尤利华4.举办第十四届“五羊杯”初中数学竞赛通知 [J],5.第十四届“五羊杯”初中数学竞赛初二试题 [J],因版权原因，仅展示原文概要，查看原文内容请购买。