“教与学”优化算法研究综述

圆柱度误差及其评定方法综述
赵茜;王东霞;刘兰英
【期刊名称】《计量与测试技术》
【年(卷),期】2006(033)012
【摘要】针对圆柱度误差评定的特点,建立了四种圆柱度误差的数学模型,并将已有的圆柱度误差评定方法进行归纳分类,总结了各种方法的评定特点,同时阐述了圆柱度误差评定的最新研究成果即基于改进遗传算法的圆柱度误差评定,该成果可以推广应用到其它形状误差的评定.
【总页数】2页(P1-2)
【作者】赵茜;王东霞;刘兰英
【作者单位】南京工程学院自动化系,南京,211167;南京工程学院自动化系,南京,211167;南京工程学院自动化系,南京,211167
【正文语种】中文
【中图分类】TG8
【相关文献】
1.圆柱度误差包容评定为最小的投影图判断方法：线性鞍点规划方法的应用 [J], 安立邦;钱名海
2.基于遗传算法的机器零件圆柱度误差评定方法研究 [J], 陈强;张馨丹;孙连政;陶学恒
3.圆柱度误差快速最优化评定方法 [J], 薛小强;冯勇;贾炳辉
4.混合教与学算法的圆柱度误差评定方法研究 [J], 王生怀;王宸;徐风华
5.基于三坐标提取点数据的圆柱度误差的评定方法 [J], 温文炯;温英明
因版权原因，仅展示原文概要，查看原文内容请购买。

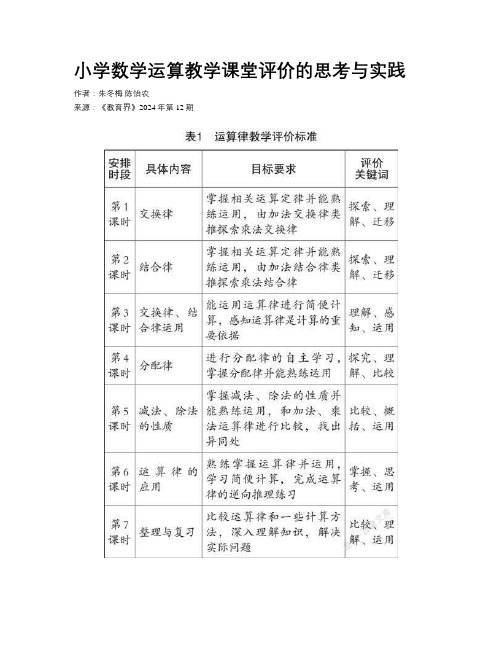
小学数学运算教学课堂评价的思考与实践作者：朱冬梅陈怡农来源：《教育界》2024年第12期【摘要】开展运算教学课堂评价的研究是学生运算能力培养策略研究的重要环节，也是落实“教学评一致性”的有效路径。

文章结合实践研究，阐述运算教学评价的价值和内涵逻辑，从教学实际出发阐述运算教学评价的进阶策略，以期有效突破评价的重难点，真正提高学生的运算学习效果，从而有效提升学生的核心素养。

【关键词】小学数学；运算教学；课堂评价运算能力是数学学习的基础，运算教学一直占据着小学数学教学的“半壁江山”。

运算教学评价具有重要的育人导向作用，是运算教学中的重要一环。

指向学生数学核心素养发展的运算教学课堂评价研究尤为重要，是实现知识教学向素养教学转变的重要路径，是实现学生学科核心素养发展的有效模式。

笔者从认识视角、教学逻辑、进阶策略三方面深入研究小学数学运算教学课堂评价。

一、梳理与整合：运算教学课堂评价的认识视角要想认识运算教学课堂评价，应充分考虑运算的本质内涵，有效结合运算教学的典型特征，具体实施教学评价，形成运算教学课堂评价的整体结构。

（一）小学数学运算教学应体现单元结构化特征小学数学运算教学应体现单元结构化的特征，将零散的知识点进行梳理、归纳和整合，构建整体结构和体系。

单元结构化视域下的运算教学，是基于学生对数学运算核心概念的需求，对教材内容、教学资源进行重新优化与重组，推动整体教学的教学方式［1］。

比如，对于运算律内容，苏教版教材是以运算形式为线索，先安排加法运算定律的内容，再安排乘法运算定律的内容，其他教材版本如北师大版是以运算律为线索，先安排交换律的内容，再依次安排结合律、分配律的内容。

在实际教学中，学生研究完加法交换律后，自然而然会产生疑问：加法有这样的运算定律，那乘法是不是也存在这样的运算规律？此时教师安排探究活动，学生容易通过迁移所学知识学习乘法交换律，这样的学习顺序更符合学生的学习规律。

由此，对于运算律这一内容，教师应以整体思维进行单元序列重组。

图像增强中优化算法适应度函数设计
施泽波
【期刊名称】《电光与控制》
【年(卷),期】2013(020)005
【摘要】确定图像非线性增强变换函数中最佳参数的通常做法是利用智能优化算法自动寻优,其中,优化算法中适应度函数的设计对于算法寻优的性能、图像增强的效果具有举足轻重的作用.目前,最常用的适用于图像质量评价的适应度函数仅是包含图像方差单一项,其实评价图像增强效果的重要因素还包括信息熵、紧致度、信噪改变量以及像素差别量等.据此,设计新的应用于图像非线性增强优化算法的适应度函数,充分考虑上述5种影响因素,并且兼顾图像的整体与局部,大的结构和小的细节平衡体现.将新设计的适应度函数用于遗传算法及粒子群算法对图像进行非线性变换增强实验,仿真结果表明,该算法具有较高的自适应性,且增强质量评价明显提高.【总页数】4页(P49-52)
【作者】施泽波
【作者单位】南京信息职业技术学院,南京210046
【正文语种】中文
【中图分类】V271.4;TP391
【相关文献】
1.基于改进的教与学优化算法的图像增强方法 [J], 毕晓君;潘铁文
2.GP在入侵检测规则提取中的适应度函数设计 [J], 王再见;傅忠谦;李斌;庄镇泉
3.一种采用改进蚁狮优化算法的图像增强方法 [J], 李宗妮;吴伟民;林志毅
4.模糊度函数法中适应度函数的自适应设计 [J], 宋高顺;王昌明;何云峰;陆建山
5.基于改进萤火虫优化算法的视频监控图像增强 [J], 俞文静; 刘航; 李梓瑞; 李基林因版权原因，仅展示原文概要，查看原文内容请购买。

一种应用于旅行商问题的莱维飞行转移规则蚁群优化算法
丁增良;陈珏;邱禧荷
【期刊名称】《计算机应用研究》
【年(卷),期】2024(41)5
【摘要】针对旅行商问题(TSP)提出了一种基于莱维飞行转移规则的蚁群优化算法。

该算法结合了基于莱维飞行和蚁群系统算法(ant colony system,ACS)的转移规则,形成了一种动态权重的混合转移规则,该策略能够有效地帮助算法跳出局部最优,增
强全局搜索能力。

此外,随机多路径优化3-opt策略通过随机抽取部分路径与当前
最优路径组合,增加算法的多样性。

当算法陷入停滞时,采用信息素平均随机重置策
略重置路径上的信息素浓度,有助于算法跳出局部最优。

实验结果显示,所提算法在
处理多个不同规模的TSP实例时,与最优解的误差保持在3%以内,证明了该算法在TSP中具备出色的收敛性和避免陷入局部最优解的能力。

【总页数】8页(P1420-1427)
【作者】丁增良;陈珏;邱禧荷
【作者单位】上海工程技术大学电子电气工程学院
【正文语种】中文
【中图分类】TP18
【相关文献】
1.基于莱维飞行的改进蚁群算法的PlD参数优化
2.基于莱维飞行的改进蚁群算法求解TSP问题
3.基于莱维飞行和布朗运动的鲸鱼优化算法
4.基于协同变异与莱维飞行策略的教与学优化算法及其应用
5.基于混沌映射和莱维飞行的黏菌优化算法
因版权原因，仅展示原文概要，查看原文内容请购买。

大数据视角分析进修变革——美国《通过教育数据开掘和进修分析增进教与学》报告解读及启示随着信息技术的迅猛进步，大数据已经成为引领各个领域进步的关键因素之一。

教育领域也不例外，大数据的应用正在逐渐改变教育的方式和效果。

近期，美国发布了一份名为《通过教育数据开掘和进修分析增进教与学》的报告，该报告从大数据的视角出发，对教与学的变革提出了一系列有益的启示。

该报告起首强调了教育数据开掘和进修分析的重要性。

传统上，教育的评估和决策主要依靠于有限的数据和个别的阅历。

而随着教育过程中各种在线进修平台和教育技术的兴起，大量的教育数据产生并存储了下来，为教与学的探究提供了珍贵的资源。

通过数据开掘和进修分析技术，我们能够发现隐藏在数据背后的规律和趋势，提供更详尽、更精准的评估和决策依据。

其次，该报告指出了教与学中存在的问题和挑战。

在传统的教学模式中，老师往往只能凭借有限的阅历和感觉来评估同砚的进修状况，并难以精确地猜测同砚的需要和潜力。

同时，同砚也面临着来自学业肩负、进修动力不足等问题，影响了进修的效果和效果。

这些问题需要通过大数据的分析和应用来解决。

在教育数据开掘方面，该报告提出了几个重要的探究方向。

起首是进修过程的模型建立和优化。

通过分析同砚的进修轨迹、进修风格等数据，可以建立同砚效果猜测模型，提供进修过程中的指导和支持。

其次是进修资源的个性化推举。

通过了解同砚的进修需求和爱好，可以为他们推举合适的进修资源，提高进修的效果和爱好。

最后是同砚行为的监测和预警。

通过对同砚的进修行为数据进行监测和分析，可以准时发现同砚的进修困难和问题，并提供相应的援助和支持。

在进修分析方面，该报告强调了同砚进修行为和结果的评估和反馈。

传统的考试和评估方式只能提供一个静态的结果，很难全面了解同砚的进修状况。

而通过进修分析，可以实时监测同砚的进修行为，并提供相应的反馈和建议。

同砚可以通过这些反馈来了解自己的进修状态和问题，准时调整进修策略和方法。

培养和激发学生的学习动机提高数学课堂教学的有效性摘要：学生具有强烈而自觉的学习动机，一般能专心听讲，认真完成作业，遇到困难时表现出极大的自制力和顽强的精神。

在课堂教学中，如何处理好教与学的关系，培养和激发学生的学习动机，提高课堂教学有效性，是当前教学改革中值得研究的重要课题之一。

关键词：激发动机情感探索有效学生进行学习总是为一定的学习动机所支配。

研究表明，学生具有强烈而自觉的学习动机，一般能专心听讲，认真完成作业，遇到困难时表现出极大的自制力和顽强的精神。

在课堂教学中，如何处理好教与学的关系，培养和激发学生的学习动机，提高课堂教学的有效性，是当前教学改革中值得研究的重要课题之一。

一、增强内部动机内部动机是一种指向学习任务的动机，求知的欲望。

教师在教学中，要利用一定的诱因使学生学习动机由潜伏状态转入活动状态，使之成为推动学习的内部动机,从而激发了学生的学习兴趣，并能不断促进学生思考、探索和创新。

1、“善待”错误，诱导学生的探究动机教学中由于学生受到知识经验、心理水平等因素制约，因此出错是在所难免的。

出现错误不完全是坏事，如果有效地加以利用，还会起到积极作用，化被动为主动，有利于加深新知的理解，引发学习兴趣。

当学生发生错误时，教师应该引导学生发现错误，自己主动探索，从中发现问题，而不是替代。

例如，教学利用商不变的规律进行除法简便计算时，教材上有这样一个例题：印刷厂包装8500本儿童读物，每200本装一包。

这些书可以装多少包，还剩多少本？学生计算时，利用“商不变的规律”把被除数和除数同时缩小100倍，即8500÷200=42（包）……1（本）。

教师明确告诉学生这个答案是错的，学生觉得奇怪怎么会错呢？这时有的学生用一般算法开始验算，结果得42余100；有的通过验算，结果不等于8500。

难道“商不变的规律”失效了吗？教师抓住时机引导学生展开讨论，从而得出：被除数和除数同时缩小100倍的时候，虽然商不变，但求出的余数也缩小了100倍，必须再把它扩大100倍。