基于反馈的精英教学优化算法
- 格式:pdf
- 大小:1.01 MB
- 文档页数:8

遗传算法在优化问题求解中的改进策略分析引言:遗传算法是一种基于自然选择和遗传机制而产生的优化算法。
它主要通过模拟生物进化过程中的遗传、交叉和变异等基本操作,来搜索问题的最优解。
然而,由于遗传算法在求解过程中存在一些局限性和不足,研究学者们提出了一些改进策略,以提高算法的收敛速度和求解精度。
本文将分析遗传算法在优化问题求解中的常见改进策略,并探讨其优点和不足。
一、精英保留策略精英保留策略是指在遗传算法的演化过程中保留上一代中的最优个体,不参与遗传操作,而直接复制到下一代中。
这种策略可以有效地防止优良基因的丢失,保持种群的多样性,并提高算法的收敛速度和求解精度。
通过精英保留策略,可以保证种群中至少有一个较优个体,从而减少了搜索空间的范围,加快了算法的收敛速度。
然而,精英保留策略也存在一些问题。
例如,当优秀个体较少时,精英保留策略可能导致种群陷入局部最优解而无法跳出。
此外,过多的精英保留也会增加算法的计算复杂度和存储空间。
二、种群多样性维持策略种群多样性维持策略是指通过一些手段来维持种群的多样性,避免早熟收敛和局部最优问题。
常见的策略包括杂交距离控制、变异概率控制、群体大小控制等。
杂交距离控制是通过设置杂交概率,限制执行杂交操作的个体之间的距离,防止过早收敛和进化陷入局部最优解。
变异概率控制是通过设定合适的变异概率,引入随机性来保持种群的多样性,并提高全局搜索能力。
群体大小控制是指根据优化问题的规模和复杂度来调整种群的大小,过小会导致缺乏多样性,过大则会浪费计算资源。
种群多样性维持策略的优点在于能够提高算法的全局搜索能力,避免算法过早陷入局部最优解。
然而,该策略也会增加计算复杂度和耗费存储空间。
三、自适应参数调节策略自适应参数调节策略是指根据算法的演化过程,动态调整算法中的参数,以提高算法的性能。
常见的自适应参数调节策略包括自适应变异概率、自适应杂交概率等。
自适应变异概率是根据种群的适应度情况动态调整变异概率的大小。

精英协同微粒群算法精英协同微粒群算法,也称为Elite Cooperative Particle Swarm Optimization (ECPSO)算法,是一种基于粒子群算法(Particle Swarm Optimization, PSO)的优化算法。
与传统的PSO算法不同,ECPSO算法引入了精英群体的概念,以提高算法的收敛速度和全局能力。
在粒子群算法中,每个个体表示一个解,称为粒子,而粒子的速度和位置则决定了其空间中的位置。
精英协同微粒群算法基于以下几个关键思想进行改进:1.精英群体:在ECPSO算法中,除了所有粒子外,还维护一个精英群体,包含当前找到的最优解。
精英群体的目的是引导其他粒子朝着更优的目标前进。
2.协同行为:每个粒子在更新自身速度和位置时,不仅要考虑自身的最优解和全局最优解,还要考虑精英群体的最优解。
这种协同行为使得粒子更加倾向于朝着全局最优解的方向移动。
3.多样性维持:为了避免算法陷入局部最优解,ECPSO算法引入了多样性维持的机制,通过随机化或者跳出局部最优解的策略,保持种群的多样性,从而更好地进行全局。
ECPSO算法的具体流程如下:1.初始化粒子的位置和速度,设置各种参数。
2.计算每个粒子的适应度,并记录当前最优解。
3.更新精英群体,如果一些粒子的适应度优于当前最优解,则将其设为新的全局最优解。
4.更新每个粒子的速度和位置,基于以下公式进行计算:V[i] = w * V[i] + c1 * rand( * (P[i] - X[i]) + c2 * rand( * (G - X[i])X[i]=X[i]+V[i]其中,V[i]表示粒子i的速度,X[i]表示粒子i的位置,w是惯性权重,P[i]是粒子i的最优解,G是全局最优解,c1和c2是加速系数,rand(是随机数生成函数。
5.判断终止条件,如果满足预设条件,则输出当前最优解,否则返回第3步。
ECPSO算法相比传统的PSO算法,在全局能力和收敛速度上有一定的提升。


教学评估与反馈计划建立有效的教学评估机制教师反馈三篇《篇一》教学评估与反馈计划对于建立有效的教学评估机制和教师反馈至关重要。
作为一名教育工作者,我深知教学评估的重要性,并希望能够通过建立一个详细的工作计划来提高教学质量和教师的专业发展。
从以下几个方面着手,以确保教学评估与反馈计划的有效实施:1.制定评估标准:明确教学评估的标准和指标,确保评估的客观性和公正性。
2.设计评估工具:根据评估标准,设计适合的评估工具,如问卷调查、课堂观察表等。
3.实施评估:对教师的教学进行评估,包括课堂表现、教学内容、学生反馈等方面。
4.反馈与改进:根据评估结果,向教师具体的反馈,并提出改进建议。
5.跟踪与监督:定期跟踪教师的改进情况,并必要的支持和指导。
6.第一阶段(1-2周):制定评估标准和指标,设计评估工具。
7.第二阶段(3-4周):对教师进行培训,介绍评估标准和工具的使用方法。
8.第三阶段(5-6周):开始对教师的教学进行评估,并收集学生反馈。
9.第四阶段(7-8周):向教师评估结果和反馈,并与教师讨论改进措施。
10.第五阶段(9-10周):教师根据反馈进行改进,并进行跟踪与监督。
工作的设想:通过建立有效的教学评估机制和教师反馈,我希望能够实现以下目标:1.提高教学质量:通过评估和反馈,帮助教师发现自身存在的问题,并采取相应的改进措施,从而提高教学质量。
2.促进教师专业发展:通过评估和反馈,激励教师不断学习和提升自己的教学能力,促进教师的专业发展。
3.提高学生满意度:通过评估和反馈,确保教学内容和方法能够满足学生的需求,提高学生的学习效果和满意度。
4.第一周:制定评估标准和指标,设计评估工具。
5.第二周:对教师进行培训,介绍评估标准和工具的使用方法。
6.第三周:开始对教师的教学进行评估,并收集学生反馈。
7.第四周:向教师评估结果和反馈,并与教师讨论改进措施。
8.第五周:教师根据反馈进行改进,并进行跟踪与监督。
9.确保评估标准的客观性和公正性,避免主观偏见的影响。

基于改进遗传算法的多目标优化算法研究随着计算机技术的不断发展,人们对于多目标优化算法的研究也越来越深入。
其中一种重要的算法就是遗传算法,它可以通过模拟遗传和自然选择的过程来寻找最优解。
然而,传统的遗传算法在处理多目标问题时存在一些限制,比如需要选择合适的权衡因子来平衡不同目标之间的关系,而这些选择往往具有主观性和难以确定性。
为了克服这些问题,人们提出了基于改进遗传算法的多目标优化算法,本文将对该算法进行深入探讨。
一、多目标优化问题的定义和分类多目标优化问题是指在同时优化多个相互独立或互相关联的目标函数时的优化问题。
其中,目标函数之间可能存在矛盾或冲突,需要进行权衡和平衡。
多目标优化问题可以分为线性和非线性问题,可分为确定性和随机性问题。
二、传统遗传算法的不足和改进传统遗传算法在多目标优化问题中存在的问题主要包括以下几个方面:(1)难以处理多样性问题由于传统遗传算法是基于群体的,因此不同个体之间容易出现相同的基因序列,从而导致种群过早收敛,难以保持种群的多样性。
(2)难以确定合适的权衡因子传统遗传算法在处理多目标问题时需要选择合适的权衡因子来平衡不同目标之间的关系,而这些选择往往具有主观性和难以确定性。
为了克服上述问题,人们提出了基于改进遗传算法的多目标优化算法。
其中,代表性的算法包括NSGA(Non-dominated Sorting Genetic Algorithm),SPEA(Strength Pareto Evolutionary Algorithm),MOEA/D(Multi-Objective Evolutionary Algorithm Based on Decomposition)等。
三、基于改进遗传算法的多目标优化算法1、NSGA算法NSGA算法是由Srinivas和Deb在1994年提出的,它通过构建非支配排序和拥挤度距离,实现了对多目标优化问题的有效处理。
它采用快速非支配排序方法(Fast Non-dominated Sorting)将所有个体分为多层次的档级,每个档级内都没有支配关系。
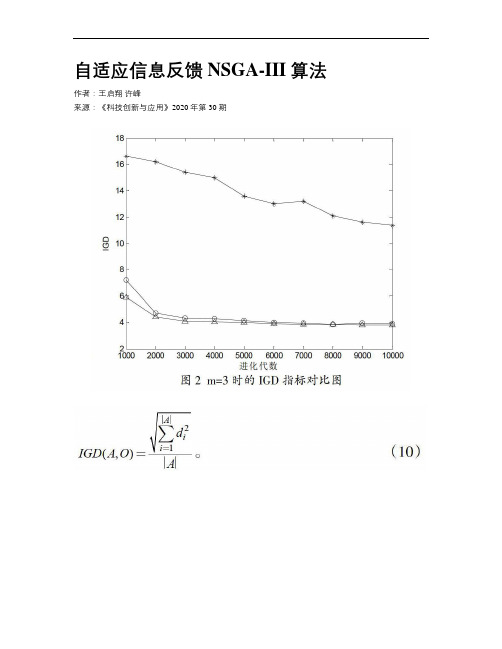
自适应信息反馈NSGA-III算法作者:王启翔许峰来源:《科技创新与应用》2020年第30期摘; 要:为了提高NSGA-III算法求解大规模高维多目标优化问题的能力,提出了一种基于自适应信息反馈机制的改进NSGA-III算法,其基本思想是:根据信息反馈原理,将当前代第k个个体与用NSGA-III算法求得的第i个个体加权平均后作为下一代第i个个体。
k的选取有指定和随机两种方式,可以根据目标函数的梯度自适应地选择。
采用大规模高维测试函数对新算法进行了性能测试,并与相关算法的结果进行了比较。
关键词:高维多目标优化;NSGA-III;信息反馈;自适应;目标函数梯度中图分类号:TP312 文献标志码:A 文章编号:2095-2945(2020)30-0020-04Abstract: In order to improve the ability of NSGA-III to solve large-scale many-objective optimization problems, an improved NSGA-III based on adaptive information feedback mechanismis proposed. Its basic idea is: according to the principle of information feedback, the weighted average of the kth individual in current generation and the ith individual obtained by NSGA-III is taken as the ith individual in next generation. There are two ways to select k: named and random,which can be adaptively selected according to the gradient of the objective function. The performance of new algorithm is tested by the large-scale many-objective test function, and the results are compared with those of related algorithms.Keywords: large-scale many-objective optimization; NSGA-III; information feedback; adaptive; objective function gradient通常,有两个或三个目标的优化问题称为多目标优化问题(Multi-objective Optimization Problems,MOP),而有四个或更多目标的问题称为高维多目标优化问题(Many-objective Optimization Problems,MaOP)。
nsga2算法通俗讲解摘要:1.NSGA2算法简介2.快速非支配排序3.拥挤度计算4.精英策略5.部分代码展示正文:SGA2(Non-Dominated Sorting Genetic Algorithm 2)是一种多目标优化算法,其在求解多目标优化问题时具有较高的性能。
NSGA2算法是基于遗传算法的,其主要创新点在于引入了非支配排序和拥挤度概念,以保持解的多样性和避免早熟现象。
1.NSGA2算法简介SGA2算法适用于复杂的多目标优化问题。
与单目标优化问题不同,多目标优化问题中各个目标之间存在相互制约关系,往往一个目标的优化会以其他目标的损失为代价。
NSGA2算法通过求解非劣解集(帕累托解集)来处理这种问题。
2.快速非支配排序在NSGA2算法中,快速非支配排序是核心部分。
该排序方法将解集合中的个体分为不同的等级,每个等级中的个体在所有目标函数上都具有优越性。
排序过程中,个体之间的支配关系通过比较目标函数值来判断。
例如,假设小明和小红分别是9岁50斤和8岁45斤,那么小明在岁数和体重上都优于小红,故小明支配小红。
3.拥挤度计算为了保持解的多样性,NSGA2算法引入了拥挤度概念。
拥挤度是指每个个体在解空间中的相对位置,可以通过计算个体在各个目标函数上的排名来获得。
在排序过程中,相同等级的个体之间比较拥挤度,以确定选择时的优先级。
4.精英策略SGA2算法采用精英策略来保存上一代的优秀个体。
在每一代中,除了通过交叉和变异产生的新个体外,还将上一代中的优秀个体直接遗传到下一代。
这样可以确保解集的多样性和收敛速度。
5.部分代码展示以下是一个简单的NSGA2算法实现部分代码展示:```pythonimport numpy as np# 定义目标函数def fitness_function(individual):return np.array([10 * individual[0] - individual[1], 2 * individual[0] + individual[1]])# 初始化种群population = np.random.rand(100, 2)# 快速非支配排序dominated_individuals = []ranking = np.zeros(100)for i in range(100):dominated = Falsefor j in range(i + 1, 100):if fitness_function(population[i]) <=fitness_function(population[j]):dominated = Truebreakranking[i] = 1 if dominated else 0# 计算拥挤度crowding_distance = np.zeros(100)for i in range(100):crowding_distance[i] = np.inffor j in range(i + 1, 100):if ranking[j] == ranking[i] andfitness_function(population[j]) <= fitness_function(population[i]):crowding_distance[i] = min(crowding_distance[i], fitness_function(population[j]) - fitness_function(population[i])) # 选择、交叉和变异selected_individuals = []for i in range(0, 50, 2):parent1 = population[np.argpartition(ranking, i)][0]parent2 = population[np.argpartition(ranking, i + 1)][0]child = np.array([parent1[0], parent2[1]])# 变异child[0] = np.random.randint(1, 10) if child[0] < 5 else 10 - child[0]selected_individuals.append(child)# 更新种群population = selected_individuals```通过以上代码,我们可以求解多目标优化问题并获得非劣解集。
教学中的反馈机制及时调整教学策略在教学过程中,反馈机制是非常重要的,它能够帮助教师及时了解学生的学习情况,并对教学策略进行调整。
本文将探讨教学中的反馈机制以及如何及时调整教学策略。
一、什么是教学中的反馈机制?教学中的反馈机制是指通过各种方式获取学生对教学内容的理解、学习情况以及掌握程度的信息,并以此为基础进行教学策略的调整。
反馈机制可以是直接的,如课堂上的讨论、问答和小组活动;也可以是间接的,如作业、测验和考试成绩。
二、为何需要反馈机制?1. 了解学生情况:通过反馈机制,教师能够了解学生对教学内容的理解程度和学术水平,从而能够有针对性地改进教学内容和教学方法。
2. 提供有效指导:教学中的反馈机制能够为学生提供及时的指导和反馈,使其认识到自己的不足之处,并采取相应的措施进行改进。
3. 调整教学策略:通过分析反馈信息,教师可以及时了解学生学习的困难和问题,并灵活调整教学策略,以更好地满足学生的需求。
三、如何有效使用反馈机制?1. 多样化的反馈方式:教师可以采用多样化的方式收集反馈信息,如课堂讨论、问答、小组活动等,以保证获得全面的学生反馈。
2. 及时回馈学生:教师应及时回馈学生的作业、测验和考试成绩,向学生解释其优点和不足之处,并提供改进建议,以激励学生进一步努力。
3. 学生自我反思:教师可以引导学生进行自我反思,通过对学习过程的分析和总结,帮助学生发现自己的问题和改进方向。
四、如何及时调整教学策略?1. 分析反馈信息:教师应仔细分析学生的反馈信息,了解他们的学习困难和问题,并找出可能存在的原因。
2. 个性化教学:根据学生的反馈信息,教师可以对教学内容进行个性化的调整,以满足不同学生的需求。
3. 引导学习:教师可以通过反馈信息调整教学策略,提供更加针对性的指导,引导学生主动参与学习,培养其自主学习的能力。
五、反馈机制中的挑战与解决方法1. 学生积极性不高:学生可能对反馈机制缺乏积极性,教师可以设置激励措施,如奖励机制,以增加学生的参与度。