结构力学位移法

位移法结构力学知识点概念讲解1.结构位移：结构在受力作用下会发生形变，而位移描述了结构各点之间的距离变化。

位移可以分为水平位移和竖向位移，用于表示结构在水平和竖直方向的变形情况。

2.自由度：结构的自由度是指结构中可以自由变动的独立变量的个数。

自由度越多，结构描述和计算的精度越高。

常见的自由度有平动自由度和转动自由度，平动自由度用于描述结构的水平位移，而转动自由度用于描述结构的转动变形。

3.约束条件：结构中存在的各种约束条件限制了结构的自由度。

约束条件是指结构中一些部分的位移受到限制，不能随意变动。

常见的约束条件有支座和铰链等，它们可以限制结构的平动和转动自由度。

4.单元：位移法将结构划分为若干个单元，每个单元由一组节点和单元内部的位移函数组成。

节点是指结构中的一些特定点，单元内部的位移函数用于描述该单元内部各处的位移情况。

6.节点位移：节点位移是指结构中各个节点的位移，它通过节点的约束条件和单元的位移函数之间的关系得到。

节点位移是位移法计算的核心内容，通过计算节点位移可以得到结构的变形和位移分布。

7.应变：结构在荷载作用下会发生应变，应变描述了结构内部各点的变形情况。

应变是位移的导数，可以通过位移的一阶导数来表示。

应变的计算是位移法中重要的步骤之一8.应力：结构在荷载作用下会发生应力，应力描述了结构各点的受力情况。

应力是力和单位面积的比值，可以通过应变和材料的本构关系得到。

应力的计算是位移法中重要的步骤之一通过以上的概念和知识点，位移法可以对不同类型的结构进行分析和计算。

它是结构力学中常用的方法之一，通过假设结构的位移函数和节点之间的位移关系，得到了结构的变形和位移的近似解。

在实际工程中，位移法广泛应用于桥梁、建筑物和各种结构的设计和分析中，具有重要的理论和实践意义。

结构力学中的位移法
位移法是基于以下假设的：结构单元之间的约束全部通过边界条件来
体现，结构中的材料是线弹性材料，结构中的每个单元之间是相互独立和
互不干扰的。

位移法的基本思想是首先假设结构的位移场，然后利用位移场的表达
式和边界条件，推导出结构的应力、应变和位移等信息。

具体步骤如下：
1.确定结构的约束条件：根据结构的平衡条件，确定结构各部分之间
的约束关系。

一般包括边界条件和连接条件等。

2.建立位移场：通过将结构的变形分解为一系列位移函数的线性组合，建立位移场。

常用的位移函数包括常数、线性函数、二次函数等。

3.推导位移场的表达式：利用结构的几何关系和材料的力学性质，根
据平衡条件和应力-应变关系，推导出位移场的表达式。

4.边界条件和连接条件：利用结构的边界条件和连接条件，确定位移
场中的待定系数。

5.应力和应变的计算：利用位移场的表达式和应力-应变关系，计算
结构中各点的应力和应变。

6.变形和位移的计算：利用位移场的表达式，计算结构中各点的变形
和位移。

7.校核：通过校核位移场的可行性和合理性，验证所得结果的准确性。

位移法的优点是可以处理各种复杂的边界条件和载荷情况，适用于各
种不规则结构。

但是位移法也存在一些局限性，如要求解一些复杂结构时，可能需要大量的计算和繁琐的推导过程。

总之，位移法是结构力学中一种重要的解决结构问题的方法，通过确定结构的位移场来分析结构的力学性能，具有广泛的应用前景。

在实际工程中，位移法被广泛运用于结构设计和分析中，是一种非常有效的结构分析方法。

力法和位移法的基本方程力法和位移法是结构力学中常用的两种分析方法。

力法是以外力为基础，通过计算结构内力来求解结构的变形和应力状态；位移法则是以结构变形为基础，通过计算结构位移来求解结构的内力和应力状态。

两种方法各有优缺点，应根据具体情况选择合适的方法进行分析。

力法的基本方程为平衡方程和应力-应变关系式。

平衡方程是指结构受到的外力与内力的平衡关系，可以用以下公式表示：∑F = 0其中，∑F表示结构受到的所有外力的合力，等于内力的合力。

这个方程可以用来计算结构的内力分布。

应力-应变关系式是指材料的应力与应变之间的关系，可以用以下公式表示：σ = Eε其中，σ表示应力，E表示弹性模量，ε表示应变。

这个方程可以用来计算结构的应力分布。

位移法的基本方程为位移-力关系式和应力-应变关系式。

位移-力关系式是指结构的位移与内力之间的关系，可以用以下公式表示：u = ∑(k_i)^(-1)F_i其中，u表示结构的位移，k_i表示第i个节点的刚度，F_i表示第i个节点的外力。

这个方程可以用来计算结构的内力分布。

应力-应变关系式同样适用于位移法，可以用来计算结构的应力分布。

需要注意的是，力法和位移法的基本方程只是分析结构的起点，具体的分析方法和计算过程还需要根据具体情况进行选择和确定。

同时，结构的材料性质、几何形状、边界条件等因素也会对分析结果产生影响，需要进行综合考虑。

总之，力法和位移法是结构力学中常用的两种分析方法，它们的基本方程为平衡方程和应力-应变关系式、位移-力关系式和应力-应变关系式。

在实际分析中，应根据具体情况选择合适的方法进行分析，并考虑结构的材料性质、几何形状、边界条件等因素。

第六章 位移法一、是非题1、位移法未知量的数目与结构的超静定次数有关。

2、位移法的基本结构可以是静定的，也可以是超静定的。

3、位移法典型方程的物理意义反映了原结构的位移协调条件。

4、结 构 按 位 移 法 计 算 时 ， 其 典 型 方 程的 数 目 与 结 点 位 移 数 目 相 等 。

5、位移法求解结构内力时如果P M 图为零，则自由项1P R 一定为零。

6、超 静 定 结 构 中 杆 端 弯 矩 只 取 决 于杆 端 位 移 。

7、位 移 法 可 解 超 静 定 结 构 ，也 可 解 静定 结 构 。

8、图示梁之 EI =常数，当两端发生图示角位移时引起梁中点C 之竖直位移为(/)38l θ（向下）。

/2/22l l θθC9、图示梁之EI =常数，固定端A 发生顺时针方向之角位移θ，由此引起铰支端B 之转角（以顺时针方向为正）是 -θ/2 。

θA B l 10、用位移法可求得图示梁B 端的竖向位移为ql EI 324/。

q l 11、图 示 超 静 定 结 构 ， ϕD 为 D 点 转 角 （顺 时 针 为 正）， 杆 长 均 为 l , i 为 常 数 。

此 结 构 可 写 出 位 移 法 方 程 111202i ql D ϕ+=/。

二、选择题1、位 移 法 中 ，将 铰 接 端 的 角 位 移 、滑 动支 承 端 的 线 位 移 作 为 基 本 未 知 量 ：A. 绝 对 不 可 ；B. 必 须 ；C. 可 以 ，但 不 必 ；D. 一 定 条 件 下 可 以 。

2、AB 杆 变 形 如 图 中 虚 线 所 示 ， 则 A 端的 杆 端 弯 矩 为 ：A.M i i i l AB A B AB =--426ϕϕ∆/ ;B.M i i i l AB A B AB =++426ϕϕ∆/ ;C.M i i i l AB A B AB =-+-426ϕϕ∆/ ;D.M i i i l AB A B AB =--+426ϕϕ∆/。

结构力学位移法基础结构力学是研究物体在外力作用下的形变规律的科学，力学位移法即利用力学方法来研究物体的位移情况。

在结构力学中，位移是一个重要的研究对象，通过分析物体的位移可以了解到物体在受力作用下的变形情况，进而判断物体的稳定性和结构的安全性。

结构力学中的位移分为线性位移和角位移两类，线性位移是指物体各个点在受力作用下发生的平移，角位移则是指物体各个点在受力作用下发生的旋转。

在分析物体的位移时，常常使用位移力法或位移力对单位位移法，这两种方法都是基于线性弹性假设，即假设物体在受到小变形作用后的恢复力是与变形量成正比的。

下面将详细介绍这两种方法。

位移力法是一种求解结构位移的经典方法，它通过建立刚度矩阵方程组来求解结构的位移分布。

首先，根据物体的几何形状和受力情况，将物体抽象为一个由节点和单元组成的有限元网格。

然后，在每个节点上建立位移和受力的关系方程。

根据平衡条件和边界条件，可以得到刚度矩阵和等效载荷矩阵，从而得到未知节点的位移。

位移力法适用于边界条件简单、结构体系简单的情况，但对于复杂的结构体系往往需要大量的计算量。

位移力对单位位移法是一种相对简化的位移计算方法，它通过按单位力对物体的位移进行分析，从而求解物体的刚度矩阵。

首先，施加单位力在物体上，并分析单位力产生的位移情况。

通过观察这些位移，可以得到物体刚度的一些性质。

然后，利用这些性质，可以建立未知位移与未知单位力之间的关系，从而得到未知节点的位移。

由于位移力对单位位移法不需要建立完整的刚度矩阵，因此适用于复杂的结构体系，具有计算量相对较小的特点。

结构力学位移法的基础是弹性力学理论，通过基本原理和假设推导出有限元法、弹性理论等方法，在工程实践中得到了广泛应用。

它不仅可以用于求解构件的位移情况，还可以用于求解应力和应变等力学参数。

在结构力学位移法研究中，常常需要使用计算机辅助手段，如有限元软件和编程语言等，来实现复杂结构体系的分析计算。

总之，结构力学位移法是研究物体位移规律的一种重要方法，通过分析物体的位移可以了解到物体的变形情况，从而评估其结构的安全性和稳定性。

第6章 位移法6.2等截面直杆的转角位移方程一、为什么要研究等截面直杆的转角位移方程1、位移法是以等截面直杆（单跨超静定梁）作为其计算基础的。

2、等截面直杆的杆端力与荷载、杆端位移之间恒具有一定的关系——“转角位移方程 ” 。

3、渐近法中也要用到转角位移方程。

二、杆端力的表示方法和正负号的规定1、弯矩：M AB 表示AB 杆A 端的弯矩。

对杆端而言，顺时针为正，逆时针为负；对结点而言，顺时针为负，逆时针为正。

2、剪力：Q AB 表示AB 杆A 端的剪力。

正负号规定同“材力”。

3、固端弯矩、固端剪力：单跨超静定梁仅由于荷载作用所产生的杆端弯矩称为固端弯矩，相应的剪力称为固端剪力。

用M AB 、M BA 、Q AB 、Q BA 表示。

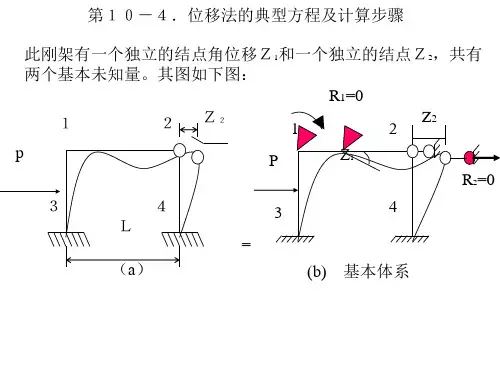
三、两端固定梁的转角位移方程1、线刚度2、弦转角四、一端为固定、另一端铰支的单跨超静定梁五、一端固定、另一端为滑动支座（定向支承）的单跨超静定梁B AM A B <0M B A >0Q A B >06.1 位移法的基本概念一、解题思路以图（b’）、（c’）（d’）分别代替图（b ）、（c ）、（d ）：二、解题示例φBz 1(a )(b )(c ) (d ) (b’) (c’)(d’)3ql/76.3 基本未知量数目的确定一、基本未知量1、结点角位移2、结点线位移二、基本假设1、小变形假设。

2、不考虑轴力和弯曲内力、弯曲变形之间相互影响。

（采用上述假设后，图示刚架有3个基本未知量。

）三、如何确定基本未知量1、在刚结点处加上刚臂。

2、在结点会发生线位移的方向上加上链杆。

3、附加刚臂与附加链杆数目的总和即为基本未知量数目。

四、确定线位移的方法（1）由两个已知不动点所引出的不共线的两杆交点也是不动点。

2M 1图MP 图M 图A（2）把刚架所有的刚结点（包括固定支座）都改为铰结点，如此体系是一个几何可变体系，则使它变为几何不变体系所需添加的链杆数目即等于原结构的独立线位移数目。

结构力学中位移法和力法的区别
结构力学是一门研究物体受力后形变和破坏情况的学科。

在结构力学中，常用的计算方法有位移法和力法。

这两种方法的区别主要体现在计算过程中所考虑的变量不同。

位移法主要是根据物体在受力后的位移情况来计算力的大小和
方向。

具体而言，首先通过等效应力原理将结构体分成若干个小单元，然后在每个小单元中计算出位移场和应力场，由此得到整个结构体的位移场和应力场，从而得到力的大小和方向。

力法则是根据物体受力后所受力的大小和方向来计算物体的变
形情况。

具体而言，首先在结构体中确定所有受力的部位和大小，然后根据受力部位和大小计算出结构体的内力和外力，最后根据内力和外力的平衡关系来求解结构体的变形情况。

总的来说，位移法更加适用于结构体变形较大的情况，而力法则更加适用于结构体变形较小的情况。

此外，两种方法的计算结果可能存在一定程度的误差，需要进行合理的校验和修正。

- 1 -。

第十七章位移法求解超静定结构的两种最基本的方法力法适用性广泛，解题灵活性较大。

（可选用各种各样的基本结构）。

位移法在解题上比较规范，具有通用性，因而计算机易于实现。

位移法可分为：手算——位移法电算——矩阵位移法力法位移法力法与位移法最基本的区别：基本未知量不同力法：以多余未知力基本未知量位移法：以某些结点位移基本未知量F PϕBϕB在忽略杆轴向变形和剪切变形的条件下，结点B 只发生角位移ϕB 。

由于结点B 是一刚结点，故汇交于结点B 的两杆的杆端在变形后将发生与结点相同的角位移。

位移法计算时就是以这样的结点角位移作为基本未知量的。

第一节位移法的基本概念BAClhEI 1EI 2首先，附加一个约束使结点B 不能转动，此时结构变为两个单跨超静定梁。

称为位移法的基本结构。

在荷载作用下，可用力法求得两根杆的弯矩图。

由于附加约束阻止结点B 的转动，故在附加约束上会产生一个约束力矩1631l F F P P -=C BAF P316Fl 532FlCAB然后，为了使变形符合原来的实际情况，必须转动附加约束以恢复ϕB 。

两个单跨超静梁在B 端有角位移时的弯矩图，同样可由力法求得。

此时在附加约束上产生约束力矩Bh EI lEI F ϕ⎪⎭⎫ ⎝⎛+=211143ϕB ϕBBA CB lEI ϕ13B h EI ϕ24B hEI ϕ22F PBAC求基本未知量,可分两步完成：1）在可动结点上附加约束，限制其位移，在荷载作用下，附加约束上产生附加约束力；2）转动附加约束使结点产生角位移ϕB ，使结构发生与原结构一致的结点位移。

ϕBϕB附加刚臂经过上述两个步骤，附加约束上产生约束力矩应为F 11和F 1P 之和。

由于结构无论是变形，还是受力都应与原结构保持一致，而原结构在B 处无附加约束，亦无约束力矩，故有F 11+F 1P ＝001634321=-⎪⎭⎫⎝⎛+Fl h EI lEI B ϕ解方程可得出ϕB 。

位移法典型方程将求出后ϕB ，代回图22-1c ，将所得的结果再与图22-1b 叠加，即得原结构（图22-1a ）的解。