2015江苏专转本英语

2022年真题：某高校3名学生响应国家号召，参军入伍。

在暂别校园、投身军营之际，学校决定为他们举行“强国有我，青春无悔”欢送仪式，请你以在校生代表的身份转写一份300字左右的发言稿。

2021年真题：××职业院校电影社团,定于2021年 3月29日下午 2∶00在校团委第一会议室举办“中国科幻电影20年”专题座谈会,届时××大学影视专业××老师将与同学们交流。

请以社团的名义,撰写一份300字左右的会议通知。

2020年真题.某高校团委拟举办“中华传统进校园”系列活动，现面向全校师生有奖征集本活动的形象标识(logo)。

请以该校团委的名义写一份征集启事。

要求: (1)字数300字左右。

(2) 内容充实，格式规范，语言得体。

(3)文中不得出现与考生本人有关的信息，如涉及校名、人名等，请用XX代替。

2019年真题.某报业集团面向高校毕业生招聘文字编辑，请根据职位要求，结合自身情况，写一封300字左右的求职信。

要求: (1)内容充实，格式规范，语言得体。

(2)文中不得出现与考生本人有关的信息，如涉及校名、人名等，请用xx代替。

2018年真题.为弘扬中华传统文化，某校文学院学生会拟牵头成立"古诗词创作学社”。

请你以文学院学生会的名义给校学生会写一份300字左右的申请书。

要求: (1)内容充实，文体规范，语言得体。

(3)文中不得出现与本人相关的信息，如涉及校名、人名等，请用XX代替。

2017年真题.某高校拟于 2017 年 5 月 4 日 19 点在校大礼堂举行“中华经典诗词吟诵”大赛，参加对象为大一学生。

请以该校团委的名义，拟写一份下发到各院（系）二级团组织的通知。

要求：（1）字数 300 字左右。

（2）内容充实，格式规范，语言得体。

（3）文中不得出现与考生本人有关的信息，如涉及校名、人名等，请用××代替。

2016年真题：某高校根据国家“志愿者服务计划”要求，在学生自愿申请、学校审核的基础上，选派5位同学去青海玉树地区支教半年，出发前拟举行“热血铸青春，青春西部行”欢送仪式。

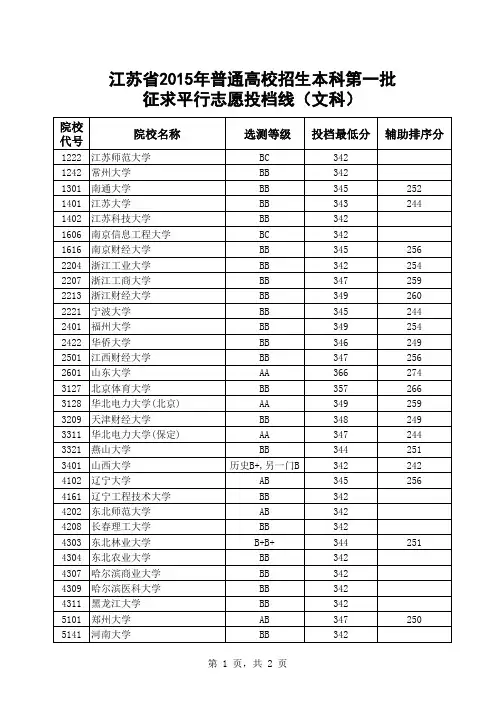
绝密★启用前江苏省2015年普通高校专转本选拔考试高等数学 试题卷注意事项：1．本试卷分为试题卷和答题卡两部分．试题卷共3页，全卷满分150分，考试时间120分钟． 2．必须在答题卡上作答，作答在试题卷上无效，作答前务必将自己的姓名和准考证号准确清晰地填写在试题卷和答题卡上的指定位置． 3．考试结束时，须将试题卷和答题卷一并交回．一、选择题（本大题共6小题，每小题4分，共24分，在下列每小题中，选出一个正确答案，请在答题卡上将所选的字母标号与黑） 1．当0=x 时，函数sin ()1e=−xf x 是函数()=g x x 的（ C ）．A ．高阶无穷小B ．低阶无穷小C ．同阶无穷小D ．等价无穷小解 sin 000()1e sin limlim lim 1()x x x x f x xg x x x→→→−−===−，答案：C ． 2．函数(1)=−x y x (1<x )的微分d y 为（ B ）．A ．(1)[ln(1)]d 1−−+−x xx x x xB ．(1)[ln(1)1−−−−x xx x x xC ．1(1)d −−x x x xD ．1(1)d −−−x x x x解 ln ln(1)y x x =−，1ln(1)1x y x yx ′=−−−，(1)[ln(1)]1x x y x x x ′=−−−−，d d (1)[ln(1)]d 1x xy y x x x x x′==−−−−，答案：B ． 3．0=x 是函数11e 10()e 110x xx f x x ⎧+⎪≠⎪=⎨−⎪⎪=⎩的（ B ）．A ．无穷间断点B ．跳跃间断点C ．可去间断点D ．连续点解 11e 1lim ()lim 1e 1xx x xf x −−→→+==−−，11110e 11e lim ()lim lim 1e 11exx x x x xxf x +−−−→→→−++===−−，答案：B ．4．设()F x 是函数()f x 的一个原函数，则(32)d −=⎰f x x ( A )．A ．1(32)2−−+F x cB ．1(32)2−+F x cC ．2(32)−−+F x cD ．2(32)−+F x c解11(32)d (32)d(32)(32)22f x x f x x F x c −=−−−=−−+⎰⎰，答案：A ． 5．下列级数条件收敛的是（ D ）．A ．()211n n nn∞=−−∑B ．11(1)21n n n n ∞=+−−∑C ．1!(1)∞=−∑nn n n n D ．211(1)∞=+−∑n n n n解 答案：D ． 6．二次积分()e11ln d ,d =⎰⎰yy f x y x （ D ）．A ．e11ln d (,)d ⎰⎰x x f x y yB ．1e0e d (,)d ⎰⎰x x f x y yC ．1e 00d (,)d ⎰⎰xx f x y yD ．1e 01d (,)d ⎰⎰x x f x y y解()e11e 1ln 01d ,d d (,)d xyy f x y x x f x y y =⎰⎰⎰⎰，答案：D ．二、填空题（本大题共6小题，每小题4分，共24分）7．设()lim(1)n n x f x n →∞=−，则(ln 2)=f ▲ ．12解 ()lim(1lim{[1()]}e n n x x x n n x x f x n n−−−→∞→∞=−=+−=，ln 21(ln 2)e 2f −==．8．设曲线33211⎧=−+⎪⎨=+⎪⎩x t t y t 在点(02)，处的切线方程为 ▲ ．32y x =+ 解 由2y =得1t =，22d d 3d d d 32d yy t t x x t t==−，1d 3d t y x ==，切线方程为23y x −=，即32y x =+． 9．设向量 b 与向量(121)=−− ，，a 平行，且12⋅=a b ，则= b ▲ ．(242)−−，，解 由于||a b ，所以(2)b a λλλλ==−− ，，，则4612a b λλλλ⋅=++== ，解得2λ=， 因而(242)b =−−，，．10．设1()21=+f x x ，则()()=n f x ▲ ．()1(1)2!()(21)n n n n n f x x +−⋅=+解 111()12122f x x x ==⋅++，()111(1)!(1)2!()12(21)()2n n n n n n n n f x x x ++−−⋅==++． 11．微分方程2′−=xy y x 满足初始条件12==x y 的特解为 ▲ ．2y x x =+ 解 由2′−=xy y x 得y y x x ′−=，于是有1()p x x=−，()q x x =，则有 11d d ()d ()de (()e d )e (e d )()xx p x xp x x x x y q x x c x x c x x c −−⎰⎰⎰⎰=+=+=+⎰⎰，又12==x y 得1c =，所以2y x x =+ 12．幂级数1)∞=−nn n x 的收敛域为 ▲ ．13[,22解2n n ==，则有1|1|2x −<，解得1322x <<，当12x =时，级数n n ∞=收敛，当32x =时，级数n ∞=发散，因而收敛域为13[,22 ． 三、计算题（本大题共8小题，每小题8分，共64分）13． 求极限020arcsin d lim2e 22→−−−⎰xxx t t tx x ．解 20200000arcsin d arcsin 2lim lim lim lim lim 12e 222e 222e 222e 2xxx x x x x x x x t t tx x x x xx x x x x→→→→→=====−−−−−−−−⎰．14． 设2sin 0()0−⎧≠⎪=⎨⎪=⎩x x x f x x x ，求()′f x ．解 当0x ≠时，243(1cos )(sin )22sin cos ()x x x x x x x x xf x x x −−−−−′==；当0x =时，232200001()(0)sin 1cos 12(0)lim lim lim lim 336x x x x xf x f x x x f x x x x →→→→−−−′=====． 所以32sin cos 0()106x x x xx x f x x −−⎧≠⎪⎪=⎨⎪=⎪⎩．15． 求通过直线112215x y z +−+==与平面32100++−=x y z 的交点．且与直线230240−++=⎧⎨+−−=⎩x y z x y z 平行的直线方程． 解 令112215x y z t +−+===，则有21x t =−，1y t =+，52z t =−，于是有 3(21)2(1)(52)100t t t −+++−−=，解得1t =，所以所求直线经过点(123)，，，依题意所求直线的方向向量11253211i j ks i j k =−=−++−，因而所求直线方程为123153x y z −−−==−．16．求不定积分3x ．解3x3sin x t=令3227sin 3cos d 27(1cos )sin d 3cos t t t t t t t =−⎰⎰2227(sin d cos sin d )27(cos cos d cos )t t t t t t t t =−=−+⎰⎰⎰ 39cos 27cos t t c=−+3sin xt =3122221(9)9(9)3x x c −−−+218)x c =++． 17． 计算定积分222()sin d ππ−+⎰x x x x ．解2222022222()sin d sin d sin d 2sin d x x x x x x x x x x x x x πππππππ−−−+=+=⎰⎰⎰⎰222202d cos 2(cos cos d )2sin 2x x x x x x xππππ=−=−−==⎰⎰．18． 设(())ϕ=，xz f x y ，其中函数f 具有二阶连续偏导数，函数ϕ具有连续导数，求2∂∂∂z x y ． 解 设x u y=，()v x ϕ=，则(,)z f u v =，121()z f x f x y ϕ∂′′′=+∂，2111212321()z x x x f f f x y y y y ϕ′∂′′′′′=−−−∂∂． 19． 计算二重积分d d ⎰⎰Dxy x y ，其中D为曲线=y =y x 及直线2=y 所围成的平面闭区域．解221d d d d 2yDxy x y y y x y x y ==⋅⎰⎰22421(2)d (14y y y y y =⋅−=−=．20． 已知2312e e e =++x x x y C C x 是二阶常系数非齐次线性微分方程()′′′++=y py qy f x 的通解，试求该微分方程．解 依题意对应齐次线性方程的特征方程为(1)(2)0r r −−=，即2320r r −+=，则对应齐次线性方程为320y y y ′′′−+=；设*3e x y x =，则*333e e 3(31)e x x x y x x ′=+⋅=+，*333e (31)e 3x x y x ′′=++⋅33(32)e x x =+，于是***3()32(23)e x f x y y y x ′′′=−+=+，则该微分方程为332(23)e x y y y x ′′′−+=+四、综合题（本大题共2小题，每小题10分，共20分）21．设D 是由曲线2=y x 与直线y ax =(0)>a 所围成的平面图形，已知D 分别绕两坐标轴旋转一周所形成的旋转体的体积相等，试求： （1）常数a 的值； （2）平面图形D 的面积．解 554012d 315a x a V a x x πππ=−=⎰，24401d 36a y a V y y a πππ=−=⎰． （1）依题意有x y V V =，解得54a =；（2）平面图形D 的面积223300111()d ()236aaS ax x x ax x a =−=−=⎰，当54a =时，315125(64384S ==． 22．设2()(1)+=+ax bf x x 在点1=x 处取得极值14−，试求： （1）常数，a b 的值；；（2）曲线()=y f x 的凹凸区间与拐点； （3）曲线()=y f x 的渐近线．解 243(1)()2(1)2()(1)(1)a x ax b x ax a bf x x x +−+⋅+−+−′==++．（1）依题意有11()44104a b b ⎧+=−⎪⎪⎨⎪−=⎪⎩ ，解得10a b =−⎧⎨=⎩；（2）31()(1)x f x x −′=+，3264(1)(1)3(1)42()(1)(1)x x x xf x x x +−−⋅+−′′==++，令()0f x ′′=，解得2x =．由表可知：曲线在(,2)−∞是凹的，在(2,)+∞是凸的，拐点为2(2,)9−；（3）由于2lim ()lim0(1)x x x f x x →∞→∞−==+，211lim ()lim (1)x x xf x x →−→−−==∞+，所以曲线有一条水平渐近线0y =，一条垂直渐近线1x =−．五、证明题（本大题共2小题，每小题9分，共18分） 23． 证明：当01<<x 时，(2)ln(1)2−−>x x x ． 证明 设()(2)ln(1)2f x x x x =−−−，2()ln(1)2ln(1)11x xf x x x x x−′=−−−=−+−−， 2211()01(1)(1)xf x x x x −′′=+=>−−−，因而当0x >时，()(0)0f x f ′′>=，从而有()(0)0f x f >=，即(2)ln(1)20x x x −−−>，即有(2)ln(1)2−−>x x x ．24． 设()=，z z x y 是由方程22()+=−y z xf y z 所确定的函数，其中f 为可导函数，证明∂∂+=∂∂z zxz y x y． 证明 依题意有2z z f xzf x x ∂∂′=−∂∂，1(22)z z x y z f y y∂∂′+=−∂∂ ，解得12z f x xzf ∂=′∂+，2112z xyf y xzf ′∂−=′∂+，于是有(21)2212121212z z xf z xyf xf xyzf z xf xyzf xf y xz y x y xzf xzf xzf xzf ′′′∂∂−+−+−++=+===′′′′∂∂++++．。

【导语】⽆忧考江苏专转本频道根据江苏省教育考试院发布的《》得知，2018年江苏专转本考试时间及科⽬安排具体如下：
1.考试时间
考试时间：2018年3⽉17⽇。

具体安排如下：
时间考试科⽬
9：00-11：00英语⽇语
13：00-15：00⾼等数学⼤学语⽂
16：00-17：30计算机基础
2.准考证发放
考前3天，考⽣可⾃⾏上打印《准考证》，或由推荐学校统⼀打印并发放考⽣《准考证》。

3.考点设置
省教育考试院根据报名⼈数及分布情况在相关院校设置考点，并尽量安排在标准化考点院校，考点院校具体负责考试的组织实施⼯作。

4.试卷保密保管
各市招考机构按教育考试有关要求，负责试卷的运送、保管等安全保密⼯作，指导所在辖区考点院校的考务管理与考务培训⼯作，并做好考试期间的巡视⼯作。

5.考试的组织实施，按照《江苏省2015年普通⾼校“专转本”选拔考试考务细则》（苏教考成〔2015〕2号）⽂件规定执⾏。

（三）⾃主招⽣的考试⼯作按省教育厅关于做好普通⾼校 “专转本”⾃主招⽣⼯作⽂件精神要求实施。

试点的6所⾃主招⽣接收院校，应认真组织命题与评卷（⾯试）⼯作，杜绝出现政治性、科学性和技术性错误。

要加强考试组织的规范化和试卷管理的安全保密，并做好考⽣的相关服务⼯作，确保⾃主招⽣试点⼯作安全、平稳、有序、顺利进⾏。

2015年湖北工程学院普通专升本考试计算机科学与技术专业招生人数、考试科目、复习教材和试题及录取分数线
招生院校：湖北工程学院招生人数：15（备注：该招生人数为教育厅下发通知时公布的招生计划，大部分学校最终会根据报考人数进行计划调整）
2015年湖北工程学院专升本计算机科学与技术专业考试科目
大学英语+高等数学+高级语言程序设计
2015年湖北工程学院专升本计算机科学与技术专业参考教材
1、大学英语：新世纪大学英语(综合教程2-3)上海外语教育出版社(2008年)秦秀白；
2、高等数学(上册)（本科少学时)(第三版)高等教育出版社（2006年）同济大学应用数学系；
3、高级语言程序设计：C程序设计（第四版）清华大学出版社（2010年）谭浩强
2015年湖北工程学院专升本计算机科学与技术专业录取分数线及要求
总分：122，英语：20
招生院校：湖北工程学院招生人数：15（备注：该招生人数为教育厅下发通知时公布的招生计划，大部分学校最终会根据报考人数进行计划调整）
2014年湖北工程学院专升本计算机科学与技术专业考试科目
大学英语+高等数学+高级语言程序设计
2014年湖北工程学院专升本计算机科学与技术专业参考教材
新世纪大学英语(综合教程3)，上海外语教育出版社(2008年),秦秀白。

高等数学(上册)，(本科少学时)(第三版)，高等教育出版社（2006年），同济大学应用数学系。

C程序设计（第四版），清华大学出版社（2010年），谭浩强。

2014年湖北工程学院专升本计算机科学与技术专业录取分数线及要求
计算机科学与技术录取分数线: 总分>=122,英语>=20，按总分从高到低录取。

2018年江苏五年一贯制专转本（五年制专转本）英语复习技巧2018江苏专转本还有两个月就开始考试了，江苏南京、无锡，常州、苏州、徐州、南通、淮安、扬州、盐城、连云港，泰州、镇江、宿迁五年制专转本自学通过率高吗？需要报辅导班吗？五年制专转本是五年制高职在校生通过全省统一的考试，考取后能到主考院校学习两年，毕业后拿到的是全日制本科文凭。

江苏省无锡市、常州市、南京市、苏州市、连云港、泰州、镇江、徐州、张家港、昆山五年制专转本考试科目是英语+两门专业课。

选拔方式为统一考试择优录取，分数从高到低。

五年制专转本通过率也是按照每年的报考总人数，所以近三年报考人数增加很多，以前总有家长认为高中都考不上，还上什么本科。

从2017年开始，大多数的家长和学生意识已经转变很快。

都了解五年制专转本是全日制本科学历，争先恐后给孩子报各式各样的辅导班或者网上购买所谓的考试资料。

做任何事情家长和学生需要方法，方法对了，事倍功半！以下是小编总结的转本英语心得，希望对专转本的同学有帮助1.转本英语的语法和大纲要求在4级以下。

小编的经验你要多复习词汇，主要攻克词汇中介词的运用和各种不同介词但是动词一样的搭配，搞清楚到底是什么意思，因为真的常考，例如：break down和break out就是这样的单词必须一一搞懂；2.选择的第2个难点在于长短句的分析，定语从句、状语从句的主句分局分析一定要透彻3.倒装是一个很重要的考点，建议你在语法上，一定要搞清楚什么单词出现用倒装以上三点虽然只有3点，但是知识面广，需要积累，你赶紧抓紧时间把。

很多家长都知道五年制专转本考英语，那么就在外面到处报英语班.。

其实大多数家长都犯了误区，英语分好多种，有公共英语，大学英语四六八，雅思、托福、牛津都有，那么五年制专转本英语考试是专转本英语。

考试的侧重点都不一样，而且拉分极高。

所以到博大专转本培训，老师会根据针对性较强的考试内容辅导。

专业课，有的学生基本的没上过，自己在家看书，如何检测自己的学习成果？连考试题型都不知道。