萤火虫算法-matlab代码

BLDC电机的分数阶PID转矩控制：MFA-PSO方法的应用摘要：为了进一步优化FOPID控制器的性能，将改进的萤火虫算法(MFA)与粒子群优化(PSO)相结合，对FOPID的参数进行了优化。

在Matlab/Simulink环境中，对这一基于MFA-PSO的FOPID控制策略进行了仿真研究。

为了评估该控制器在无刷直流电机控制中的适用性，我们还将其与通过遗传算法(GA)、萤火虫算法(FA)以及基于萤火虫人工神经网络(ANN)的FOPID控制器进行了结果对比。

关键词：BLDC电机；电机转矩控制；PID控制引言典型的PID控制器由于其简单性和较好的稳态性能，被广泛应用于无刷直流电机(BLDCM)的控制。

但是，当负载发生变化时，PID控制器存在不确定性的问题。

此外PID控制器的整定也会增加结构参数的不确定性。

为克服上述问题，提出了一种基于FOPID控制器的策略，此控制器可以为BLDCM提供精确的控制方法。

一、研究背景与研究意义无刷直流电机（BLDC电机）已广泛应用于各种领域，包括家用电器、工业设备、电动汽车、航空航天等。

与传统的有刷电机相比，BLDC电机具有更高的效率、更长的使用寿命和更小的维护需求，这是因为它们消除了物理碳刷的需要，从而减少了摩擦和磨损。

由于其这些显著优点，BLDC电机已成为众多应用中的首选电机解决方案。

传统的PID控制器由于其简单性和稳态性能而被广泛使用，特别是在初级控制系统中。

然而，传统PID控制器也存在一些明显的局限性。

[1]另外PID控制器的参数调整可能是一个困难和耗时的过程，尤其是在复杂或非线性的系统中。

为了解决这些挑战，研究人员开始考虑更先进、灵活和健壮的控制策略，其中之一就是分数阶PID（FOPID）控制器。

与传统PID控制器相比，FOPID控制器引入了额外的自由度，使其在面对系统动态变化和不确定性时具有更好的控制性能。

[2]其核心思想是在PID控制的基础上增加了分数阶导数和积分，这样不仅可以更精确地匹配系统的动态行为，而且还可以改善系统的鲁棒性。

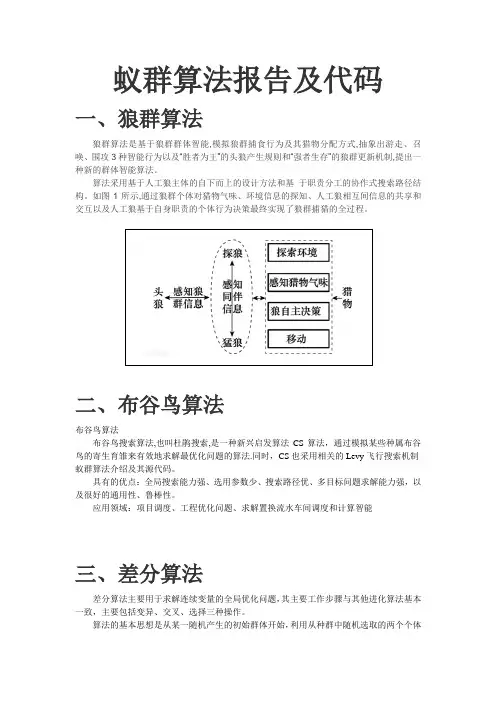
蚁群算法报告及代码一、狼群算法狼群算法是基于狼群群体智能,模拟狼群捕食行为及其猎物分配方式,抽象出游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出一种新的群体智能算法。

算法采用基于人工狼主体的自下而上的设计方法和基于职责分工的协作式搜索路径结构。

如图1所示,通过狼群个体对猎物气味、环境信息的探知、人工狼相互间信息的共享和交互以及人工狼基于自身职责的个体行为决策最终实现了狼群捕猎的全过程。

二、布谷鸟算法布谷鸟算法布谷鸟搜索算法,也叫杜鹃搜索,是一种新兴启发算法CS算法，通过模拟某些种属布谷鸟的寄生育雏来有效地求解最优化问题的算法.同时，CS也采用相关的Levy飞行搜索机制蚁群算法介绍及其源代码。

具有的优点：全局搜索能力强、选用参数少、搜索路径优、多目标问题求解能力强，以及很好的通用性、鲁棒性。

应用领域：项目调度、工程优化问题、求解置换流水车间调度和计算智能三、差分算法差分算法主要用于求解连续变量的全局优化问题，其主要工作步骤与其他进化算法基本一致，主要包括变异、交叉、选择三种操作。

算法的基本思想是从某一随机产生的初始群体开始，利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源，将差向量加权后按照一定的规则与第三个个体求和而产生变异个体，该操作称为变异。

然后，变异个体与某个预先决定的目标个体进行参数混合，生成试验个体，这一过程称之为交叉。

如果试验个体的适应度值优于目标个体的适应度值，则在下一代中试验个体取代目标个体，否则目标个体仍保存下来，该操作称为选择。

在每一代的进化过程中，每一个体矢量作为目标个体一次，算法通过不断地迭代计算，保留优良个体，淘汰劣质个体，引导搜索过程向全局最优解逼近。

四、免疫算法免疫算法是一种具有生成+检测的迭代过程的搜索算法。

从理论上分析，迭代过程中，在保留上一代最佳个体的前提下，遗传算法是全局收敛的。

五、人工蜂群算法人工蜂群算法是模仿蜜蜂行为提出的一种优化方法，是集群智能思想的一个具体应用，它的主要特点是不需要了解问题的特殊信息，只需要对问题进行优劣的比较，通过各人工蜂个体的局部寻优行为，最终在群体中使全局最优值突现出来，有着较快的收敛速度。

摘要萤火虫算法(Firefly Algorithm,FA)是受自然界中的萤火虫通过荧光进行信息交流这种群体行为的启发演变而来。

它是由剑桥大学的Xin-She Yang教授在2009年提出的，它作为一种新颖的仿生群智能优化算法，有较大的研究空间。

近几十年来随着越来越多的仿生群智能算法的提出，人们对于这些算法的认识和研究也逐步加深。

本文先介绍群智能优化算法的理论概念，然后着重通过对萤火虫算法仿生原理的了解，从数学的角度对萤火虫算法进行合理的描述和过程的定义，最后编写该算法的matlab代码实现对3个峰值函数进行仿真测试，得出其测试结果。

同时用遗传算法对同样的测试函数也进行仿真测试，得出其测试结果。

最后通过测试结果比较萤火虫算法和遗传算法分别在对峰值函数寻优结果的精确度。

在比较过程中，可以根据测试结果发现，萤火虫算法在对峰值函数的寻优结果的精确度优于遗传算法。

这表明了萤火虫算法在连续空间优化的可行性和有效性，同时也表明了萤火虫算法具有良好的应用前景。

关键词：萤火虫算法，仿生群智能优化算法，优化分析，遗传算法ABSTRACTThe Firefly Algorithm (FA) is affected by the nature of the Firefly exchange of information through a fluorescence inspired this kind of crowd behavior has evolved. It is made by Xin - She Yang professor at the university of Cambridge in 2009, as a novel bionic swarm intelligent optimization algorithm, has a large research space. In recent decades as more bionic swarm intelligent algorithm is put forward, people also gradually deepen to the understanding and research of those algorithms.First，it is introduced in this paper theoretical concepts of swarm intelligence optimization algorithm, and then emphatically through the understanding of firefly algorithm bionic principle, from the perspective of mathematical descriptions of firefly algorithm is reasonable and the definition of the process, finally ,writes matlab code of the algorithm to realize the three peak function simulation test, to test results. At the same time with the genetic algorithm on the same test function, simulation test, to test results. Finally by comparing test results of firefly algorithm and genetic algorithm in the accuracy of the optimization results of peak function respectively. In the process of comparison, according to the result of test, it can shows that the firefly algorithm on the accuracy of the optimization results of peak function is superior to genetic algorithm. It shows that the feasibility and effectiveness of firefly algorithm in the continuous space optimization, but also shows that the firefly algorithm has a good application prospect.Keywords:firefly algorithm, The bionic swarm intelligent optimization algorithm, Optimization analysis, genetic algorithm目录摘要 (I)ABSTRACT (II)目录 ...................................................................................................................................... I II 第一章绪论 . (1)一、研究的背景及意义 (1)二、群智能优化算法的研究现状 (1)三、本论文的内容和结构 (2)第二章群智能优化理论 (4)一、群智能优化算法的概述 (4)二、模拟退火算法 (4)三、遗传算法 (5)四、蚁群算法 (7)五、粒子群优化算法 (8)六、人工萤火虫群优化算法 (9)七、人工鱼群算法 (11)第三章萤火虫算法 (13)一、萤火虫算法的概念 (13)二、萤火虫算法的国内外研究现状 (13)三、萤火虫算法的仿生原理 (14)四、萤火虫算法的数学描述与分析 (15)五、萤火虫算法的流程 (16)六、实现萤火虫算法的matlab代码 (16)第四章仿真实验与分析 (22)一、三个测试函数的介绍 (22)二、FA和GA对F1(x)的仿真测试 (22)三、FA和GA对F2(x)的仿真测试 (25)四、FA和GA对F3(x)的仿真测试 (27)五、测试结果分析 (30)结论 (31)致谢 (32)参考文献 (33)第一章绪论一、研究的背景及意义在现实生活中，许多优化问题要求人们不仅要计算出其极值，还要得出其最优值。

一种新颖的改进萤火虫算法
左仲亮;郭星;李炜
【期刊名称】《微电子学与计算机》
【年(卷),期】2017(34)9
【摘要】为了克服原始萤火虫算法(Glowworm swarm optimization,GSO)对于多峰函数寻优精度不高和后期收敛速度较慢的问题.为此,本文针对性的提出了一种改进的动态步长自适应的萤火虫优化算法.采用该算法的改进思想,能在一定的程度上避免算法因为过早的成熟而陷入局部最优,并且改进的算法比原始萤火虫算法有着更好的收敛精度.Matlab实验仿真表明,改进算法在一定程度上提高了收敛速度和寻优精度.
【总页数】5页(P15-19)
【关键词】萤火虫算法;多峰函数;动态步长;自适应
【作者】左仲亮;郭星;李炜
【作者单位】安徽大学计算智能与信号处理重点实验室;安徽大学计算机科学与技术学院
【正文语种】中文
【中图分类】TP393
【相关文献】
1.一种新颖的仿生群智能优化算法:萤火虫算法 [J], 刘长平;叶春明
2.一种改进的模拟退火萤火虫混合算法求解0/1背包问题 [J], 任静敏; 潘大志
3.一种基于深度学习的改进萤火虫频谱分配算法 [J], 苏慧慧; 彭艺; 曲文博
4.一种基于深度学习的改进萤火虫频谱分配算法 [J], 苏慧慧; 彭艺; 曲文博
5.一种新颖的萤火虫算法求解PID控制器参数自整定问题 [J], 顾忠伟;徐福缘因版权原因，仅展示原文概要，查看原文内容请购买。

function fa_ndimpara=[20 500 0.5 0.2 1];help fa_dim.m% 定义问题维度d=15;Lb=zeros(1,d);Ub=2*ones(1,d);u0=Lb+(Ub-Lb).*rand(1,d);[u,fval,NumEval]=ffa_mincon(@cost,u0,Lb,Ub,para);%Display resultsbestsolution=u;bestojb=fval;total_number_of_function_eveluation=NumEval;%目标函数function z=cost(x)%准确的结果应该是（1,1,1...1）z=sum((x-1).^2);%开始执行萤火虫算法function[nbest,fbest,NumEval]=ffa_mincon(fhandle,u0,Lb,Ub,para) if nargin<5,para=[20 500 0.25 0.20 1];endif nargin<4,Ub=[];endif nargin<3,Lb=[];endif nargin<2,disp('Usuage:FA_mincon(@cost,u0,Lb,Ub,para)');endn=para(1);MaxGeneration=para(2);alpha=para(3);betamin=para(4);gamma=para(5);%函数运算次数NumEval=n*MaxGeneration;%检查是否越过上限if length(Lb)~=length(Ub);disp('Simple bounds/limits are improper! ');returnend%计算维度d=length(u0);%初始化向量zn=ones(n,1)*10^100;%生成萤火虫位置[ns,Lightn]=init_ffa(n,d,Lb,Ub,u0);for k=1:MaxGeneration, %开始迭代alpha=alpha_new(alpha,MaxGeneration);%评估新解for i=1:n,zn(i)=fhandle(ns(i,:));Lightn(i)=zn(i);end%根据亮度强弱排列萤火虫[Lightn,Index]=sort(zn);ns_tmp=ns;for i=1:n,ns(i,:)=ns_tmp(Index(i),:);end%找到当前最优nso=ns;Lighto=Lightn;nbest=ns(1,:);Lightbest=Lightn(1);fbest=Lightbest;%所有的萤火虫飞向最亮的萤火虫[ns]=ffa_move(n,d,ns,Lightn,nso,Lighto,nbest,Lightbest,alpha,betamin,ga mma,Lb,Ub);end%迭代结束%*******子函数***************%萤火虫位置初始化function[ns,Lightn]=init_ffa(n,d,Lb,Ub,u0)if length(Lb)>0,for i=1:n,ns(i,:)=Lb+(Ub-Lb).*rand(1,d);endelsefor i=1:n,ns(i,:)=u0+randn(1,d);endend%初始化亮度Lightn=ones(n,1)*10^100;%所有的萤火虫飞向最亮的萤火虫function[ns]=ffa_move(n,d,ns,Lightn,nso,Lighto,nbest,Lightbest,alpha,be tamin,gamma,Lb,Ub)scale=abs(Ub-Lb);for i=1:n,for j=1:n,r=sqrt(sum((ns(i,:)-ns(j,:)).^2));if Lightn(i)>Lighto(j), %Brighter and more attractivebeta0=1;beta=(beta0-betamin)*exp(- gamma*r.^2)+betamin;tmpf=alpha.*(rand(1,d)-0.5).*scale;ns(i,:)=ns(i,:).*(1-beta)+nso(j,:).*beta+tmpf;endendend%检查更新的解是否在限制范围内[ns]=findlimits(n,ns,Lb,Ub);% This function is optional,as it is not in the original FA% The idea to reduce randomness is to increase the convergence,% however,if you reduce randomness too quickly,then premature% convergence can occr.So use with care.function alpha=alpha_new(alpha,NGen)delta=1-(10^(-4)/0.9)^(1/NGen); alpha=(1-delta)*alpha;%确保萤火虫在限制范围内移动function[ns]=findlimits(n,ns,Lb,Ub) for i=1:n,%下限ns_tmp=ns(i,:);I=ns_tmp<Lb;ns_tmp(I)=Lb(I);%上限J=ns_tmp>Ub;ns_tmp(J)=Ub(J);%更新运动ns(i,:)=ns_tmp;end。

基于动态自适应萤火虫优化算法郗君甫【摘要】为了有效解决标准萤火虫算法在寻优过程中存在易陷入后期收敛速度较慢、寻优精度不高等问题,在位置更新公式中引入动态调整惯性权重和自适应步长机制,提出一种动态自适应萤火虫优化算法.利用四个标准测试函数进行仿真实验结果表明,动态自适应萤火虫算法具有更快收敛速度、较高求解精度和稳定性.【期刊名称】《邢台职业技术学院学报》【年(卷),期】2017(034)005【总页数】5页(P78-82)【关键词】萤火虫优化算法;惯性权重;自适应【作者】郗君甫【作者单位】邢台职业技术学院信息工程系,河北邢台 054035【正文语种】中文【中图分类】TP181萤火虫优化（Glowworm Swarm Optimization, GSO）算法是印度学者K.N.Krishnanand和D.Ghose于2005年提出的一种新型的仿生群智能优化算法[1,2]，其算法基本思想是单体萤火虫在搜索区域内利用发光亮度不同的特性寻找并聚合同伴，亮度越高吸引同伴能力越强，通过不断移动位置，实现寻优。

该算法由于模型简单、稳定性强、寻优能力强等优点，目前成为智能计算领域一个新的研究热点，随着研究不断深入已广泛应用于优化问题[3]、预测问题[4,5]、电力系统[6]、路径规划[7]、自动控制[8]、图像处理[9]、组合问题[10,11]等多个领域，并取得较好效果，但GSO算法也存在容易陷入局部最优、早熟收敛、后期收敛较慢和求解精度不高等问题。

针对基本萤火虫优化算法的缺陷，通过研究理论分析后，提出一种动态自适应萤火虫优化（Dynamic adaptive Glowworm Swarm optimization，DAGSO）算法，在算法中引入动态调整惯性权重机制和自适应步长机制，更好协调好局部搜索和全局搜索之间的关系，通过仿真实验结果表明，DAGSO算法有效改善了全局和局部搜索能力、提高收敛速度和寻优精度。

在标准GSO算法中，萤火虫群中单体萤火虫随机分布在解空间中，每个单体萤火虫均拥有荧光素和感知半径，单体萤火虫的荧光素亮度与所在位置上目标函数有关，单体萤火虫越亮，表明荧光素值越大、位置越好、目标函数值越优。

萤火虫算法萤火虫算法是一种著名的算法，由美国数学家和数学大师帕森斯在1965年提出。

该算法是一个线性规划问题，其方法是先进行一个初始条件的求解，并将原始的求解结果，以“最小化函数”等形式保留下来。

此算法可用于各种数学计算领域，如：智能电网、自动驾驶等。

在传统优化问题中，人们一般采用的多项式权重方法存在计算时间长、结果不稳定、计算量大、不可预测等问题。

而萤火虫计算方法不但能够求得最优解，还能将每个变量之间的交互作用尽量控制在最小范围内。

1、先进行一个初始条件的求解，并将原始的求解结果以“最小化函数”等形式保留下来。

其中, x i (i=1)=0表示在初始条件下, i=1求最优解的平均路径长度, i=1求最优解的平均路径长度。

对于不同的种群，这种方法存在一定的差异：当一个种群没有达到某个状态时，其求解方法是先使用对这个种群影响最大的状态值(x i=1)来求解这一状态；如果种群的所有个体都处于这一状态时，则求解其最终状态为: x i=1求最优解的平均路径长度。

具体方法如下：其中b i=1为该种群的最小路径长度; c i=1表示该种群是一种具有适应能力的种群; d i=1表示种群适应能力相对较弱; e j (i为种群个体数）表示为当前种群的最小迭代次数; j为全局优化变量之间相互关联的权重因子; x i (i为种群状态值）表示该基因表达能力的全局相关系数或局部相关系数(x i— n)=1/2; z s为个体数。

2、然后通过随机抽取某些变量并将结果计算出一个可行值，该值与变量之间的交互作用最小，因此选取权重得到最优解；萤火虫算法是一种基于“数理”的优化方法，它在求解线性规划问题中有着广泛应用。

然而也正因为如此，有很多学者将该算法归为一类机器学习问题进行深入研究。

由于萤火虫算法是一种基于“数理”的优化方法，因此也有了许多其他学者将它归入机器学习、计算机科学、信息科学等领域。

但总体上来说，萤火虫算法仍然属于机器学习的范畴，而这与其复杂程度与广泛应用有着很大的关系。

第八章萤火虫算法8.1介绍萤火虫（firefly）种类繁多，主要分布在热带地区。

大多数萤火虫在短时间内产生有节奏的闪光。

这种闪光是由于生物发光的一种化学反应，萤火虫的闪光模式因种类而异。

萤火虫算法(FA)是基于萤火虫的闪光行为，它是一种用于全局优化问题的智能随机算法，由Yang Xin-She（2009）[1]提出。

萤火虫通过下腹的一种化学反应-生物发光（bioluminescence）发光。

这种生物发光是萤火虫求偶仪式的重要组成部分，也是雄性萤火虫和雌性萤火虫交流的主要媒介，发出光也可用来引诱配偶或猎物，同时这种闪光也有助于保护萤火虫的领地，并警告捕食者远离栖息地。

在FA中，认为所有的萤火虫都是雌雄同体的，无论性别如何，它们都互相吸引。

该算法的建立基于两个关键的概念：发出的光的强度和两个萤火虫之间产生的吸引力的程度。

8.2天然萤火虫的行为天然萤火虫在寻找猎物、吸引配偶和保护领地时表现出惊人的闪光行为，萤火虫大多生活在热带环境中。

一般来说，它们产生冷光，如绿色、黄色或淡红色。

萤火虫的吸引力取决于它的光照强度，对于任何一对萤火虫来说，较亮的萤火虫会吸引另一只萤火虫。

所以，亮度较低的个体移向较亮的个体，同时光的亮度随着距离的增加而降低。

萤火虫的闪光模式可能因物种而异，在一些萤火虫物种中，雌性会利用这种现象猎食其他物种；有些萤火虫在一大群萤火虫中表现出同步闪光的行为来吸引猎物，雌萤火虫从静止的位置观察雄萤火虫发出的闪光，在发现一个感兴趣趣的闪光后，雌性萤火虫会做出反应，发出闪光，求偶仪式就这样开始了。

一些雌性萤火虫会产生其他种类萤火虫的闪光模式，来诱捕雄性萤火虫并吃掉它们。

8.3萤火虫算法萤火虫算法模拟了萤火虫的自然现象。

真实的萤火虫自然地呈现出一种离散的闪烁模式，而萤火虫算法假设它们总是在发光。

为了模拟萤火虫的这种闪烁行为，Yang Xin-She提出了了三条规则（Yang，2009）[1]：1. 假设所有萤火虫都是雌雄同体的，因此一只萤火虫可能会被其他任何萤火虫吸引。

云计算下的基于萤火虫-遗传算法的资源调度单好民【摘要】如何能够最大限度发挥云计算中资源调度效率是目前研究的热点之一。

首先建立云计算环境下的资源调度模型，将萤火虫算法中的个体与云计算节点资源进行对应，其次在算法中个体初始化中引入遗传算法优化初始解，对算法中的位置更新设定感觉阀值用来调节个体选择最优路径的概率；最后针对挥发因子的改进使得荧光素的值进行更新。

仿真实验表明，该算法能够有效的提高云计算中的资源调度性能，缩短了任务完成的时间，提高系统整体处理能力。

%How to give the fullest play to the efficiency of resource scheduling in cloud computing is a hot spot of current research. First of all, resource scheduling model in cloud computing is established and individuals in firefly algorithm and node resources in cloud computing are matched; secondly, the genetic algorithm is introduced into the initialization of individuals in the algorithm and sensory threshold of the updating of algorithm’s position is set to adjust the probability for individuals to choose the optimal path; finally, the volatile factor is improved to update the value of fluorescein. Simulation experiment shows that this algorithm can effectively improve the performance of resource scheduling in cloud computing, shorten the time to complete tasks and improve the syste m’s overall processing capacity.【期刊名称】《计算机系统应用》【年(卷),期】2016(025)005【总页数】5页(P187-191)【关键词】云计算;萤火虫算法;遗传算法;资源调度【作者】单好民【作者单位】浙江邮电职业技术学院，绍兴 312000【正文语种】中文近年来, 云计算是集分布式计算、虚拟化技术、网格计算和Web服务等技术上发展起来的一种综合技术[1][2], 它通过互联网将处于网络中的各个节点的资源进行共享. 但如何能够最大限度的合理利用资源调度则是云计算研究的热门方向.目前, 国内外学者在云计算环境下的资源调度方面已经进行了大量研究工作, 文献[3]提出了在云计算中的使用一种基于改进粒子群优化算法, 利用PSO较快的收敛速度找到云资源调度问题的最优解, 并根据每个粒子的适应度值自适应地改变每个粒子的速度权重,提高了全局寻优能力和收敛能力, 仿真结果表明减少了任务的平均完成时间, 提高了任务处理的效率, 但粒子优化需要一定的时间; 文献[4]提出在整合虚拟云服务资源的基础上, 将模糊集理论引入到基于服务质量(QoS)的云服务资源选择中,取得了一定的效果, 但计算量大, 持续时间长; 文献[5]采用信息熵理论来维护非支配解集, 以保持解的多样性和分布均匀性; 在利用Sigma方法实现快速收敛的基础上, 引入混沌扰动机制, 以提高种群多样性和算法全局寻优能力, 避免算法陷入局部最优, 取得了比较好的效果, 但增加了算法的空间复杂性. 文献[6]提出了一种实现云计算负载均衡的双向蚁群优化算法(BACO)用于资源调度, 该算法考虑到了每个虚拟机的负载和计算能力, 同时在云环境中引入了蚂蚁的向前移动和向后移动, 结果表明该算法的总任务完成时间较短, 具有较好的寻优能力, 并且能够实现负载均衡,是一种有效的资源调度算法, 但增加了额外的硬件消耗; 文献[7]提出一种基于膜计算的蝙蝠算法, 将膜系统内部分解为主膜和辅助膜, 在辅助膜内进行蝙蝠的个体局部寻优, 将优化后的个体传送到主膜间进行全局优化, 从而达到了云计算资源优化分配要求, 实验表明算法提高了云计算环境下的系统处理时间和效率, 使得云计算环境下的资源分配更加合理, 其缺点是算法寻优过程复杂; 文献[8]提出一种面向应用性能的云计算弹性资源调整方法. 该方法利用自动伸缩算法, 在垂直层次上对负载需求的波动进行虚拟机资源调整, 以实现动态调整分配资源量来满足应用的服务级别的需求, 优化云计算资源利用率, 其缺点是容易受到需求波动影响; 文献[9]提出基于Q学习和双向ACO算法的云计算任务资源分配模型, 将其获得的最优策略对应的Q值初始化网络中节点的Q值, 算法能够实现任务资源的最终分配; 文献[10]提出一种低负载和低成本的资源分配策略, 实现系统负载均衡. 实验结果表明, 该策略在满足QoS约束的条件下, 有效地提高资源利用率, 其缺点是负载均衡无法控制; 文献[11]提出在云计算资源算法中引入安全机制, 保证资源传输过程中资源丢失; 文献[12]提出了一种结合请求率预测与能耗感知的弹性资源管理方法,以达到对系统能耗的弹性管理, 实验验证了该方法在保证服务质量的前提下能更有效地降低能耗, 其缺点是应用实践不足; 文献[13]提出从应用提供者收益角度考虑,兼顾SLA 收益损失和服务器租用成本投入, 提出虚拟机资源调度方法, 旨在使得应用租用者收益最大化, 实验证明取得了不错的效果, 其缺点是没有硬件损耗.本文针对萤火虫算法在资源调度方面的不足的基础上, 引入了遗传算法进行改进,使得改进后的算法在处理并行任务的资源分配方面有了进一步的提高,通过实验进一步证明了本文算法在云计算资源分配方面具有一定的优越性.云资源中的资源调度通过如下模型来表示:在公式(1)中,表示虚拟机的最大计算处理能力,表示作业包含的机器指令条数,表示任务最迟完工时间, 表示分配给任务的资源总和,表示为,其中是表示虚拟机占用计算资源总和. 表示为目标函数中效率函数, 根据云计算的资源调度的要求,云计算资源调度的最大化为.将云计算中的资源与萤火虫个体进行对应, 通过进一步优化萤火虫算法找到最有个体, 从而能够找到云计算中的资源分配方案.1.1 人工萤火虫算法假设萤火虫的群体为, 第只萤火虫所在的位置为, 第只萤火虫所对应的目标函数为, 第只萤火虫的萤光素的值为,表示第代的第个萤火虫的位置, 表示第代的第个萤光素的值, 萤火虫的视野范围更新如下:萤火虫个体位置更新公式:荧光素值的公式:1.2 遗传算法该算法是模拟遗传选择和自然淘汰的一种随机概率搜素算法. 其算法的组成主要包含4个步骤:(1) 数据编码方案的确定, 随机产生一个初始化个体;(2) 给出评价个体优劣的适应度值; 其中个体的评价是对每一个体计算其路径的长度, 并将该长度作为个体的适应度函数, 表示如下:式中,表示两个个体和之间的距离. 适应度越小的个体表示路径越短,则该个体越好.(3) 判断算法是否满足收敛的条件, 如果满足则输出搜素结果, 否则继续执行.(4) 分别按照交叉概率和变异概率来进行执行交叉操作.2.1 个体初始解的优化采用遗传算法来初始萤火虫个体的初始解,使得萤火虫算法的后期效率得到明显的提高. 设定萤火虫算法的种群大小为,将所有的萤火虫个体分为两个种群,分别为父种群和子种群. 其中父种群为,设定每一个个体的适应度函数为,子群(1) 变异操作: 第代种群中的第个个体依据公式(4)的变异方式.式(7)中的是变异后的种群中的个体, 为随机因子, 主要是用来控制差分向量的缩放程度, 设定值为[0,1]之间.(2) 交叉操作: 通过一定的概率选择, 将变异的中第个体与父代个体之间在第进行交叉, 得到新的个体式(8)中可以保证在交叉过程出现一个0到1之间的随机整数, 能够保证至少有一个分量来自.(3) 选择操作. 在进行选择个体使用“贪婪”选择策略, 使用适应度函数进行比较大小, 选择值大的个体进入下一代中, 即通过变异与交叉操作后生产的新的个体与上一代个体进行比较, 如果小于则保持不变, 否则直接进入下一代.通过上述三个步骤, 选取的个体为,将与子群进行合并, 使得. 然后将这些个体通过交叉, 变异等操作得到最后解, 作为萤火虫算法的初始解.2.2 阀值设定-个体的选择萤火虫个体在进行前进方向选择的策略是根据荧光素的值大小来进行判断, 这就容易导致在某一个方向上容易产生局部最优, 导致后续的萤火虫个体存在以较大的概率集中选择在当前局部最优的前进位置上, 为了避免这种情况的发生,设定一个阀值, 使得设定在路径上的荧光素的值小于阀值的时候,萤火虫个体可以忽略该前进方向的荧光素的值, 因此可以继续寻找. 反之, 萤火虫个体选择选择荧光素上的前进方向. 因此第只萤火虫个体按照以下的概率从状态到状态进行转换, 其中为状态列表. 2.3 针对的改进在公式(5)中, 由于荧光素更新公式中的发挥因子的作用, 使得没有在搜索路径上的荧光素的值逐步降低直至不被选择, 与此同时局部一些搜索路径上的发挥因子的值逐渐变大的时候, 有效解的信息量逐渐增大导致以前经过搜索的路径又重新参与全局路径的选择, 导致了降低了全局搜素最优能力个体解的降低,消耗了搜素的时间.因此应该对发挥因子的处理就显得尤为重要, 本文采用自适应的因子来改变的值, 设定的值初始值为0.99, 最小值为, 按照一定的循环次数进行逐渐递减;式中,是一个随机函数, 设定为自适应因子, 为循环次数,这种自适应因子可以保证在一定的搜素范围下的算法的全局搜索能力.2.4 算法步骤描述求解步骤如下, 流程如图1所示.Step1. 初始化萤火虫算法的各个参数, 设定种群数目, 算法迭代次数为, 最大次数为, 满足, 初始化萤火虫的个体位置, 定义合适的荧光素值;Step2. 针对云计算资源分配的特点, 将云计算节点的资源与萤火虫的个体位置进行一一对应;Step3. 根据3.1描述对萤火虫算法的个体进行初始化;Step4. 根据式(2)和(3)计算单个萤火虫的位置和荧光素的值, 找到各自目前节点的位置和荧光素的值.Step5. 根据式(4)(5)计算萤火虫最佳的位置, 然后根据式(7)(8)对萤火虫位置进行高斯变异更新, 在目前的位置上得到个体的新位置().Step6. 计算每一个萤火虫的,如果,则,否则再更新.Step7. 如果迭代次数小于, 转到Step8.Step8. 如果满足终止条件, 寻优过程便结束, 否则转向Step4继续优化.Step9. 根据萤火虫中的最优个体的位置变换为相应的云计算资源分配方案.为了进一步验证本文算法在云计算资源中调度的优越性, 本文从2个方面来进行比较:(1)与近几年发表的有关代表性的参考进行比较;(2)与经典的智能算法进行比较. 本文采用CloudSim[14]平台进行测试, 选择CPU为酷睿i3和4GDDR3, Windows Xp, 仿真软件采用matlab2012进行模拟.3.1与最近文献算法进行比较设定虚拟任务为400个,虚拟节点为100个, 设置迭代次数为300, 将本文的基于萤火虫-遗传算法和文献[3]和文献[10]的算法在云计算模型中不同任务数下进行比较.3.2 与经典的智能算法进行比较本文选取了云计算下的三种不同的虚拟任务情况下的算法运行效果对比. 分别选取了任务数为1000,任务数为10万和任务数为100万作为研究对象.(1) 虚拟任务为1000的算法性能对比采用遗传算法、萤火算法、本文算法对任务为1000和资源数量为100进行分配, 比较结果如图4所示. 从图4可以发现任务数量在400左右成为了分界点, 完成之前三种算法相差不大. 分界点之后三种算法之间才出现区别, 基本上满足云计算条件下的资源分布.(2) 虚拟任务为10万的算法性能对比采用遗传算法、萤火算法、本文算法对任务为10万和资源数量为1000进行分配, 比较结果如图5所示. 从图5可以发现任务数量开始的阶段就区分开来, 并且本文算法与萤火虫算法在开始阶段相差不大, 伴随着任务数量逐渐增大, 三种算法呈现比较大的区别, 本文的算法适合在云计算条件下的虚拟任务较大的资源调度问题.(3) 虚拟任务为100万的算法性能对比采用遗传算法、萤火算法、本文算法对任务为100万和资源数量为1000进行分配, 比较结果如图6所示. 从图6可知, 随着虚拟任务数增加, 当任务数达到50万的时候, 本文的算法的任务完成时间要远远少于其他, 主要是原因是因为算法中进行了个体初始化以及采用了阀值来设定和针对进行了改进. 本文的算法适合在非常适合云计算条件下的虚拟任务非常大的资源调度问题, 效果越明显.通过建立云计算环境下的资源调度模型, 将萤火虫算法中的个体与云计算节点资源进行对应, 其次在算法中个体初始化中引入遗传算法优化初始解, 对算法中的位置更新设定感觉阀值用来调节个体选择最优路径的概率;最后针对挥发因子的改进使得荧光素的值进行更新. 通过实验证明, 本文算法能够有效满足云计算资源分配模型, 为云计算资源分配提供了一定的参考价值.1 李乔,郑啸.云计算研究现状综述.计算机科学,2011,38(4): 32-37.2 葛新.基于云计算集群扩展中的调度问题研究[学位论文].合肥:中国科学技术大学,2011.3 蔡琪,单冬红,赵伟艇.改进粒子群算法的云计算环境资源优化调度.辽宁工程技术大学学报(自然科学版),2015,35(1):93-96.4 Wang S, Dey S. Rendering adaptation to address communication and computation constraints in cloud mobile gaming. 2010 IEEE Global Telecommunications Conference (GLOBECOM 2014). IEEE. 2010. 1-6.5 张恒巍,韩继红,卫波,王晋东.基于Map-Reduce模型的云资源调度方法研究.计算机科学,2015,42(8):118-123.6 王常芳,徐文忠.一种用于云计算资源调度的双向蚁群优化算法.计算机测量与控制,2015,23(8):2861-2863.7 宁彬,谷琼,吴钊,袁磊,胡春阳.基于膜计算的蝙蝠算法在云计算资源调度的研究.计算机应用研究,2015,32(3):b 830-833.8 申京,吴晨光,郝洋.面向云计算数据中心的弹性资源调整方法.南京理工大学学报(自然科学版),2015,39(1):89-93.9 孙花,朱锦新.基于Q学习和双向ACO算法的云计算任务资源分配模型设计.计算机测量与控制,2014,22(10): 3343-3347.10 方义秋,郑剑,葛君伟.一种云环境下基于QoS约束的资源分配策略.计算机应用与软件,2015,32(1):34-38.11 Liang H, Huang D, Cai L X, et al. Resource allocation for security services in mobile cloud Computing. IEEE Conference on ComputerCommunications Rkshops. IEEE. 2014, 12. 191-195.12 熊伟,李兵.云计算环境下基于能耗感知的弹性资源管理机制.四川大学学报(工程科学版),2015,47(2):112-116.13 叶世阳,张文博,钟华.一种面向SLA的云计算环境下虚拟资源调度方法.计算机应用与软件,2015,32(4):11-17.14 Calheiros RN, Ranjan R, Caf de R, Buyya R. CloudSim: A novel framework for modelingand simulation of cloud computing infrastructures and services. arXiv:0903.2525. [2009-9-3].。

萤火虫算法参数分析与优化卓宏明; 陈倩清【期刊名称】《《微型机与应用》》【年(卷),期】2019(038)011【总页数】7页(P60-66)【关键词】萤火虫算法; 参数分析; 数值试验【作者】卓宏明; 陈倩清【作者单位】浙江国际海运职业技术学院船舶工程学院浙江舟山316021【正文语种】中文【中图分类】TP301.60 引言萤火虫算法Firefly Algorithm(FA)是2008年YANG X S[1-2]提出的一种新型群智能优化算法，其操作简单、参数少、易实现，成为众多学者研究的热点，在诸多领域得到了较好的应用[3-6]。

然而决定算法性能的参数选择还缺少相关的深入研究，算法的参数设定对求解性能影响很大，因此，萤火虫算法的参数优化已成为急需解决的问题。

1 萤火虫算法及数学模型萤火虫算法基本思想是模拟萤火虫的发光特性在一定区域内寻找伙伴，向位置较优的萤火虫移动，以达到寻优的目的。

将问题的目标函数定义为萤火虫所处位置的适应度值，将优化过程模拟成萤火虫个体的相互吸引而引发的位置更新的过程，将个体的优胜劣汰过程类比为搜索和优化过程中用好的可行解取代较差可行解的迭代过程。

萤火虫算法的寻优主要由荧光亮度和吸引度两个关键要素实现。

主要公式包括相对相对萤光亮度公式、相对吸引度公式和位置更新公式[1-2]，如下所示：萤火虫的相对萤光亮度为：I=I0×e-γrij(1)其中，I0 为初始光强度，即在光源(r=0)处的光强度，与目标函数值相关，目标函数值越优自身亮度越高；γ为光强吸收系数即吸收因子，以体现光强的减弱特性，一般情况下γ∈[0.01，100]；r 通常为萤火虫i与j间的欧氏距离。

萤火虫的吸引度为：(2)其中，β0为最大吸引力，即光源(r=0)处的吸引力。

萤火虫i被萤火虫j吸引而向其移动的位置更新公式如下：xj(t+1)=xj(t)+βij(rij)[xi(t)-xj(t)]+αεj(3)其中，t为算法迭代次数；α为随机步长，一般取值范围为[0，1]；εj通常是由高斯分布、均匀分布或其他分布生成的随机数向量。

萤火虫算法在化工过程优化中的应用摘要：近些年以来，以萤火虫算法为代表的群智能优化算法由于具有强大的寻优功能而得到了广泛的应用。

在化工生产的过程中，采用萤火虫算法和Matlab 语言对实际问题进行优化的同时还采用了苯-甲苯闪蒸过程对其进行了仿真计算。

仿真结果表明，气相产物中苯的产量在有效的调节温度、压力以及分流系数的条件下能够达到最大，不仅实现了苯-甲苯闪蒸过程的最优化，同时还充分证明了在解决化工生产过程的优化问题上采用萤火虫算法是有效的。

Abstract: In recent years, the swarm intelligence optimization algorithm represented by the firefly algorithm with powerful optimizationseeking function has been widely used. In the process of chemical production, the actual problems are optimized by firefly algorithm andMatlab language, at the same time, and the simulation calculation is carried out by benzene-toluene flash process. The simulation resultsshow that the output of benzene in the gaseous phase products can achieve maximum under the condition of effective regulation oftemperature, pressure, and shunt coefficient, which not only realized the optimization of benzene-toluene flash process, but also fullydemonstrated that it's effective to solve the optimization problem in the process of chemical production with the firefly algorithm.关键词：苯-甲苯；闪蒸过程；萤火虫算法；优化仿真Key words: benzene-toluene；flash process；firefly algorithm；optimization simulation中图分类号：TQ202 文献标识码院A 文章编号院1006-4311（2014）24-0303-020 引言许多化工过程中定态优化问题都属于非线性约束问题，在对其进行解决的时候通常采用常规经典数学方法，如广义梯度法和逐次二次规划法等。

matlab智能算法代码MATLAB是一种功能强大的数值计算和科学编程软件，它提供了许多智能算法的实现。

下面是一些常见的智能算法及其在MATLAB中的代码示例：1. 遗传算法（Genetic Algorithm）：MATLAB中有一个专门的工具箱，称为Global Optimization Toolbox，其中包含了遗传算法的实现。

以下是一个简单的遗传算法示例代码：matlab.% 定义目标函数。

fitness = @(x) x^2;% 设置遗传算法参数。

options = gaoptimset('Display', 'iter','PopulationSize', 50);% 运行遗传算法。

[x, fval] = ga(fitness, 1, options);2. 粒子群优化算法（Particle Swarm Optimization）：MATLAB中也有一个工具箱，称为Global Optimization Toolbox，其中包含了粒子群优化算法的实现。

以下是一个简单的粒子群优化算法示例代码：matlab.% 定义目标函数。

fitness = @(x) x^2;% 设置粒子群优化算法参数。

options = optimoptions('particleswarm', 'Display','iter', 'SwarmSize', 50);% 运行粒子群优化算法。

[x, fval] = particleswarm(fitness, 1, [], [], options);3. 支持向量机（Support Vector Machine）：MATLAB中有一个机器学习工具箱，称为Statistics and Machine Learning Toolbox，其中包含了支持向量机的实现。

%% 算法说明：荧火虫算法clc; %清屏clear all; %清除变量format long; %确定精度%% 各参数初始化开始domx=[-5.12,5.12;-5.12,5.12];% domx=[-2.048,2.048;-2.048,2.048]; %解空间rho=0.4; %荧光素挥发因子gamma=0.6; %适应度提取比例beta=0.08; %邻域变化率nt=5; %邻域阀值(邻域荧火虫数)s=0.03; %步长lo=5; %荧光素浓度rs=5.12; %感知半径r0=5.12;% rs=2.048; %感知半径% r0=2.048; %决策半径%各参数初始化结束iter_max=200; %最大迭代次数%% 分配空间开始m=size(domx,1); %函数空间维数global n;n=50; %种群规模address=zeros(n,m); %分配荧火虫地址空间value=zeros(n,1); %分配适应度存放空间li=zeros(n,1); %分配荧光素存放空间rdi=zeros(n,1); %分配荧火虫决策半径存放空间uu=zeros(1,iter_max);%% 荧火虫常量初始化开始for i=1:maddress(:,i)=(domx(i,1)+(domx(i,2)-domx(i,1))*rand(n,1)); %初始化地址% address(i,:)=5*rands(n,1); %随机产生初萤火虫所在位置endf=fun(address);x=-5.12:.1:5.12;% x=-2.048:.05:2.048;[x,y] = meshgrid(x);figure(1);plot3(address(:,1),address(:,2),f,'k*')hold on;grid on;z=-(x.^2-10*cos(2*pi.*x)+10+y.^2-10*cos(2*pi.*y)+10); %Rastrigin'函数% z=-(x.^2+y.^2); %目标函数J2% z=-(20+x.^2-10*cos(2*pi.*x)+y.^2-10*cos(2*pi.*y)); %目标函数J1% z=-(-20*exp(-0.2*sqrt((x.^2+y.^2)/2))-exp((cos(2*pi*x)+cos(2*pi*y))/2)+20+exp(1)); %%目标函数% z=-(0.5+sin(sqrt(x.^2 + y.^2).^2-0.5)./(1+0.001*(x.^2 + y.^2)).^2);%目标函数J3mesh(x,y,z)xlabel('x轴');ylabel('y轴');zlabel('z轴');title('萤火虫初始分布图');li(:,1)=lo; %荧光素初始值rdi(:,1)=r0; %决策半径初始值t=1; %迭代累计量%荧火虫常量初始化结束%% 迭代开始while(t<=iter_max)li=(1-rho)*li+ gamma * fun(address); %.更新荧光素值li%各荧火虫移动过程开始for i=1:nOrd_number=[]; %存放荧火虫序号for j=1:nif (norm(address(j,:)-address(i,:))<rdi(i)) && (li(i,1)<li(j,1)) %决策半径内找更优点Ord_number(numel(Ord_number)+1)=j;endend%计算Ord_number各元素被选择概率，确定j位置if ~isempty(Ord_number) %先判断Ord_number个数不为空Ord_num_li=li(Ord_number,1); %选出Ord_number荧光素Sum_Ord_li=sum(Ord_num_li); %Ord_number荧光素和Mol=Ord_num_li-li(i,1); %分子(lj-li)Den=Sum_Ord_li-li(i,1); %分母Pij=Mol./Den; %计算各元素被选择概率Pij=cumsum(Pij); %累计Pij=Pij./Pij(end); %归一化Pos=find(rand<Pij); %确定位置j=Ord_number(Pos(1)); %确定j 的位置%荧火虫i向位置j移动address(i,:)=address(i,:)+ s*(address(j,:)-address(i,:))/norm(address(j,:)-address(i,:));address(i,:)=range1(address(i,:),domx);%限制范围end%更新决策半径rdi(i)=rdi(i)+beta*(nt-length(Ord_number));rdi(i)=min(rs,max(0,rdi(i)));uu(t)=-max(fun(address));endt=t+1;% iter_max迭代结束g=[];g=fun(address);x=-5.12:.1:5.12;% x=-2.048:.05:2.048;[x,y] = meshgrid(x);figure(2);plot3(address(:,1),address(:,2),g,'k*');hold on;z=-(x.^2-10*cos(2*pi.*x)+10+y.^2-10*cos(2*pi.*y)+10); %Rastrigin'函数% z=-(x.^2+y.^2);%目标函数J2% z=-(20+x.^2-10*cos(2*pi*x)+y.^2-10*cos(2*pi*y)); %目标函数J1% z=-(-20*exp(-0.2*sqrt((x.^2+y.^2)/2))-exp((cos(2*pi*x)+cos(2*pi*y))/2)+20+exp(1)); %%目标函数% z=-(0.5+sin(sqrt(x.^2 + y.^2).^2-0.5)./(1+0.001*(x.^2 + y.^2)).^2);%目标函数J3grid on;mesh(x,y,z);title('萤火虫运动轨迹');xlabel('x轴');ylabel('y轴');zlabel('z轴');hold off;endfigure('name','收敛曲线');plot(uu)title(['萤火虫最优值曲线' '终止次数＝' num2str(iter_max)]);xlabel('迭代次数');ylabel('最优值');%% 输出最优结果value=fun(address);disp('最优值为：')num=find(value==max(value));%最大值序号MaxValue=-max(value)disp('最优解为：')BestAddress = address(num,:)%目标函数function y = fun(x)% y=x(:,1).^2+x(:,2).^2;% y=0.5+sin(sqrt(x(:,1).^2 + x(:,2).^2).^2-0.5)./(1+0.001*(x(:,1).^2 + x(:,2).^2)).^2;%目标函数J3 % y=20+x(:,1).^2-10*cos(2*pi*x(:,1))+x(:,2).^2-10*cos(2*pi*x(:,2)); %目标函数J1% y=-20*exp(-0.2*sqrt((x(:,1).^2+x(:,2).^2)/2))...% -exp((cos(2*pi*x(:,1))+cos(2*pi*x(:,2)))/2)+20+exp(1); %%目标函数y=x(:,1).^2-10*cos(2*pi.*x(:,1))+10+x(:,2).^2-10*cos(2*pi.*x(:,2))+10; %Rastrigin'函数y=-y;。