一维对流扩散问题求解

一维对流扩散方程的格子Boltzmann模型研究雷娟霞;李春光【摘要】给出了一维对流扩散方程(e)u/(e)t+α(e)u/(e)x=β(e)2u/(e)x2的一种三速格子Botzmann模型(D1Q3模型).采用Chapman-Enskog多尺度展开技术,导出了该模型的平衡态分布函数.理论分析和数值算例均表明,该模型方法具有计算量小、精度较高等特点.【期刊名称】《宁夏工程技术》【年(卷),期】2018(017)003【总页数】4页(P218-221)【关键词】格子Boltzmann方法;对流扩散方程;Chapman-Enskog展开;平衡态分布函数;数值模拟【作者】雷娟霞;李春光【作者单位】北方民族大学数学与信息科学学院,宁夏银川 750021;北方民族大学数值计算与工程应用研究所,宁夏银川 750021【正文语种】中文【中图分类】O242.1对流扩散方程在数学物理领域扮演着非常重要的角色。

近年来，关于这类方程的一些数值模拟方法逐渐发展起来，包括有限差分法[1—2]、有限元法[3]、有限体积法[4]等。

然而，由于对流扩散方程求解的复杂性，传统的数值模拟方法很难对其进行有效模拟。

格子 Boltzmann 方法（Lattice Boltzmann method，简称LBM）不同于传统的数值方法，它是介于宏观和微观的介观方法。

LBM在求解非线性偏微分方程，特别是在流体力学的研究中取得了很大成果，这是由于LBM具有物理背景清晰、边界容易处理、编程实现简单等优点。

LBM提供了联系宏观和微观的可能性和现实性，除了在一般的流体力学问题中得到了成功的验证之外，在湍流[5—6]、多相流[7]、粒子悬浮流[8]等相关领域也具有广阔的应用前景。

本文利用LBM构造了一个D1Q3模型，该模型具有3个速度方向，平衡态分布函数的最小量也展开到三阶。

本文给出了详细的理论推导，同时用数值算例验证了模型的有效性。

1 模型及方法1.1 一维对流扩散方程考虑如下一维对流扩散方程：式中：α，β为常数为对流项为扩散项。

一维对流扩散方程是指一维均匀的边界层上的传质过程的数学模型，常用于描述对流扩散过程中的温度、湿度、速度等场的分布情况。

一维对流扩散方程的数学形式为：∂φ/∂t+U∂φ/∂x=D∂^2φ/∂x^2其中φ表示传质物质的浓度，t表示时间，x表示空间坐标，U表示对流速度，D表示扩散系数。

二维对流扩散方程是指二维均匀的边界层上的传质过程的数学模型，常用于描述对流扩散过程中的温度、湿度、速度等场的分布情况。

二维对流扩散方程的数学形式为：∂φ/∂t+U∂φ/∂x+V∂φ/∂y=D∂^2φ/∂x^2+D∂^2φ/∂y^2其中φ表示传质物质的浓度，t表示时间，x和y分别表示两个空间坐标，U和V分别表示两个方向上的对流速度，D表示扩散系数。

单调差分格式是一种常用的数值求解方法，它通过进行差分运算来求解微分方程的数值解。

在求解一维和二维对流扩散方程时，可以使用单调差分格式来解决。

具体来说，可以将空间坐标和时间分别离散化，将对流扩散方程转化为一个线性方程组，然后使用单调差分格式来解决。

单调差分格式的具体形式取决于方程的类型和离散化的方式，但一般来说，它都是将微分方程的差分形式写成一个线性方程组的形式。

例如，在求解一维对流扩散方程时，可以使用下面的单调差分格式：φ_i^{n+1}=φ_i^n+Δt(D(φ_{i+1}^n-2φ_i^n+φ_{i-1}^n)/Δx^2+U(φ_ {i+1}^n-φ_{i-1}^n)/2Δx)其中φ_i^n表示第i个网格点在时间步n的浓度值，Δx和Δt分别表示网格的空间步长和时间步长。

同样的，在求解二维对流扩散方程时，可以使用下面的单调差分格式：φ_i^n=φ_i^n+Δt(D(φ_{i+1,j}^n+φ_{i-1,j}^n+φ_{i,j+1}^n+φ_{i,j-1}^ n-4φ_i^n)/Δx^2+U(φ_{i+1,j}^n-φ_{i-1,j}^n)/2Δx+V(φ_{i,j+1}^n-φ_ {i,j-1}^n)/2Δy)其中φ_i^n表示第(i,j)个网格点在时间步n的浓度值，Δx和Δy分别表示网格在x和y方向上的空间步长，Δt表示时间步长。

对流方程及其解法对流方程是描述流体运动的最基本方程之一，涉及热、动量、物质等的传递现象，对于各种物理问题的研究都具有重要意义。

本文将从对流方程的基本形式和意义出发，探讨其常见解法及相关应用。

一、对流方程的基本形式与意义对流方程是描述流体中质量、热量和动量传递的方程，其基本形式可以写作：$$ \frac{\partial\phi}{\partial t} + (\mathbf{v}\cdot\nabla)\phi =\nabla\cdot(\Gamma\nabla\phi) $$其中，$\phi$为描述流体量的变量，如温度、密度、浓度等；$\mathbf{v}$为流体的流速，$\Gamma$为扩散系数。

对该方程的解析求解较为困难，故通常采用数值方法进行求解。

下面介绍几种常见的数值解法。

二、有限差分法有限差分法是在连续方程的基础上，利用有限差分代替导数，将微分方程变为代数方程组，从而利用计算机求解的方法。

其基本思想是将求解区域划分为有限个网格，对每个网格内的量用差分代替导数，从而得到有限差分方程。

以简单的二维对流扩散为例，其对流方程为：$$ \frac{\partial\phi}{\partial t} + u\frac{\partial\phi}{\partial x} + v\frac{\partial\phi}{\partial y} = \Gamma\frac{\partial^2\phi}{\partial x^2} + \Gamma\frac{\partial^2\phi}{\partial y^2} $$其中，$u$和$v$分别代表$x$和$y$方向的流速。

对该方程进行离散，假设$\phi_{i,j}$为$x=i\Delta x$，$y=j\Delta y$处的$\phi$值，则可以得到：$$ \frac{\phi^{k+1}_{i,j} - \phi^k_{i,j}}{\Delta t} +u\frac{\phi^k_{i+1,j} - \phi^k_{i-1,j}}{2\Delta x} +v\frac{\phi^k_{i,j+1} - \phi^k_{i,j-1}}{2\Delta y} $$$$ = \frac{\Gamma\Delta t}{(\Delta x)^2}(\phi^k_{i+1,j} -2\phi^k_{i,j} + \phi^k_{i-1,j}) + \frac{\Gamma\Delta t}{(\Deltay)^2}(\phi^k_{i,j+1} - 2\phi^k_{i,j} + \phi^k_{i,j-1}) $$其中，$k$为时刻，$\Delta x$和$\Delta y$分别为$x$和$y$方向的网格间距。

一维对流扩散问题例题含吸附作用一维对流扩散问题是描述物质在一维空间中传输的数学模型。

吸附作用是指物质在传输过程中与固体表面发生相互作用，被固体吸附的现象。

下面是一个关于一维对流扩散问题含吸附作用的例题：假设有一根长度为L的管道，管道内充满了某种气体。

气体沿管道的方向发生对流传输和扩散，同时在管道壁上发生吸附作用。

已知管道的吸附速率常数为k，气体的对流速度为u，扩散系数为D。

求解以下问题：1. 假设管道内初始时刻气体浓度均匀分布，求解在稳态情况下管道内吸附物质的分布。

2. 假设管道内初始时刻气体浓度为C0，求解在稳态情况下管道内气体浓度随时间和位置的变化。

解答：1. 在稳态情况下，管道内吸附物质的分布可以通过解一维扩散方程和吸附方程的组合得到。

扩散方程为：∂C/∂t = D * ∂²C/∂x²吸附方程为：∂θ/∂t = -k * θ其中，C是气体浓度，θ是吸附物质的分布，t是时间，x是空间位置。

根据稳态条件，扩散方程右侧为0，可以得到：∂²C/∂x² = 0对扩散方程积分两次得到：C(x) = Ax + B再根据吸附方程，可以得到：θ(t) = Ce^(-kt)其中A、B和C是待定系数，可以利用边界条件来确定。

边界条件可以是在管道起始端和末端的浓度值或者通量值。

求解稳态问题时，通常会假设管道起始端浓度已知，末端处的吸附物质浓度为零。

2. 在稳态情况下，气体浓度随时间和位置的变化可以通过解一维扩散方程得到。

扩散方程为：∂C/∂t = D * ∂²C/∂x²根据稳态条件，扩散方程右侧为0，可以得到：∂²C/∂x² = 0对扩散方程积分一次得到：∂C/∂x = A再次积分得到：C(x) = Ax + B其中A和B是待定系数，根据边界条件可以确定A和B的值。

边界条件可以是在管道起始端和末端的浓度值或者通量值。

通过上述方法，可以求解一维对流扩散问题含吸附作用的例题。

Sinc-Chebyshev配置方法求解一维对流扩散方程毛志【摘要】利用复合移位Sinc函数和移位Chebyshev多项式,构造了求解变系数的一维对流扩散方程初边值问题的Sinc-Chebyshev配置方法.【期刊名称】《铜仁学院学报》【年(卷),期】2013(015)005【总页数】4页(P146-149)【关键词】Sinc函数;移位Chebyshev多项式;Sinc-Chebyshev配置方法;变系数的对流扩散方程【作者】毛志【作者单位】铜仁学院数学与计算机科学系,贵州铜仁554300【正文语种】中文【中图分类】O241.82一、引言对流扩散方程（convection diffusion equation）是一类基本的运动方程，是描述粘性流体的非线性方程的线性化模型方程。

它可以用来描述空气动力学、水力学、环境保护和生物、化学工程等众多科技和工程领域中的对流扩散问题[1]，所以关于对流扩散方程数值方法的研究具有十分重要的理论价值和现实意义。

对流扩散问题的有效数值解法一直是计算数学中重要的研究内容。

由于对流扩散方程同时含有对流项和扩散项，在数值求解时会引起数值振荡和数值弥散[2]，使得方程的求解比较复杂。

目前，求解对流扩散方程的数值方法有多种，如有限差分法（FDM）[3]、有限元法（FEM）[4][5]、有限体积法（FVM）[6][7]、边界元法（BEM）等，其中有限差分方法是一种重要的数值计算方法。

目前对于常系数的对流扩散方程已有较多、较好的研究，而对于变系数的对流扩散方程的研究却较少，需要对方程做一定的假设。

但在实际应用中，比如耦合流场的对流扩散方程，则需要研究变系数的情形[8]。

基于此，本文考虑如下变系数的一维对流扩散方程的初边值问题，其中a（x,t）、b（x,t）、f（x,t）和g（x）已知，a（x,t ）≠0、 b （x,t ）≠ 0 且连续。

本文设计了一种新的求解上述问题（1）～（3）的数值方法---Sinc-Chebyshev配置方法。

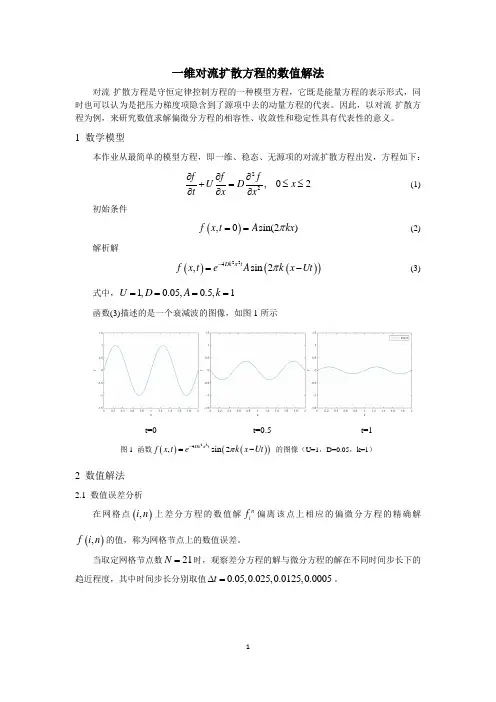
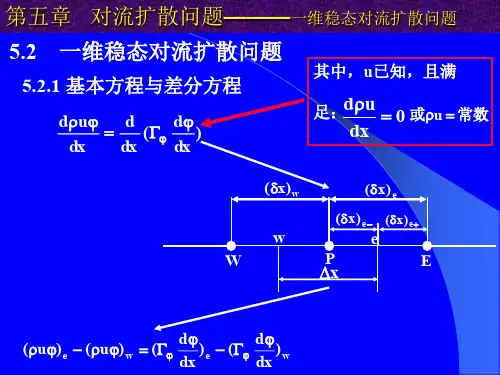
一维对流扩散方程的数值解法对流-扩散方程是守恒定律控制方程的一种模型方程，它既是能量方程的表示形式，同时也可以认为是把压力梯度项隐含到了源项中去的动量方程的代表。

因此，以对流-扩散方程为例，来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。

1 数学模型本作业从最简单的模型方程，即一维、稳态、无源项的对流扩散方程出发，方程如下： 22, 02f f fU D x t x x∂∂∂+=≤≤∂∂∂ (1)初始条件 (),0sin(2)f x t A kx π==(2)解析解()()()224,sin 2Dk tf x t eA k x Ut ππ-=-(3)式中，1,0.05,0.5,1U D A k ====函数(3)描述的是一个衰减波的图像，如图1所示t=0 t=0.5 t=1图1 函数()()()224,sin 2Dk tf x t ek x Ut ππ-=- 的图像（U=1，D=0.05，k=1）2 数值解法2.1 数值误差分析在网格点(),i n 上差分方程的数值解ni f 偏离该点上相应的偏微分方程的精确解(),f i n 的值，称为网格节点上的数值误差。

当取定网格节点数21N =时，观察差分方程的解与微分方程的解在不同时间步长下的趋近程度，其中时间步长分别取值0.05,0.025,0.0125,0.0005t ∆=。

（a ）21,0.05N t =∆= （b ）21,0.025N t =∆=（c ）21,0.0125N t =∆= （d ）201,0.0005N t =∆=图2 数值误差随步长的变化情况从图2的(a)~(d)可以定性的看出，数值误差与步长的大小有关。

在满足稳定性条件的前提下，数值误差随着时间步长的减小而减小，同时，图（d ）表示增大网格的分辨率也有助于减小网格误差。

为了对数值误差有一个定量的认识，接下来取定时间步长为0.0005t ∆=，分别算出11,21,41,61,81,101,121,161N =时，指标E =1所示。