三角形等积变形 Microsoft Office PowerPoint 演示文稿 2

第三讲等积变形
第三讲等积变形
思考一：三角形按角度大小课分为哪几类？三角形的面积怎噩梦计算？一个三角形有几个底几个高？你会作三角形的高吗？（尤其是钝角三角形的高）
思考二：三角形的高不变，底变，面积会不会变？怎么变？反过来呢？
思考三：你能把一个三角形分成面积相等的两份吗？如果是三份、四份……n份你还会吗？
（想想还有别的分法么？）
思考四：找等高三角形
例如在上图中，若以BC所在的直线为底，发现∆
,为等高三角形，你能找出思考三中画出的三∆,
ABD∆
ABC
ADC
角形中有哪些等高三角形吗？
思考五：你会画辅助线吗？什么时候需要画辅助线？该怎么画辅助线呢？（例3，例4，例5）
（辅助线的做法：找到有倍数关系的边，以它们所在的直线为底，找等高三角形）
思考六：你还记得一半模型吗？如果变一变你还会吗？（提高学案四）
思考七：（1）下面平行线间的三个三角形有什么关系呢？
（2）下面梯形中有几组三角形面积相等，你能找出来
吗？
思考八：两个并排的正方形，同方向的一组对角线平行吗？阴影部分的面积怎么求？（例6，尖子班学案4，超常挑战）。

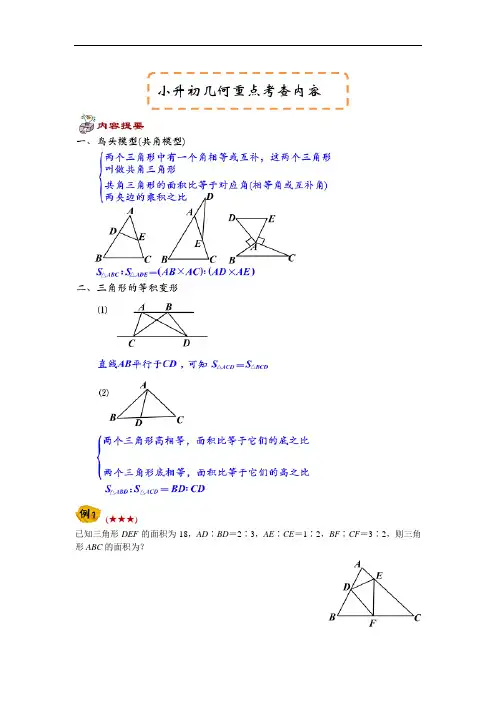
(★★★)已知三角形DEF的面积为18，AD∶BD＝2∶3，AE∶CE＝1∶2，BF∶CF＝3∶2，则三角形ABC的面积为？小升初几何重点考查内容(★★★)如图，已知三角形ABC面积为1，延长AB至D，使BD＝AB；延长BC至E，使CE＝2BC；延长CA至F，使AF＝3AC，求三角形DEF的面积。

(★★★★)如图将四边形ABCD四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H，若四边形ABCD的面积为5cm2，则四边形EFGH的面积是多少？(★★★)图中三角形ABC的面积是180平方厘米，D是BC的中点，AD的长是AE长的3倍，EF的长是BF长的3倍。

那么三角形AEF的面积是多少平方厘米(★★★★)如图，大长方形由面积是12平方厘米、24平方厘米、36平方厘米、48平方厘米的四个小长方形组合而成。

求阴影部分的面积。

(★★★★★)(2009年“学而思杯”六年级)如图BC＝45，AC＝21，△ABC被分成9个面积相等的小三角形，那么DI＋FK＝_____。

在线测试题温馨提示：请在线作答，以便及时反馈孩子的薄弱环节。

1．★★★★设111,,,345AD AB BE BC FC AC===如果三角形DEF的面积为19平方厘米，那么三角形ABC的面积是多少平方厘米？A．46.7 B．45.3 C．45.6 D．46.5FEDCBA2．★★★如下图，将三角形ABC 的BA 边延长1倍到D ，CB 的边延长2倍到E ，AC 边延长1倍到F 。

如果三角形ABC 的面积等于1，那么三角形DEF 的面积是多少？ A ．10 B ．8 C ．9 D ．11EFDCBA3．★★★★★如图，把四边形ABCD 的各边都延长3倍，得到一个新四边形EFGH ，如果ABCD 的面积是6，则EFGH 的面积是( )? A ．130 B ．145 C ．160 D ．1504．★★★★如图， D 是BC 的中点，AD 的长是AE 长的3倍，EF 的长是BF 长的3倍．三角形AEF 的面积是18平方厘米，三角形ABC 的面积是( )平方厘米？ A ．144 B ．168 C ．72 D ．1005．★★图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是( ) A ．50 B ．48 C ．56 D ．45EGC B6．★★★如图，1ABC S =△，5BC BD =，4AC EC =，DG GS SE ==，AF FG =。

三角形等积变形
三角形是几何学中的一个基本形状，具有三条边和三个角。

在数学中，我们学习过三角形的性质和各种定理，但在生活中，三角形的形状也经常出现在我们的眼前。

而在艺术中，三角形等积变形是一种常见的设计元素，可以为作品增添美感和动感。

在建筑设计中，三角形等积变形常常被用来设计建筑的外观和结构。

例如，许多现代建筑采用了三角形的形状，不仅可以增加建筑的美感，还可以提高建筑的稳定性和结构强度。

这种设计不仅具有美学上的价值，还具有实用性，体现了建筑师对结构和功能的兼顾。

在艺术作品中，三角形等积变形也经常被运用。

艺术家们通过将三角形等积变形组合在一起，创造出各种美丽的图案和设计。

这些作品不仅具有装饰性，还可以传达出艺术家的情感和思想。

三角形等积变形的组合可以产生无穷无尽的可能性，让人们在欣赏作品的同时，感受到艺术家的创意和灵感。

在日常生活中，三角形的形状也随处可见。

比如，许多家具和装饰品都采用了三角形的设计，为家居空间增添动感和现代感。

此外，一些日常用品如餐具、文具等也常常采用三角形的形状，方便使用的同时也美观大方。

总的来说，三角形等积变形在各个领域都有着重要的作用。

无论是在建筑设计、艺术创作还是日常生活中，三角形的形状都能给人带
来美的享受和视觉上的愉悦。

通过运用三角形等积变形，人们可以创造出无限的可能性，展现出自己的创意和想象力。

让我们一起欣赏和探索三角形等积变形的魅力，感受美的力量和无限的可能性。

胜利教育教案教学内容第十讲三角形的等积变形授课类型新授所需时间110分教学时间教学目标：知识目标：利用三角形的面积与底和高关系解决稍复杂的图形。

能力目标：培养学生的观察，分析能力。

情感目标：激发学习的斗志和情趣。

教学重点及教学难点:重点及难点：利用三角形的面积与底和高的关系解决稍复杂的图形。

教学方法讲授法教具准备教师活动学生活时间动一、引入:回顾：1、两个三角形底(高)相等,高(底)成几倍关系？面积成几倍关系？2、等底等高的的两三角形的面积相等。

二、新授：1、出示例1分析：看图，根据所给的条件作辅助线。

解法一：连接BD，在ΔABD中：∵ BE=3AE∴SΔABD=4SΔADB=4cm2在ΔABC中，∵ CD=2AD又∵SΔADB=SΔABC-SΔBDCSΔABC=3SΔABD=3×4=12cm2解法二：略作业：P36 7２题2、出示例2：分析：连接ＢＧ，在ΔＡＢＧ中：∵ BＤ=２ＡＤ∴SΔＡＤＧ＝１/３SΔＡＢＧ在SΔＡＢＣ中ＡＧ＝２ＣＧ∴SΔＡＢＧ＝２/３SΔＡＢＧ∴SΔＡＤＧ＝１/３×２/３SΔＡＢＧ＝２/９ＳΔABC同理：ＳΔＢＤＥ＝１/９SΔＡＢＣSΔＣＦＧ＝１/９SΔＡＢＣSΔＡＤＧ＋SΔＢＤＥ＋SΔＣＦＧ＝（２/９＋２/９＋１/９）SΔＡＢＣ＝５/９SΔＡＢＣ阴影部分面积＝（１－５/９）SΔＡＢＣ＝４/９SΔＡＢＣ作业：Ｐ３６７１例３：分析：连接ＡＦ、CF∴SΔADE=SΔＡCESΔCDF=∴SΔＡCF又∵ AC与EF平行∴SΔACE=SΔＡCF∴SΔADE=SΔCDF=4cm2作业：P36 74例4:分析：连接AC，∵ AB∥CD∴SΔADE=SΔACE而SΔACF=SΔACE+SΔAEFSΔABF=SΔBEF+SΔAEF∴SΔACE=SΔBEF∴SΔBEF=SΔADE=1cm2三、总结四、作业板书设计:三角形等积变形(二)例1------------------------- 例2------------------------- 例3-------------------------。

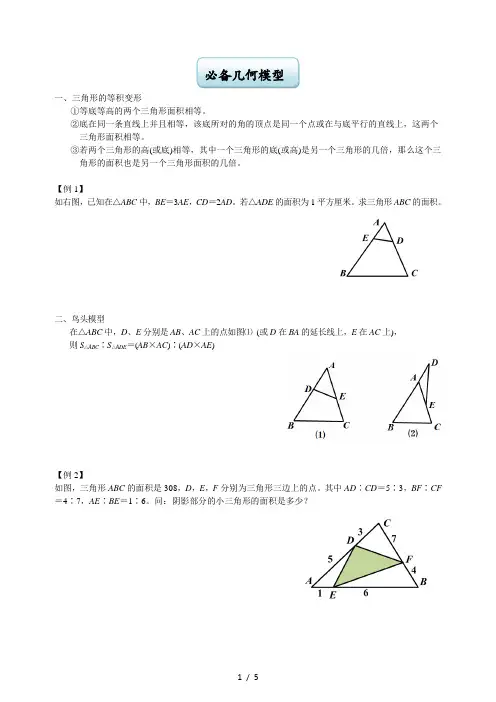
一、三角形的等积变形①等底等高的两个三角形面积相等。

②底在同一条直线上并且相等，该底所对的角的顶点是同一个点或在与底平行的直线上，这两个三角形面积相等。

③若两个三角形的高(或底)相等，其中一个三角形的底(或高)是另一个三角形的几倍，那么这个三角形的面积也是另一个三角形面积的几倍。

【例1】如右图，已知在△ABC中，BE＝3AE，CD＝2AD。

若△ADE的面积为1平方厘米。

求三角形ABC的面积。

二、鸟头模型在△ABC中，D、E分别是AB、AC上的点如图⑴(或D在BA的延长线上，E在AC上)，则S△ABC∶S△ADE＝(AB×AC)∶(AD×AE)【例2】如图，三角形ABC的面积是308，D，E，F分别为三角形三边上的点。

其中AD∶CD＝5∶3，BF∶CF ＝4∶7，AE∶BE＝1∶6。

问：阴影部分的小三角形的面积是多少？必备几何模型【例3】如图，三角形两边上的点都是各边上的五等分点。

问：阴影部分与空白部分的面积比为多少？三、相似三角形性质(沙漏模型)：①AD AE DE AF AB AC BC AG ===②S△ADE∶S△ABC＝AF2∶AG2所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；⑵相似三角形的面积比等于它们相似比的平方；【例4】如图，在平行四边形ABCD中，直线CF交AB于E，交DA延长线于F，若S△ADE＝1，求△BEF的面积。

四、蝴蝶模型任意四边形中的比例关系(“蝴蝶定理”)①S1×S3＝S2×S4②AO∶OC＝(S1＋S2)∶(S4＋S3)①S1∶S3＝a2∶b2②S1∶S2∶S3∶S4＝a2∶ab∶b2∶ab③梯形面积S的对于份数是(a＋b)2【例5】如图面积为12平方厘米的正方形ABCD中，E、F是BC边上的三等分点，求阴影部分的面积。

[转]ppt中全等三角形平移、翻折与旋转动画的制作第一篇：[转]ppt中全等三角形平移、翻折与旋转动画的制作[转] PPT中全等三角形平移、翻折与旋转动画的制作日志[转] PPT中全等三角形平移、翻折与旋转动画的制作2011-7-21 11:39阅读(6)转载自手辰下一篇：PPT中全等三角形...|返回日志列表赞赞赞赞转载(11)分享评论复制地址更多PPT中全等三角形平移、翻折与旋转动画的制作最近帮同事做课件，同事要求实现全等三角形平移、翻折与旋转动画。

平移还容易实现，可翻折和旋转动画以前都是在FLASH中制作。

如何在PPT中实现这两个动画，还真让我费了不少脑筋。

在网上查阅了一下，看到了一个围绕点旋转的动画教程，我试验了一下，旋转动画制作成功。

在此基础上，我进行联想，也实验了翻折的动画。

现整理出来，与大家分享。

1、全等三角形的平移：操作：选定对象/自定义动画/添加效果/动作路径/选择动作方向。

2、全等三角形围绕顶点旋转想让两个全等三角形顶点相连，其中一个三角形绕连接顶点旋转（就像钟表一样）。

绘制一个三角形为A图，复制A，粘贴后生成图B，这时对B进行180度的旋转（注意：建议使用office里默认的旋转工具，让它旋转两次90度，这样可以保证随后点O没有位移）。

在B旋转180度后，移动B图，让其旋转点相接。

这时，选中图A和B，点击右键，“组合”，这时图A和B组合成图C，此时可以将图C中B的颜色及填充色都设定成无，则B看上去就透明不见，但是它实际还是存在的。

图A和图C的顶点对齐，这时再设置图C，设置动画：在组合图形上点击右键，选择“自定义动画”，在“自定义动画”任务窗格中依次点击“添加效果→强调→陀螺旋”，在“数量”一栏改为“半旋转”、“顺时针”即可。

3、全等三角形的翻折想让两个全等三角形底边相连，其中一个三角形绕连接底边翻折（就像翻书一样）。

绘制一个三角形为A图，复制A，粘贴后生成图B，这时对B进行垂直旋转（注意：建议使用office里默认的旋转工具，）。