等积变形(一半模型,三角形等积模型)

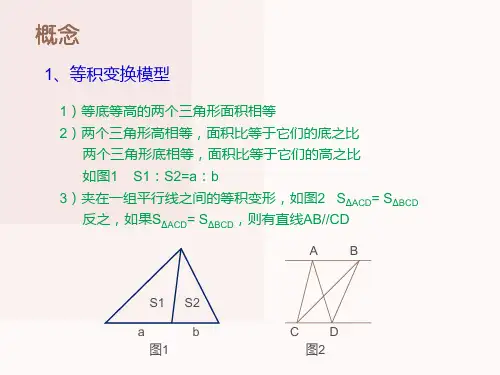
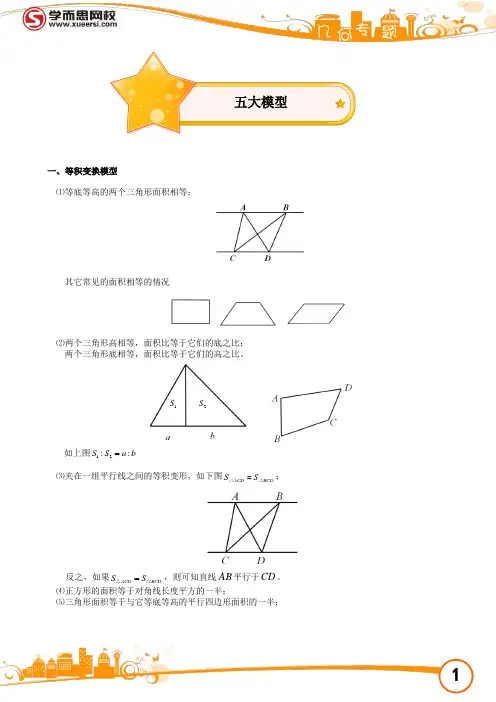
一、等积变换模型⑴等底等高的两个三角形面积相等；其它常见的面积相等的情况⑵两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比。

如上图12::S S a b =⑶夹在一组平行线之间的等积变形，如下图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD 。

⑷正方形的面积等于对角线长度平方的一半；⑸三角形面积等于与它等底等高的平行四边形面积的一半；五大模型1S 2S二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图，在ABC △中，,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上，E 在AC 上(如图2)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。

梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =； ③梯形S 的对应份数为()2a b +。

四、相似模型相似三角形性质：金字塔模型 沙漏模型 ①AD AE DE AFAB AC BC AG===； ②22::ADE ABC S S AF AG =△△。

所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方。

技巧总结1.
牙齿模型2.
平行四边形模型
3.等积变形
思维数学第04讲
一半模型和等积变形（一）
如图，正方形ABCD一半的面积是28平方厘米，矩形DEFG的宽DE＝7厘米，求它的长DG＝?
如图，阴影部分的面积是多少？
如图，已知红色三角形的面积是5，绿色三角形的面积是13，问：三角形OBD的面积是多少？
正方形ABCD和正方形CEFG，且正方形ABCD边长为12厘米，则图中阴影面积为多少平方厘米？
如图，有三个正方形的顶点D、G、K恰好在同一条直线上，其中正方形GFEB 的边长为16厘米，求阴影部分的面积。

课堂中的例题建议重做一遍，再做课后练习，1-3道不会为正常现象。

一个长方形被分成4个不同颜色的三角形，红色三角形的面积是10，黄色三角形的面积是22，绿色三角形的面积是11，那么蓝色三角形的面积是多
少？
如图，正方形ABCD的边长为8，AE＝2，CF＝3。

长方形EFGH的面积为
_______。

如图，长方形ABCD中，AB长18厘米，BC长10厘米，E、F、G、H
分别在长方形的四条边上，其中EC=4厘米，F、G、H均是中点，请问：阴影部分
的面积是多少？
如图，BD长12厘米，DC长4厘米，B、C和D在同一条直线上。

①求三角形ABC的面积是三角形ADC面积的多少倍？
②求三角形ABD的面积是三角形ADC面积的多少倍？
如图所示，ABCD和BEFG是两个正方形，EF长6cm，求阴影部分的面积。

如图所示，大正方形的边长是10cm，求阴影部分的面积。

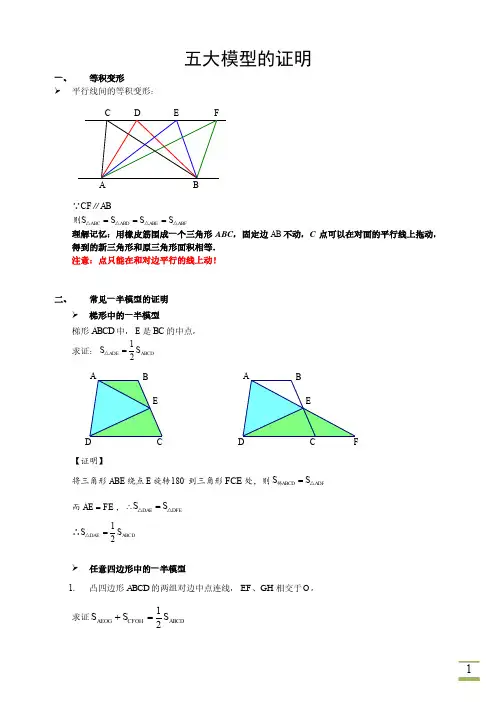
五大模型的证明一、 等积变形平行线间的等积变形：ABC ABD ABE ABFCF ABS S S S ===△△△△∵∥则理解记忆：用橡皮筋围成一个三角形ABC ，固定边AB 不动，C 点可以在对面的平行线上拖动，得到的新三角形和原三角形面积相等． 注意：点只能在和对边平行的线上动！二、常见一半模型的证明 梯形中的一半模型梯形ABCD 中，E 是BC 的中点，求证：12ADE ABCD S S =△【证明】将三角形ABE 绕点E 旋转180到三角形FCE 处，则ADF ABCD S S =△梯 而AE FE =，DAE DFE S S ∴=△△ 12DAE ABCD S S =△∴任意四边形中的一半模型 1.凸四边形ABCD 的两组对边中点连线，EF GH 、相交于O ，求证12AEOG CFOH ABCD S S S +=FEDCBA【证明】连接,,,OA OB OC OD 则()12AEOG AOE AOG AOD AOB S S S S S =+=+△△△△ ()12CFOH COF COH BOC COD S S S S S =+=+△△△△ ()1122AEOG CFOH AOD AOB BOC COD ABCD S S S S S S S +=+++=△△△△∴ 2.顺次连接凸四边形ABCD 四条边的中点E F G H 、、、，求证12EFGH ABCD S S =【证明】连接AC 、FCAFC BFC AF BFS S ==△△∵∴BGF BGFBG CGS S ==△△∵∴14BGF ABC S S =△△∴，同理14DEH ADC S S =△△ 14BGF DEH ABCD S S S +=△△∴，同理14AEF CGH ABCD S S S +=△△∴BAABABFFBA则12EFGH ABCD S S = 三、鸟头模型的证明胖鸟头三角形ABC 中，D 、E 分别是AB 、AC 边上的点， 求证：ADE ABC S AD AES AB AC⨯=⨯△△歪脖鸟头已知三角形ABC ，E 是AC 边上的点，D 在AB 的延长线上，求证：ADE ABC S AD AES AB AC⨯=⨯△△【证明】两种鸟头模型的证明过程相同 连接BECBAABCCBBC12BGF DEH AEF CGH ABCD S S S S S +++=△△△△△∴ADE ABE S ADS AB=△△；ABE ABC S AE S AC =△△ ADE ABE ABE ABC S S AD AES S AB AC ⨯=⨯△△△△ 即ADE ABC S AD AES AB AC=⨯△△旋转型以上两种情况可以通过旋转分别变形成胖鸟头和歪脖鸟头证明． 四、蝴蝶模型的证明任意四边形中的蝴蝶模型（上乘下等于左乘右）【证明】12S COS AO =；34S CO S AO= 则3124S S S S = 所以1423S S S S ⨯=⨯梯形中的蝴蝶模型 1.翅膀相等DBCBAB在梯形ABCD 中，AB DC ∥， 求证：ADO BCO S S =△△【证明】 AB DC ∵∥ABD ABC S S =△△∴ABD ABO ABC ABO S S S S -=-△△△△∴即ADO BCO S S =△△2.梯形中每部分的面积比梯形ABCD 中，AD BC ∥，四个小三角形的面积分别为2134S S S S 、、、，已知AD a =，BC b =，求证各小三角形的面积比【证明】 AD BC ∵∥，AD AO DO a BC CO BO b===∴12S DO aS BO b ==∴，24S AO a S CO b== 则1224S S a aS S b b⨯=⨯∴即2124S a S b =,所以212S a a S b ab==CD综上221234::::::S S S S a ab ab b =五、燕尾模型的证明在三角形ABC 中，E 是BC 上的点，连接AE ，D 是AE 上的点， 求证：ABD ACD S BES CE=△△【证明】ABE ACE S BE S CE =△△，DBE DCE S BES CE =△ ABE DBE ACE DCE S S BES S CE-=-△△△∴即ABD ACD S BES CE=△△。

三角形五大模型【专题知识点概述】本讲复习以前所学过的有关平面几何方面的知识，旨在提高学生对该部分知识的综合运用能力。

重点模型重温一、等积模型①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比；如右图12::S S a b =③夹在一组平行线之间的等积变形，如右图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、等分点结论（“鸟头定理”）DC BAbas 2s 1如图，三角形AED 占三角形ABC 面积的23×14=16三、任意四边形中的比例关系 （“蝴蝶定理”）① S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ② ②AO ︰OC=（S 1+S 2）︰（S 4+S 3）梯形中比例关系（“梯形蝴蝶定理”） ①S 1︰S 3=a 2︰b 2②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; ③S 的对应份数为（a+b ）2模型四：相似三角形性质如何判断相似(1)相似的基本概念：两个三角形对应边城比例，对应角相等。

(2)判断相似的方法：①两个三角形若有两个角对应相等则这两个三角形相似；②两个三角形若有两条边对应成比例，且这两组对应边所夹的角相等则两个S 4S 3s 2s 1O DCBA S 4S 3s 2s 1ba三角形相似。

hh H cb a CB Aac b HC BA①a b c hA B C H=== ; ② S 1︰S 2=a 2︰A 2模型五：燕尾定理S △ABG ：S △AGC ＝S △BGE ：S △GEC ＝BE ：EC ； S △BGA ：S △BGC ＝S △AGF ：S △GFC ＝AF ：FC ； S △AGC ：S △BCG ＝S △ADG ：S △DGB ＝AD ：DB ；【重点难点解析】1. 模型一与其他知识混杂的各种复杂变形2. 在纷繁复杂的图形中如何辨识“鸟头”【竞赛考点挖掘】1. 三角形面积等高成比2. “鸟头定理”3. “蝴蝶定理”F ED CBA【习题精讲】【例1】（难度等级 ※）如图，长方形ABCD 的面积是56平方厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积.【例2】（难度等级 ※）如右图，ABFE 和CDEF 都是矩形，AB 的长是4厘米，BC 的长是3厘米，那么图中阴影部分的面积是____平方厘米．【例3】（难度等级 ※）如图，在三角形ABC 中，BC=8 厘米，AD=6厘米，E 、F 分别为AB 和AC 的中点，那么三角形EBF 的面积是多少平方厘米？【例4】（难度等级 ※※※）如图，在面积为1的三角形ABC 中，DC=3BD,F 是AD 的中点，延长CF 交AB 边于E,求三角GHFED CBA FE DCB AFABCDE形AEF 和三角形CDF 的面积之和。

最全“⼀半”模型结论，掌握这些⾯积计算不再难
⼀半模型是等积变换模型的延伸，但是学⽣往往遇到此类题⽬之后很难想到⽤等积变换的⽅
法，所以专门提炼出⼀半模型，帮助学⽣加深此部分知识点的理解，提⾼⾯积计算的应⽤能
⼒。

长⽅形“⼀半”模型
下图当中阴影均占长⽅形ABCD的⼀半，如果把长⽅形换作平⾏四边形，下⾯结论仍然成⽴，只
是在考察当中多以长⽅形形式出现，如果换作平⾏四边形也要理解。

进⼀步可得如下阴影占长⽅形ABCD⾯积的四分之⼀：
如果把P点移动到下图位置，也就是P点在长⽅形两条长所在直线的外部，那可得阴影⾯积差
（⼤减⼩）占长⽅形ABCD⾯积的⼀半。

三⾓形“⼀半”模型
解释⼀下第⼆⾏第⼀个图形，三⾓形的三条中线在三⾓形内部交于⼀点，该点称作重⼼，三条
中线把三⾓形分成6个⼩三⾓形，这6个⼩三⾓形的⾯积是相等的，因此任取3个三⾓形的⾯积和
占三⾓形ABC⾯积的⼀半。

四边形“⼀半”模型
这三个结论⽐较简单，不⽤过多解释，其中中间的四边形对边中点连线把四边形分成四块，这
四块刚好可以拼成⼀个平⾏四边形。

感兴趣的可以拼⼀下试试。

梯形“⼀半”模型
梯形是四边形，所以四边形具备的⾯积性质梯形也具备，不过梯形的⼀组底边平⾏，还具备以
下性质，其中最后⼀个图形表⽰在两腰中点连线上任意取⼀点，所得图中阴影三⾓形占梯形⾯
积的⼀半，该点只要在腰中点连线上，在梯形外部也成⽴。

特殊“⼀半”模型
下图当中的正⽅形和长⽅形的边是平⾏的。

如果不平⾏则不成⽴。

专题07 三角形中的重要模型-等积模型三角形的面积问题在中考数学几何模块中占据着重要地位，等积变形是中学几何里面一个非常重要的思想，下面的五大模型也都是依托等积变形思想变化而成的，也是学生必须掌握的一块内容。

本专题就三角形中的等积模型（蝴蝶（风筝）模型，燕尾模型，鸟头模型，沙漏模型，金字塔模型）进行梳理及对应试题分析，方便掌握。

模型1. 等积变换基础模型1）等底等高的两个三角形面积相等；如图1，当AB //CD ，则ACD BCD S S =△△； 反之，如果ACD BCD S S =△△，则可知直线AB //CD 。

图1 图2 图32）两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比。

如图2，当点D 是BC 边上的动点时，则S △ABD ∶S △ADC ＝BD ∶DC 。

如图3，当点D 是BC 边上的动点，BE ⊥AD ，CF ⊥AD 时，则S △ABD ∶S △ADC ＝BE ∶CF 。

A ．4B ．3【答案】D 【分析】利用三角形面积公式，等高的三角形的面积比等于底边的比，由此利用已知条件可以分别求出BDC BED S S 、V V ．A．9B．【答案】B【分析】利用中线等分三角形的面积进行求解即可．V【详解】解：∵BD是ABC【答案】12【分析】根据高相等的两个三角形的面积之比等于底之比可得答案．【详解】解：:QCG GF=【答案】14.4【分析】连接BF , 12BDC ABC S S =V V ；根据示为2BDC S V 和3S V∵CD 为AB 边上中线，∵2BE CE =， S \V 2ABC BDC S S \==V V(1)如图2，延长ABC V 的边BC 到点D ，使CD BC =，连接DA （用含a 的代数式表示）；(2)如图3，延长ABC V 的边BC 到点D ，延长边CA 到点E ，使面积为2S ，则2S = （用含a 的代数式表示）；(3)在图3的基础上延长AB 到点F ，使BF AB =，连接FD ，积为3S ，则3S =（用含a 的代数式表示）；Q 延长ABC V 的边BC 到点D ，延长边CA 到点E ，使CD BC =，AE \12ACD AED ECD S S S D D D ==，ACD ABC S D ，22ECD ABC S S a D D \==，即2S （3）由（2）得2ECD ABC S S D D ==同理：22EFA ABC S S a D D ==，2ECD BFD S a D D =，3ECD EFA S S S S D D \=++∵点E 是线段AD 的中点，12BCE ABC S =V ．∥，连接，若过C作CE AB模型2.蝴蝶（风筝）模型蝴蝶模型（定理）提供了解决不规则四边形的面积问题的一个途径。

（一）等高等底◆知识导航◆等高模型△ABC 被AD 分为△ADB 与△ADC,这两个三角形公用高AE，因此称△ADB 与△ADC 共高，因此S △ADB＝BD×AE÷2，S △ADB ＝DC×AE÷2，所以。

当然，△ADB,△ADC 与△ABC 也是共高的，因此，S △ADB :S △ADC :S △ABC ＝BD:DC:BC。

即：高相等，面积之比等于底之比。

◆等底模型△ABC 与△DBC 共用底BC，因此称△ABC 与△DBC 等底，高分别为AE 和DF，因为S△ABC＝BC ×AE÷2,S△DBC＝BC×DF÷2,所以，DFAE DF BC S S DBC ABC =÷⨯÷⨯=∆∆22DF BC 。

即：底相等，面积之比等于高之比。

精准练习1.如图，在△ABC 中，已知三角形DCE 的面积是12，AE:EC=5:2，AD:BD=3:1。

那么△BEC 的面积是多少？2.△ABC 与△DBC 中高AE=10，高DF=4，则两个三角形的面积之比为：_________；若S △ABC =40，则S △DBC =________。

3.△ABC 与△DBC 中高AE＝5，高DF＝6，则这两个三角形的面积之比为：_________；若S △DBC ＝30，则S △ABC ＝_________。

4.已知S △ABC ＝120,S △DBC ＝70，则这两个三角形的高之比为：_______；若AE＝24，则DF＝_________。

5.△ABD 与△ACD 中AD⊥BC，且S △ACD ＝280，S △ABD ＝280,则△ABD 与△ACD 的高之比为：________；若CE＝21，则BE＝_________。

6.△ABD 与△CBD 共用高BE，若AD＝5，CD＝4，则这两个三角形的面积之比为：_________，若S △ABD ＝20，则S △CBD ＝_________。

五大模型的证明一、等积变形平行线间的等积变形：ABC ABD ABE ABFCF ABS S S S △△△△∵∥则理解记忆：用橡皮筋围成一个三角形ABC ，固定边AB 不动，C 点可以在对面的平行线上拖动，得到的新三角形和原三角形面积相等．注意：点只能在和对边平行的线上动！二、常见一半模型的证明梯形中的一半模型梯形ABCD 中，E 是BC 的中点，求证：12ADE ABCDS S △【证明】将三角形ABE 绕点E 旋转180到三角形FCE 处，则ADFABCD S S △梯而AE FE ，DAE DFES S △△12DAE ABCDS S △∴任意四边形中的一半模型1.凸四边形ABCD 的两组对边中点连线，EF GH 、相交于O ，求证12AEOG CFOH ABCDS S S FE D C BA E D CB A A BC D EF【证明】连接,,,OA OB OC OD 则12AEOG AOE AOG AOD AOBS S S S S △△△△12CFOH COF COH BOC CODS S S S S △△△△1122AEOG CFOH AOD AOB BOC COD ABCDS S S S S S S △△△△∴2.顺次连接凸四边形ABCD 四条边的中点E F G H 、、、，求证12EFGH ABCDS S 【证明】连接AC 、FCAFC BFCAF BFS S △△∵∴BGF BGFBG CGS S △△∵∴14BGF ABC S S △△∴，同理14DEH ADCS S △△14BGF DEH ABCD S S S △△∴，同理14AEF CGH ABCDS S S △△∴O H FG E D CB A A BCD E G FH OA B CD E G F H H F G E D CBA则12EFGH ABCDS S 三、鸟头模型的证明胖鸟头三角形ABC 中，D 、E 分别是AB 、AC 边上的点，求证：ADE ABC S AD AES AB AC△△歪脖鸟头已知三角形ABC ，E 是AC 边上的点，D 在AB 的延长线上，求证：ADE ABC S AD AES AB AC△△【证明】两种鸟头模型的证明过程相同连接BEE D C B A AB C DEE D C B A AB CDE12BGF DEH AEF CGH ABCDS S S S S △△△△△∴ADE ABE S AD S AB △△；ABE ABC S AES AC△△ADE ABE ABE ABC S S AD AES S AB AC△△△△即ADE ABC S AD AES AB AC△△旋转型以上两种情况可以通过旋转分别变形成胖鸟头和歪脖鸟头证明．四、蝴蝶模型的证明任意四边形中的蝴蝶模型（上乘下等于左乘右）【证明】12S CO S AO ；34SCOS AO则3124S S S S 所以1423S S S S 梯形中的蝴蝶模型1.翅膀相等E D C B AEDC B As 4s 3s 2s 1O A BCD在梯形ABCD 中，AB DC ∥，求证：ADO BCOS S △△【证明】AB DC∵∥ABD ABCS S △△∴ABD ABO ABC ABOS S S S △△△△∴即ADO BCOS S △△2.梯形中每部分的面积比梯形ABCD 中，AD BC ∥，四个小三角形的面积分别为2134S S S S 、、、，已知AD a ，BC b ，求证各小三角形的面积比【证明】AD BC ∵∥，AD AO DO aBC CO BO b∴12S DO a S BO b ∴，24S AO aS CO b则1224S S a aS S b b∴即2124S a S b ,所以212S a a S b ab A BCD Os 1s 2s 3s 4A B CDO综上221234::::::S S S S a ab ab b 五、燕尾模型的证明在三角形ABC 中，E 是BC 上的点，连接AE ，D 是AE 上的点，求证：ABD ACD S BES CE△△【证明】ABE ACE S BE S CE △△，DBE DCE S BES CE△ABE DBE ACE DCE S S BES S CE△△△∴即ABD ACD S BES CE△△E DCB A。