人教八上11.1-11.3 全等三角形的判定和角平分线的性质精练题易错题

人教版_部编版八年级数学上册第十一章第一节三角形的高、中线与角平分线试题（含答案)已知，如图，OC 是AOB ∠的角平分线，2AOD BOD ∠=∠，18COD ∠=︒.请你求出BOD ∠的度数．【答案】36BOD ∠=︒.【解析】【分析】根据角平分线的定义得到∠BOC=12∠AOB ，根据已知条件得到∠BOD=13∠AOB ；求得∠BOD=2∠COD ，代入数据即可得到结论．【详解】∵OC 是AOB ∠的角平分线 ∴12BOC AOB ∠=∠； ∵2AOD BOD ∠=∠∴3AOB BOD ∠=∠，即13BOD AOB ∠=∠； ∴111236COD AOB AOB AOB ∠=∠-∠=∠ ∴2BOD COD ∠=∠∵18COD ∠=︒∴36BOD ∠=︒.【点睛】本题考查了角平分线的定义，熟记角平分线的定义是解题的关键．72．如图所示，已知∠AOB ＝90°，∠BOC ＝20°，OM 平分∠AOC ，ON 平分∠BOC ；（1）求∠MON ；（2）∠AOB ＝α，∠BOC ＝β，求∠MON 的度数．【答案】（1）45°（2）12α 【解析】【分析】（1）由角平分线的定义及∠MON =∠MOC ﹣∠CON ，可得结论；（2）同理可得：∠MOC 12=（α+β），∠CON 12=β，根据图形便可推出∠MON =∠MOC ﹣∠CON =12α． 【详解】（1）∵OM 平分∠AOC ，ON 平分∠BOC ，∴∠MOC =12∠AOC ，∠NOC =12∠BOC ． ∵∠AOC =∠AOB +∠BOC ，∴∠MON =∠MOC ﹣∠NOC =12（∠AOB +∠BOC ﹣∠BOC ）=12∠AOB ． ∵∠AOB =90°，∴∠MON =12×90°=45°． （2）同理可得：∠MOC =1()2αβ+，∠CON =12β，∴∠MON =∠MOC﹣∠CON =11()22αββ+-=12α． 【点睛】本题考查了角平分线的性质，角的计算，关键在于运用数形结合的思想推出∠AOC =∠AOB +∠BOC ，∠MON =∠MOC ﹣∠CON ．73．如图，O 为直线AB 上一点，OC 为射线，OD 、OE 分别为∠AOC 、∠BOC 的平分线．（1）判断射线OD 、OE 的位置关系，并说明理由；（2）若∠AOD ＝30°，求证：OC 为∠AOE 的平分线；（3）如果∠AOD ：∠AOE ＝2：11，求∠BOE 的度数．【答案】（1）垂直（2）证明见解析（3）70°【解析】【分析】由OD 、OE 分别为∠AOC 、∠BOC 的平分线，可得∠DOE 为180°的一半，可得OD ∠OE ；由OD 为∠AOC 的平分线和∠AOD=30°得到∠COD=∠AOD=30°，由（1）得∠DOE=90°，可得∠COE=60°，又由∠AOC=60°，可得OC 为∠AOE 的平分线；由OD ∠OE 和∠AOD ︰∠AOE=2︰11即可求.【详解】（1）垂直∵OD、OE分别为∠AOC、∠BOC的平分线，∴∠COD=12∠COA ∠COE=12∠COB.∴∠EOD=12∠COA+12∠COB=12∠AOB=90°.∴OD⊥OE.（2）∵∠AOD=30°，∴∠COD=30°.∴∠COE=90-30=60°,∠COA=60°∴∠COE=∠COA.∴OC为∠AOE的平分线.（3）∵∠AOD︰∠AOE=2︰11，∴∠AOD︰∠DOE=2︰9.∴∠AOD=20° .∴∠BOE=90°-20°=70°.【点睛】本题考查的知识点是角平分线定理，解题关键是熟记角平分线定理.74．如图，O为直线AB上一点，OC为一射线，OE平分∠AOC，OF平分∠BOC．求∠EOF的度数.【答案】90°.【解析】【分析】根据角平分线的定义可得∠COE=12∠AOC，∠COF=12∠BOC，然后根据∠EOF=∠COE+∠COF=12(∠AOC+∠BOC)和平角的定义解答．【详解】解：∵O为直线AB上一点∴∠AOB=180°∵OE平分∠AOC，OF平分∠BOC∴∠EOC=12∠AOC，∠COF=12∠BOC∴∠EOF=∠EOC+∠COF=1 2∠AOC+12∠BOC=12(∠AOC+∠BOC)=12∠AOB=12×180°=90°【点睛】本题考查角平分线的定义、平角.75．如图所示，在△ABC中：（1）画出BC边上的高AD；（2）画出中线AE；（3）画出∠B的平分线BF【答案】作图见解析.【解析】【分析】（1）①以A为圆心，AC为半径画弧，交BC延长线于C′，②分别以C、C′为圆心大于1CC′为半径画弧，两弧交于O，③连接AO交BC延长线于D，2BC为半径画弧，则AD即为BC边上的高；（2）①分别以B、C为圆心，大于12两弧交于M、N，②连接MN交BC于E，则AE即为中线，（3）①以B为圆心，PQ 任意长为半径画弧，交AB、BC于Q、P，②分别以P、Q为圆心，大于12为半径画弧，两弧在角内交于F，作射线BF，则BF即为∠ABC的角平分线.【详解】作图如下：【点睛】本题考查了尺规作图：熟悉基本几何图形的基本作图方法是解题关键.76．如图，CB∠OA，∠B＝∠A＝100°，E、F在CB上，且满足∠FOC＝∠AOC，OE平分∠BOF．（1）求∠EOC的度数；（2）若平行移动AC，那么∠OCB：∠OFB的值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；（3）在平行移动AC的过程中，是否存在某种情况，使∠OEB＝∠OCA？若存在，求出∠OCA度数；若不存在，说明理由．【答案】（1）40°；（2）不变，＝1：2；（3）∠OCA＝60°．【解析】【分析】（1）由于BC∥OA，∠B＝100°，易求∠AOB，而OE、OC都是角平分线，从而可求∠COE；（2）利用BC∥OA，可知∠AOC＝∠BCO，又因为∠AOC＝∠COF，所以就有∠FCO＝∠FOC，即∠BFO＝2∠FCO＝2∠OCB，那么∠OCB：∠OFB＝1：2；（3）设∠OCA＝α，∠AOC＝x，根据三角形的外角性质、三角形的内角和定理、平行线的性质可得，α+x＝80°，40°+x＝α，解即可．【详解】解：（1）∠CB∠OA，∠∠BOA+∠B＝180°，∠∠BOA＝80°，∠∠FOC＝∠AOC，OE平分∠BOF，∠∠EOC＝∠EOF+∠FOC＝12∠BOF+12∠FOA＝12（∠BOF+∠FOA）＝12×80°＝40°；（2）不变．∠CB∠OA，∠∠OCB＝∠COA，∠OFB＝∠FOA，∠∠FOC＝∠AOC，∠∠COA＝12∠FOA，即∠OCB：∠OFB＝1：2．（3）在平行移动AC的过程中，存在∠OEB＝∠OCA，且∠OCA＝60°．设∠OCA＝α，∠AOC＝x，∠∠OEB＝∠COE+∠OCB＝40°+x，∠ACO＝80°﹣x，∠α＝80°﹣x，40°+x＝α，∠x＝20°，α＝60°．【点睛】本题考查平移和平行线的性质的有关知识.平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.77．已知：如图，CE是△ABC的一个外角平分线，且EF∥BC交AB于F 点，∠A=60°，∠CEF=55°，求∠EFB的度数．【答案】130°【解析】【分析】根据两直线平行，内错角相等求出∠ECD=∠CEF，再根据角平分线的定义求出∠ACD，然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠B，再根据两直线平行，同旁内角互补求解即可．【详解】∵EF∥BC，∠CEF=55°，∴∠ECD=∠CEF=55°，∵CE是△ABC的一个外角平分线，∴∠ACD=2∠ECD=2×55°=110°，∵∠A=60°，∴∠B=∠ACD-∠A=110°-60°=50°，∵EF∥BC，∴∠EFB=180°-∠B=180°-50°=130°．【点睛】本题考查了平行线的性质，三角形的角平分线的定义，是基础题，熟记性质是解题的关键．78．如图所示，已知直线AB和CD相交于点O，OM平分∠BOD，∠MON ＝90°，∠AOC＝50°．（1）求∠AON的度数．（2）写出∠DON的余角．【答案】（1）65°；（2）∠DOM，∠BOM．【解析】【分析】（1）根据角平分线的定义求出∠MOB的度数，根据邻补角的性质计算即可；（2）根据题意得到，∠DOM为∠DON的余角．【详解】（1）∵∠AOC+∠AOD＝∠AOD+∠BOD＝180°，∴∠BOD＝∠AOC＝50°，∵OM平分∠BOD，∴∠BOM＝∠DOM＝25°，又由∠MON＝90°，∴∠AON＝180°﹣（∠MON+∠BOM）＝180°﹣（90°+25°）＝65°；（2）由∠DON+∠DOM＝∠MON＝90°知∠DOM为∠DON的余角，∵∠AON+∠BOM＝90°，∠DOM＝∠MOB，∴∠AON+∠DOM＝90°，∴∠NOD+∠BOM＝90°，故∠DON的余角为：∠DOM，∠BOM．【点睛】本题考查的是邻补角的概念以及角平分线的定义，掌握邻补角的性质是邻补角互补是解题的关键．79．如图，点A，O，B在同一条直线上，直线CD经过O点，已知∠BOD ＝∠DOE＝∠AOC，OF平分∠AOE，当∠AOC＝28°15′时，求∠EOF的度数．【答案】6145【解析】【分析】依据对顶角相等和邻补角的定义，即可得出∠AOE的度数，再根据角平分线的性质，即可得到∠EOF的度数．【详解】∠∠BOD=∠DOE=∠AOC，∠AOC=28°15′，∠∠AOE=180°-2×（28°15′）=123°30′．又∵OF平分∠AOE，∠∠EOF=1∠AOE=61°45′．2【点睛】本题考查了角平分线的定义，解决问题的关键是利用对顶角相等．80．有这样一个故事，一位老农民的家业是一块任意四边形的土地ABCD，并且在地里有一口井P，井的位置不在地的中间，如图所示，老人想让两个儿子平分他的土地，但井不能分，两家可以共用．老人还没有想出办法，聪明的同学请你帮老人分一下，说明理由．【答案】详见解析.【解析】【分析】取AB，BC，CD，AD的中点F，G，H，E，连接PA，PF，PB，PG，PC，PH，PD，PE．记四边形AFPE的面积为a，四边形BGPF的面积为b，四边形CHPG的面积为c，四边形DEPH的面积为d，则a+c＝b+d．【详解】取AB，BC，CD，AD的中点F，G，H，E，连接PA，PF，PB，PG，PC，PH，PD，PE．记四边形AFPE的面积为a，四边形BGPF的面积为b，四边形CHPG的面积为c，四边形DEPH的面积为d，则a+c＝b+d．理由：∠AF＝FB，BG＝GC，CH＝HD，AE＝ED，∠S△APF＝S△PFB，S△PBG ＝S△PGC，S△PHC＝S△PHD，S△PAE＝S△PDE，∠S△PAF+S△PAE+S△PGC+S△PHC＝S△PFB+S△PBG+S△DEP+S△DHP，∠a+c＝b+d，∴可以把四边形AFPE和四边形CHPG分给一个该儿子，剩下的分给另一个儿子即可．【点睛】本题考查了作图﹣应用与设计，三角形的中线的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考压轴题．。

人教版_部编版八年级数学上册第十一章第一节三角形的高、中线与角平分线试题（含答案)如图，D ，E 分别是△ABC 的边AB ，BC 上的点，AB ＝3BD ，BE ＝CE ．设△ADF 的面积为S 1，△CEF 的面积为S 2，若6ABC S ，则S 1-S 2的值为_____．【答案】1【解析】【分析】根据S △ADF -S △CEF =S △ABE -S △BCD ，所以求出三角形ABE 的面积和三角形BCD 的面积即可，因为AB ＝3BD ，所以AD=2BD ，因为BE=CE ，且S △ABC =6，就可以求出三角形ABE 的面积和三角形BCD 的面积．【详解】解：∵BE=CE ，∴BE=12BC ， ∵S △ABC =6，∴S △ABE =12S △ABC =12×6=3． ∵AB ＝3BD所以AD=2BD ，因为S △ABC =6，∴S △BCD =13S △ABC=13×6=2， ∵S △ABE -S △BCD =（S △ADF +S 四边形BEFD ）-（S △CEF +S 四边形BEFD ）=S △ADF -S △CEF ， 即S △ADF -S △CEF =S △ABE -S △BCD =3-2=1．故答案为：1【点睛】本题主要考查三角形的面积，解决本题的关键知道当高相等时，面积等于底边的比，根据此可求出三角形的面积，然后求出差．62．如图，ABC ∆面积为1，第一次操作：分别延长, , AB BC CA 至点111, , ,A B C 使111, , A B AB B C BC C A CA ===，顺次连结111, , ,A B C ，得到111A B C ∆，第二次操作：分别延长111111,,A B B C C A 至点222,,A B C ，使211121112111, , A B A B B C B C C A C A ===，顺次连结222,,A B C ，得到222A B C ∆， ．．按此规律，要使得到的三角形的面积超过2016，至少经过_________次操作．【答案】4【解析】【分析】先根据已知条件求出△A 1B 1C 1及△A 2B 2C 2的面积，再根据两三角形的倍数关系求解即可．【详解】解：△ABC 与△A 1BB 1底相等（AB=A 1B ），高为1：2（BB 1=2BC ），故面积比为1：2，∵△ABC 面积为1，∴△A 1B 1B 的面积=2．同理可得，△C 1B 1C 的面积=2，△AA 1C 的面积=2，∴△A 1B 1C 1的面积=△C 1B 1C 的面积+△AA 1C 的面积+△A 1B 1B 的面积+△ABC 的面积=2+2+2+1=7；同理可证：△A 2B 2C 2的面积=7△A 1B 1C 1的面积=49，第三次操作后的面积为7×49=343，第四次操作后的面积为7×343=2401．故按此规律，要使得到的三角形的面积超过2016，最少经过4次操作． 故答案为：4．【点睛】本题考查了三角形的面积，此题属规律性题目，解答此题的关键是找出相邻两次操作之间三角形面积的关系，再根据此规律求解即可．63．如图，ABC ∆中，D 、E 、F 、G 分别是边BC 、AC 、DC 、EC 的中点，若22GFC S cm ∆=，则ABC S ∆=__________.【答案】322cm【解析】根据三角形的中点把三角形分成面积相等的两部分进行解答即可．【详解】∵EG ＝CG ，22GFC S cm ∆=，∴△EFC 的面积＝224GFC S cm ∆=，∵DF ＝CF ，24EFC S cm ∆=，∴△ECD 的面积＝228EFC S cm ∆=，∵AE ＝CE ，28ECD S cm ∆=，∴△ACD 的面积＝2216ECD S cm ∆=，∵BD ＝CD ，216ACD S cm ∆=，∴△ABC 的面积＝2232ACD S cm ∆=，故填：322cm .【点睛】此题考查三角形的面积问题，解决本题关键是根据三角形的中点把三角形分成面积相等的两部分求解．64．如图,AM 是ABC 的中线,BMN 的面积为4,BNE 的面积为5,则BCE 的面积____．【答案】13.【解析】根据三角形的中线把三角形分成面积相等的两个三角形可知BMN的面积=的面积4MNC=,即可得出结论.【详解】AM是ABC的中线,BMN=的面积4∴的面积MNC=,BNE的面积为5,=++=．∴的面积44513BCE故答案为：13【点睛】本题考查三角形的面积问题，熟练掌握三角形的中线把三角形分成面积相等的两个三角形是解题关键.65．如图，AD是△ABC的中线，若AB：AC＝3：4，则S△ABD：S△ACD ＝_____．【答案】1：1．【解析】【分析】根据中线的定义得到DB=CD，然后根据等底等高的三角形的面积相等即可得到S△ABD=S△ACD．解：在△ABC中，∵AD是△ABC的中线，∴BD=CD，=S△ACD，∴S△ABD：S△ACD=1：1．∴S△ABD故答案为：1：1．【点睛】本题考查三角形中线的定义与性质，熟练掌握中线的性质是解题关键．66．已知三角形的两边的长分别为2cm和8cm，设第三边中线的长为x cm，则x的取值范围是_______【答案】3＜x＜5【解析】【分析】延长AD至M使DM=AD，连接CM，先说明△ABD≌△CDM，得到CM=AB=8，再求出2AD的范围，最后求出AD的范围.【详解】解：如图：AB=8，AC=2，延长AD至M使DM=AD，连接CM在△ABD 和△CDM 中，AD MD ADB MDC BD CD =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△MCD （SAS ），∴CM=AB=8．在△ACM 中：8-2＜2x ＜8+2，解得：3＜x ＜5．故答案为：3＜x ＜5．【点睛】本题考查了三角形的三边关系，解答的关键在于画出图形，数形结合完成解答.67．如图，点O 是三角形内角平分线的交点，点I 是三角形外角平分线的交点，则∠O 与∠I 的数量关系是_____________【答案】∠O +∠I =180°【解析】【分析】根据交平分线性质，可推出∠OBI=∠OCI=90°，然后在四边形OBIC 中，利用内角和可得出∠O 与∠I 的数量关系.【详解】∵BO 平分∠ABC ，∴∠OBC=1ABC 2∠， ∵BI 平分∠CBD ，∴∠CBI=1CBD 2∠ ∴()1OBC+CBI=ABC+CBD =902∠∠∠∠ 即∠OBI=90°同理可得∠OCI=90°，在四边形OBIC 中，O+I+OBI+OCI=360∠∠∠∠∴∠O +∠I =180°【点睛】本题考查角平分线和四边形内角和，熟练掌握内角和是解题的关键.68．如图所示，,,BDE DEC ACE ∆∆∆的面积相等，ADE ∆的面积为1，则ABC ∆的面积是______．【答案】6【解析】【分析】根据,,BDE DEC ACE ∆∆∆的面积相等得出△BED 和△AEC 的关系以及D 是BC 中点，从而得出△ABD 的面积，根据△ABD 和△ACD 的面积相等得出△ABC 的面积.【详解】解: ,,BDE DEC ACE ∆∆∆的面积相等，∴△BEC 的面积是△AEC 面积的2倍，D 为BC 中点，∴S △ABD =S △ACD ，∵△BEC 和△AEC 高相等，∴BE=2AE ，∵ADE ∆的面积为1，∴S △BED =2S △AED =2，∴S △ABD =3，∴S △ABC =6.【点睛】本题考查了三角形面积的计算；熟记三角形面积公式，找出三角形的面积关系是解决问题的关键．69．如图，已知点O 是ABC ∆的重心，那么:BOC ABC S S ∆∆=__．【答案】1:3【解析】【分析】延长BO交AC于D，由重心的性质可得AD=DC，BO=2OD，再根据三角形的面积公式进行计算即可．【详解】如图所示：延长BO交AC于D，设点E是BC上的中点，连接AE，过点E 作EF//BD交AC于点F，∵点O是ABC∆的重心，AD DC∴=，BE＝EC，又∵BD//EF,BE=CD,∴DF＝12DC=FC，又∵AD＝DC，∴DF＝12 AD，又∵OD//EF,∴OD:EF=AD:AF=1:3 2 ,又∵EF＝12BD，∴OD：12BD＝1：32，即OD：BD＝1：3，∴2BO OD=，又∵AD ＝DC ，12ADB BDC ABC S S S ∆∆∆∴==，2BOC ODC S S ∆∆=， 23BOC BDC S S ∆∆∴=， :1:3BOC ABC S S ∆∆∴=，故答案是：1:3．【点睛】考查的是三角形的重心的概念和性质，解题关键是利用了三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．70．如图，ABC ∆中，G 为重心，2BGC S ∆=，那么ABC S ∆=______________；【答案】6【解析】【分析】根据重心到顶点的距离是它到对边中点的距离的2倍和已知可以求出△ABC 的面积．【详解】解：如图示，连接AG 交BC 于D 点，作△ABC 的高h 1，做△BCG 的高h 2，∵G 为△ABC 的重心，根据重心到顶点的距离是它到对边中点的距离的2倍，∴AD=3GD ，∴123h h =，∵2BGC S =， ∴2111113336222ABC BCG S BC h BC h BC h S ===⨯==，【点睛】本题考查的是三角形的重心的知识，掌握重心到顶点的距离是它到对边中点的距离的2倍是解题的关键．。

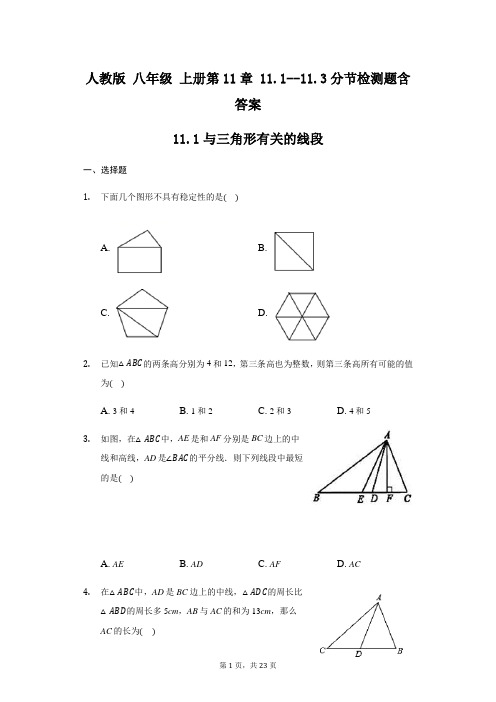
人教版八年级上册第11章 11.1--11.3分节检测题含答案11.1与三角形有关的线段一、选择题1.下面几个图形不具有稳定性的是()A. B.C. D.2.已知△ABC的两条高分别为4和12，第三条高也为整数，则第三条高所有可能的值为()A. 3和4B. 1和2C. 2和3D. 4和53.如图，在△ABC中，AE是和AF分别是BC边上的中线和高线，AD是∠BAC的平分线．则下列线段中最短的是()A. AEB. ADC. AFD. AC4.在△ABC中，AD是BC边上的中线，△ADC的周长比△ABD的周长多5cm，AB与AC的和为13cm，那么AC的长为()A. 7cmB. 8cmC. 9cmD. 10cm5.如图，在△ABC中，E是边BC的任意一点，AD垂直BC于点D，则以AD为高的三角形有()．A. 3个B. 4个C. 5个D. 6个6.下列图形中具有稳定性的是()A. 平行四边形B. 等腰三角形C. 长方形D. 梯形7.如图，在△ABC中，AD，AE，AF分别是三角形的高线，角平分线及中线，那么下列结论错误的是()．A. AD⊥BCB. BF=CFC. BE=ECD. ∠BAE=∠CAE8.下面是一位同学用三根木棒拼成的图形，其中符合三角形概念的是()．A. B. C. D.9.如图，∠1=∠2，∠3=∠4，下列结论中错误的是()．A. BD是△ABC的角平分线B. CE是△BCD的角平分线∠ACBC. ∠3=12D. CE是△ABC的角平分线10.长为9，6，5，4的四根木条，选其中三根组成三角形，选法有()A. 1种B. 2种C. 3种D. 4种11.若一个三角形的两边长分别为2和4，则该三角形的周长可能是()A. 6B. 7C. 11D. 12二、填空题12.若a，b，c为△ABC的三边长，且满足|a−4|+√b−2=0，则c的值可以为_________．13.如图，在△ABC中，AC=8，BC=6，AD⊥BC于D，AD=5，BE⊥AC于E，则BE的长为_________．14.如图，在△ACB中，∠ACB=90°，CD⊥AB，则以∠A为内角的三角形是__________，以BC为边的三角形是___________，∠B所对的边为___________．15.有四条线段，长分别为3cm、5cm、7cm、9cm，如果用这些线段组成三角形，可以组成______ 个三角形．16.如图，D，E分别是△ABC的边AB，AC的中点，若△ADE的面积为1，则四边形DBCE的面积等于______．三、解答题17.如图，AD是△ABC的边BC的中线，已知AB=5cm，AC=3cm，求△ABD与△ACD的周长之差．18.如图，回答下列问题：(1)图中有________个三角形，它们分别是______________________；(2)以线段AD为边的三角形是__________________；(3)线段CE所在的三角形是________，CE边所对的角是________．19.已知AD是△ABC的高，∠BAD=70°，∠CAD=20°，求∠BAC的度数．答案和解析1.A解：根据三角形的稳定性可得，B、C、D都具有稳定性．不具有稳定性的是A选项．故选A．2.D解：设边长为a，b的边上的高分别为4，12，边长为c的边上的高为h，△ABC的面积是S，那么a=2S4，b=2S12，c=2Sℎ．∵a−b<c<a+b．∴2S4−2S12<c<2S4+2S12，即S3<2Sℎ<2S3，解得3<ℎ<6．∴ℎ=4或5．3.C解：∵在△ABC中，AF是高，∴AF⊥BC，又∵在△ABC中，AD是∠BAC的平分线，AE是BC边上的中线，∴AF<AD，AF<AE，AF<AC，故最短线段为AF．4.C解∵AD是BC边上的中线，所以D为BC的中点CD=BD，∵△ADC的周长比△ABD的周长多5cm，AD=AD，∴AC−AB=5cm，又∵AB+AC=13cm，∴AC=9cm即AC的长度是9cm．5.D解：AD垂直BC于点D，则以AD为高的三角形有△ABD，△AED，△ABE，△ADC，△ABC，△AEC，共6个．故选D．6.B解：根据三角形具有稳定性，可知四个选项中只有等腰三角形具有稳定性的．．7.C解：根据△ABC中，AD，AE，AF分别是三角形的高线，角平分线及中线，可得AD⊥BC，∠BAE=∠CAE，BF=CF，不能得到BE=EC．8.D解：因为三角形是由不在同一条直线上的三条线段首尾顺次相接所成的图形．所以D 符合题意．9.D解：由∠1=∠2，∠3=∠4，根据角平分线的性质，可知：BD是△ABC的角平分线，故A正确；CE是△BCD的角平分线，故B正确；∠ACB，故C正确；∠3=12CE是△ABC的角平分线是错误的，三角形的角平分线是角的顶点与对边交点之间的线段，故D错误．10.C解：四根木条的所有组合：9，6，5和9，6，4和9，5，4和6，5，4；根据三角形的三边关系，得能组成三角形的有9，6，5和9，6，4和6，5，4．11.C解：设第三边的长为x，∵三角形两边的长分别是2和4，∴4−2<x<2+4，即2<x<6．则三角形的周长：8<C<12，C选项的11符合题意，12.3(答案不唯一)解：∵|a−4|+√b−2=0，∴a−4=0，a=4；b−2=0，b=2；则4−2<c<4+2，2<c<6，3符合条件．故答案为3(答案不唯一) 13.154解：∵SΔABC=12AC·BE，SΔABC=12BC·AD，∴AC·BE=BC·AD，∵AC=8cm，BC=6cm，AD=5cm，∴BE=BC·ADAC =6×58=154(cm)。

人教版_部编版八年级数学上册第十一章第一节三角形的高、中线与角平分线试题（含答案)如图，AD是△ABC的高，AE是△ABC的角平分线，AF是△ABC的中线，图中相等的角有________________________________，相等的线段有__________.【答案】∠BAE＝∠CAE，∠ADB＝∠ADC BF＝CF【解析】【分析】根据相关定义可知：三角形角平分线可以得到相关角相等；中线可以得出相关线段相等；高也可以得出相关角相等.【详解】因为AD是△ABC的高，所以△ADB＝△ADC=90o;因为AE是△ABC的角平分线，所以△BAE＝△CAE；因为AF是△ABC的中线，所以BF=CF.所以相等的角有：△BAE＝△CAE，△ADB＝△ADC；相等的线段有BF＝CF.故答案为△BAE＝△CAE，△ADB＝△ADC；BF＝CF.【点睛】本题主要考查三角形的高线、角平分线、中线的定义. 只要熟练掌握和理解三角形的高线、中线和角平分线的定义即可顺利解决此类问题.72．从三角形的一个顶点向它的对边所在的直线作____，顶点和____之间的线段叫做三角形的高线，简称三角形的高．三角形三条高所在的直线______，这点叫做三角形的垂心．【答案】垂线垂足相交于一点【解析】【分析】直接根据教材对三角形高线的描述即可得出答案.【详解】根据教材描述：“从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高线，简称三角形的高．三角形三条高所在的直线相交于一点，这点叫做三角形的垂心．”可填空.故答案为：(1)垂线；(2)垂足；(3)相交于一点.【点睛】本题考核知识点：三角形的高线. 解题关键点：熟记教材中对三角形高线概念的相关描述.73．在三角形中，一个内角的______与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线．三角形的三条角平分线________________.【答案】平分线相交于一点【解析】【分析】根据教材对三角形角平分线的描述即可得出答案.【详解】根据教材：“在三角形中，一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线．三角形的三条角平分线相交于一点.”可得答案.故答案为：(1)平分线;(2)相交于一点.【点睛】本题考核知识点：三角形角平分线. 解题关键点：熟记教材中对三角形角平分线的概念描述.74．如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8，四边形DHOG面积为（）A．6 B．7 C．8 D．9【答案】B【解析】连接OC，OB，OA，OD，△E、F、G、H依次是各边中点，△△AOE和△BOE等底等高，所以S△OAE=S△OBE，同理可证，S△OBF=S△OCF，S△ODG=S△OCG，S△ODH=S△OAH，△S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE，△S四边形AEOH=6，S四边形BFOE=7，S四边形CGOF=8，△6+8=7+S四边形DHOG，解得S四边形DHOG=7．故答案为7．点睛：本题考查了三角形的面积.解决本题的关键将各个四边形划分,充分利用给出的中点这个条件,证得三角形的面积相等,进而证得结论.75．如图，AE是△ABC的角平分线，AD⊥BC于点D，若∠BAC=130°，⊥C=30°，则∠DAE的度数是__________.【答案】5°【分析】根据直角三角形两锐角互余求出∠CAD ，再根据角平分线定义求出∠CAE ，然后根据∠DAE=∠CAE-∠CAD ，代入数据进行计算即可得解．【详解】△AD △BC ，△C=30°，△△CAD=90°-30°=60°，∵AE 是△ABC 的角平分线，∠BAC=130°，△△CAE=12△BAC=12×130°=65°， △△DAE=△CAE-△CAD=65°-60°=5°．故答案为：5°．【点睛】本题考查了三角形的内角和定理，三角形的角平分线，高线的定义，准确识图，找出各角度之间的关系并求出度数是解题的关键．76．如图，D 、E 分别是ABC 边AB ，BC 上的点，AD =2BD ，BE =CE ，设ADF 的面积为1S CEF △ 的面积为2S ，若6ABC S =，则12S S -的值为____________.【答案】1；【解析】S△ADF−S△CEF＝S△ABE−S△BCD，所以求出三角形ABE的面积和三角形BCD的面积即可，因为AD＝2BD，BE＝CE，且S△ABC＝6，就可以求出三角形ABE 的面积和三角形BCD的面积.【详解】解：∵BE＝CE，∴BE＝12 BC，∵S△ABC＝6，∴S△ABE＝12S△ABC＝12×6＝3．∵AD＝2BD，S△ABC＝6，∴S△BCD＝13S△ABC＝13×6＝2，∵S△ABE−S△BCD＝（S1＋S四边形BEFD）−（S2＋S四边形BEFD）＝S1−S2＝3-2=1，故答案为1【点睛】本题考查三角形的面积，关键知道当高相等时，面积等于底边的比，据此可求出三角形的面积，然后求出差．77．如图，分别是线段的中点，若的面积是1，那么的面积是______【答案】7【解析】试题分析：如图，连接AB1，BC1，CA1，∵A、B分别是线段A1B，B1C的中点，∴S△ABB1＝S△ABC＝1，S△A1AB1＝S△ABB1＝1，∴S△A1BB1＝S△A1AB1＋S△ABB1＝1＋1＝2，同理：S△B1CC1＝2，S△A1AC1＝2，∴△A1B1C1的面积＝S△A1BB1＋S△B1CC1＋S△A1AC1＋S△ABC＝2＋2＋2＋1＝7．故答案为：7．点睛：本题考查了三角形中线的性质，熟记三角形的中线可将三角形分成面积相等的两部分是解题的关键．78．已知△ABC中，AE为BC边上的高线，若∠ABC=50°，∠CAE=20°，则∠ACB=_____°．【答案】70或110．【解析】∵AE⊥BC，∴∠BAE+∠ABC=90°，∴∠BAE=90°﹣50°=40°，分两种情况：①当∠ACB为锐角时，如图1，在△AEC中，∠ACB+∠CAE=90°，∴∠ACB=90°﹣20°=70°，②当∠ACB为钝角时，如图2，则∠ACB=∠CAE+∠AEC=20°+90°=110°，故答案为：70或110．79．如图，在△ABC 中，AD 为BC 边上的中线，DE⊥AB 于点E，DF⊥AC 于点F，AB=3，AC＝4，DF＝1.5，则DE=_______．【答案】2【解析】【分析】由题意，△ABC 中，AD 为中线，可知△ABD 和△ADC 的面积相等；利用面积相等，问题可求．【详解】∵△ABC 中，AD 为中线，∴BD =DC ,∴,ABD ADC S S =∵DE ⊥AB 于E ，DF ⊥AC 于F ，AB =3，AC =4，DF =1.5， ∴1122AB ED AC DF ⋅⋅=⋅⋅， ∴1134 1.522ED ⨯⨯=⨯⨯， ∴DE =2.故答案为2.【点睛】考查三角形中线的性质以及三角形的面积公式，掌握三角形的中线可以把三角形的面积等分是解题的关键.80．如图，在△ABC 中，D 、E 分别是BC 、AD 的中点，S △ABC =12cm 2，那么S △ABE 为____cm 2.【答案】3【解析】△D是BC的中点，△S△ABD=12S△ABC=12×12=6cm2，△E是AD的中点，△S△ABE=12S△ABD=12×6=3cm2．故答案为3．点睛: 本题考查了三角形的面积，根据等底等高的三角形的面积相等，理解三角形的中线把三角形分成两个面积相等的三角形是解题的关键．。

人教版数学八年级上册第□章1112三角形的高、中线与角平分线同步练习一、单选题（共10题；共20分）1、如图，AABC 中，ZACB=90°, CD±AB, ZA=30°,那么 S AAB c ： S ABCD =（）B 、$ 1C 、 3： 1D 、 4： 12、在坐标系中，己知A （2, 0） , B （ - 3, -4） , C （0, 0）,则AABC 的面积为（） A 、 4 B 、 6 C 、 8 D 、 3A 、3个B 、 4个C 、 5个D 、6个3、如图，在方格纸屮每个小方格都是边长为1的正方形，A 、B 两点在小方格的顶点上,的顶点上，且以A 、B 、C 为顶点的三角形的面积为1个平方单位，则点C 的个数为（ArB点C 也在小方格那么（）A 、2： 14、如图，AD和BE是AABC的两条屮线，设AABD的面积为®, ABCE的面积为S?A、S i>S2B、S i=S2C、Si<S2D、不能确定B、23C、24D、256、已知SAABC=4cm2 ,点E为BC中点，点D为BE中点，则S AABD=（）cm2•A、2B、3C、1Ds 1.57＞如图,AD是Z\ABC的边BC上的中线,DE=2AE,且S AABC=24,则S^BE为（）Ax 4B、6C、88、如图为等边AABC与正方形DEFG的重叠情形，其中D. E两点分别在AB. BC上，且BD=BE,若AB=3,DE=1,则Z\EFC的面积为（）A、B、19、 下列说法正确的是（） A 、 三角形的三条高都在三角形的内部 B 、 等边三角形--角的平分线是一条射线 C 、 三个角对应相等的三角形全等D 、 两直角边对应相等的两个直角三角形全等10、 下列叙述中：①任意一个三角形的三条高至少有一条在此三角形内部；② 以a, b, c 为边（a, b, c 都大于0,且a+b>c ）可以构成一个三角形； ③ 一个三角形内角之比为3： 2： 1,此三角形为直角三角形； ④ 有两个角和一条边对应相等的两个三角形全等； 正确的有（）个.A 、 1B 、 2C 、 3D 、 4二、填空题（共5题；共7分）11、 己知三角形的三边长分别为5, 5, 6,则该三角形的面积为 _____________ .12、 如果点A （0, 1） , B （3, 1）,点C 在y 轴上，且AABC 的面积是3,则C 点坐标 _________________ ・13、 如图，过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ,那么图中矩形AMKP14、 在平面直角坐标系xOy 中，直线y= 与x 轴的交点坐标为 _________ ,与y 轴的交点坐标为________ ,与坐标轴所围成的三角形的面积等于 __________ •15、 如图，在矩形 ABCD 中，点 E 、F 分别在 AB 、DC 上，BF/7DE,若 AD=12cm, AB=7cm,且 AE ： EB=5：2,则阴影部分的面积为 _________c、D、的面积Si 与矩形QCNK 的面积S 2的大小关系是 _________（填'或"V"或"=〃）三、计算题（共1题；共5分）度数.四、解答题（共1题；共5分）17、求图中四边形ABCD的面积.五、综合题（共1题；共10分）18、如图，在Z\ABC 屮，ZB=40°, ZC=60°, AD 丄BC 于D, AE 是ZB AC 的平分⑴求ZDAE的度数；⑵写出以AD为高的所有三角形.答案解析部分一、单选题1、【答案】D【考点】三角形的面积，含30度角的直角三角形【解析】【解答】解：・・・ZACB=90。

人教版_部编版八年级数学上册第十一章第一节三角形的高、中线与角平分线试题（含答案)一、单选题1．对于任意三角形的高，下列说法不正确的是（）A．锐角三角形有三条高B．直角三角形只有一条高C．任意三角形都有三条高D．钝角三角形有两条高在三角形的外部【答案】B【解析】【分析】【详解】试题分析：直角三角形有3条高，其中有两条就是直角三角形的两条直角边．考点：三角形的三线2．如图，三角形ABC中，D为BC上的一点，且S△ABD=S△ADC，则AD 为（）A．高B．角平分线C．中线D．不能确定【答案】C【解析】试题分析：三角形ABD和三角形ACD共用一条高，再根据S△ABD=S△ADC，列出面积公式，可得出BD=CD．解：设BC边上的高为h，∵S△ABD=S△ADC，∵，故BD=CD，即AD是中线．故选C．考点：三角形的面积；三角形的角平分线、中线和高．3．三角形三条中线的交点叫做三角形的A．内心B．外心C．中心D．重心【答案】D【解析】试题分析：三角形的重心是三角形三条中线的交点．故选D．考点：三角形的重心．4．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B． C．D．【答案】A【解析】【分析】经过一个顶点作对边所在的直线的垂线段，叫做三角形的高，根据概念即可得出.【详解】根据定义可得A是作BC边上的高，C是作AB边上的高，D是作AC边上的高.故选A.考点：三角形高线的作法5．下列四个图形中，线段BE是△ABC的高的是（）A．B．C．D．【答案】D【解析】试题分析：根据三角形的高线的定义可得，则D选项中线段BE是∵ABC的高.考点：三角形的高6．如图，CD，CE，CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是（）A．AB＝2BF B．∠ACE＝1∠ACB2C．AE＝BE D．CD⊥BE【答案】C【解析】【分析】【详解】试题分析:∵CD，CE，CF分别是∵ABC的高、角平分线、中线∵ACB ，AB=2BF∵CD∵BE，∵ACE=12故选B考点：三角形的高，角平分线，中线..7．下列命题中，正确的是（）A．三角形的一个外角大于任何一个内角B．三角形的一条中线将三角形分成两个面积相等的三角形C．两边和其中一边的对角分别相等的两个三角形全等D．三角形的三条高都在三角形内部【答案】B【解析】试题分析：A、当钝角三角形时，钝角的外角就小于内角；C、当两条边和两边的夹角对应相等的时候，两个三角形全等；D、当三角形为直角三角形时，其中有两条高在三角形上.考点：三角形的性质.8．如图，△ABC 中，AD 为△ABC 的角平分线，BE 为△ABC 的高，∠C=70°，∠ABC=48°，那么∠3是（ ）A ．59°B ．60°C ．56°D ．22°【答案】A【解析】【分析】【详解】 根据题意可得，在∵ABC 中，70,48︒︒∠=∠=C ABC ，则62︒∠=CAB ，又AD 为∵ABC 的角平分线，1262231︒︒∴∠=∠=÷=又在∵AEF 中，BE 为∵ABC 的高∴90159359︒︒︒∠=-∠=∴∠=∠=EFA EFA考点：1、三角形的内角内角之和的关系 2、对顶角相等的性质.9．下列说法错误的是（ ）．A ．锐角三角形的三条高线，三条中线，三条角平分线分别交于一点B ．钝角三角形有两条高线在三角形外部C ．直角三角形只有一条高线D ．任意三角形都有三条高线，三条中线，三条角平分线【答案】C【解析】试题分析：A、正确，锐角三角形的三条高线、三条中线、三条角平分线分别交于一点；B、正确，钝角三角形有两条高线在三角形的外部；C、错误，直角三角形也有三条高线；D、正确．故选C．考点：三角形的角平分线、中线和高．10．如图所示，AM是△ABC的中线，那么若用S1表示△ABM的面积，用S2表示△ACM的面积，则S1和S2的大小关系是( )A．S1＞S2B．S1＜S2C．S1=S2D．以上三种情况都有可能【答案】C【解析】试题分析:由图可得，AM是∵ABC的中线，显然，∵ABM与∵ACM有长度相等的边，即BM=CM，又这两边上的高相等，即∵ABC中BC边上的高，所以，S1=S2.故选C.考点：三角形的中线.。

人教版_部编版八年级数学上册第十一章第一节三角形的高、中线与角平分线试题（含答案)一、单选题1．如图，在△ABC中，点F，D，E分别是边AB，BC，AC上的点，且AD，BE，CF相交于点O，若点O是△ABC的重心，则以下结论：①线段AD，BE，CF是△ABC的三条角平分线；②△ABD的面积是△ABC面积的一半；③图中与△ABD面积相等的三角形有5个；④△BOD的面积是△ABD面积的13；⑤AO ＝2OD其中一定正确结论有（）A．①③④⑤B．②③④⑤C．③④⑤D．①②③④【答案】B【解析】【分析】根据三角形重心的概念和性质即可判定．【详解】∵点O是△ABC的重心，∴线段AD，BE，CF是△ABC的三条中线，故①错误；∵AD是中线，∴BD＝12 BC，∴△ABD的面积是△ABC面积的一半；故②正确；∵AD，BE，CF是△ABC的三条中线，∴△ABD面积＝△ACD面积＝12△ABC面积，△ABE面积＝△CBE面积＝12△ABC面积，△ACF面积＝△BCF面积＝12△ABC面积，∴△ABD面积＝△ACD面积＝△ABE面积＝△CBE面积＝△ACF面积＝△BCF面积，∴图中与△ABD面积相等的三角形有5个，故③正确；∵点O是△ABC的重心，∴OA＝2OD，∴OD＝13 AD，∴△BOD的面积是△ABD面积的13；故④⑤正确；综上，②③④⑤，故选：B．【点睛】本题考查三角形重心的概念和性质，三角形的重心是三角形三条中线的交点，性质如下：1.重心到顶点的距离与重心到对边中点的距离之比为2：1；2.重心和三角形3个顶点组成的3个三角形面积相等；3.重心到三角形3个顶点距离的平方和最小；4. 重心和三角形3个顶点的连线的任意一条连线将三角形面积平分；5. 重心是三角形内到三边距离之积最大的点.2．如图，在ABC中，ABD ACDS S，AB比AC长4，ABD△的周长为21，则ACD 的周长为（ ）A ．16B ．17C ．19D ．25【答案】B【解析】【分析】 根据三角形中线的定义可得BD ＝CD ，再表示出△ABD 和△ACD 的周长的差就是AB 、AC 的差，然后计算即可．【详解】∵ABD ACD S S∴AD 是BC 边上的中线，∴BD ＝CD ，∴△ABD 和△ACD 周长的差＝（AB ＋BD ＋AD ）−（AC ＋AD ＋CD ）＝AB −AC ，∵△ABD 的周长为21，AB 比AC 长4，∴△ACD 周长为：21−4＝17故选：B ．【点睛】本题主要考查了三角形的中线的定义，把三角形的周长的差转化为已知两边AB 、AC 的长度的差是解题的关键．3．如图，若ABC ∆的三条角平分线AD 、BE 、CF 交于点G ，则与EGC ∠互余的角是( )A ．CGD ∠B ．FAG ∠C ．ECG ∠D ．FBG ∠【答案】B【解析】【分析】 根据三角形角平分线的定义、互余的定义和垂直的定义逐一判断即可．【详解】解：∵三角形的两个角平分线不一定互相垂直，∴∠EGD 不一定等于90°∴EGC ∠与CGD ∠不一定互余，故A 选项不符合题意；∵∠BAC ＋∠ABC ＋∠ACB=180°，ABC ∆的三条角平分线AD 、BE 、CF 交于点G∴∠FAG=12∠BAC ，∠GBC=12∠ABC ，∠GCB=12∠ACB ∴∠FAG ＋∠GBC ＋∠GCB=12（∠BAC ＋∠ABC ＋∠ACB ）=90° ∵EGC ∠=∠GBC ＋∠GCB∴EGC ∠＋∠FAG=90°，故B 选项符合题意；∵三角形一个内角的角平分线不一定垂直该角的对边∴∠GEC 和∠GFB 不一定是直角∴EGC ∠＋∠ECG 不一定等于90°，故C 选项不符合题意；∠FGB ＋∠FBG 不一定等于90°∵∠FGB=EGC ∠∴EGC ∠＋∠FBG 不一定等于90°，故D 选项不符合题意．故选B ．【点睛】此题考查的是互余的判定，掌握角平分线的定义、互余的定义和垂直的定义是解决此题的关键．4．如图，点D 和点E 分别为ABC ∆中AB 、AC 的中点，212ABC S cm ∆=，则ADE S ∆=（ ）A ．22cmB ．23cmC ．24cmD ．26cm【答案】B【解析】【分析】 根据三角形中线等分三角形的面积即可求解．【详解】∵点D 为ABC 中AB 的中点， ∴1112622ADC ABC S S ==⨯=(2cm )， ∵点E 分别为ADC 中AC 的中点，∴116322ADE ADCS S==⨯=(2cm) ．故选：B．【点睛】本题主要考查三角形中线性质的理解，三角形中线能将三角形分成面积相等的两部分的应用是解题的关键．5．在平面直角坐标系中，一个智能机游人接到如下指令：从原点O出发，按回右，向上，向右，向下的方向依次不断移动，每次移动1m．其行走路线如图所示，第1次移动到A1，第2次移动到A2，…，第n次移动到A n，则△OA2A2019的面积是( )A．504m2B．10092m2C．10112m2D．1009m2【答案】B【解析】【分析】根据题意求出A2A2019的长度，再根据三角形的面积公式求出△OA2A2019的面积即可．【详解】由题意知OA4n=2n．∵2018÷4=504…2，∴A2A201920162=+1=1009，∵A2A2019∥x轴，∴△OA2A2019的面积是12⨯1×100910092=(m2)．故选：B．【点睛】本题考查了三角形的面积问题，掌握三角形的面积公式是解题的关键．6．对三角形的高、中线和角平分线概念理解错误．．的是（）A．直角三角形只有一条高B．钝角三角形有两条高在三角形外部C．锐角三角形的三条高、三条中线、三条角平分线分别交于一点D．任意三角形都有三条高、三条中线、三条角平分线【答案】A【解析】【分析】根据三角形的高线、中线、角平分线的性质逐一分析各个选项即可．【详解】解：A、错误，直角三角形也有三条高线；B、正确，钝角三角形有两条高线在三角形的外部；C、正确，任意三角形的三条高线、三条中线、三条角平分线分别交于一点；D、正确．故选：A．【点睛】本题考查了三角形的高线、中线、角平分线的性质．熟练掌握三角形的高线、中线、角平分线的性质是解题的关键.7．如图所示,在△ABC中，已知点D为边BC 的中点，且S△ABC=4cm2,则S△ADC等于（）A．2cm2B．1cm2C．x cm2D．x cm2【答案】A【解析】【分析】根据三角形的中线把三角形分成面积相同的两部分求解即可．【详解】∵D为边BC 的中点，且S△ABC=4cm2，∴S△ADC=12S△ABC=2cm2，故选A．【点睛】本题考查了三角形中线的性质，熟练掌握三角形中线的性质是解答本题的关键．8．如图所示，在△ABC中，CD⊥BC于点C，则CD是△ABC（）A．AC边上的高B．AB边上的高C．BC边上的高D．以上都不对【答案】D【解析】【分析】根据三角形的一个顶点到它的对边所在直线的垂线段叫做这个三角形的高解答即可．【详解】解：CD 是△BCD 中BC 边上的高，而不是△ABC 的高．故选：D ．【点睛】本题考查了三角形的高线，熟练掌握三角形高线的定义是解答本题的关键．9．如图，AD 是ABC ∆的中线，DE AB ⊥于点E ，已知ABC ∆的面积是5，2AB =，则DE 的长为（ ）A ．52B ．53C ．54D ．1【答案】A【解析】【分析】 根据三角形的中线的性质得：ABD ∆的面积是2.5，再根据三角形的面积公式，即可求解．【详解】∵AD 是ABC ∆的中线， ABC ∆的面积是5，∴ABD ∆的面积是2.5，∵DE AB ⊥，2AB =， ∴ 2.52522DE ⨯==． 故选：A ．【点睛】本题主要考查三角形的中线的性质以及三角形的面积公式，掌握三角形的中线把三角形的面积平分，是解题的关键．10．如图，在ABC ∆中，点O 是ABC ∆内一点，且点O 到ABC ∆三边的距离相等．若40A ∠=︒，则BOC ∠的度数为（ ）A ．110︒B ．120︒C ．130︒D ．140︒【答案】A【解析】【分析】 根据三角形内角和定理得到△ABC+△ACB=140°，根据角平分线的性质得到BO 平分△ABC ，CO 平分△ACB ，根据三角形内角和定理计算即可．【详解】△△A=40°，△△ABC+△ACB=180°-40°=140°，△点O到△ABC三边的距离相等，△BO平分△ABC，CO平分△ACB，△△OBC+△OCB=12×（△ABC+△ACB）=70°，△△BOC=180°-70°=110°，故选：A．【点睛】本题考查的是角平分线的性质，三角形内角和定理，掌握角的平分线上的点到角的两边的距离相等是解题的关键．。

人教版八年级上册数学11.1 --11.3基础练习题11.1与三角形有关的线段一、选择题1.下面几个图形不具有稳定性的是A. B.C. D.2.已知a，b，c是的三条边长，化简的结果为A. B. C. 2c D. 03.长度分别为2，7，x的三条线段能组成一个三角形，x的值可以是A. 4B. 5C. 6D. 94.长为9，6，5，4的四根木条，选其中三根组成三角形，选法有A. 1种B. 2种C. 3种D. 4种5.下列各组数中，不可能成为一个三角形三边长的是A. 2，3，4B. 5，7，7C. 5，6，12D. 6，8，106.如图，在中，，G为AD的中点，延长BG交AC于E，F为AB上一点，于H，下面判断正确的有是的角平分线；是边AD上的中线；是边AD上的高；是的角平分线和高．A. 1个B. 2个C. 3个D. 4个7.如图，为估计池塘岸边A、B两点的距离，小方在池塘的一侧选取一点O，测得米，米，A、B间的距离不可能是A. 5米B. 10米C. 15米D. 20米8.若a、b、c为的三边长，且满足，则c的值可以为A. 5B. 6C. 7D. 89.下列说法错误的是A. 一般锐角三角形的三条高、三条中线、三条角平分线分别交于一点B. 钝角三角形有两条高在三角形外部C. 直角三角形只有一条高D. 任意三角形都有三条高、三条中线、三条角平分线10.三角形的高、中线和角平分线都是A. 直线B. 射线C. 线段D. 以上答案都不对11.如图，在中，AE是和AF分别是BC边上的中线和高线，AD是的平分线．则下列线段中最短的是A. AEB. ADC. AFD. AC12.如图，图中直角三角形共有A. 1个B. 2个C. 3个D. 4个二、填空题13.有四条线段，长分别为3cm、5cm、7cm、9cm，如果用这些线段组成三角形，可以组成______ 个三角形．14.如图，在中，D，E，F分别是BC，AD，CE的中点，且，则________．15.如图，D、E分别是边AB、BC上的点，，，设的面积为，的面积为，若，则的值为__．16.如图，在中，，，则以为内角的三角形是__________，以BC为边的三角形是___________，所对的边为___________．三、解答题17.如图，回答下列问题：图中有________个三角形，它们分别是______________________；以线段AD为边的三角形是__________________；线段CE所在的三角形是________，CE边所对的角是________．18.如图，在中，，CD是AB边上的高，且，，．求：的面积；的长．19.已知三角形的三条边为互不相等的整数，且有两边长分别为7和9，另一条边长为偶数．请写出一个三角形，符合上述条件的第三边长．若符合上述条件的三角形共有a个，求a的值．20.如图，在中，D、E分别是BC，AD的中点，，求．答案和解析1.【答案】A【解答】解：根据三角形的稳定性可得，B、C、D都具有稳定性．不具有稳定性的是A选项．故选A．2.【答案】D【解答】解：、b、c为的三条边长，，，原式．故选D．3.【答案】C【解答】解：由三角形三边关系定理得，即．因此，本题的第三边应满足，把各项代入不等式符合的即为答案．4，5，9都不符合不等式，只有6符合不等式，故选C．4.【答案】C【解答】解：四根木条的所有组合：9，6，5和9，6，4和9，5，4和6，5，4；根据三角形的三边关系，得能组成三角形的有9，6，5和9，6，4和6，5，4．故选C．5.【答案】C【解析】解：，三角形三边长为5，6，12不可能成为一个三角形，故选：C．6.【答案】B【解答】解：根据三角形的角平分线的概念，知AG是的角平分线，故此说法错误；根据三角形的中线的概念，知BG是的边AD上的中线，故此说法错误；根据三角形的高的概念，知CH为的边AD上的高，故此说法正确；根据三角形的角平分线和高的概念，知AH是的角平分线和高线，故此说法正确．故选B．7.【答案】A【解答】解：连接AB，根据三角形的三边关系定理得：，即：，、B间的距离在5和25之间，、B间的距离不可能是5米；故选：A．8.【答案】A【解答】解：，，；，；则，即，符合条件；故选A．9.【答案】C【解答】解：锐角三角形的三条高线、三条角平分线分别交于一点，故本选项说法正确；B.钝角三角形有两条高线在三角形的外部，故本选项说法正确；C.直角三角形也有三条高线，故本选项说法错误；D.任意三角形都有三条高线、中线、角平分线，故本选项说法正确；故选C．10.【答案】C【解答】解：三角形的高、中线和角平分线都是线段．故选C．11.【答案】C【解答】解：在中，AF是高，，又在中，AD是的平分线，AE是BC边上的中线，，，，故最短线段为AF．故选C．12.【答案】C【解析】【分析】本题考查了直角三角形的定义，比较简单，掌握直角三角形的定义是关键，要做到不重不漏．根据直角三角形的定义：有一个角是直角的三角形是直角三角形，可作判断．【解答】解：如图，，图中直角三角形有、、，共有3个．故选C．13.【答案】3【解析】解：其中的任意三条组合有3、5、7；3、5、9；3、7、9；5、7、9四种情况．根据三角形的三边关系，则其中的，不能组成三角形，应舍去，故可以组成3个三角形．故答案为：3．根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．此题考查了三角形的三边关系．判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数．14.【答案】【解答】解：点D，E，F，分别为BC、AD、CE的中点，且，，，，，故答案为．15.【答案】1【解答】解：，，，，．故答案为1．16.【答案】和；和；CD和AC．【解答】解：以为内角的三角形是和，以BC为边的三角形是和，所对的边为CD和AC，故答案为和；和；CD和AC．17.【答案】；，，，，，；，，；，．【解答】解：图中有6个三角形，它们分别是，，，，，．故答案为6；，，，，，；以线段AD为边的三角形是，，．故答案为，，；线段CE所在的三角形是，CE边所对的角是．故答案为，．18.【答案】解：的面积；的面积，．19.【答案】解：两边长分别为9和7，设第三边是a，则，即．第三边长是答案不唯一；，的值为4，6，8，10，12，14共六个，；20.【答案】解：、E分别是BC，AD的中点，，．11.2 与三角形有关的角一、选择题1. 已知在△ABC中，∠A＝70°，∠B＝60°，则∠C的度数为( )A．50°B．60°C．70°D．80°2. 在△ABC中，∠A，∠C与∠B处的外角的度数如图所示，则x的值是( )A．80 B．70 C．65D．603. 在Rt△ABC中，∠C＝90°，∠A－∠B＝50°，则∠A的度数为( )A．80°B．70°C．60°D．50°4.如图，点D在BC的延长线上，DE⊥AB于点E，交AC于点F.若∠A＝35°，∠D＝15°，则∠ACB的度数为( )A．65°B．70°C．75°D．85°5. 一个三角形三个内角的度数之比为2∶3∶4，这个三角形是()A. 直角三角形B. 等腰三角形C. 锐角三角形D. 钝角三角形6.若三角形的三个内角的度数之比为2∶3∶7，则这个三角形的最大内角是( )A．75°B．90°C．105°D．120°7. 如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC的度数为()A.118°B.119°C.120°D.121°8.如图，在△ABC中，D是∠ABC和∠ACB的平分线的交点，∠A＝80°，∠A BD＝30°，则∠BDC的度数为( )A．100°B．110°C．120°D．130°9.如图，把△ABC沿DE折叠，当点A落在四边形BCED内部时，∠A与∠1＋∠2之间有一种数量关系始终保持不变，这个关系是( )A．∠A＝∠1＋∠2 B．2∠A＝∠1＋∠2C．3∠A＝2∠1＋∠2 D．3∠A＝2(∠1＋∠2)10. 如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是()A.x=y+zB.x=y-zC.x=z-yD.x+y+z=180二、填空题11. 如图所示，在△ABC中，∠A=45°，∠B=60°，则外角∠ACD=.12. 有一张直角三角形纸片，记作△ABC，其中∠B=90°.按如图所示的方式剪去它的一个角，在剩下的四边形ADEC中，若∠1=165°，则∠2的度数为.13.如图，折叠一张三角形纸片，把三角形的三个角拼在一起，就可以说明一个几何定理．请你写出这个定理的内容：______________________.14. 如图所示，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，垂足分别为D，E.若∠AFD=158°，则∠EDF=°.15.定义：当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的一个内角为48°，那么“特征角”α的度数为____________．16.如图，在△ABC中，点E在BC的延长线上，∠ABC的平分线与∠ACE的平分线相交于点D.(1)若∠A＝70°，则∠ACE－∠ABC＝________°，∠D＝________°；(2)若∠A＝α，则∠ACE－∠ABC＝________，∠D＝________．三、解答题17.如图，用钢筋做支架，要求BA，DC相交所成的锐角为32°，现测得∠BAC＝∠DCA＝115°，则这个支架符合设计要求吗？为什么？18.如图，在△ABC中，AD是BC边上的高，E是AB上一点，CE交AD于点M，且∠DCM＝∠MAE.求证：△ACE是直角三角形．19. 在△ABC中，∠B＝55°，且3∠A＝∠B＋∠C，求∠A和∠C的度数.20.如图，在△ABC中，CD，BE分别是AB，AC边上的高，BE，CD相交于点O .(1)若∠ABC＝50°，∠ACB＝60°，求∠BOC的度数；(2)求证：∠BOC＋∠A＝180°.人教版八年级数学上册11.2 与三角形有关的角同步培优训练-答案一、选择题1. 【答案】A2. 【答案】B3. 【答案】B 又∵∠A－∠B＝50°，∴2∠A＝140°.∴∠A＝70°.4. 【答案】B ∴∠CFD＝∠AFE＝55°.∴∠ACB＝∠D＋∠CFD＝15°＋55°＝70°.5. 【答案】C6. 【答案】C 由题意，得2x＋3x＋7x＝180°，解得x＝15°.∴7x＝105°.7. 【答案】C∴∠ACB=180°-∠A-∠ABC=78°.∵∠ABC,∠ACB的平分线分别为BE,CD,∴∠FBC=∠ABC=21°,∠FCB=∠ACB=39°,∴∠BFC=180°-∠FBC-∠FCB=120°.故选C.8. 【答案】D ∴∠DBC＝∠ABD＝30°，∠ABC＝2∠ABD＝2×30°＝60°. ∴∠ACB＝180°－∠A－∠ABC＝40°.∵CD平分∠ACB，∴∠DCB＝12∠ACB＝12×40°＝20°.∴∠BDC＝180°－∠DCB－∠DBC＝130°.9. 【答案】B10. 【答案】A二、填空题11. 【答案】105°12. 【答案】105°所以∠1+∠2=360°-90°=270°. 因为∠1=165°，所以∠2的度数为105°.13. 【答案】三角形三个内角的和等于180°14. 【答案】68∴∠CFD=180°-∠AFD=180°-158°=22°.∵FD⊥BC，∴∠FDC=90°.∴∠C=180°-∠FDC-∠CFD=180°-90°-22°=68°.∵∠B=∠C，DE⊥AB，∴∠EDB=180°-∠B-∠DEB=180°-68°-90°=22°.∴∠EDF=180°-90°-22°=68°.15. 【答案】48°或96°或88°当β＝48°时，则“特征角”α＝2×48°＝96°；当第三个角为48°时，α＋12α＋48°＝180°，解得α＝88°.综上所述，“特征角”α的度数为48°或96°或88°.16. 【答案】(1)70 35 (2)α1 2α三、解答题17. 【答案】解：这个支架不符合设计要求．理由：如图，延长BA，DC交于点E.∵∠BAC＝∠DCA＝115°，∴∠EAC＝∠ECA＝65°.∴∠E＝180°－∠EAC－∠ECA＝50°. ∵要求BA，DC相交所成的锐角为32°，∴这个支架不符合设计要求．18. 【答案】证明：∵AD是BC边上的高，∴∠ADC＝90°.∵∠DCM＝∠MAE，∠CMD＝∠AME，∴∠AEC＝∠ADC＝90°.∴△ACE是直角三角形．19. 【答案】解：∵在△ABC中，∠A＋∠B＋∠C＝180°，3∠A＝∠B＋∠C，∴4∠A＝180°，解得∠A＝45°.∵∠B＝55°，∴∠C＝180°－45°－55°＝80°.20. 【答案】解：(1)∵CD⊥AB，BE⊥AC，∴∠BDC＝∠BEC＝90°.∵∠ABC＝50°，∠ACB＝60°.∴∠BCO＝40°，∠CBO＝30°.∴∠BOC＝180°－40°－30°＝110°.(2)证明：∵CD⊥AB，BE⊥AC，∴∠BDC＝∠BEC＝90°.∴∠ABE＝90°－∠A.∴∠BOC＝∠ABE＋∠BDC＝90°－∠A＋90°＝180°－∠A.∴∠BOC＋∠A＝180°.11.3多边形及其内角和一．选择题1．正多边形的每个内角为135度，则多边形为（）A．4 B．6 C．8D．102．若一个多边形减去一个角后，内角和为720°，则原多边形不可能是几边形（）A．四边形B．五边形C．六边形D．七边形3．一个四边形的四个内角度数之比为1：2：4：5，则这个四边形中，最小的内角为（）A．30°B．40°C．50°D．60°4．一个正多边形的每个内角的度数都等于相邻外角的2倍，则该正多边形的边数是（）A．3 B．4 C．6D．125．如图，已知一个五边形ABCDE纸片，一条直线将该纸片分割成两个多边形．若这两个多边形内角和分别为m和n，则m+n不可能是（）A．540°B．720°C．900°D．1080°6．如图，在五边形ABCDE中，AE∥BC，延长DE至点F，连接BE，若∠A=∠C，∠1 =∠3，∠AEF=2∠2，则下列结论正确的是（）①∠1=∠2 ②AB∥CD ③∠AED=∠A ④CD⊥DEA．1个B．2个C．3个D．4个7．如图，正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′，旋转角为α（0°＜α＜90°），若DE⊥B′C′，则∠α为（）A．36°B．54°D．72°8．如图，在四边形ABCD中，∠DAB的角平分线与∠ABC的外角平分线相交于点P，且∠D+∠C=210°，则∠P=（）A．10°B．15°C．30°D．40°9．设BF交AC于点P，AE交DF于点Q．若∠APB=126°，∠AQF=100°，则∠A-∠F=（）A．60°B．46°C．26°D．45°10．如图，已知四边形ABCD中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）A．90°B．135°C．270°D．315°11．如图，在六边形ABCDEF中，若∠A+∠B+∠C+∠D=500°，∠DEF与∠AFE的平分线交于点G，则∠G等于（）A．55°C．70°D．80°12．如图，A，B，C，D，E，F是平面上的6个点，则∠A+∠B+∠C+∠D+∠E+∠F的度数是（）A．180°B．360°C．540°D．720°二．填空题13．八边形的内角和为；一个多边形的每个内角都是120°，则它是边形．14．一个多边形，除了一个内角外，其余各角的和为2750°，则内角和是．15．如图，已知在四边形ABCD中，∠A+∠C=135°，∠ADE=125°，则∠B= ．16．如图所示，若∠DBE=78°，则∠A+∠C+∠D+∠E= °．17．如图所示，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= °．三．解答题18．（1）已知一个正多边形的每个内角比它的每个外角的4倍多30°，求这个多边形的边数；（2）一个多边形的外角和是内角和的七分之二，求这个多边形的边数．19．如图，在四边形ABCD中，BD⊥CD，EF⊥CD，且∠1=∠2．（1）求证：AD∥BC；（2）若BD平分∠ABC，∠A=130°，求∠C的度数．20．如图，四边形ABCD中，∠BAD=106°，∠BCD=64°，点M，N分别在AB，BC上，将△BMN沿MN翻折得△FMN，若MF∥AD，FN∥DC．求（1）∠F的度数；（2）∠D的度数．21．将纸片△ABC沿DE折叠使点A落在点A'处【感知】如图①，点A落在四边形BCDE的边BE上，则∠A与∠1之间的数量关系是；【探究】如图②，若点A落在四边形BCDE的内部，则∠A与∠1+∠2之间存在怎样的数量关系？并说明理由．【拓展】如图③，点A落在四边形BCDE的外部，若∠1=80°，∠2=24°，则∠A的大小为．22．已知，在四边形ABCD中，∠A+∠C=160°，BE，DF分别为四边形ABCD的外角∠CBN，∠MDC的平分线．（1）如图1，若BE∥DF，求∠C的度数；（2）如图2，若BE，DF交于点G，且BE∥AD，DF∥AB，求∠C的度数．参考答案1-5：CAACD 6-10:CBBBC 11-12:CB13、1080°；六14、2880°15、170°16、10217、72018、：（1）设这个多边形的每个内角是x°，每个外角是y°，则得到一个方程组得而任何多边形的外角和是360°，则多边形内角和中的外角的个数是360÷30=12，则这个多边形的边数是12边形；（2）设这个多边形的边数为n，依题意得：（n-2）180°=360°，解得n=9，答：这个多边形的边数为9．19、：（1）证明：∵BD⊥CD，EF⊥CD（已知），∴BD∥EF（垂直于同一直线的两条直线平行），∴∠2=∠3（两直线平行，同位角相等）．∵∠1=∠2，∴∠1=∠3（等量代换）．∴AD∥BC（内错角相等，两直线平行）．（2）∵AD∥BC（已知），∴∠ABC+∠A=180°（两直线平行，同旁内角互补）．∵∠A=130°（已知），∴∠ABC=50°．∵DB平分∠ABC（已知），∴∠3=25°．∴∠C=90°-∠3=65°．20、：（1）∵MF∥AD，FN∥DC，∠BAD=106°，∠BCD=64°，∴∠BMF=106°，∠FNB=64°，∵将△BMN沿MN翻折，得△FMN，∴∠FMN=∠BMN=53°，∠FNM=∠MNB=32°，∴∠F=∠B=180°-53°-32°=95°；（2）∠F=∠B=95°，∠D=360°-106°-64°-95°=95°．21、：（1）如图，∠1=2∠A．理由如下：由折叠知识可得：∠EA′D=∠A；∵∠1=∠A+∠EA′D，∴∠1=2∠A．（2）如图②，2∠A=∠1+∠2．理由如下：∵∠1+∠A′DA+∠2+∠A′EA=360°，∠A+∠A′+∠A′DA+∠A′EA=360°，∴∠A′+∠A=∠1+∠2，由折叠知识可得：∠A=∠A′，∴2∠A=∠1+∠2．（3）如图③，∵∠1=∠DFA+∠A，∠DFA=∠A′+∠2，∴∠1=∠A+∠A′+∠2=2∠A+∠2，∴2∠A=∠1-∠2=56°，解得∠A=28°．故答案为：∠1=2∠A；28°．22、：（1）过点C作CH∥DF，∵BE∥DF，∴BE∥DF∥CH，∴∠FDC=∠DCH，∠BCH=∠EBC，∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC，∵BE，DF分别为四边形ABCD的外角∠CBN，∠MDC的平分线，∴∠FDC=∠CDM，∠EBC=∠CBN，∵∠A+∠BCD=160°，∴∠ADC+∠ABC=360°160°=200°，∴∠MDC+∠CBN=160°，∴∠FDC+∠CBE=80°，∴∠DCB=80°；（2）连接GC并延长，同理得∠MDC+∠CBN=160°，∠MDF+∠NBG=80°，∵BE∥AD，DF∥AB，∴∠A=∠MDF=∠DGB=∠NBG=40°，∵∠A+∠BCD=160°，∴∠BCD=160°-40°=120°．。

专题三角平分线的性质与判定一、单选题1．如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若BC=15，且BD:CD=3:2，则点D到AB的距离为（）2345．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，AB+BC+CA=18，过O作OD⊥BC于点D，且OD=3，则△ABC的面积是．6．如图，AD∥BC，∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P，作PE⊥AB于点E．若PE7得8910．如图，△ABC中，∠ABC，∠ACB的角平分线交于点O，过O点作MN∥BC分别交AB，AC于M，N 两点，AB=6，ΔAMN的周长是15．则AC的长为．三、解答题11．如图1，△ABC的两条外角平分线AO，BO相交于点O，∠ACB=50°．(1)直接写出∠AOB的大小；(2)如图2，连接OC交AB于K．①求∠BCK的大小；②如图3，作AF⊥OC于F，若∠BAC=105°，求证：AB=2CF．12．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，若∠ABC=60°，FD=10，求DC的长．13．如图，四边形ABCD中，∠B=90°，AB∥CD，M是BC边上的一点，且AM平分∠BAD,DM平分∠ADC,求证：(1)BM=MC；(2)AM⊥MD．14．定义：如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．(1)如图1，△ABC中，AB=AC,∠A=36°，求证：△ABC是倍角三角形；(2)如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE=AB，若AB+AC=BD，请你找出图中的倍角三角形，并进行证明．15．如图，四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA，设∠ABC=α．(1)α=50°时，求∠DFC的度数；(2)证明：BE∥DF．16．在△ABC中，AO、BO分别平分∠BAC、∠ABC．(1)如图1，若∠C=32°，则∠AOB=________；(2)如图2，连结OC，求证：OC平分∠ACB；(3)如图3，若∠ABC=2∠ACB，AB=4，AC=7，求OB的长．17．如图，在△ABC中，D在BC边的延长线上，∠ACD的平分线CE交BA的延长线于点E，已知∠B=30°，∠E=40°，求证：AE=CE．18．如图，在四边形ABCD中，AB∥CD，∠C=90°，点E为BC的中点，DE平分∠CDA.(1)求证：AD=AB+CD；(2)若S△CDE=3，S△ABE=4，则四边形ABCD的面积为______.（直接写出结果）19．如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O与AB，AC分别相交于点M，N，且MN∥BC．(2)已知AB=7，AC=6，求△AMN的周长．参考答案题号12答案B B1．B【分析】本题考查的是角平分线的性质，作DE⊥AB于E，根据角平分线的性质得到CD=DE，根据题意求出CD的长即可．∵∴∵∴2∴3【详解】试题分析：本题需要分两种情况进行讨论：如图1所示：根据∠B=40°，∠C=70°可得：∠BAC=70°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=35°，则∠DAE=35°-20°=15°；如图2所示：根据∠B=40°，∠ACD=70°可得：∠BAC=30°，根据高线以及角平分线的性质可得：∠DAC=20°，∠EAC=15°，则∠DAE=15°+20°=35°.点睛：对于这种在三角形中求角度问题的时候，如果题目中没有给出图形，我们首先一定要根据题意画出图形，然后根据图形求出角的度数.特别要注意分类讨论的思想，在画图时一定要注意锐角三角形和钝角三角形两种情况.在画垂线的时候要注意高线在三角形内部和三角形外部两种情况.4．3：2【分析】过点D作DE⊥AB于点E，由角平分线的性质得到DE=CD，再根据三角形面积公式解答即可．【详解】解：过点D作DE⊥AB于点E，∵AD是Rt△ABC的角平分线，CD⊥AC,DE⊥AB∴DE=CDS△ABD S△ACD =12AB⋅DE12AC⋅CD=ABAC=128=32故答案为：3：2．【点睛】本题考查角平分线的性质、三角形面积公式等知识，是基础考点，掌握相关知识是解题关键．5．27【分析】作OE⊥AB于E,OF⊥AC于F，连接OA，根据角平分线的性质求出OE=OD=3和OF=OD=3，根据三角形面积公式计算即可．【详解】解：作OE⊥AB于E,OF⊥AC于F，连接OA，∵OB是∠ABC的平分线，OD⊥BC,OE⊥AB，∴OE=OD=3，同理OF=OD=3，∵AB+BC+CA=18．∴△ABC的面积=12×AB×3+12×AC×3+12×BC×3=27．故答案为：27．【点睛】本题主要考查角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．6．4【分析】根据角平分线的性质以及平行线的性质即可得出PM =PE =2，PE =PN =2，即可得出答案．【详解】解：过点P 作MN ⊥AD ，∵AD ∥BC ，∠ABC 的角平分线BP 与∠BAD 的角平分线AP 相交于点P ，PE ⊥AB 于点E ，∴AP ⊥BP ，PN ⊥BC ，∴PM =PE =2，PE =PN =2，∴MN =2+2=4．故答案为：4．7．2【分析】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，根据三角形的面积公式计算即可．【详解】连接PC 、PB 、PA ，作PD ⊥AB 于D ，PE ⊥AC 于E ，PF ⊥BC 于F ，由题意得，PE=PD=PF ， S △APC +S △APB +S △BPC =S △ACB ，∴12AC·PE+12AB·PD+12BC·PF=12AC·BC ，即12×12·PD+12×13•PD+12×5•PD=12×5×12，解得，PD=2，故答案为：2．【点睛】本题考查的是三角形的面积计算，掌握三角形的面积公式是解题的关键．8．60【分析】根据五边形的内角和求出∠BCD和∠CDE的和，再根据角平分线及三角形内角和求出∠CPD．【详解】解：∵五边形的内角和等于540°，∠A+∠B+∠E＝300°，∴∠BCD+∠CDE＝540°﹣300°＝240°，∵∠BCD、∠CDE的平分线在五边形内相交于点O，（∠BCD+∠CDE）＝120°，∴∠PDC+∠PCD＝12∴∠CPD＝180°﹣120°＝60°．故答案是：60．【点睛】本题解题的关键是知道多边形内角和定理以及角平分线的性质．9．5【分析】本题考查角平分线的性质定理，过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，利用角平分线的性质可得PF=PG=PE，然后根据三角形的面积求出PF=PE=PG=2，再利用△OMP的面积+△ONP的面积−△PMN的面积=4，进行计算即可解答．根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【详解】解：过点P作PE⊥OB，垂足为E，过点P作PF⊥MN，垂足为F，过点P作PG⊥OA，垂足为G，连接OP，∵MP平分∠AMN，NP平分∠MNB，∴PF=PG=PE，∵MN=1，△PMN的面积是1，∴ 12MN ⋅PF =1，∴PF =2，∴PG =PE =2，∵△OMN 的面积是4，∴△OMP 的面积+△ONP 的面积−△PMN 的面积=4，∴ 12OM ⋅PG +12ON ⋅PE−1=4，∴OM +ON =5．故答案为：5．10．9【分析】本题考查了等腰三角形的判定与性质，平行线的性质，根据角平分线的定义和平行线的性质可得△MOB 和△NOC 是等腰三角形，从而可得MO =MB ，NO =NC ，然后利用等量代换可得ΔAMN 的周长=AB +AC ，从而进行计算即可解答．【详解】解：∵BO 平分∠ABC ，CO 平分∠ACB ，∴∠ABO =∠OBC ，∠ACO =∠OCB ，∵MN ∥BC ，∴∠MON =∠OBC ，∠NOC =∠OCB ，∴∠ABO =∠MON ，∠ACO =∠NOC ，∴MO =MB ，NO =NC ，∵△AMN 的周长是15，∴AM +MN +AN =15，∴AM +MO +ON +AN =15∴AM +MB +NC +AN =15，∴AB +AC =15，∵AB =6，∴AC =15−6=9，故答案为：9．11．(1)65°；(2)①25°；②证明见解析．【分析】（1）根据三角形内角和定理求得∠CBA +∠CAB =130°，则∠EBA +∠BAD =230°，再由角平分线的定义求出∠OBA +∠OAB =115°，根据四边形内角和求出∠AOB 即可；（2）①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，根据角平分线的性质求解即可；②先求出KB=KC，过点A作AH∥BC交CO于点H，再求出KA=KH，则AB=CH，分别求出AH=AC，HF=CF，即可得出结论．【详解】（1）解：∵AO平分∠BAD，∴∠DAO=∠OAB，∵BO平分∠EOA，∴∠EBO=∠OBA，∵∠ACB=50°，∴∠CBA+∠CAB=130°，∴∠EBA+∠BAD=360°−130°=230°，∴∠OBA+∠OAB=115°，∴∠AOB=360°−50°−115°−130°=65°；（2）解：如图2，①过点O作OM⊥AD于点M，ON⊥BE于点N，OP⊥AB于点P，∵AO、BO分别平分∠DAB、∠EBA，∴OM=OP，OP=ON，∴OM=ON，∴CO平分∠ACB，∵∠ACB=50°，∴∠BCK=∠ACK=25°；②证明：∵∠BAC=105°，∠ACB=50°，∴∠ABC=25°，∵∠KCB=25°，∴∠KBC=∠KCE，∴KB=KC，如图3，过点A作AH∥BC交CO于点H，∴∠AHK=∠KCB，∠HAK=∠KBC，∴∠AHK=∠HAK，∴KA=KH，∴AB=CH，∵∠AHK=∠ACH，∴AH=AC，∵AF⊥CO，∴HF=CF，∴CH=2CF，∴AB=CH=2CF．12∴∵∴∴∵∴∴故DC=5．【点睛】此题主要考查了角平分线的定义，四边形内角和定理，含30°角的直角三角形的性质等知识，解题关键是熟练掌握各性质与定理．13．(1)见详解(2)见详解【分析】（1）作NM⊥AD，根据角平分线的性质得到BM=MN,MN=CM，等量代换得到答案．（2）根据平行线的性质得到∠BAD+∠ADC=180°，根据角平分线的定义得到∠MAD+∠ADM=90°，根据垂直的定义得到答案；【详解】（1）作NM⊥AD交AD于N，∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD,∵AM平分∠BAD,DM平分∠ADC,∴BM=MN,MN=CM,∴BM=CM；（2）证明：∵AB∥CD，∴∠BAD+∠ADC=180°,∵AM平分∠BAD,DM平分∠ADC,∴2∠MAD+2∠ADM=180°,∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM⊥DM；【点睛】本题考查的是角平分线的性质，掌握平行线的性质和角的平分线上的点到角的两边的距离相等是解题的关键．14．(1)见解析(2)△ADC和△ABC是倍角三角形，见解析【分析】（1）利用等边对等角及三角形的内角和求出∠B=∠C=72°，得到2∠A=∠C即可；（2）根据SAS证明△ABD≌△AED，得到∠ADE=∠ADB，BD=DE，证明CE=DE，得出∠C=∠BDE=2∠ADC，可得出∠ABC=2∠C．则结论得证．【详解】（1）证明：∵AB=AC，∴∠B=∠C，∵∠A+∠B+∠C=180°，∠A=36°，∴∠B=∠C=72°，∴2∠A=∠C，即△ABC是倍角三角形；（2）解：△ADC和△ABC是倍角三角形，证明如下：∵AD平分∠BAE，∴∠BAD=∠EAD，∵AB=AE，AD=AD，∴∴又∴∴∴∴∵15(2)∠EBC=∠DFC即可得出结论．【详解】（1）解：在四边形ABCD中，∠A=∠C=90°，∠ABC=α，α=50°，∴∠ADC=360°−∠A−∠C−∠ABC=130°，∵DF平分∠CDA，∠ADC=65°，∴∠FDC=12∴∠DFC =90°−65°=25°；（2）证明：在四边形ABCD 中，∠A =∠C =90°，∠ABC =α，∴∠ADC =360°−∠A−∠C−∠ABC =180°−α，∵DF 平分∠CDA ，∴∠FDC =12∠ADC =12(180°−α)，∴∠DFC =90°−12(180°−α)=12α，∵BE 平分∠ABC ，∴∠EBC =12α，∴∠EBC =∠DFC ，∴BE ∥DF ．16．(1)106°；(2)见解析；(3)3；【分析】（1）本题考查与角平分线有关的三角形内角和关系，根据∠C =32°得到∠CAB +∠CBA ，再结合角平分线求出∠CAO +∠CBO ，即可得到答案；（2）本题考查角平分线判定与性质，过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，根据角平分线性质得到OD =OF =OE ，结合角平分线的判定即可证明；（3）本题主要考查三角形全等的性质与判定，解题的关键是根据截长补短作出辅助线，在AC 上截取一点D ，使AD =AB ，连OD ，证明△ABO≌△ADO ，即可得到答案；【详解】（1）解：∵∠C =32°，∴∠CAB +∠CBA =180°−32°=148°，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴∠CAO +∠CBO =148°2=74°，∴∠AOB =180°−74°=106°；（2）证明：过O 作OD ⊥AC ，OE ⊥AB ，OF ⊥BC ，∵AO 、BO 分别平分∠BAC 、∠ABC ，∴OD =OF ，OD =OE ，∴OC 平分∠ACB ；（3）解：在AC 上截取一点D ，使AD =AB ，连OD ，设∠ACO =∠BCO =α，∵∠ABC =2∠ACB ，∴∠ABC =4α，∵BO 平分∠ABC ，∴∠ABO =∠CBO =2α，∵AO 平分∠BAC ，∴∠BAO =∠DAO ，在△ABO 与△ADO 中，AO =AO ∠BAO =∠DAO AB =AD，∴△ABO≌△ADO(SAS)，∴∠ABO =∠ADO =2α，OB =OD,AB =AD =4，又∵∠ACO =α，∴∠ACO =∠DCO =α，∴OD =OC =AC−AD =7−4=3，∴OB =3．17．证明见解析【分析】本题主要考查了角平分线的定义，三角形外角的性质以及等腰三角形的判定和三角形内角和定理的应用，根据外角的性质求出∠ECD=702，由角平分线的定义得∠ACE=∠ECD=70°，根据三角形内角和定理求出∠CAE=70°，可得∠ACE=∠CAE，从而可得结论．【详解】证明：∠B=30°，∠E=40°，∴∠ECD=∠B+∠E=70°，∵CE平分∠ACD，∴∠ACE=∠ECD=70°，在△ABE中，∠ACE+∠E+∠CAE=180°，∴∠CAE=180°−∠ACE−∠E=180°−70°−40°=70°，∴∠ACE=∠CAE，∴AE=CE．18．(1)见解析(2)14【分析】本题考查角平分线的性质，全等三角形的判定与性质．（1）过点E作EF⊥AD于F，根据角平分线的性质得出CE=EF，再证明△ABE≌△AFE，△CED≌△FED，根据全等三角形的性质得出AB=AF，DC=DF，进而得出结论；（2）由△ABE≌△AFE，△CED≌△FED，推出S△CED=S△FED，S△ABE=S△AFE，据此求解即可．【详解】（1）证明：如图，过点E作EF⊥AD于F，∵∠C=90°，AB∥CD，∴∠B=90°，∵DE平分∠CDA，∴CE=EF，∴Rt△CED≌Rt△FED(HL)，∴DC=DF，∵E是BC的中点，∴BE=CE，∴BE=EF，∵AE=AE，∴Rt△ABE≌Rt△AFE(HL)，∴AD=AF+FD=AB+CD；（2）解：∵△CED≌△FED，△ABE≌△AFE，∴S△CED=S△FED，S△ABE=S△AFE，∵S∴19(2)（（∴∴∴（∴∵∴∴∠BOM=∠ABO，∴BM=OM，同理可得：CN=ON，∴MN=OM+ON=BM+CN，∵AB=7，AC=6，∴△AMN的周长是AM+MN+AN=AM+BM+CN+AN=AB+AC=13．。

人教版八年级数学上册11.1--11.3能力测试题含答案（含答案）11.1 与三角形有关的线段考点1 三角形的认识及分类1．三角形是指( )A．由三条线段所组成的封闭图形B．由不在同一直线上的三条直线首尾顺次相接组成的图形C．由不在同一直线上的三条线段首尾顺次相接组成的图形D．由三条线段首尾顺次相接组成的图形2．如图中三角形的个数是( )A．6 B．7 C．8 D．93．在△ABC中，已知∠B=2∠C，∠A=30°，则这个三角形是( )A．锐角三角形B．直角三角形C．钝角三角形D．无法判断4．三角形按角分类可以分为（）A．锐角三角形、直角三角形、钝角三角形B．等腰三角形、等边三角形、不等边三角形C．直角三角形、等边直角三角形D．以上答案都不正确考点2 三角形的稳定性5．下列图形中具有稳定性的是（）A．直角三角形B．正方形C．长方形D．平行四边形6．下列图形中，不是运用三角形的稳定性的是（）A．房屋顶支撑架B．自行车三脚架C．拉闸门D．木门上钉一根木条7．如图，工人师傅做了一个长方形窗框ABCD，E，F，G，H分别是四条边上的中点，为了稳固，需要在窗框上钉一根木条，这根木条不应钉在( )A．G，H两点处B．A，C两点处C．E，G两点处D．B，F两点处考点3 三角形的三边关系8．下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )A ．3，3，6B ．1，5，5C ．1，2，3D ．8，3，49．如图，在△ABC 中，AC=5，中线AD=7，则AB 边的取值范围是( )A ．1AB 29<< B ．4AB 24<<C ．5AB 19<<D ．9AB 19<<10．一个三角形的两边长为4和7，第三边长为奇数，则第三边长可能为（ ）A ．5或7B ．5、7或9C ．7D ．1111．三角形的两边长分别为3和5，则周长C 的范围是（ ）A ．615C <<B ．616C << C ．1113C <<D ．1016C <<12．已知等腰△ABC 的两边长分别为2和3，则等腰△ABC 的周长为( )A ．7B ．8C ．6或8D ．7或813．已知a b c 、、是ABC ∆的三边长，化简a b c b a c +----的值是（ ）A ．2c -B ．22b c -C ．22a c -D ．22a b -考点4 三角形的高线14．下面四个图形中，线段BE是⊿ABC的高的图是（）A．B．C．D．15．如图，△ABC的面积计算方法是（）A．AC•BD B．12BC•EC C．12AC•BD D．12AD•BD16．下列各图中，AC边上的高画正确的是（）A．B．C．D．考点5 三角形的中线17．如图AD是△ABC的中线，那么BD=（）A．AD B．AC C．BC D．CD18．如图，AD 是ABC ∆的中线，5AB =，3AC =，ABD ∆的周长和ACD ∆的周长差为( )A ．6B ．3C ．2D ．不确定19．如图，已知在ABC 中，点D 、E 分别为BC 、AD 的中点，且26ABC S cm =△，则ABES △的值为（ ）A ．20.5cmB ．21.5cmC ．22cmD ．23cm20．如图，, , A B C 分别是线段1A B 、1B C 、1C A 的中点，若111A B C △的面积是20，那么ABC 的面积是（ ）A．4 B．103C．207D．5考点6 三角形的角平分线21．如图，△ABC中，AD为△ABC的角平分线，BE为△ABC的高，∠C=70°，∠ABC=48°，那么∠3是（）A．59°B．60°C．56°D．22°22．如图，在ABC中，∠A=60°，∠ABD和∠ACE是ABC的外角，∠ACE=110°，BF 平分∠ABD，则∠FBE=（）A．105°B．110°C．115°D．120°23．如图所示，在△ABC中，∠A＝36°，∠C＝72°，∠ABC的平分线交AC于D，则图中共有等腰三角形（）A．0个B．1个C．2个D．3个答案1．C2．C3．C4．A5．A6．C7．C8．B9．D10．B11．D12．D13．B14．A15．C16．D17．D18．C19．B20．C21．A22．C23．D11.2 与三角形有关的角班级：姓名：成绩：一、选择题1、将一副三角尺按如图所示的方式摆放，则∠a的大小为（）A． B． C． D．2、如图，∠ACD是△ABC的一个外角，CE平分∠ACD，F为CA延长线上的一点，FG∥CE，且FG交AB于点G.关于∠2＋∠3与∠1的大小关系，正确的是( )A．∠2＋∠3＞∠1 B．∠2＋∠3＜∠1 C. ∠2＋∠3＝∠1 D．无法判断3、用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应假设这个三角形中（）A. 有一个内角大于60°B. 有一个内角小于60°C. 每一个内角都大于60°D. 每一个内角都小于60°4、如图，在三角形ABC中，已知∠ABC=70º,∠ACB=60º,BE⊥AC于E,CF⊥AB于F,H是BE和CF的交点，则∠EHF=( )A. 100ºB. 110ºC. 120ºD.130º5、如图，在△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE交BD 于G，交BC于H，下列结论：①∠DBE=∠F；②2∠BEF=∠BAF+∠C；③∠F=（∠BAC﹣∠C）；④∠BGH=∠ABE+∠C其中正确的是（）A．①②③ B．①③④ C．①②④ D．①②③④6、如图，三角形ABC中，AB=AC，D，E分别为边A B，AC上的点，DM平分∠BDE，EN平分∠DEC，若∠DMN=110°，则∠DEA=（）A．40° B．50° C．60° D．70°7、如图，AD是∠CAE的平分线，∠B=300, ∠DAE=600，那么∠ACD等于（）A、900B、600C、800D、10008、在下列条件中，①∠A+∠B=∠C；②∠A：∠B：∠C=1：2：3；③∠A=∠B=∠C；④∠A=∠B=2∠C；⑤∠A=2∠B=3∠C，能确定△ABC为直角三角形的条件有A．2个 B．3个 C．4个 D．5个9、适合条件∠A=∠B=∠C的△ABC是（）A．锐角三角形 B．直角三角形 C．钝角三角形 D．等边三角形10、如图，D是△ABC的角平分线BD和CD的交点，若∠A=50°，则∠BDC=（）A．120° B．130° C．115° D．110°11、如图，CE是△ABC的外角∠ACD的平分线，若∠B=35°，∠ACE=60°，则∠A=（）A．35° B．95° C．85° D．75°12、将一副直角三角板，按如图所示叠放在一起，则图中∠α的度数是（）A.45°B.60°C.75°D.90°13、下列结论正确的是（）A.三角形的高总在三角形的内部B.△ABC的角平分线AD是自A出发的一条射线C.三角形中最大的内角不能小于60°D.三角形的三个外角中，最多只有一个钝角14、下列条件中，能判定△ABC为直角三角形的是（）A．∠A=2∠B=3∠C B．∠A+∠B=2∠C C．∠A=∠B=30° D．∠A=∠B=∠C15、如图，在五边形ABCDE中，AB＝AC＝AD＝AE，且AB∥ED，∠EAB＝120°，则∠DCB＝（）A．150° B．160° C．130° D．60°16、如图，在△ABC中，∠BAC=56°，∠ABC=74°，BP、CP分别平分∠ABC和∠ACB，则∠BPC=（）A．102° B．112° C．115° D．118°17、如图，把一副含30°角和45°角的直角三角板拼在一起，那么图中∠ADE是（）A．100°B．120° C．135° D．150°18、如图，△ABC的外角∠CBD和∠BCE的平分线相交于点F，则下列结论正确的是( )A.点F在BC边的垂直平分线上 B．点F在∠BAC的平分线上C．△BCF是等腰三角形 D．△BCF是直角三角形19、如图所示，∠1+∠2+∠3+∠4的度数为（）A100° B.180° C.360° D.无法确定20、如图，∠ABC=∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：①AD∥BC；②∠ACB=2∠ADB；③∠ADC=90°﹣∠ABD；④BD平分∠ADC；⑤∠BDC=∠BAC．其中正确的结论有（）A．2个 B．3个 C．4个 D．5个21、如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（）A．100° B．80° C．70° D．50°22、已知，如图，△ABC中，∠B=∠DAC，则∠BAC和∠ADC的关系是（）A．∠BAC＜∠ADC B．∠BAC=∠ADC C．∠BAC＞∠ADC D．不能确定二、填空题1、如图,在△ABC中,已知∠ABC=50°,∠ACB=60°,BE是AC边上的高,CF是AB边上的高,H 是BE和CF的交点,则∠BHC=______.2、如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=______.3、△ABC中，若∠A∶∠B∶∠C＝2∶3∶5，则∠A＝______，∠B＝______，∠C＝______．4、△ABC中，若∠A＋∠C＝2∠B，则∠B＝______．5、如图，△ABC中，∠BAC、∠ABC、∠ACB的外角分别记为∠α，∠β，∠γ，若∠α：∠β：∠γ=3：4：5，则∠BAC：∠ABC：∠ACB等于______°6、如图所示，已知△ABC的周长是22，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是______．7、如图，在△ABC中，∠B=40°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC=______．8、如图，∠A+∠B+∠C+∠D+∠E=______.三、解答题1、如图∠ABC=38°，∠ACB=100°，AD平分∠BAC，AE是BC边上的高，求∠DAE的度数．2、已知：如图，在△ABC中，∠1是它的一个外角，E为边AC上一点，延长BC到H，连接HE．求证：∠l>∠2．3、如图，在△ABC中，∠B＜∠ACB，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD，且PE交直线BC于点E.(1)若∠B＝35°，∠ACB＝85°，求∠E的度数；(2)当P点在线段AD上运动时，求证：∠E＝(∠ACB－∠B)．4、如图，在△ABC中，D是BC上一点，AD＝BD，∠C＝∠ADC，∠BAC＝57°，求∠DAC的度数．5、已知如图，在△ABC中，CH是外角∠ACD的角平分线，BH是∠ABC的平分线，∠A=58°，求∠H的度数．6、如图所示，在△ABC中，BP、CP分别是∠ABC和∠ACB的角平分线，∠BPC=134°，求∠A 的度数．参考答案一、选择题1-5、BCCDD6-10、AABBC11-15、CCCDA16-20、DCBCC21-22、AB二、填空题1、110°2、150°3、36°，54°，90°4、60°5、3:2:16、337、70°8、180三、解答题1、解：∵∠ABC=38°，∠ACB=100°(己知)∴∠BAC=180°―38°―100°=42°(三角形内角和180°) 又∵AD平分∠BAC(己知)∴∠BAD=21°∴∠ADE=∠ABC+∠BAD=59°(三角形的外角性质)又∵AE是BC边上的高，即∠E=90°∴∠DAE=90°―59°=31°2、证明：∵∠1是△ABC的一个外角∴∠1＞∠BCA∵∠BCA是△HEC的一个外角∴∠BCA＞∠2∴∠1＞∠23、 (1)解：∵∠B＝35°，∠ACB＝85°，∴∠BAC＝60°. ∵AD平分∠BAC，∴∠DAC＝30°.∴∠ADC＝65°.又∵PE⊥AD，∴∠DPE＝90°.∴∠E＝25°.(2)证明：∵∠B＋∠BAC＋∠ACB＝180°，∴∠BAC＝180°－(∠B＋∠ACB)．∵AD平分∠BAC，∴∠BAD＝∠BAC＝90°－(∠B＋∠ACB)．∴∠ADC＝∠B＋∠BAD＝90°－(∠ACB－∠B)．∵PE⊥AD，∴∠DPE＝90°.∴∠ADC＋∠E＝90°.∴∠E＝90°－∠ADC.∴∠E＝(∠ACB－∠B)．4、解：设∠DAC＝x，则∠BAD＝57°－x.∵∠C＝∠ADC，∴∠ADC＝(180°－x)．又∵AD＝BD，∴∠B＝∠BAD＝57°－x.∵∠ADC＝∠B＋∠BAD，∴(180°－x)＝2(57°－x)，解得x＝16°.即∠DAC的度数为16°.5、解：∵∠A=58°，∴∠ABC+∠ACB=180°﹣∠A=180°﹣58°=122°…①，∵BH是∠ABC的平分线，∴∠HBC=∠ABC，∵∠ACD是△ABC的外角，CH是外角∠ACD的角平分线，∴∠ACH=（∠A+∠ABC），∴∠BCH=∠ACB+∠ACH=∠ACB+（∠A+∠ABC），∵∠H+∠HBC+∠ACB+∠ACH=180°，∴∠H+∠ABC+∠ACB+（∠A+∠ABC）=180°，即∠H+（∠ABC+∠ACB）+∠A=180°…②，把①代入②得，∠H+122°+×58°=180°，∴∠H=29°．6、解：∵在△BPC中，∠BPC=134°，∴∠1+∠2=180°﹣∠BPC=180°﹣134°=46°，∵BP、CP分别是∠ABC和∠ACB的角平分线，∴∠ABC=2∠1，∠ACB=2∠2，∴∠ABC+∠ACB=2∠1+2∠2=2（∠1+∠2）=2×46°=92°，∴在△ABC中，∠A=180°﹣（∠ABC+∠ACB）=180°﹣92°=88°．11.3多边形及其内角和一．选择题（共12小题）1．如果一个n边形的外角和是内角和的一半，那么n的值为（）A．6 B．7 C．8 D．92．若一个多边形的内角和为1080°，则这个多边形的边数为（）A．6 B．7 C．8 D．93．多边形的内角和不可能为（）A．180°B．540°C．1080°D．1200°4．一个n边形的每一个外角都是72°，则n等于（）A．3 B．4 C．5 D．65．下列说法中，正确的个数有（）①若三条线段中有两条线段之和大于第三条线段，则以这三条线段为边可作一个三角形；②一个三角形中，至少有一个角不小于60°；③三角形的外角大于与它不相邻的任意一个内角；④一个多边形的边数每增加一条，这个多边形的内角和就增加180°．A．1个B．2个C．3个D．4个6．如图，足球图片正中的黑色正五边形的内角和是（）A．180°B．360°C．540°D．720°7．如图，五边形ABCDE的每个内角都相等，分别过顶点D、E作一条射线，交点为H，如果CD∥EH，那么∠DEH的度数是（）A．50°B．60°C．72°D．75°8．如图，七边形ABCDEFG中，AB、ED的延长线交于点O，若∠1，∠2，∠3，∠4相邻的外角的和等于230°，则∠BOD的度数是（）A．50°B．55°C．40°D．45°9．如图，把纸片△ABC的∠A沿DE折叠，点A落在四边形CBDE外，则∠1，∠2与∠A的关系是（）A．∠2-∠1=2∠A B．∠2-∠A=2∠1 C．∠1+∠2=2∠A D．∠1+∠A=2∠210．游戏中有数学智慧，找起点游戏规定：从起点走五段相等直路之后回到起点，要求每走完一段直路后向右边偏行，成功的招数不止一招，可助我们成功的一招是（）A．每走完一段直路后沿向右偏72°方向行走B．每段直路要短C．每走完一段直路后沿向右偏108°方向行走D．每段直路要长11．如图，五边形ABCDE中，AB∥CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则∠1+∠2+∠3=（）A．90°B．180°C．120°D．270°12．如图为互相垂直的两直线将四边形ABCD分成四个区域的情形，若∠A=100°，∠B=∠D=85°，∠C=90°，则根据图中标示的角，判断下列∠1，∠2，∠3的大小关系，何者正确（）A．∠1=∠2＞∠3 B．∠1=∠3＞∠2 C．∠2＞∠1=∠3 D．∠3＞∠1=∠2二．填空题（共5小题）13．一个正n边形的内角和是它外角和的4倍，则n= ．14．已知一个正多边形的内角和为1440°，则它的一个外角的度数为度．15．如图，正五边形ABCDE中，对角线AC与BE相交于点F，则∠AFE= 度．16．如图，在正五边形ABCDE中，DM是边CD的延长线，连接BD，则∠BDM的度数是．17．如图所示的六边形花环是用六个全等的直角三角形拼成的，则∠ABC= 度．三．解答题（共5小题）18．（1）已知一个正多边形的每个内角比它的每个外角的4倍多30°，求这个多边形的边数；（2）一个多边形的外角和是内角和的，求这个多边形的边数．19．小华与小明在讨论一个凸多边形的问题，他们的对话如下：小华说：“这个凸多边形的内角和是2020°．”小明说：“不可能吧！你错把一个外角当作内角了！”请根据俩人的对话，回答下列问题：（1）凸多边形的内角和为2020°，小明为什么说不可能？（2）小华求的是几边形的内角和？20．如图，在五边形ABCDE中，∠C=90°，∠D=70°，∠E=130°，AP平分∠EAB，BP平分∠ABC，求∠P的度数．21．如图，四边形ABCD中，∠BAD=106°，∠BCD=64°，点M，N分别在AB，BC上，将△BMN沿MN翻折得△FMN，若MF∥AD，FN∥DC．求（1）∠F的度数；（2）∠D的度数．22．已知，在四边形ABCD中，∠A+∠C=160°，BE，DF分别为四边形ABCD的外角∠CBN，∠MDC的平分线．（1）如图1，若BE∥DF，求∠C的度数；（2）如图2，若BE，DF交于点G，且BE∥AD，DF∥AB，求∠C的度数．参考答案1-5：ACDCC 6-10:CCAAA 11-12:BD13、1014、3615、7216、144°17、3018、（1）12；（2）9．19、：（1）∵n边形的内角和是（n-2）×180°，∴多边形的内角和一定是180°的整倍数．∵2020÷180=11……40，∴多边形的内角和不可能为2020°．（2）设小华求的是n边形的内角和，这个内角为x°，则0＜x＜180．根据题意，得（n-2）×180°-x+（180°-x）=2020°，解得n=∵n为正整数，∴2x+40必为180的整倍数．又∵0＜x＜180，∴∴n=13或14．∴小华求的是十三边形或十四边形的内角和．20、五边形ABCDE的内角和为（5-2）•180°=540°，∠C=90°，∠D=70°，∠E=130°，∴∠EAB+∠ABC=250°，∵AP平分∠EAB，BP平分∠ABC，∴∠PAB+∠PBA=125°，∴∠P=180°-125°=55°．21、：（1）∵MF∥AD，FN∥DC，∠BAD=106°，∠BCD=64°，∴∠BMF=106°，∠FNB=64°，∵将△BMN沿MN翻折，得△FMN，∴∠FMN=∠BMN=53°，∠FNM=∠MNB=32°，∴∠F=∠B=180°-53°-32°=95°；（2）∠F=∠B=95°，∠D=360°-106°-64°-95°=95°．22、：（1）过点C作CH∥DF，∵BE∥DF，∴BE∥DF∥CH，∴∠FDC=∠DCH，∠BCH=∠EBC，∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC，∵BE，DF分别为四边形ABCD的外角∠CBN，∠MDC的平分线，∴∠FDC=∠CDM，∠EBC=∠CBN，∵∠A+∠BCD=160°，∴∠ADC+∠ABC=360°160°=200°，∴∠MDC+∠CBN=160°，∴∠FDC+∠CBE=80°，∴∠DCB=80°；（2）连接GC并延长，同理得∠MDC+∠CBN=160°，∠MDF+∠NBG=80°，∵BE∥AD，DF∥AB，∴∠A=∠MDF=∠DGB=∠NBG=40°，∵∠A+∠BCD=160°，∴∠BCD=160°-40°=120°．。