六年级总复习组合图形面积经典习题

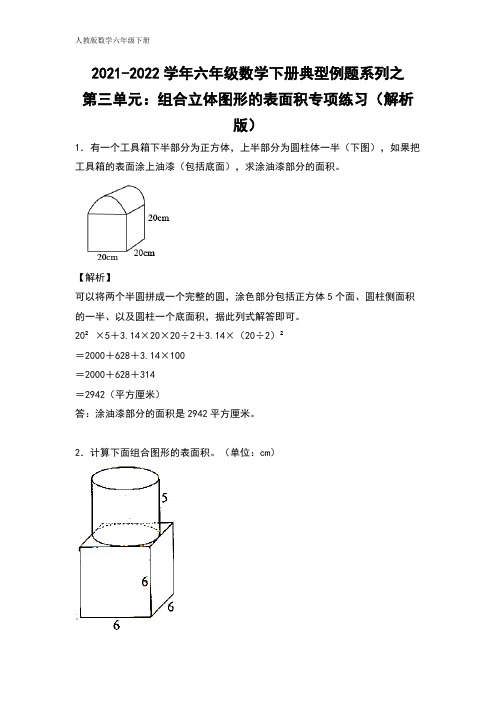
2021-2022学年六年级数学下册典型例题系列之第三单元：组合立体图形的表面积专项练习（解析版）1．有一个工具箱下半部分为正方体，上半部分为圆柱体一半（下图），如果把工具箱的表面涂上油漆（包括底面），求涂油漆部分的面积。

【解析】可以将两个半圆拼成一个完整的圆，涂色部分包括正方体5个面、圆柱侧面积的一半、以及圆柱一个底面积，据此列式解答即可。

20²×5＋3.14×20×20÷2＋3.14×（20÷2）²＝2000＋628＋3.14×100＝2000＋628＋314＝2942（平方厘米）答：涂油漆部分的面积是2942平方厘米。

2．计算下面组合图形的表面积。

（单位：cm）【解析】6×6×6+3.14×6×5，=216+94.2，=310.2（平方厘米）答：它的表面积是30.2平方厘米。

3．求下面图形的表面积和体积。

（单位：cm）【解析】表面积＝大正方体的表面积＋圆柱的侧面积，10×10×6＋3.14×4×6=600+75.36＝675.36（cm2）；4．下图是一个灯笼图片，阿姨做这个灯笼至少需要多大的彩纸？【解析】用外圆柱侧面积＋内圆柱侧面积＋上下两个圆环面积即可。

4÷2＝2（分米），2÷2＝1（分米）3.14×4×5＋3.14×2×5＋3.14×（22－12）×2＝62.8＋31.4＋3.14×3×2＝62.8＋31.4＋18.84＝113.04（平方分米）答：做这个灯笼至少需要113.04平方分米的彩纸。

5．有三个圆柱，一个堆在一个上面，底层圆柱最大，上层最小，它们的直径分别是4分米、 3分米、2分米，高都是2分米，这样的立体图形的表面积是多少？【解析】由图可知：这个立体图形的表面积等于最下面大圆柱的表面积加上上面两个小圆柱的侧面积。

六年级下册数学组合图形题总复习题精
选
1、求下列组合图形阴影部分的面积.
2、①求它的周长和面积.（单位：厘米）②圆的周长是18.84cm，求阴影部分面积.
③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积.
的半径是3cm，求阴影部分的周长和面积. （单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长. AB=40cm，求BC的长.
⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积.
求阴影部分的面积.
⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求
三角形AEF的面积.
⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积.（单位：cm）
部分面积64cm2，求梯形面积.
⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴.
部分12平方厘米，求阴影部分面积.
3、求下列图形的体积.（单位：厘米）。

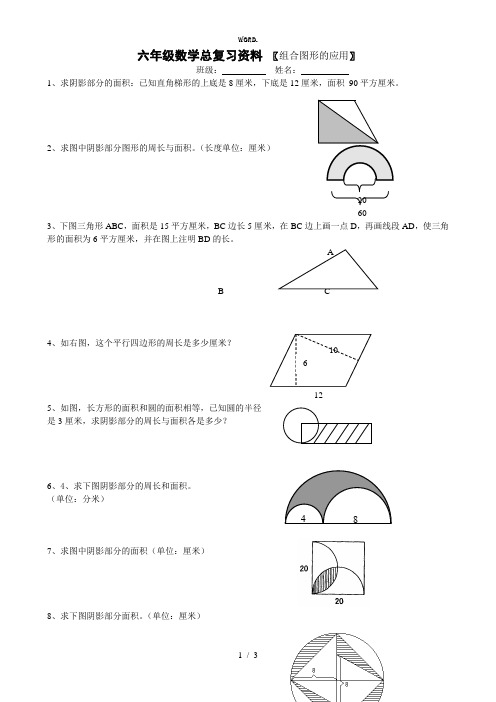
4 8 六年级数学总复习资料 〖组合图形的应用〗 班级： 姓名：1、求阴影部分的面积：已知直角梯形的上底是8厘米，下底是12厘米，面积 90平方厘米。

2、求图中阴影部分图形的周长与面积。

（长度单位：厘米）20603、下图三角形ABC ，面积是15平方厘米，BC 边长5厘米，在BC 边上画一点D ，再画线段AD ，使三角形的面积为6平方厘米，并在图上注明BD 的长。

AB C4、如右图，这个平行四边形的周长是多少厘米？125、如图，长方形的面积和圆的面积相等，已知圆的半径是3厘米，求阴影部分的周长与面积各是多少？6、4、求下图阴影部分的周长和面积。

（单位：分米）7、求图中阴影部分的面积（单位：厘米）8、求下图阴影部分面积。

（单位：厘米）6 109、三角形ABC的面积是24.6平方厘米，BF是FC的2倍，E是AC的中点，连接EF，求阴影部分的面积。

10、如右图，已知甲三角形面积为3.6平方厘米，乙三角形的面积为5.4平方厘米。

线段BD的长是DC的长的多少倍？11、下图是一个直角三角形，AD为底边BC上的高。

根据图中的已知条件，求出AD的长度。

(单位：厘米)12、如右图，已知直角三角形的面积是12平方厘米，求阴影部分面积。

13、有一块长20米，宽10米的长方形地，若在这块地四周修2米宽的小路，中间植草皮，草地面积是多少？小路的面积是多少？14、把一个四条边都是5厘米的平行四边形拉成一个正方形后，面积增加了7.5平方厘米，原平行四边形的高是多少？415、有一个正方形水池（如图的阴影部分），在它的周围修一条宽8米的花坛，花坛的面积是480平方米，水池的边长是多少米？16、如图，两个正方形的边长分别是4分米和3分米，阴影部分的面积是多少平方分米？17、求出下列各图中阴影部分图形的周长与面积：（单位；厘米）已改成-----------word 文本 --------------------- 方便更改。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

组合图形1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求
三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

4 8 六年级数学总复习资料 〖组合图形的应用〗 班级： 姓名：1、求阴影部分的面积：已知直角梯形的上底是8厘米，下底是12厘米，面积 90平方厘米。

2、求图中阴影部分图形的周长与面积。

（长度单位：厘米）20603、下图三角形ABC ，面积是15平方厘米，BC 边长5厘米，在BC 边上画一点D ，再画线段AD ，使三角形的面积为6平方厘米，并在图上注明BD 的长。

AB C4、如右图，这个平行四边形的周长是多少厘米？125、如图，长方形的面积和圆的面积相等，已知圆的半径是3厘米，求阴影部分的周长与面积各是多少？6、4、求下图阴影部分的周长和面积。

（单位：分米）7、求图中阴影部分的面积（单位：厘米）8、求下图阴影部分面积。

（单位：厘米）6 109、三角形ABC的面积是24.6平方厘米，BF是FC的2倍，E是AC的中点，连接EF，求阴影部分的面积。

10、如右图，已知甲三角形面积为3.6平方厘米，乙三角形的面积为5.4平方厘米。

线段BD的长是DC的长的多少倍？)11、下图是一个直角三角形，AD为底边BC上的高。

根据图中的已知条件，求出AD的长度。

(单位：厘米413、有一块长20米，宽10米的长方形地，若在这块地四周修2米宽的小路，中间植草皮，草地面积是多少？小路的面积是多少？14、把一个四条边都是5厘米的平行四边形拉成一个正方形后，面积增加了7.5平方厘米，原平行四边形的高是多少？15、有一个正方形水池（如图的阴影部分），在它的周围修一条宽8米的花坛，花坛的面积是480平方米，水池的边长是多少米？16、如图，两个正方形的边长分别是4分米和3分米，阴影部分的面积是多少平方分米？17、求出下列各图中阴影部分图形的周长与面积：（单位；厘米）3、迁移运用：学生快速阅读本组课文，想一想，通过再次阅读，还发现了哪些含义深刻的语句，自己是怎样读懂的。

4、总结：阅读时要认真体会、细细揣摩句子的言外之意，这样才能领会句子的真正意思。

A六年级数学总复习资料 〖组合图形的应用〗班级： 姓名：1、求阴影部分的面积：已知直角梯形的上底是 8 厘米，下底是 12 厘米，面积 90 平方厘米2、求图中阴影部分图形的周长与面积 （长度单位：厘米）603、下图三角形 ABC ，面积是 15 平方厘米，BC 边长 5 厘米，在 BC 边上画一点 D ，再画线段 AD ，使三 角形的面积为 6 平方厘米，并在图上注明 BD 的长BC4、如右图，这个平行四边形的周长是多少厘米125、如图，长方形的面积和圆的面积相等，已知圆的半径 是 3 厘米，求阴影部分的周长与面积各是多少6、4、求下图阴影部分的周长和面积 （单位：分米）7、求图中阴影部分的面积（单位：厘米）8、求下图阴影部分面积 （单位：厘米）4820 10 69、三角形ABC 的面积是24.6 平方厘米，BF 是FC 的2 倍，E 是AC 的中点，连接EF，求阴影部分的面积10、如右图，已知甲三角形面积为3.6 平方厘米，乙三角形的面积为5.4 平方厘米线段BD 的长是DC 的长的多少倍11、下图是一个直角三角形，AD 为底边BC 上的高根据图中的已知条件，求出AD 的长度(单位：厘米)12、如右图，已知直角三角形的面积是12 平方厘米，求阴影部分面积13、有一块长20 米，宽10 米的长方形地，若在这块地四周修2 米宽的小路，中间植草皮，草地面积是多少小路的面积是多少14、把一个四条边都是5 厘米的平行四边形拉成一个正方形后，面积增加了7.5 平方厘米，原平行四边形的高是多少215、有一个正方形水池（如图的阴影部分），在它的周围修一条宽8 米的花坛，花坛的面积是480 平方米，水池的边长是多少米16、如图，两个正方形的边长分别是4 分米和3 分米，阴影部分的面积是多少平方分米17、求出下列各图中阴影部分图形的周长与面积：（单位；厘米）4 6小学试题认真做好每一份试题，给读者带来方便是我们的宗旨，谢谢你的下载!3。

六年级数学组合图形的面积试题1.右图是一个方格网，计算阴影部分的面积．【答案】4【解析】扩展法．把所求三角形扩展成正方形ABCD中．这个正方形中有四个三角形：一个是要求的；另外三个分别是：ABE、FEC、DAF，它们都有一条边是水平放置的，易求它们的面积分别为，，．所以，图中阴影部分的面积为：()．2.两个边长相等的正方形各被分成25个大小相同的小方格．现将这两个正方形的一部分重叠起来，若左上角的阴影部分(块状)面积为，右下角的阴影部分(线状)面积为，求大正方形的面积．【答案】19【解析】块状部分与线状部分之间的部分称为D，则D与前者共14个方格，与后者共17个方格，因此每个方格的面积是大正方形的面积为．3.把大正三角形每边八等分，组成如右图所示的三角形网．如果大三角形的面积是128，求图中粗线所围成的三角形的面积．【答案】52【解析】图中有(个)小三角形，那么一个小三角形的面积是，图形内部格点数为12，图形周界上格点数为4；图形的面积为：(面积单位)，进而得图形的面积为：．4.如图，每一个小方格的面积都是1平方厘米，那么用粗线围成的图形的面积是多少平方厘米？【答案】6.5【解析】方法一：正方形格点阵中多边形面积公式：(N+-1)×单位正方形面积，其中N为图形内格点数，L为图形周界上格点数．有N=4，L=7，则用粗线围成图形的面积为：(4+-1)×1=6．5(平方厘米)方法二：如右上图，先求出粗实线外格点内的图形的面积，有①=3÷2=1．5，②=2÷2=1，③=2÷2=1，④=2÷2=1，⑤=2÷2=l，⑥=2÷2=1，还有三个小正方形，所以粗实线外格点内的图形面积为1．5+l+1+1+1+1+3=9．5，而整个格点阵所围成的图形的面积为16，所以粗线围成的图形的面积为：16-9．5=6．5平方厘米．5.如图，在角的两边上分别有、、及、、六个点，并且、、、、的面积都等于1，则的面积等于多少？【答案】【解析】根据题意可知，，所以，．6.如图，是一个四边形，、分别是、的中点．如果、与的面积分别是6、7和8，且图中所有三角形的面积均为整数，则四边形的面积为多少．【答案】60【解析】连接、、．由于是的中点，所以与的面积相等，而比的面积大1，所以比的面积大1；又由于是的中点，所以的面积与的面积相等，那么的面积比的面积大1，所以的面积为9．假设的面积为，则的面积为．根据几何五大模型中的蝴蝶定理，可知的面积为，的面积为．要使这两个三角形的面积为整数，可以为1，3或7．由于的面积为面积的一半，的面积为面积的一半，所以与的面积之和为四边形面积的一半，所以与的面积之和等于四边形的面积，即：，得．将、3、7分别代入检验，只有时等式成立，所以的面积为7，、、的面积分别为8、6、9．四边形ABCD的面积为．小结：本题中“且图中所有三角形的面积均为整数”这个条件是多余的．7.如下图，长方形和长方形拼成了长方形，长方形的长是20，宽是12，则它内部阴影部分的面积是多少．【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半，为．8.在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．9.如图，三角形ABC的面积是24，D、E和F分别是BC、AC和AD的中点．求三角形DEF的面积．【答案】3【解析】三角形ADC的面积是三角形ABC面积的一半，三角形ADE又是三角形ADC面积的一半．三角形FED的面积是三角形ADE面积的一半，所以三角形FED的面积．10.在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分的面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如上图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．。