高一数学 初升高衔接班 第六讲 一元二次不等式的解法讲义
- 格式:doc
- 大小:219.50 KB
- 文档页数:7



![高一数学最新课件-一元二次不等式解法[整理] 精品](https://img.taocdn.com/s1/m/c9bfe74ba0116c175e0e482e.png)

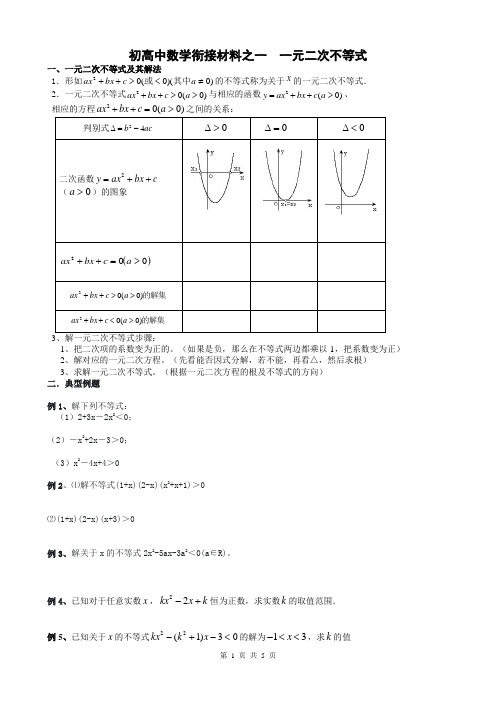
初高中数学衔接材料之一 一元二次不等式一、一元二次不等式及其解法1.形如)0)(0(02≠<>++a c bx ax 其中或的不等式称为关于x 的一元二次不等式.2.一元二次不等式20(0)ax bx c a ++>>与相应的函数2(0)y ax bx c a =++>、相应的方程2之间的关系:1、把二次项的系数变为正的。
(如果是负,那么在不等式两边都乘以-1,把系数变为正)2、解对应的一元二次方程。
(先看能否因式分解,若不能,再看△,然后求根)3、求解一元二次不等式。
(根据一元二次方程的根及不等式的方向)二.典型例题例1、解下列不等式:(1)2+3x -2x 2<0;(2)-x 2+2x -3>0;(3)x 2-4x+4>0例2、⑴解不等式(1+x)(2-x)(x 2+x+1)>0⑵(1+x)(2-x)(x+3)>0例3、解关于x 的不等式2x 2-5ax-3a 2<0(a ∈R)。
例4、已知对于任意实数x ,22kx x k -+恒为正数,求实数k 的取值范围.例5、已知关于x 的不等式22(1)30kx k x -+-<的解为13x -<<,求k 的值例6、已知关于x 的不等式22k kx x ->+的解为12x >-,求实数k 的值.例7、已知A={}2|320x x x -+ ,B={}2|(1)0x x a x a -++ 。
(1)若B A ,求a 的取值范围;(2)若A ∩B 是单元素集合,求a 取值范围。
例8.解关于x 的不等式:⑴2(2)20x a x a +--<⑵210ax ax ++三.练习题练习一、解下列一元二次不等式:1、0672≥+-x x2、0122<--x x3、0122>-+x x4、x+2>3x 25、01242<--x x6、012532>-+x x7、25160x x ++>8、260x x -+9、2690x x ++10、0121632>-+x x11、0123732>+-x x12、071522≤++x x13、0442>-+-x x14、2230x x --+≥15、0262≤+--x x16、0532>+-x x17、2230x x -+-≥18、2620x x -+-练习二1、若02522>-+-x x ,则221442-++-x x x 等于( ) A .54-x B .3- C .3 D .x 45-2、若10<<a ,则不等式0)1)((>--ax x a 的解是( ) A. a x a 1<< B. a x a<<1 C. a x 1>或a x < D. a x 1<或a x > 3、若不等式022>++bx ax 的解集⎭⎬⎫⎩⎨⎧<<-3121|x x 则a -b 值是( ) A .-10 B .-14 C .10 D .144、已知不等式250ax x b -+>的解集为{|32}x x -<<,则不等式250bx x a -+>的解集为( ) A .11{|}32x x -<< B .11{|}32x x x <->或 C .{|32}x x -<< D .{|32}x x x <->或 5、若关于x 的不等式4104822<<>---x a x x 在内有解,则实数a 的取值范围是( )A .4-<aB .4->aC .12->aD .12-<a二、填空题1、不等式9)12(2≤-x 的解集为___________________________。
第六讲一元二次不等式的解法
一、一元二次不等式及其解法
【知识讲解】
1、定义:形如ax2+bx+c>0(a>0)(或ax2+bx+c<0(a>0))的不等式叫做关于x 的一元二次不等式。
2、一元二次不等式的一般形式:
ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0)
3、一元二次不等式的解集:
4、解一元二次不等式的一般步骤:
(1)将原不等式化成一般形式ax2+bx+c>0(a>0)(或ax2+bx+c<0(a>0));
(2)计算Δ=b2-4ac;
(3)如果Δ≥0,求方程ax2+bx+c=0(a>0)的根;若Δ<0,方程ax2+bx+c=0(a >0)没有实数根;
(4)根据上表,确定已经化成一般形式的不等式的解集,即为原不等式的解集。
二.典型例题
例1、解下列不等式:
(1)2+3x -2x 2<0; (2)-x 2+2x -3>0; (3)x 2
-4x +4>0
例2、⑴解不等式(1+x )(2-x )(x 2
+x +1)>0 ⑵(1+x )(2-x )(x +3)>0
例3、解关于x 的不等式2x 2-5ax -3a 2
<0(a ∈R)。
例4、已知对于任意实数x ,2
2kx x k -+恒为正数,求实数k 的取值范围.
例5、已知关于x 的不等式22
(1)30kx k x -+-<的解为13x -<<,求k 的值
例6、已知关于x 的不等式2
2k kx x ->+的解为1
2
x >-
,求实数k 的值.
例7、已知A={}2
|320x x x -+?,B={}2|(1)0x x a x a -++?。
(1)若B A ,求a 的取值范围;
(2)若A∩B 是单元素集合,求a 取值范围。
例8.解关于x 的不等式:
⑴2(2)20x a x a +--< ⑵012
>++ax ax
三.练习题
练习一、解下列一元二次不等式:
1、0672≥+-x x
2、0122<--x x
3、0122>-+x x
4、x+2>3x 2
5、01242<--x x
6、012532>-+x x
7、25160x x ++> 8、260x x -+?
9、2690x x ++? 10、0121632>-+x x
11、0123732>+-x x 12、071522≤++x x
13、0442>-+-x x 14、2230x x --+≥
15、0262≤+--x x 16、0532>+-x x
17、2230x x -+-≥ 18、2620x x -+-?
练习二
1、若02522
>-+-x x ,则221442
-++-x x x 等于( )
A .54-x
B .3-
C .3
D .x 45- 2、若10<<a ,则不等式0)1
)((>-
-a
x x a 的解是( ) A. a
x a 1<
<
B.
a x a
<<1
C. a x 1>或a x <
D. a
x 1
<或a x >
3、若不等式022
>++bx ax 的解集⎭⎬⎫⎩
⎨⎧<<-3121|x x 则a -b 值是( )
A .-10
B .-14
C .10
D .14
4、已知不等式2
50ax x b -+>的解集为{|32}x x -<<,则不等式2
50bx x a -+>的解集
为( ) A .11
{|}32
x x -
<< B . 1
1{|}32
x x x <->或 C .{|32}x x -<<
D .{|32}x x x <->或
5、若关于x 的不等式4104822
<<>---x a x x 在内有解,则实数a 的取值范围是( )
A .4-<a
B .4->a
C .12->a
D .12-<a
二、填空题
1、不等式9)12(2≤-x 的解集为___________________________。
2、不等式0<x 2+x -2≤4的解集是_______________ .
3、若不等式2(2)2(2)40a x a x -+--<对一切x R ∈恒成立,则a 的取值范围是______________. 三、简答题:
1、解关于x 的不等式:
(1)0322
2
<--a ax x (2)0)1(2<--+a x a x
2、2
0x ax a ++?
练习三
1.不等式|x(x+1)| >x(x+1)的解集是( ) (A )(-∞,-1)∪(-1,+∞) (B )(-1,+∞) (C )(-∞,-1)∪(-1,0) (D )(-1,0)
2.不等式
<0的解集是( )
(A )(0,3) (B )(-3,0) (C )(-3,3) (D )R
3.若关于x 的不等式ax 2
+bx+c <0(a≠0)的解集为F ,那么( )
(A )a <0,且b 2-4ac >0 (B )a <0,且b 2
-4ac≤0
(C )a >0,且b 2-4ac≤0 (D )a >0,且b 2
-4ac >0
4.有三个关于x 的方程:2
40x ax -+=,2
(1)160x a x +-+=,
223100x ax a +++=,已知其中至少有一个方程有实根,则实数a 的取值范围为
( )
(A )-4≤a≤4 (B )-2<a <4 (C )a <0 (D )a≤-2,或a≥4
5.不等式4≤x 2
-3x <18的整数解集是 。
6.若方程组2222
x y x y m ìï+=ïí
ï+-=ïî有两组解,则实数m 的取值集合是 。
7.集合A={}2|340x x x --?,B={}2
|260x x x -->,则
A∩B= 。
89.若
2
180x x q p
++>的解集是{x|2<x <4},则p ,q 的值分别是p= ,q= 。
9.对任何实数x ,函数的值恒为负数,则p 的取值范围
是 。
10、 解下列不等式:
(1)4x 2
-4x >15; (2)-x 2
-2x +3>0; (3)4x 2
-4x +1<0
11、自变量x 在什么范围取值时,函数y =-3x 2
+12x -12的值等于0?大于0?小于0?
12、若关于x 的方程x 2
-(m +1)x -m =0有两个不相等的实数根,求m 的取值范围。
13、解下列不等式:
(1)4x 2
-4x <15; (2)-x 2
-2x +3<0; (3)4x 2
-4x +1>0
(3)4x2-20x<25;(4)-3x2+5x-4>0;(5)x(1-x)>x(2x-3)+10 14、m是什么实数时,关于x的方程mx2-(1-m)x+m=0没有实数根?
15、已知函数y=1
2
x2-3x-
3
4
,求使函数值大于0的x的取值范围。