有理数的乘方(1)

七年级数学《有理数的乘方（一）》教学设计分）到不同的发展，同时，及时反馈教学效果，随时调节教学进程。

教学程序问题与情境师生互动设计意图及媒体应用分析活动一创设情境，导入新课问题1：把一张纸对折2次可裁成几张？你能用算式表示吗？对3次呢？若对折10次可裁成几张？怎样用一个算式表示（不用算出结果）？若对折100次，算式中有几个2相乘？问题2：对折100次裁成的张数，可用算式表示，在这个积中有100个2相乘。

这么长的算式有简单的记法吗？【教师活动】（1）用一张纸边演示操作，边用课件出示问题1；（2）鼓励学生操作并猜测，在小组内讨论交流。

（3）关注并适时评价学生的表现。

结合学生回答板书：对折2次可以裁成2×2张；对折3次可以裁成2×2×2张；对折10次可以裁成2×2×2×2×2×2×2×2×2×2；对折100次的裁成的张数就是100个2相乘，黑板上能写下吗？有没有简单的记法呢？这就是本节课要研究的内容（揭示并板书课题）。

【学生活动】（1）动手操作感知问题，大胆提出猜想。

（2）将自己的猜想在小组内交流探讨，（1）问题旨在帮助学生认识数学与生活的密切关系，激发求知欲。

（2）学生自己动手折纸是为了获得亲身体验和感知问题，激发探索欲。

（3）通过独立思考大胆猜测、同伴讨论交流、代表发言让学生感受多种情感体验，并进一步理解问题。

【媒体应用分析】PPT课件出示问题1、2，引导学生理解建构乘方意义的必要性，为进一步探究乘方意义及运算打下伏笔。

教学反思：。

1.5.1有理数的乘方（1）导学目标: 1、理解有理数乘方的意义；2、掌握有理数乘方运算；3、经历探索有理数乘方的运算，获得解决问题经验；导学重点：有理数乘方的运算。

导学难点：有理数乘方的运算。

导学指导：一、改变旧世界1、看下面的故事：从前，有个“聪明的乞丐”他要到了一块面包。

他想，天天要饭太辛苦，如果我第一天吃这块面包的一半，第二天再吃剩余面包的一半，……依次每天都吃前一天剩余面包的一半，这样下去，我就永远不要去要饭了！请你们交流讨论，再算一算，如果把整块面包看成整体“1”，那第十天他将吃到面包。

2、拉面馆的师傅用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复多次，就能把这根很粗的面条，拉成许多很细的面条.想想看，捏合次后，就可以拉出32根面条.二、知识新天地1、分小组合作导学P41页内容，然后再完成好下面的问题1）叫乘方，叫做幂，在式子ａｎ中 ,ａ叫做，ｎ叫做2）式子ａｎ表示的意义是3）从运算上看式子ａｎ，可以读作，从结果上看式子ａｎ，可以读作；2、将下列各式写成乘方（即幂）的形式：（1）（-2）×（-2）×（-2）×（-2）＝.（2）、（—14）×（—14）×（—14）×（—14）＝；（3）x•x•x•……•x（2010个）＝3、例题，P41例1师生共同完成从例题1 可以得出：负数的奇次幂是数，负数的偶次幂是数，正数的任何次幂都是数，0的任何正整次幂都是；4、思考：（—2）4和—24意义一样吗？为什么？2019.4 5、自学例2 （教师指导）三、学海苦无边完成P42页1，2.四、金秋烂漫时：五、万里长征路1、我们已经导学了五种运算，请把下表补充完整：2、用乘方的意义计算下列各式：（1）42-；（2）323⎛⎫- ⎪⎝⎭ ； （3）223-；3.计算(1) 2221(2)2(10)4----⨯-； (2) 3212(0.5)(2)(8)2⎛⎫-⨯-⨯-⨯- ⎪⎝⎭；1.5.1有理数的乘方（2）导学目标: 1、能确定有理数加、减、乘、除、乘方混合运算的顺序；2、会进行有理数的混合运算；3、培养并提高正确迅速的运算能力；导学重点：运算顺序的确定和性质符号的处理；导学难点：有理数的混合运算；导学指导一、改变旧世界1、在2+×（－6）这个式子中，存在着 种运算。

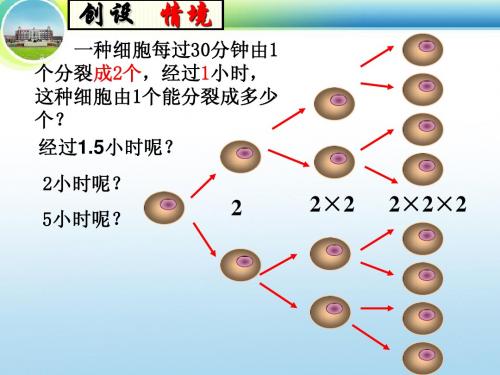
●课题有理数的乘方（一）●教学目标（一）教学知识点1．有理数乘方的意义．2．能进行有理数的乘方运算．（二）能力训练要求1．在现实背景中，理解有理数乘方的意义．2．能进行有理数的乘方运算．（三）情感与价值观要求通过师生共同交流，渗透利用数学知识解决实际问题的思想，以激发学生学习的兴趣，树立解决问题的信心．●教学重点有理数乘方的意义．●教学难点1．理解有理数乘方的意义上有困难．2．合理进行乘方运算．●教学方法讲练结合法●教具准备细胞分裂示意图投影片四张第一张：练习（记作§2．10．1 A）第二张：例1（记作§2．10．1 B）第三张：例2（记作§2．10．1 C）第四张：法则（记作§2．10．1 D）●教学过程Ⅰ．创设情景问题，引入课题［师］我们知道，每个生物体都是由细胞组成．动物由动物细胞组成，植物由植物细胞组成．活的细胞和生物体一样，也经过生长、衰老、死亡几个阶段．细胞本身的繁殖是以细胞分裂方式进行的．大家来观察一幅某种细胞分裂示意图：（出示“细胞分裂示意图”）这种细胞每过30分钟便由1个分裂成2个．想一想：经过5小时，这种细胞由1个能分裂成多少个？［生］1个细胞30分钟后分裂成2个，1个时分裂成4个，1．5小时后分裂成8个，2小时后分裂成16个，……，5小时后，这种细胞由1个能分裂成1024个．［师］对，1个细胞30分钟后分裂成2个，这是第一次分裂；1小时后分裂成4个，可以写成2×2，这是第二次分裂，1．5小时后分裂成8个，可写成2×2×2，这是第三次分裂，2小时后分裂成16个，也可写成2×2×2×2，这是第四次分裂，依次类推，想一想：5小时要分裂多少次？［生甲］5小时要分裂10次．［生乙］老师，我知道了，经过一次细胞分裂，1个可分裂成2个，经过二次分裂，1个可分裂成2×2个，经过三次分裂，1个可分裂成2×2×2个，这样依次类推，经过十次这样的分裂，1个便可分裂成［师］乙同学分析得很好，经过十次分裂后，1个细胞可以分裂成：个，但10个2相乘写起来挺麻烦的，为了简便，可将记为210，210表示有10个2相乘，我们把这种运算叫乘方．今天我们就来探讨有理数的乘方．Ⅱ．讲授新课［师］在小学中，我们把a×a记作a2，读作a的平方，或a的二次方．想一想：a×a 表示什么？［生］表示边长为a的正方形面积．［师］对，还把a×a×a记作a3，读作a的立方，或a的三次方．那a×a×a表示什么？［生］表示棱长为a的正方体的体积．［师］很好，刚才我们又把记作210．一般地，我们有：n个相同的因数a相乘，记作a n，即：这种求n个相同因数a的积的运算叫做乘方（Power）．乘方的结果叫做幂（Power）．在a n中，a叫做底数（base number）．n叫做指数（exponent）．a n读作a的n次方．a n看作是a的n 次方的结果时，也可读作a 的n 次幂．在这儿需要注意：乘方是一种运算，幂是乘方运算的结果．如：在94中，底数是9，指数是4，94读作9的4次方，或9的4次幂． 下面我们做一练习来熟悉这些概念（出示投影片§2．10 A ），口答： 1．填空： （1）（－1）12的底数是_____，指数是_____． （2）（－3）11表示_____个_____相乘． （3）（－21）5的指数是_____，底数是_____． （4）7．54的指数是_____，底数是_____． ［生］（－1）12的底数是－1，指数是12． （－3）11表示11个－3相乘． （－21）5的指数是5，底数是－21， 7．54的指数是4，底数是7．5．［师］很好．那5的底数是什么？指数是什么？ ［生］5的底数是5，没有指数． ［师］对吗？ ……［师］在这里需要注意：一个数可以看成这个数本身的一次方．如：5就是51，指数1通常省略不写．大家也可以这样理解：指数就是指相乘的因数的个数，指数是1，就是指只有一个因数．a n 就是n 个a 相乘，所以可以利用有理数的乘法运算来进行有理数的乘方运算． 下面通过例题来熟悉有理数的乘方运算．（出示投影片§2．10 B ）［例1］计算：（1）53； （2）（－3）4； （3）（－21）3解：（1）53=5×5×5=125． （2）（－3）4=（－3）·（－3）·（－3）·（－3）=81． （3）（－21）3=（－21）·（－21）·（－21）=－81注意：（1）当底数是负数或分数时，书写时一定要先用小括号将底数括上，再在其右上角写指数．如：（－3）4不能写成－34，（－21）3不能写成－213． （2）在不会引起误解的情况下，乘号也可以用“·”表示．例如：（－3）×（－3）×（－3）×（－3）×（－3） 可写成：（－3）·（－3）·（－3）·（－3）·（－3）接下来，我们做一练习来熟悉有理数的乘方运算（出示投影片§2．10 C ）1．计算： （1）（－1）10； （2）（－1）7； （3）83； （4）（－5）3； （5）（－0．1）3；（6）［生］解：（－1）10=1； （－1）7=－1；83=512；（－5）3=－125； （－0．1）3=－0．001；（－21）4=161； 102=100；103=1000；104=10000；（－10）2=100；（－10）3=－1000； （－10）4=10000［师］很好，大家都注意了底数是负数的乘方的表示．下面我们来观察刚才练习题的结果，你能发现什么规律？可互相交流．［生］正数的任何次幂都是正数；负数的偶次幂是正数，负数的奇次幂是负数． ［师］对．大家从计算结果中，归纳出乘方运算的符号法则：（出示投影片§2．10 D ）很好．大家再想一想：0的任何次幂等于多少？1的任何次幂等于多少？以10为底数的幂有何特点？［生］由有理数的乘法可以得到：0的任何非零次幂等于0，1的任何次幂等于1． 10的几次幂，在1的后面有几个0．［师］这位同学总结得非常正确．下面，我们通过课堂练习进一步熟悉有理数乘方的概念及其运算．Ⅲ．课堂练习 课本P 73 随堂练习 1．（1）在74中，底数是_____，指数是_____．（2）在（－31）5中，底数是_____，指数是_____． 答案：（1）7，4；（2）－31，52．计算：（1）（－3）3；（2）（－1．5）2；（3）（－71）2解：（1）（－3）3=（－3）·（－3）·（－3）=－27 （2）（－1．5）2=（－1．5）·（－1．5）=2．25 （3）（－71）2=（－71）·（－71）=4913．一个数的平方为16，这个数可能是几？一个数的平方可能是零吗？答案：一个数的平方为16，这个数是4或－4．一个数的平方可能是零．0的平方是0． 4．看课本P 72～73 5．试一试设n 为正整数，计算： （1）（－1）2n ． （2）（－1）2n +1．分析：n 为正整数时，2n 表示偶数，2n +1表示是奇数．所以由乘方的符号法则，即可得出．解：（－1）2n =1 （－1）2n +1=－1 Ⅳ．课时小结本节课主要学习了有理数的乘方的意义．有关概念及其有理数乘方运算．通过本节的学习，要明确乘方和加、减、乘、除一样，是一种运算，是求n 个相同因数的乘积的运算．乘方实质是一种特殊的乘法运算．幂与和、差、积、商一样，是乘方运算的结果．乘方运算与加减乘除的运算步骤一样，先确定符号，再计算绝对值．Ⅴ．课后作业（一）课本P 74习题2．13 １、2、3．3．1米长的小棒，第一次截去一半，第二次截去剩下的一半，如此截下去，第七次后剩下的小棒有多长？解：第七次后剩下的小棒有：（21）7=21×21×21×21×21×21×21=1281（米） （二）预习内容：课本P 75．准备一张白纸．Ⅵ．活动与探究1．如果｜a +1｜+（b －2）2=0，求（a +b ）39+a 34的值．过程：让学生通过讨论、探索知道：任何一个数的绝对值是一个非负数；任何一个数的平方也是一个非负数；两个非负数的和等于0，则这两个数都为0．这样：a 、b 即可解出．结果：因为｜a +1｜+（b －2）2=0 所以a +1=0，b －2=0 即a =－1，b =2因此（a +b ）39+a 34=［（－1）+2］39+（－1）34=1+1=2． 2．用计算器补充完整下表：31 32 33 34 35 36 37 38 392781从表中你发现3的方幂的个位数有何规律？3225的个位数是什么数字？为什么？过程：让学生用计算器填完表后，认真观察，找出规律，根据规律，确定3225的个位数字．结果：31 32 33 34 35 36 37 38 39278124372921876561从表中发现3的方幂的个位数呈周期性变化，变化周期是4． 因为225=56×4+1，所以3225的个位数是3．●板书设计§2．10．1 有理数的乘方（一）一、乘方：二、例1例2●备课资料 参考练习题 1．选择题：（1）109表示（ ）A ．10个9连乘B ．10乘以9C ．9个10连乘D ．9个10连加（2）一个数的平方是正数，那么这个有理数的立方是（ ） A ．正数 B ．负数 C ．正数或负数 D ．奇数 （3）一个数的平方等于它的倒数，这个数一定是（ ）A ．0B ．1C ．－1D ．2（4）计算（－1）2000+（－1）2001÷｜－1｜的值等于（ ）A ．0B ．1C ．－1D ．1或－1（5）关于（－3）4的正确说法是（ ） A ．－3是底数，4是幂B ．－3是底数，4是指数，－81是幂C ．3是底数，4是指数，81是幂D ．－3是底数，4是指数，81是幂 答案：（1）C （2）C （3）B （4）A （5）D2．把下列各式写成乘方运算的形式，并指出底数、指数各是什么？ （1）（－1．3）·（－1．3）·（－1．3）·（－1．3） （2）51×51×51×51×51×51 答案：（1）（－1．3）（－1．3）（－1．3）（－1．3）=（－1．3）4，其中，底数是－1．3．指数是4．（2）51×51×51×51×51×51=6)51(，其中：底数是51，指数是6． 3．计算：（1）（－5）2； （2）（－43）3；（3）（－101）4； （4）5×（－51)）3．答案：（1）25 （2）－6427) （3）100001) （4）－251。

2.6有理数的乘方（1）主备人：王树山学习目标：1、理解有理数乘方的意义；2、能进行有理数的乘方运算。

课前预习：1、 填空（1） _______⨯=++222 （2）()()()()________⨯=-+-+-+-2222（3） 2222222222⨯⨯⨯⨯⨯⨯⨯⨯⨯你有什么简单的表示方法吗？（4） 2121212121212121212121⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯你有什么简单的表示方法吗？（5）n aa a a a ⨯⨯⨯⨯ 个记作___________2、 叫做乘方，乘方的结果叫做 . 在n a 中，a 叫做 , n 叫做 ,n a 读做 . 教学过程：一、展示交流：二、合作探究：例1．把下列各式写成幂的形式：（1）3333____________;⨯⨯⨯= （2）111________;222⨯⨯=（3）(3)(3)(3)(3)(3)________;-⨯-⨯-⨯-⨯-= （4）2222______.3⨯⨯⨯= 例2. 计算：（1）62 （2）3(5)- （3）4(3)-例3.计算：（1）51()2 （2）33()5 （3）42()3-讨论：（1） 3322-)(与-有什么区别？（2）223232与⎪⎭⎫ ⎝⎛有什么区别？ （3）()_________,)(______,_____,_____,=-=-===2222231931 ___________,==⎪⎭⎫ ⎝⎛-22032 （4）()_________,)(______,_____,_____,=-=-===3333331931 ___________,==⎪⎭⎫ ⎝⎛-33032 例4、手工拉面是我国的传统面食。

制作时，拉面师傅将一团和好的面，揉搓成1根长条后，手握两端用力拉长，然后将长条对折，再拉长，再对折，每次对折称为一扣，如此反复操作，连续拉扣六七次后便成了许多细细的面条。

你能计算出拉扣8次后共有多少根面条吗？那18次呢？三、质疑反馈：1. （1）在49中，底数是 ，指数是 ，49读作 ；（2）75，底数是 ，指数是 。

课题：2.10有理数的乘方【学习目标】1、能让学生在一定的现实背景中理解有理数乘方的意义；2、会熟练地进行有理数的乘方运算。

【候课朗读】有理数加法法则：⑴同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；特别地，互为相反数的两个数相加得 0 。

（3）一个数同0相加，仍得这个数有理数减法法则：减去一个数，等于加上这个数的相反数。

有理数的乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘。

任何数和0相乘，积都为 0 。

有理数除法法则：两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个非0的数都得 0。

（注意：0不能作除数）除以一个数等于乘以这个数的倒数。

【学习过程】◆学习准备1.计算2+2+2+2+2时有简便运算2.观察课本83页细胞分裂示意图，你有没有办法表示出5小时后的细胞总数:1个细胞，30分钟后变成____个，1小时后变成____个（即___×___），1.5小时后分裂成____个（即___×___×___），2小时后一共分裂了_____次，表示结果的式子______ ____=____，2．5小时后一共分裂了_____次，表示结果的式子_______ ___=____，……5小时后一共分裂了_____次，表示结果的式子________ __=____，10小时后一共分裂了_____次，表示结果的式子_____ _____=____，这是一种_____运算。

3.回想一下两个相同因数的积叫什么？如3×3=___其中__ _叫___ ，___叫___◆探究发现新知识点：知识点1 乘方：一般地，n个相同因数a相乘，记作a n，即a×a×a×…×a=a n 这种运算就是乘方，它的运算结果叫_____，a叫_____，n叫_____ a n读作_____（或______）31 ，特别地规定：一个数的1次方，就是它本身。