最新青岛版(六三制)数学小学六年级下册数学《比例的意义》重点习题1

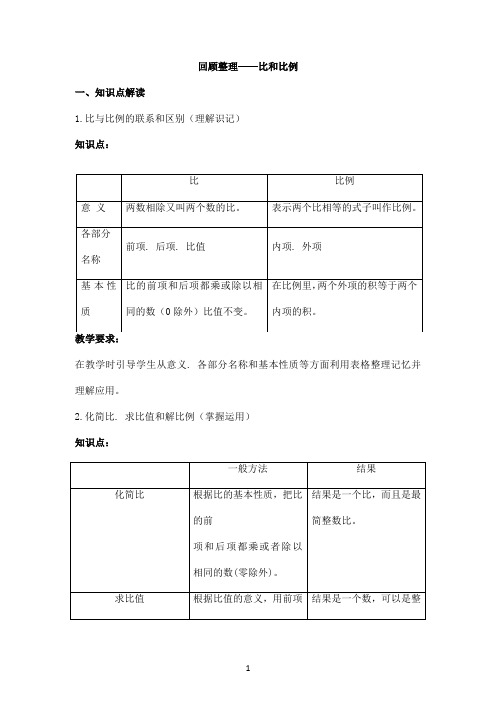
回顾整理——比和比例一、知识点解读1.比与比例的联系和区别（理解识记）知识点：在教学时引导学生从意义. 各部分名称和基本性质等方面利用表格整理记忆并理解应用。

2.化简比. 求比值和解比例（掌握运用）知识点：法以及解比例的依据和方法。

3.正比例与反比例（掌握应用）知识点：在教学时引导学生根据正比例和反比例的意义，会判断两种相关联的量是否成正比例或者反比例。

4.比例尺及比例尺应用（理解应用）知识点：要求会求相关量，即图上距离=实际距离×比例尺；实际距离=图上距离÷比例尺。

5.比、分数、除法的联系和区别（掌握应用）知识点学生在理解基础上学会灵活应用，这部分内容具有综合性，是常考点。

二、知识拓展比的应用解决按比分配问题一般方法：把比转换成分数，用分数方法解答。

先求总分数，然后求出各部分量占总量的几分之几，最后用求一个数的几分之几是多少的方法分别求出各部分量是多少。

利用正反比例解决问题一般方法：先分析数量关系，判断成什么比例，再找等量列关系式，即如果是成正比例，则按“等比”找等量列关系式；如果是成反比例，则按“等积”找等量列关系式；最后列比例式。

设未知量为X，带入等量关系式，得到正比例或反比例式，并解比例，最后写出检验和答语。

三、知识点训练基础训练1．甲. 乙两数的比是 4 ∶5，甲数是乙数的( )，乙数是甲 . 乙两数和的( )。

2．( )÷15＝（）＝( ) ∶10＝16 ∶( )＝（）%3．如果6A＝5B（A. B不为0），那么A ∶B＝( ) ∶( )。

4. 把1千克：20克化成最简整数比是（），他们的比值是（）。

5. A、B两地实际距离是180 km，在地图上的距离是3 cm，这幅地图的比例尺是( )。

能力提升1. 一幅精密零件的图纸，比例尺是80 ∶1，则图上距离是实际距离的( )，实际距离是图上距离的( ）2. 一种盐水中，盐的质量是水的25%。

现有5克盐，要配制这种盐水，需要加入多少克水？1.一种盐水，盐与水的质量比是1∶4。

青岛版小学数学六三制
六年级下册
好的开始，是成功的一半，祝您天天进步！
来一起学习知识吧
《比例的意义》综合习题
1、填一填。

（1）表示两个（ ）相等的式子叫比例。

（2）组成比例的四个数，叫作比例的（ ）。

两端的两项叫作比例的（ ），中间的两项叫作比例的（ ）。

2、
（1）甲、乙两个正方形边长的比是（ ），比值是（ ）。

（2）甲、乙两个正方形周长的比是（ ），比值是（ ）。

（3）甲、乙两个正方形面积的比是（ ），比值是（ ）。

（4）上面的三个比中，（ ）和（ ）的比值相等，所以可以组成比例式为（ ）。

3、判断下面每组的两个比是否可以组成比例。

（1）0.4：8与 8：16 （2）与3：4 :1134
4、（1）4的因数有（ ），从中挑选4个数组成比例是（ ）。

（2）4、6、16、24可以组成比例，则比例可以写为4：（ ）＝16：（ ）或24：（ ）＝16：（ ）。

（3）用20以内的两个质数和两个合数组成一个比例：（ ）。

5、下面是某酒厂啤酒生产情况记录表。

（1）任意写出3组相对应的工作总量与工作时间的比，求出比值并比较大小。

（2）这个比值所表示的意义是（）。

（3）表中的数据能组成比例吗？为什么？请写出两个比例式。

6、如图，工人师傅用两块同样长的木板搭两个斜坡。

（1）分别写出斜坡①②最高点的高度与木板的长度的比，并写出比值。

（2）比较两个比值的大小，你发现了什么？。

新青岛版六年级下数学（课课练）第4单元第1课时比例尺的意义一、填空。

1. 比例尺1︰800，它表示实际距离是图上距离的（）倍。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】8002. 实际距离是图上距离的50000倍，这幅图的比例是（）。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】1：500003. 如果一幅图上的1厘米距离，表示实际距离是300米，那么这张图的比例是（）或写成（）。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】1:30000 或1/300004. 一张图纸的比例是200：1，图上距离和实际距离（）大。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】图上距离5. 甲乙两城相距720千米，在一幅地图上量行两城相距12厘米，这幅图的比例尺是（）。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】1:60000006. （）和（）的比叫做这幅图的比例尺。

比例尺分为（）比例尺和（）比例尺。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】图上距离实际距离数值线段7. 在比例尺是1：4000000的地图上，图上距离1厘米表示实际距离（）千米。

也就是图上距离是实际距离的（），实际距离是图上距离的（）倍。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】40 1/4000000 40000008. 在一幅比例尺是30 ：1的图纸上，一个零件的图上长度是12厘米，它的实际长度是（）。

【解析】图上距离和实际距离的比，叫做这幅图的比例尺。

【答案】0.4厘米二、判断。

1. 在一幅地图上量得5厘米的距离表示实际400米的距离，这幅地图的比例尺是1︰80。

（）【解析】考察比例尺的定义，以及单位的换算。

【答案】×2. 如果一幅图的图上距离等于实际距离，那么这幅图的比例是1︰1。

（）【解析】考察比例尺的定义，以及单位的换算。

学科数学年级六教师单位姓名课题正比例的意义1 二次修改教学目标1.经历概括两种量成正比例关系的过程。

2.理解正比例的意义，能根据正比例的意义正确判断两种量是否成正比例关系。

3.增强探索知识和规律的意识，养成积极主动参与学习的习惯。

学生交流。

如工作时间扩大2倍，教学重点理解正比例的意义，能根据正比例的意义正确判断两种量是否成正比例关系。

教学难点理解正比例的意义，能根据正比例的意义正确判断两种量是否成正比例关系。

教学过程一、创设情境、激趣导入。

师：同学们，青岛啤酒是我们青岛的名牌产品，每年的啤酒节都能吸引海内外的许多宾朋。

今天我们一起到啤酒生产车间去参观一下。

出示表格。

工作时间（时）1 2 3 4 5 6 7 …工作总量（吨）14 28 42 56 70 84 98 …师：仔细观察统计表，说说你了解到的数学信息。

二、探索尝试，解释交流。

1.师：观察上面的记录表，你有什么发现？师：对，工作时间越长生产的啤酒越多，工作时间越短生产的啤酒越少。

师：工作总量和工作时间是有联系的两个数量。

那么工作总量和工作时间是怎样变化的？2.师：请大家计算它们的比值，看又有你有什么发现？师：这个比值实际上是什么？你能用一个式子表示它们的关系吗？3.师：通过观察发现，工作时间变化，工作总量也随着变化，且工作总量与工作时间的比值一定，我们就说工作总量和工作时间是成正比例的量，它们的关系叫做正比例关系。

4.师：生活中还有许多这样成正比例关系的量，我们来看看神州五号飞太空飞行的情况记录。

（自主练习第一题师：观察表格里的信息，独立思考下面的问题，再和同位交流。

1.表中（）和（）是相关联的量。

2.任意写出三个相对应的路程和时间的比，并算出它们的比值。

3.比值实际上表示（），并用式子表示它们的关系。

三、拓宽应用。

1.自主练习第2题。

2.判断下面的两种量是否成正比例，并说明理由。

1）长方体的高一定，体积和底面积。

2）和一定，一个加数和另一个加数。

新青岛版六年级下数学（课课练）第3单元第4课时正比例的意义一、判断。

1．一个因数不变，积与另一个因数成正比例。

（）2．长方形的长一定，宽和面积成正比例。

（）3．大米的总量一定，吃掉的和剩下的成正比例。

（）4．圆的半径和周长成正比例。

（）5．分数的分子一定，分数值和分母成正比例。

（）6．铺地面积一定，方砖的边长和所需块数成正比例。

（）7．圆的周长和直径成正比例。

（）8．除数一定，被除数和商成正比例。

（）9．和一定，加数和另一个加数成正比例。

（）解析：本题考查学生对正比例关系的理解，注意必须有两个关联量，比值一定，这两个量才是正比例关系。

答案：一、1. √ 2. √ 3. × 4. √ 5. × 6. × 7. √ 8. √ 9. ×二、填空。

1．两种（）的量，一种量变化，另一种量（），如果这两种量中（）的两个数的（）一定，这两种量就叫做成正比例的量，它们的关系叫做（），关系式是（）。

2．一房间铺地面积和用砖数如下表，根据要求填空。

（1）表中（）和（）是相关联的量，（）随着（）的变化而变化。

（2）表中第三组这两种量相对应的两个数的比是（），比值是（）；第五组这两种量相对应的两个数的比是（），比值是（）。

（3）上面所求出的比值所表示的的意义是（），铺地面积和砖的块数的（）是一定的，所以铺地面积和砖的块数（）。

3．练习本总价和练习本本数的比值是（）。

当（）一定时，（）和（）成（）比例。

解析：考查正比例关系的定义和运用。

答案：二、1. 相关联也随着变化相对应比值（商）2. （1）铺底面积用砖块数用砖块数铺底面积（3）铺地面1平方米所需砖的块数为25 比值成正比例关系3. 练习本单价练习本单价练习本总价练习本本数正三、说说下面的每题中的两种量是不是成正比例，并说明理由。

（1）每袋大米的质量一定，大米的总质量和袋数。

（2）东东和爸爸的年龄。

（3）一本书，已经看的页数和还没看的页数。

第三单元《快乐足球—比例》单元框架信息窗1——比例的意义和性质一、知识点解读1.比例的意义（理解识记）知识点：表示两个比相等的式子叫做比例。

如∶（3∶4=9∶12）。

比例有四个项，分别是两个内项和两个外项。

在3∶4=9∶12中，其中3与12叫做比例的外项，4与9叫做比例的内项。

比例的四个数均不能为0。

教学要求：要联系比的意义来理解比例的意义。

“比是表示两个数相除，有两个数；比例是一个等式，表示两个比相等，有四个数。

”2.比例的基本性质（掌握运用）知识点：在一个比例中，两个外项的积等于两个内项的积。

教学要求：通过举例的方式多找几个比例试一试，看看它们是不是也有这样的规律？然后再运用比例的基本性质判断两个比是否能组成比例。

例如0.4∶25能否和1.2∶75组成比例？为什么？因为0.4×75＝25×1.2，所以0.4∶25和1.2∶75能组成比例。

3.解比例（掌握运用）知识点：根据比例的基本性质，如果已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。

求比例中得未知项，叫做解比例。

教学要求：解比例可以根据比例的基本性质把比例转化成方程，然后用解方程的方法求出未知数X 。

二、知识拓展解形如b a =dc形式的比例（分数形式的比例）。

方法：解形如b a =dc形式的比例时，根据等号两端的分子和分母交叉相乘，乘积相等，将比例化成与积有关的方程，再通过解方程求出未知项的值。

例如:54=x 9。

解: 4x=45，x=445 三、知识点训练基础训练1. 下面哪一组中的两个比可以组成比例，并写出相应的比例。

7∶14和6∶12 3.5∶7和1∶14 0.4∶1.6和3∶122. 解比例。

10∶50＝x ∶40 1.3∶x ＝5.2∶203. 根据题意，先写出比例式，然后解比例。

(1)8与x 的比等于4与32的比。

(2) 0.5与y 的比值就是0.25∶4的比值。

能力提升1. 如果5a=3b ，那么b a = （ ）， ab =（ ）。