线性定常系统的状态空间分析与综合

第十章 线性系统的状态空间分析与综合10-1 求通过1)0(=x ，2)1(=x ，使下列性能指标为极值的曲线：⎰+=ft t t d xJ 0)1(2 。

解：12+=xL ；0=∂∂x L ，x x L 2=∂∂，x xLt d d 2=∂∂； 欧拉方程为 0=x；通解为 b t a t x +=)(； 所求极值曲线为 1)(+=t t x ，)2(=*J 。

10-2 设)(t x x =，10≤≤t ，求从0)0(=x 到1)1(=x 间的最短曲线。

解：2/122)(t d x d s d +=，⎰⎰+==12/120)1(1t d xs d J s ； 2/12)1(+=xL ；0=∂∂xL，2/12)1(-+=∂∂x x x L ； 欧拉方程为 0=∂∂-∂∂x L t d d x L ，0)1(2/12=+xxt d d ；要求 a x = 为常数，即t a t x =)(； 所求极值曲线为 t t x =)(，)2(=*J 。

10-3 求性能指标⎰+=12)1(t d xJ 在边界条件0)0(=x ，)1(x 是自由情况下的极值曲线。

解：极值曲线需满足欧拉方程、边界条件和横截条件；0=∂∂-∂∂x Lt d d x L ；)1(0)0(x x =；0),,()(T=+⎪⎪⎭⎫ ⎝⎛∂∂**f tf t t t xx L t x x L ffδδ ； 12+=xL ；0=∂∂x L ；x x L 2=∂∂，x xLt d d 2=∂∂； 0=∂∂ft xL，0=x；即c t x =)(； 考虑边界条件，所求极值曲线为 0)(=t x ， )1(=*J 。

注：直观)1(2+x取最小值，即要求0=x ，满足)1(x 自由。

10-4 求性能指标⎰++=2/0212221)2(πt d x x x x J在边界条件0)0()0(21==x x ，1)2/()2/(21==ππx x 情况下的极值曲线。

第5章线性定常系统的综合5.1 系统综合的概念1、系统综合系统综合：确定系统控制规律（控制器的结构和参数）。

控制方式：开环/闭环（反馈）控制。

反馈控制综合方法：时域法（状态空间法），复频域法（根轨迹法、对数频率特性法等）。

2、期望极点系统的动态性能与闭环极点和零点都有关，但主要地取决于极点在左半s平面上的位置。

根据系统时域性能指标所确定的综合后系统的极点称为期望闭环极点。

通过系统综合使闭环系统极点分布在期望位置称为极点配置。

◆典型二阶系统222()2nn nG s s s ωζωω=++ 当给定系统的p M 和s t (2%~5%)∆=，可确定系统的期望闭环主导极点为*21,2j j 1d n n λσωζωωζ=±=-±-式中，p M 为最大超调量，s t 为调节时间，ζ为阻尼比，n ω为自然振荡频率。

()y t t2∆st p t r t 1maxy pM⨯⨯ImRe01ζ<<*1,2j dλσω=±dωnωσθ◆单变量高阶系统以将闭环系统设计为近似二阶系统的目标，先按照系统的p M 和s t 确定闭环主导极点为*1,2j d λσω=±，再按照*1,2Re[]5Re[]i λλ>的要求确定其他期望闭环极点*(3,4,,)ii n λ=。

若原系统在期望闭环主导极点附近有零点，可有意设置期望极点与其形成偶极子，以保证闭环主导极点的主导性。

ReIm⨯⨯σ5σ⨯⨯⨯⨯⨯闭环主导极点*1,2j dλσω=±◆多变量系统确定期望极点的难度较大。

一般先分别确定各子系统的期望极点，再进行协调。

3、综合的内容动态+稳态5.2 两种比例反馈（取自讲义5.2/5.3）1、输出比例反馈和状态比例反馈对系统0(,,)S A B C ▼输出比例反馈⊗vB⊗⎰ACFyxux图中，r m F ⨯—输出反馈系数矩阵；1r v ⨯—参考输入。

原系统的控制量成为u Fy v =+即u FCx v =+闭环系统(,,)f f S A B C 为()BF x A x C v B =++y Cx =▼状态比例反馈⊗vB⊗⎰ACKyxux图中，r n K ⨯—状态反馈系数矩阵；1r v ⨯—参考输入。

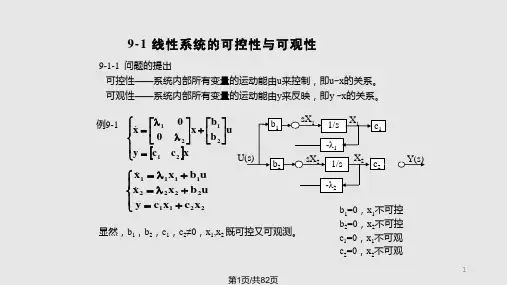
第九章线性系统的状态空间分析法一、教学目的和要求通过学习，了解系统状态空间描述常用的基本概念，掌握线性定常系统状态空间表达式的建立方法。

二、重点状态空间分析的常用概念，根据系统机理建立状态空间表达式方法。

三、教学内容：以“经典控制的不足”为切入点引进线性系统的状态空间分析与综合。

1、系统数学描述的两种基本方法一种是外部描述。

一种是内部描述。

对比举例2、系统描述中常用的基本概念输入和输出、松弛性、因果性、线性、时不变形3、系统状态空间描述常用的基本概念状态和状态变量、状态向量、状态空间、状态轨迹、状态方程、输出方程、状态空间表达式、自制系统、线性系统、线性系统的状态空间表达式、线性定常系统、线性系统的结构图、状态空间分析法。

将概念讲解、举例、对比来加深理解。

4、举例熟悉对概念理解5、根据系统机理建立状态空间表达式方法步骤：①确定输入输出向量；②根据系统机理（电学、力学等）建立系统方程；③选择状态变量，根据方程建立状态方程；④列写输出方程；⑤将状态方程、输出方程变换为向量—矩阵形式。

举例：RLC网络（单输入-单输出）；机械位移系统（双输入-三输出）第一节 线性系统的状态空间描述一、教学目的和要求掌握线性定常系统状态空间表达式的建立方法。

二、重点由传递函数建立状态空间表达式 三、教学内容：1、由系统微分方程建立状态空间表达式方法（单输入-单输出） （1）系统输入量中不含倒数项。

()(1)(2)12100...n n n n n y a y a y a y a y uβ∙----+++++=式中y ,u 分别为系统的输出、输入量；0110,,...,,n a a a β-是由系统特性确定的常数。

由于给定n 个初值1(0),(0),...(0)yn y y - 及t ≧0的u （t ）时，可唯一确定t>0时系统得的行为，可选取n 个状态变量为(1),,...,12n x y x y x y n -===，故上式可化为12231 (011210)x xx xxx nn x a x a x a x un n n y xβ∙∙∙∙∙∙∙===-=----+-=再将上式写成向量-矩阵形式，并画出状态变量图。