线性系统的状态空间描述

格式：docx
大小：112.77 KB
文档页数：19

下载文档原格式

线性系统的状态空间描述

第一章线性系统的状态空间描述 1. 内容系统的状态空间描述化输入－输出描述为状态空间描述由状态空间描述导出传递函数矩阵线性系统的坐标转换组合系统的状态空间方程与传递函数矩阵2. 基本概念系统的状态和状态变量状态：完全描述系统时域行为的一个最小变量组。

状态变量：构成系统状态的变量。

状态向量设系统状态变量为)(,),(),(21t x t x t x n 写成向量形式称为状态向量，记为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()()(21t x t x t x t x n状态空间状态空间：以状态变量为坐标轴构成的n 维空间。

状态轨迹：状态变量随时间推移而变化，在状态空间中形成的一条轨迹。

3. 状态空间表达式设系统r 个输入变量：)(,),(),(21t u t u t u r m 个输出：)(,),(),(21t y t y t y m n 个状态变量：)(,),(),(21t x t x t x n例：图示RLC 电路，建立状态空间描述。

电容C 和电感L 两个独立储能元件，有两个状态变量，如图中所注，方程为)()()()()()(t i dtt du C t u t u t Ri dtt di LL c c L L ==++ )()(),()(21t u t x t i t x c L ==状态方程)(01)()(0/1/1/)()()()()()()()(212112211t u t x t x C L L R t xt x t x t xC t u t x t Rx t x L ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⇔⎩⎨⎧==++⇔输出方程[]⎥⎦⎤⎢⎣⎡==)()(01)()(21t x t x t u t y c 一般定义状态方程：状态变量与输入变量之间的关系[][][]t t u t u t u t x t x t x f t xdt t dx t t u t u t u t x t x t x f t xdt t dx t t u t u t u t x t x t x f t xdt t dx r n n n n r n r n );(,),(),();(,),(),()()();(,),(),();(,),(),()()();(,),(),();(,),(),()()(212121212222121111======用向量表示，得到一阶的向量微分方程[]t t u t x f t x),(),()(= 其中n n r r n n f f f f t u t u t u t u t x t x t x t x R R R ∈⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∙∙∙=∙∈⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=∈⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()(:)(,)()()(:)(,)()()(:)(212121输出方程：系统输出变量与状态变量、输入变量之间的关系，即[][][]t t u t u t u t x t x t x g t y t t u t u t u t x t x t x g t y t t u t u t u t x t x t x g t y r n m m r n r n );(,),(),();(,),(),()();(,),(),();(,),(),()();(,),(),();(,),(),()(2121212122212111=== 用向量表示为[]t t u t x g t y ),(),()(=4系统分类：1) 非线性时变系统[][]⎩⎨⎧==t t u t x g t y t t u t x f t x ),(),()(),(),()(2) 非线性定常系统[][]⎩⎨⎧==)(),()()(),()(t u t x g t y t u t x f t x3) 线性时变系统⎪⎩⎪⎨⎧+++++=+++++=rnr n n nn n n r r n n u t b u t b x t a x t a xu t b u t b x t a x t a x)()()()()()()()(1111111111111写成向量形式即为⎩⎨⎧+=+=)()()()()()()()()()(t u t D t x t C t y t u t B t x t A t x其中：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()()()()()()()()(,)()()()()()()()()()(212222111211212222111211t b t b t b t b t b t b t b t b t b t B t a t a t a t a t a t a t a t a t a t A nr n n r r nn n n n n ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)()()()()()()()()()(,)()()()()()()()()()(212222111211212222111211t d t d t d t d t d t d t d t d t d t D t c t c t c t c t c t c t c t c t c t C mr m m r r mn m m n n4) 线性定常系统⎩⎨⎧+=+=)()()()()()(t Du t Cx t y t Bu t Ax t x5 状态空间表达式的系统结构图状态和输出方程可以用结构图表示，形象地表明系统中信号传递关系。

第22 线性系统的状态空间描述

其中 A(t) n×n — 系统矩阵 B(t) n×r — 输入矩阵 C(t) m×n — 输出矩阵 D(t) m×r — 前馈矩阵
D(t)
X
X
U
B(t)
C(t)
Y
A(t)
离散时间线性系统的状态空间描述
离散系统：各变量在离散时刻取值，状态空间反映离散时刻的变量组间的因果关系和变换关系。用 k=0,1,2…表示离散时刻。状态空间描述形式：
的因果关系，即输入和输出间的因果关系。例如：线性定常、单输入－单输出系统，外部描述为线性常系
数微分方程。
y(t) an1 y(n1) (t) a1 y(t) a0 y(t) bm u(m) (t) bn1u(m1) (t ) b1u(t ) b0u(t )
零初始条件下，传递函数为：
输出方程／量测方程：代数方程
y1 g1 ( x1, , xn ; u1, , ur ; t)
t t0
ym gm ( x1, , xn ; u1, , ur ; t)
向量形式：
y g(x, u, t)
• 线性系统的状态空间描述
x A(t)x B(t)u
y
C(t)
x
D(t
)u
t t0
L diL dt
L diL dt
0 e
e(t)
R1
C
iC
L
iL U c R2 U R2
uc
iL
(R1
1
R2 R1
)C
L(R1 R2 )
(
R1
R1 R2 R1R2
)C
uc
iL
(
R1
1
R2 R2
)C
e

第1章线性系统的状态空间描述

x&(t) Ax(t) Bu(t) y(t) Cx(t) Du(t)
• 情况1：输入u不含导数
y(n) an1y(n1) L a1y& a0 y bu
自主技术与智能控制研究中心
二、状态空间模型的建立
输入u不含导数 y(n) an1y(n1) L a1y& a0 y bu
选取状态变量 x1 y x2 y x3 y
I ml2 ml
自主技术与智能控制研究中心
ml M m
二、状态空间模型的建立
用一阶微分方程组表示系统模型！
&x& 1m2l2 g 1(I ml2 )u && 1(M m)mgl 1mlu
引入新的变量
x1 x x2 x&
x3 x4 &
x&1 x2
x&2 x&3
{1m2l x4
x&% Ax% Bu%
y%
Cx%
Du%
f1
A
f x
|x0
,u0
x1
M
fn x1
L O L
f1 xn
M
fn xn
B
f u
|x0 ,u0
,C
g x
|x0
,u0
,
D
g u
|x0 ,u0
自主技术与智能控制研究中心
二、状态空间模型的建立例3：质量-弹簧-阻力器系统
自主技术与智能控制研究中心
u
线性化 0 V mg
m
d2 dt 2
(x
l
sin )
H
I&& Vl Hl
m d 2 (l cos) V mg

1线性系统的状态空间描述

数学表达式(具有代数方程形式),称输出方程. 二. 状态和状态空间 1. 状态和状态向量状态——是指系统的时域行为或运动状态.定义为完全表征系统时间域行为的一个最小内部变量组. 状态变量——是指能够完全描述系统时域行为的一个最小变量组中的每个变量. 状态向量——由状态变量构成的列向量称状态向量. 如某组状态变量有n个状态变量x1(t),x2(t),…,xn(t) (t>=t0) 则状态向量为:
n ×1
b 11 ( t ), L , b 1 p ( t ) B (t ) = M b ( t ), L , b ( t ) np n1 n× p d 11 ( t ), L , d 1 p ( t ) D (t ) = M d ( t ), L , d ( t ) qp q1 q× p
x ( k + 1 ) = f ( x ( k ), u ( k ), k ) y ( k ) = g ( x ( k ), u ( k ), k ) k = 0 ,1 , 2 L
x ( k + 1) = G ( k ) x ( k ) + H ( k )u ( k ) 线性离散系统: y ( k ) = C ( k ) x ( k ) + D ( k )u ( k )
u(t)—输入标量函数; y(t)—输出标量函数; d(t)—标量函数,称直接传递系数. 2 多输入多输出时变系统的状态空间模型
& X (t ) = A (t ) x (t ) + B (t )u (t ) y (t ) = C (t ) x (t ) + D (t )u (t )
式中:
X ( t ) = [x 1 ( t ), x 2 ( t ), L , x n ( t ) ]T a 11 ( t ) L a 1 n ( t ) A (t ) = M a (t ) L a (t ) nn n1 n× n c 11 ( t ), L , c 1 n ( t ) C (t ) = M c q 1 ( t ), L , c qn ( t )

线性系统理论第2章线性系统的状态空间描述

D(k )
u(k )
H (k )

x(k 1)

x(k )
单位延迟

C (k )

y(k )
G (k )
7/7,11/50
2.3.连续变量动态系统按状态空间描述的分类
线性系统和非线性系统
设系统的状态空间描述为 x f ( x, u, t ) y g ( x, u, t )
向量函数
g1 ( x, u, t ) f1 ( x, u, t ) g ( x, u , t ) f ( x, u , t ) ，g ( x, u, t ) 2 f ( x, u , t ) 2 g q ( x, u , t ) f n ( x, u , t )
和t≥t0 各时刻的任意输入变量组 u1 (t ),u2 t ,, u p (t ) 那么系统的任何一个内部变量在t≥t0各时刻的运动行为也就随之而完全确定
3/4,3/50
(2).状态变量组最小性的物理特征：少一个不行，多一个没用 (3). 状态变量组最小性的数学特征：极大线性无关变量组 (4). 状态变量组的不唯一性：任意
1/18,14/50
结论1
给定单输入,单输出线性时不变系统的输入输出描述,
y ( n) an1 y ( n1) a1 y (1) a0 y bmu ( m) bm1u ( m1) b1u (1) b0u
Y (s) bm s m bm1 s m1 b1 s1 b0 g ( s) U ( s) s n an1 s n1 a1 s a0
时变系统和时不变系统
f f ( x, u ) 若向量f,g不显含时间变量t,即 g g ( x, u )

现代控制工程-第二章线性系统的状态空间描述

1 x3 s

1 s

1 x1 s
y(t )
2
3
8 64
解：第一步：化简方框图，使得整个系统只有标准积分器（1/s）、比例器（k）及加法器组成。第二步：将上述调整过的结构图中的每个标准积分器（1/s）的输出作为一个独立的状态变量xi，积分器的输入端就是状态变量的一阶导数dxi/dt。第三步：写出每个状态变量的一阶微分方程，从而写出系统的状态方程。
y Cx Du
图2－2 系统动态方程的方块图结构
状态空间分析法具有下列优越之处：
便于在数字计算机上求解；
容易考虑初始条件；能了解并利用处于系统内部的状态信息；数学描述简化；
适于描述多输入－多输出、时变、非线性、随机、离散等各类系统，是最优控制、最优估计、辨识、自适应控制等现代控制系统的基本描述方法。
例2.2.3求如图所示系统的动态方程。
（a）系统方块图
u(t )

s 1 s2
1 s3
1 s 2 8s 64
y(t )
（b）第一次等效变换

1 s3

u(t )

1 s2

1 s( s 8)
y(t )
64
（c）由标准积分器组成的等效方块图
u(t )

1 x4 s

(2-5)
y t cx t du(t )
，cn ，d为直接联系输入量、输出量其中 c c1，c2，的前向传递（前馈）系数，又称前馈系数。
多输入－多输出（含q个输出变量）线性定常连续系统的输出方程一般表达形式为：
y1 c11 x1 c1n xn d11u1 d1 pu p yq cq1 x1 cqn xn d q1u1 d qp u p

第2章线性系统的状态空间描述

特征多项式定义2.4 [特征矩阵] 特征矩阵] 定义
定义2.5 [特征多项式] 特征多项式] 定义
2.4 线性时不变系统的特征结构
特征多项式α(s)的计算方法的特征多项式
莱弗勒(Leverrier)递推算法递推算法莱弗勒
2.4 线性时不变系统的特征结构
α ( s ) = s n + α n −1s n −1 + L + α1s + α 0
0 1 0 A = 0 0 1 0 −1 −1
5，化下列各状态方程为对角线规范型或约当规范型化下列各状态方程为对角线规范型或约当规范型
8 −8 −2 2 3 & x = 4 −3 −2 x + 1 5 u 3 −4 1 7 1
0 1 4 & x= x + 2 u −9 −6
作业
6，计算下列状态空间描述的传递函数计算下列状态空间描述的传递函数 −5 −1 2 & x= x + 5 u 3 −1 y = [1 2] x + 4u 7，给定反馈系统如下图所示给定反馈系统如下图所示
& 为 x1 = y , x2 = y ，列出系统的状态方程和输
出方程
u
+ −
&& y
+
∫
by 2
& y
二次部件
∫
y
+ + +
a (t )
k
作业
2，试求出下列各个输入输出描述的一个状态空间描述试求出下列各个输入输出描述的一个状态空间描述
&&& + 2&& + 6 y + 3y = 5u y y & &&& + 2&& + 6 y + 3 y = 7u + 5u & y y & & & 3&&& + 6 && + 12 y + 9 y = 6u + 3u y y

第2章线性系统的状态空间描述

t1
(t
t1
)dt
1
（2）对任何在 t1时刻连续的函数f(t),有
f (t) (t t1)dt f (t1)
12
第2章线性系统的状态空间描述
➢非零初始条件与等价的脉冲输入结论：非零初始条件对应的系统响应
等效于在初始时刻脉冲输入时的系统响应。以后在建立系统的输入—输出描述
时，均假定系统的初始条件为零。
u p1
System
yq1
视系统为 black box
5
第2章线性系统的状态空间描述
例如：
从输入—输出关系来看，它们具有相同的传递函数：
G(s) 1 s 1
实际上这两个系统是不等价的，一个是能观不能控的，一个是能控不能观的。
表明:系统的内部特性比起由传递函数表达的外部特性要复杂得多，输入—输出描述没有包含系统的全部信息，不能完整的描述一个系统。
或
x(k 1) y(k) g
f [
[ x(k x(k ),
), u(k), k u(k), k ]
]
24
第2章线性系统的状态空间描述
(4)．线性系统状态空间表达式：状态方程与输出方程都是线性方程的系统是线性系统。线性系统的状态方程是一阶向量线性微分方程或一阶向量线性差分方程。
1 非零初始条件与脉冲输入
➢ 系统的初始条件为零是指系统在初始时刻没有能量储备，系统输出只由此后的输入唯一地确定。
➢ 在建立线性系统的输入—输出描述时，必须假设系统的初始条件为零。
初始条件不为零时如何处理？
➢ 初始条件不为零时，可以将非零的初始条件等效成在初始时刻的一个脉冲输入。
10
第2章线性系统的状态空间描述

2线性系统的状态空间描述

C m ia J
dt
2
f
转动惯量，粘性摩擦常数， m 电磁转矩常数，e 电势常数 C C f
令 x1 , x 2 , x 3 i a
x1 x 2 x2 x3 f J Ce La x2 x2 Cm J Ra La x3 x3 u La
结构图
x2
状态轨迹
A
( x1 ( t 0 ), x 2 ( t 0 ))( x1源自( t1 ), x 2 ( t1 ))
B
0
x1 ( t ) x (t ) x 2 (t )
t
x1
状态空间分析法举例
例1求图示机械系统的状态空间表达式
外力 u ( t )
K ---弹性系数 m
7.状态空间表达式(动态方程)：{A，B，C，D}
x f ( x, u , t) y (t ) g ( x , u , t )
x ( t k 1 ) f ( x , u , t k ) y (tk ) g ( x , u , tk )
f,g-线性函数线性系统
u
y 1
0
例4. 一长度为l ，质量为m的单倒立摆，用铰链安装在质量为M的小车上，小车受电机操纵，，在水平方向施加控制力u，相对参考坐标系产生位移x。要求建立该系统的状态空间表达式。

m
x
l
u
M
设小车瞬时位置为 x 摆心瞬时位置为 ( x l s i n ) 在水平方向，由牛顿第二定律
yq
u [u1 , u 2 , , u p ]
T
y [ y1 , y 2 , , y q ]

第二章线性系统的状态空间描述1

第二章线性系统的状态空间描述§2-1 状态空间的基本概念1、状态：系统的状态，是指系统的过去、现在和将来的状况。

（如：一个质点作直线运动，它的状态就是它每个时刻的位置和速度）2、状态变量：能完全表征系统运行状态的最小数目的一组变量。

（如果用最少的n 个变量x 1(t)， x 2(t)，……， x n (t)就能完全描述系统的状态，那么这n 个变量就是一组状态变量。

）3、状态向量：设一个系统有n 个状态变量，即x 1(t)，x 2(t)，……，x n (t)，用这n 个状态变量作为分量构成的向量x(t)称为该系统的状态向量。

记为Tn t x t x t x t x )](,),(),([)(21 =4、状态空间：由n 个状态变量作为坐标轴所构成的n 维空间，称为状态空间。

引入了状态和状态空间的概念之后，就可以建立动力学系统的状态空间描述了。

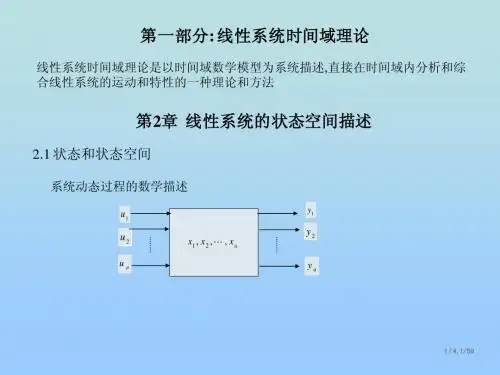
从结构的角度讲，一个动力学系统可用图2-1所示的方块图来表示。

其中x(t)表征系统的状态变量，u(t)为系统控制量（即输入量），y(t)为系统的输出变量。

与输入—输出描述不同，状态空间描述把系统动态过程的描述考虑为一个更为细致的过程：输入引起系统状态的变化，而状态和输入则决定了输出的变化。

5、状态方程：状态变量的一阶导数与状态变量、输入量的关系，称为系统的状态方程。

例：设单输入线性定常系统(LTI-Linear Time Invariant )的状态变量为x 1(t)，x 2(t)，……，x n (t)，输入为u(t),则一般形式的状态方程为：)()()()()()()()()()()()()()()()()()()()()(2211222221212112121111t u b t x t a t x t a t x a t x t u b t x t a t x t a t x a t x t u b t x t a t x t a t x a t x n n nn n n nn n n n ++++='++++='++++='图2-1 动力学系统结构示意图上式可写成向量—矩阵形式：其中：6、输出方程：在指定系统输出的情况下，该输出与状态变量、输入量之间的函数关系式，称为系统的输出方程。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章线性系统的状态空间描述1.内容系统的状态空间描述化输入—输出描述为状态空间描述由状态空间描述导出传递函数矩阵线性系统的坐标转换组合系统的状态空间方程与传递函数矩阵2.基本概念系统的状态和状态变量状态：完全描述系统时域行为的一个最小变量组状态变量：构成系统状态的变量状态向量设系统状态变量为X i(t),X2(t)厂，X n(t)写成向量形式称为状态向量，记为_X i(t)x(t)=_X n(t)状态空间状态空间：以状态变量为坐标轴构成的n维空间状态轨迹：状态变量随时间推移而变化，在状态空间中形成的一条轨迹。

3. 状态空间表达式设系统r 个输入变量：U i (t ),u 2(t )^ ,u r (t )m 个输出：yQM), ,y m (t)n 个状态变量：X i (t),X 2(t), ,X n (t)例：图示RLC 电路，建立状态空间描述i LC电容C 和电感L 两个独立储能元件，有两个状态变量, 方程为如图中所注,Ldi L (t)dtRi L (t) U c (t) =u(t)C 沁 “L (t)dtX i (t)二 L(t), X 2(t)二 U c (t)二 LX i (t) RX i (t) X 2(t)二 u(t)Cx (t)二 X (t) N(t) - R/L 殳⑴门1/C0 匚X 2(— Ou(t)U c输出方程一般定义状态方程：状态变量与输入变量之间的关系dX i (t) dt = X i (t)二 f i 〔X i (t),X 2(t), ,X n (t)；U i (t),U 2(t), ,U r (t);tl dX 2(t) dt = X 2(t)二 f 2'X i (t),X 2(t)^ ,X n (t)；U i (t),U 2(t), ,U r (t)；t 】dX n (t) dt 二 X n (t)二 f n 〔X i (t),X 2(t), ^⑴小⑴心⑴,,U 「(t)；t 】用向量表示，得到一阶的向量微分方程x(t)二 f 'X(t),u(t), t 1其中X i (t)U ](t)fQ) “、 X 2(t) -U 2(t) .f 2(・)・QnX(t) -c R ,u(t)戶；cR , f (•) ^^： cR N(t) 一JU r (t) 一-f n (叽输出方程：系统输出变量与状态变量、输入变量之间的关系，即%(t)二 g i X i (t),X 2(t),,X n (t)；U i (t),U 2(t), ,U r (t)；t ]y 2(t)二 g 2 X i (t), X 2(t), ,X n (t)；U i (t),U 2(t),,U r (t)；t 〔y(t)二％(t)二 101 X i (t) 殳(t).y m(t)二g m X i(t),X2(t), ,X n(t)；U i(t),U2(t),,U r(t)；t】用向量表示为y(t)二gX(t),U(t),t]4系统分类：1) 非线性时变系统：x(t) = f〔x(t),u(t),t 】y(t)二 g〔x(t),u(t),t 〕2) 非线性定常系统x(t)二 f 〔x(t),u(t)】 y(t)二 g'x(t),u(t)]3) 线性时变系统‘X i =a“(t)X i + …+a in (t)X n +bn(t)u i + …+匕「住)山 jX n =a ni (t)X i + …+a nn (t)X n +b ni (t)U i + …+0「住)山写成向量形式即为：x(t) = A(t)x(t)+B(t)u(t) y(t)=C(t)x(t) + D(t)u(t)其中：4) 线性定常系统a ii (t) a i2(t)a 2i (t) a 22 (t) A(t)—: :a in (t) bn(t)b i2 (t) a2n ⑴，B(t)=b ⑴ b22(t) _a ni (t)a n2(t) a nn (t) 「Gi(t)C(t)二C 2i (t) cmi (t )G2(t) C 22(t )a_b ni (t) b n2(t)C in (t)〕"dn(t) d i2(t)C 2n (t) d 2i (t) d 22(t)，D(t)=Cmn(t)_-dmi(t)dm2(t)d ir (t) d 2r (t )b ir (t) b 2r (t)ab nr (t)「x(t) = Ax(t) + Bu(t)y(t) = Cx(t) + Du(t)5状态空间表达式的系统结构图状态和输出方程可以用结构图表示，形象地表明系统中信号传递关线性时变系统结构图6根据物理机理建立状态空间表达式对不同控制系统，根据其机理，即相应的物理或化学定律，可建立系统的状态空间表达式，步骤如下：1)确定系统输入、输出和状态变量；2)列出方程；3)消去中间变量；4)整理成标准的状态和输出方程。

7化输入-输出描述为状态空间描述设单输入—单数出线性定常连续系统的微分方程有下列一般形式X iX 2i 0丨0 i 00 ,Ac = a・.ai + I- ,bc = 90 i 0 0 (i)■1 —anL —an-2 一 ai _ ii 一yC)+a n 」yO+a n _2y d' + ai y+a o y= B n 」u O+B n/W)+…%u+B°u"S n」“s n」 ¥「0 N s s na n 』s n -1a n 2s n-2 a 〔s a 0= D s当选取不同的状态变量时，可以得到不同的状态空间形式1）能控规范性（P11）y = ：2人 r「X 2：°X i写成向量形式x = Ax Bu选状态变量 X i = z, X 2二z（1）,(n_2) (nJ),X nj = Z,X n = ZX i X 2X nd Xn=X n(n)二 z = —a n X i —anM-a i X n Uz (n)n』z ( nV)十•一 +a i ^«0^ U、、y = Pn/Z (n')十…+ 3忆 +-0 0Xn -AX n 0 i输出方程2)能观规范性 (P10)”xn = yx. = x i ^+a i y -^u i =1,…，n —1能控与能观两种规范型的系数矩阵存在下列关系A c = AObc = Ccc = b 0这种关系称为对偶原理。

3）对角型只系统含相异实极点时，可化为 A 是对角型的状态空间方程C i 二 lim(s- i)G(s), i =1,2, ,n S T A*定义X i 二 i X iu { ny ='5X iy =：%Xi「1X2 •…-■ n J x^ 1-0 - 1n _1C c X0 0 1 0代=0 1a *■ a 00 - a-j 0 - a ?aa1b °=七0 T0 c °= 0r一1G(s)二N(s) D(s)n=送i =14）约当型系统含重极点时c i lim (s - f ；i)G(s), i =k 1,r 2/ , n例：已知为传递函数C11. G2 . Q(s 1)2 s 1 s 2c 1^lim(s 1)2G(s) =5 C 12 “iqfts 1)2G(s)L-5 4d c^lim (s 2)G(s) -5A = 0 1_c j1c 2b =-c =和11S n _G(s)」(s)C12I T JC1kD(s) (s- if (s- 1)n亠i -k U 1S - ■■■■■ i‘1C 11C1kG(s)二5 (s 1)2(s 2)8从状态空间表达式求传递函数矩阵已知线性定常系统状态空间模型为x= Ax + Buy 二Cx DusX(s)- X(0) = AX(s) BU(s)Y(s) =CX(s) DU (s)令X(0)=0，则sX(s)二AX(s) BU(s)二X(s) = (si - A)・B U(S)二Y (s)二C(sl - A)—〔B D U (s)= G(s)U (s)G(s)二C(sl - A)，B D 系统的传递函数矩阵。

9线性系统的线性变换1）概念介绍状态变量的不同选取，其实是状态向量的一种线性变换，为坐标变或者称换。

设有一个n阶控制系统，两组不同状态变量分别是X1,X2, ,X ~1，~2， ,X n；则两组变量间存在非奇异线性变换关系:X 二Px = X 二P X,P 二IL. P n1 P nn 1于是，有如下线性方程：X i 二P ii X i 山2~2 P ln~n』X2 = P21~1 * P22~2 +…*P2n~nI -Xn 二P ni~i P n2~2 P nn~n即一组状态变量是另一组的线性组合，且这种组合具有唯一的对应关系，均能完全描述同一系统的行为。

状态向量的这种变换称为状态的线性变换或等价变换。

状态的线性变换或等价变换，实质是状态空间的基底变换，也即坐标变换。

状态变换后，状态空间表达式发生变化:原系统: 线性变换：X = P~,~ = P_1x~ = P‘AP~ + P，Bu:= A~ + Bu n」〜y = CP〜Du :二（〜〜Du 由此，有A 二P_1AP,B 二P_1B,（〜-CP,〜-D变换前后系统矩阵相似，故具有相同的基本特性，如行列式相同、秩相同、迹相同、特征多项式相同和特征值相同等。

对于线性定常系统x 二Ax Buy = Cx系统的特征多项式为：丸I _ A = detgl _ A)=丸门+ a附-1+ a?切-？+…+ a n丿+ a n系统的特征方程为：det( I - A) = 0特征方程的根，称为系统的特征值。

系统特征值的不变性：线性变换后det(sl - A) = det(sl - P’AP)二detP'(sl - A)P】二det(P‘)det(sl - A)det(P)二det( si - A)2)化为对角线标准型对线性定常系统，若系统的特征值两两互异，则必存在非奇异变换，将状态方程化为对角线标准型。

实际上P =匕P2P」R n n, AR 二i P•P P2…巳】.0 03）化为Jordan标准型如果系统矩阵A有重根，且A的线性独立的特征向量数等于系统的阶数n，则可将其化为对角线标准型。

当A有重根时，经线性变换一般可将A化为约当标准型J，矩阵J是主对角线上均为约当块的准对角型矩阵，即P’AP 二J 二diag J「J2, ,J M J R“…*M 7 r是-的代数重数J i1. I *J i 二约当块具有形式「人110组合系统的状态空间方程与传递函数矩阵设有两个系统：八 Ax ： + By . -i ： , I =1y =C |X |D |U |它们的传递函数矩阵为G i (s)=C i (sl-A)‘B i D I1并联其状态空间模型和传递函数为B !I uB 一y =C i X iD 1 u ' C 2 X 2 ' D 2U = C 1 C 2 (D i ■ D 2) u_i“ si - A i 0 B i IG(s)二C(sl - A) BC i Cj(D i D 2)]0 si — A2」B 」y 2y i并联系统\x j +A2 X2二 G(sl - AJ’Br D i C2(sl - A)'B2 D2 = G i(s) G2(s)2串联串联系统其状态空间模型为%Ax 「B 1uA 1x 1B 1u =I=X 2 A 2x 2 + B 2y 〔A 2x 2 +B 2C 1 x^ B 2D 1uy = C 2x 2 D 2u 2 二 C 2x 2 D 2(C 1x< D 1u) -D 2C 1 C 2 lx D 2D 2u传递函数矩阵丫 (s)f(s) = G 2 ( S )U 2(S )9(S )Y 1(S ) g(s)G i (s)U i (s) =G 2(s)G i (s)U (s) G(s)g (s) G i (s)3反馈连接假设D 仁D2=0u反馈连接0 &B iA2 .l x? .]B 2 D ix 1= A 1x^ B 1u 1=A“B 〔u - B 1C 2x 2x 2 二 A 2x 2B 2u 2 二 A 2x 2B 2C 1x 1y 二 C i X i写成向量形式IA)X i ■ B 1U -■ B 1C 2X 2I x = I-A 2x 2 + B 2C 1X 1一y = C 1 0】x传递函数矩阵Y(s)二 Y(s)二 G(s)U i (s)二 G(S )U(S )-Y 2(S )1二 G(s)U(s)-G (S )G 2(S )Y(S )二 I G i (s)G 2(s)Y(s)=G i (s)U(s)从而，有'I G 1(S )G 2(S )Y(S ^G 1(S )U(S ) =G(s)二〔I G(S )G 2(S )F G (S )G(s)9(s)〔l G 2(S )G 1(S )1-1本章小结现代控制理论的数学工具：状态空间描述。

线性系统的状态空间描述

合集下载