圆曲线加缓和曲线

（建筑工程管理）道路工程测量(圆曲线缓和曲线计算公式)道路工程测量(圆曲线缓和曲线计算公式)内容：理解线路勘测设计阶段的主要测量工作（初测控制测量、带状地形图测绘、中线测设和纵横断面测量）；掌握路线交点、转点、转角、里程桩的概念和测设方法；掌握圆曲线的要素计算和主点测设方法；掌握圆曲线的切线支距法和偏角法的计算公式和测设方法；了解虚交的概念和处理方法；掌握缓和曲线的要素计算和主点测设方法；理解缓和曲线的切线支距法和偏角法的计算公式和测设方法；掌握路线纵断面的基平、中平测量和横断面测量方；了解全站仪中线测设和断面测量方法。

重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。

§9.1交点转点转角及里程桩的测设道路工程测量概述分为：路线勘测设计测量(routereconnaissanceanddesignsurvey)和道路施工测量(roadconstructionsurvey)。

勘测设计测量(routereconnaissanceanddesignsurvey)分为：初测(preliminarysurvey)和定测(locationsurvey)初测内容：控制测量(controlsurvey)、测带状地形图(topographicalmapofazone)和纵断面图(profile)、收集沿线地质水文资料、作纸上定线或现场定线，编制比较方案，为初步设计提供依据。

2、定测内容：于选定设计方案的路线上进行路线中线测量(centerlinesurvey)、测纵断面图(profile)、横断面图(cross-sectionprofile)及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。

（二）道路施工测量(roadconstructionsurvey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。

道路曲线要素各字母含义
道路曲线要素包括圆曲线和缓和曲线，其中圆曲线要素包括：曲线半径 R、曲线转角θ、切线长 T、曲线长 L、外矢距 E；缓和曲线要素包括：缓和曲线长度 Ls、缓和曲线角β、圆曲线内移量 p、切线增值q。

各字母的含义如下：
- R：圆曲线半径，指的是弯道中心线的半径；
- θ：曲线转角，指的是路线转角处两条切线的交角；
- T：切线长，指的是圆曲线起点或终点到切点的长度；
- L：曲线长，指的是圆曲线的长度；
- E：外矢距，指的是曲线中点到交点的距离；
- Ls：缓和曲线长度，指的是缓和曲线的长度；
- β：缓和曲线角，指的是缓和曲线切线与主线切线的夹角；
- p：圆曲线内移量，指的是缓和曲线起点处，半径由 R 减小到 R+p 的距离；
- q：切线增值，指的是缓和曲线终点处，半径由 R+p 增大到 R 的距离。

这些要素在道路设计和施工中起着重要的作用，它们的大小和形状直接影响到道路的安全性、舒适性和经济性。

为了保障车辆行驶安全，在直线与圆曲线之间加入一段半径由∞逐渐变化到R的曲线，这种曲线称为缓和曲线。

目前常用的缓和曲线多为螺旋线，它有一个特性，曲率半径ρ与曲线长度l成反比。

数学表达为：ρ∝1/l 或ρ·l = k ( k为常数)若缓和曲线长度为l0，与它相连的圆曲线半径为R，则有：ρ·l = R·l0 = k目前我国公路采用k = （V为车速，单位为km/h），铁路采用k = ，则公路缓和曲线的长度为l0 = R ,铁路缓和曲线的长度为：l0 = R 。

11.2.2 带缓和曲线的圆曲线的主点及主元素的计算带缓和曲线的圆曲线的主点有直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH、缓直点HZ 。

带缓和曲线的圆曲线的主元素及计算公式：切线长 T h = q＋(R＋p)·tan(α/2)曲线长 L h = 2l0＋R·(α－2β0)·π/180°外矢距 E h = (R＋p)·sec(α/2)－R切线加长 q = l0/2－l03/(240R2)圆曲线相对切线内移量 p = l02/(24R)切曲差 D h = 2T h －L h式中：α 为线路转向角；β0为缓和曲线角；其中q、p、β0缓和曲线参数。

11.2.3 缓和曲线参数推导dβ = dl/ρ = l/k·dl两边分别积分，得：β= l2/(2k) = l/(2ρ)当ρ = R时，则β =β0β0 = l0/(2R)若选用点为ZH原点，切线方向为X轴，垂直切线的方向为Y轴，建立坐标系，则：dx = dl·cosβ = cos[l2/(2k)]·dldy = dl·sinβ = sin[l2/(2k)]·dl考虑β很小，sinβ和cosβ即sin(l2/(2k))和cos(l2/(2k))可以用级数展开，等式两边分别积分，并把k = R·l0代入，得以曲线长度l为参数的缓和曲线方程式：X = l－l5/(40R2l02)＋……Y = l3/(6Rl0)＋……通常应用上式时，只取前一、二项，即：X = l－l5/(40R2l02)Y = l3/(6Rl0)另外，由图可知，q = X HY－R·sinβ0p = Y HY－R(1－cosβ0)以β0= l0/(2R)代入，并对sin[l0/(2R)]、cos[l0/(2R)]进行级数展开，取前一、二项整理可得：q = l0/2－l03/(240R2)p = l02/(24R)若仍用上述坐标系，对于圆曲线上任意一点i，则i点的坐标X i、Y i可以表示为：Xi = R·sinψi＋qYi = R·(1－cosψi)＋p11.2.4 带缓和曲线的圆曲线的主点桩号计算及检核ZH桩号 = JD桩号－T hHY桩号 = ZH桩号＋l0QZ桩号 = HY桩号＋L/2YH桩号 = QZ桩号＋L/2 = HY桩号＋L = ZH桩号＋l0＋LHZ桩号 = YH桩号＋l0 = ZH桩号＋L hJD桩号 = ZY桩号－T h＋D h（检核）11.2.5 带缓和曲线的圆曲线的主点的测设过程：(1)在JD点安置经纬仪（对中、整平），用盘左瞄准直圆方向，将水平度盘的读数配到0°00′00″，在此方向量取T h，定出ZH点；(2)从JD沿切线方向量取T h－X HY，然后再从此点沿切线垂直方向量取Y HY , 定出HY点；(3)倒转望远镜，转动照准部到度盘读数为α，量取T h，定出HZ点；(4)从JD沿切线方向量取T h－X HY，然后再从此点沿切线垂直方向量取Y HY , 定出YH点；(5)继续转动照准部到度盘读数为（α＋180°）/2，量取E h，定出QZ点。

一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。

1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。

S=A2/ρ（A：与汽车有关的参数）ρ=C/sC=A2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。

3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。

令：ρ=R，l h=s 则 l h=A2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。

缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。

a1=0,a2=v2/ρ,a s=Δa/t≤0.62）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。

4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。

《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。

5．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。

βx=s2/2Rl h（2）缓和曲线的总切线角β=l h/2R.180/л2）缓和曲线直角坐标任意一点P处取一微分弧段ds，其所对应的中心角为dβx dx=dscosβxdy=dssinβx3）缓和曲线常数（1）主曲线的内移值p及切线增长值q内移值：p=Y h-R(1-cosβh)=l h2/24R切线增长值：q=X h-Rsinβh=l h/2-lh3/240R2（2）缓和曲线的总偏角及总弦长总偏角：βh=l h/2R总弦长：C h=l h-l h3/90R2O为圆曲线的圆心，圆曲线所对圆心角（等于公路偏角）。

圆曲线、缓和曲线、竖曲线、非完整缓和曲线计算培训1、圆曲线计算程序：“X0”?P 曲线起点X坐标“Y0”?Q 曲线起点Y坐标“X1”?X 曲线交点X坐标“Y1”?Y 曲线交点Y坐标“QDLC”?Z 曲线起点桩号“R”?R 曲线半径“L1R2”?O 曲线前进方向：左为1、右为2Lbl 0“1N-X,2X-N”?S 1为大转小、2为小转大Pol(P-X,Q-Y):ClsJ+180→K 曲线切线方位角计算If S=1：Then Goto 1：Else Goto 2：IfEndLbl 1“N”?U：“E”?V 测量的大坐标(U-P)cos(K)+(V-Q)sin(K)+Z→Z[1]：(V-Q)cos(K)-(U-P)sin(K)→Z[2] If O=1：Then -R→D：Else R→D：IfEndtan-1（（Z[1]-Z）/Abs（D-Z[2]））→Z[3]Abs(D)sin(Z[3])+Z →Z[4]：Abs(D)(1-cos(Z[3])) →Z[5]If O=1：Then –Z[5]→Z[5]：Else Z[5]→Z[5]：IfEndPol(Z[4]-Z,Z[5]-D):ClsJ+180 →Z[6]Z+Z[3](Abs(D)π)/180→Z[7](Z[1]-Z[4])cos(Z[6])+(Z[2]-Z[5])sin(Z[6]) →Z[8]If O=1：Then –Z[8]→Z[8]：Else Z[8]→Z[8]：IfEnd“X=”:Z[7]◢计算后的X小坐标“Y=”:Z[8]◢计算后的X小坐标Goto 0Lbl 2“X”?U：“Y”?V 测量的小坐标180(U-Z)/(Rπ)→Z[1]：Rsin(Z[1])+Z→Z[2]：R(1-cos(Z[1]))→Z[3]If O=1：Then –Z[3]→Z[3]:–V→C:–R→D：Else Z[3]→Z[3]:V→C:R→D：IfEnd Pol(Z[2]-Z,Z[3]-D)：ClsJ+180→Z[4]Z[2]+Ccos(Z[4])→Z[5]：Z[3]+Csin(Z[4])→Z[6]P+(Z[5]-Z)cos(K)-Z[6]sin(K)→Z[7]Q+(Z[5]-Z)sin(K)+Z[6]coc(K)→Z[8]“N=”:Z[7] ◢计算后的X大坐标“E=”:Z[8]◢计算后的Y大坐标Goto 02、缓和曲线计算程序：“X0”?P 曲线起点X坐标“Y0”?Q 曲线起点Y坐标“X1”?X 曲线交点X坐标“Y1”?Y 曲线交点Y坐标“ZHZH”?Z 曲线起点桩号“R”?R 圆曲线段半径“L”?L 缓和曲线单边曲线长度“L1R2”?O 曲线前进方向左为1右为2Lbl 0“LCZH”?F 测量里程Abs(F-Z)→BIf B<L:Then Goto 1:Else Goto 4:IfEnd 缓和段及圆曲线段计算转换Lbl 1180B2/(2RLπ)→A:RL/B→E:B-B5/(40R2L2)+B9/(3456R4L4)- B13/(599040R6L6)+ B17/(175472640R8L8)- B21/(7.80337152*1010R10L10)→C （红色的为计算小半径增加精度）B3/(6RL)-B7/(336R3L3)+B11/(42240R5L5)- B15/(9676800R7L7)+ B19/(3535596640R9L9)- B23/(1.8802409472*1012R11L11)→D:C-Esin(A) →G（红色的为计算小半径增加精度）If O=1:Then Goto 2:Else Goto3:IfEndLbl 2-D→D:D-Ecos(A) →HGoto 7D→D:D+Ecos(A) →HGoto 7Lbl 4180(B-L/2)/(Rπ)→A:L/2-L3/(240R2)→E:L2/(24R)-L4/(2688R3)→M E+Rsin(A) →C:C-Rsin(A) →GIf O=1:Then Goto 5:Else Goto 6:IfEndLbl 5-(M+R(1-cos(A)) →D:D-Rcos(A) →HGoto 7Lbl 6M+R(1-cos(A)) →D:D+Rcos(A) →HGoto 7Lbl 7Pol(P-X,Q-Y):ClsJ+180→KP+Ccos(K)-Dsin(K) →Z[2]:Q+Csin(K)+Dcos(K) →Z[3]P+Gcos(K)-Hsin(K) →Z[4]:Q+Gsin(K)+Hcos(K) →Z[5]Pol(Z[2]-Z[4],Z[3]-Z[5]):ClsJ+180→Z[1]“U”?U:“V”?V 测量所得大地坐标(U-Z[2])cos(Z[1])+(V-Z[3])sin(Z[1]) →Z[6](V-Z[3])cos(Z[1])-(U-Z[2])sin(Z[1]) →Z[7]If F>Z:Then Goto 9:Else Goto A:IfEndLbl 9If O=1:Then Z[7]→Z[7]:-Z[6]→Z[6]:Else –Z[7]→Z[7]:Z[6]→Z[6] IfEndGoto BLbl AIf O=1:Then –Z[7] →Z[7]:Z[6] →Z[6]:Else Z[7] →Z[7]:-Z[6] →Z[6] IfEndGoto BLbl B“X=”:Z[7] ◢计算后轴线X坐标“Y=”:Z[6] ◢计算后轴线X坐标“0→Goto 0,1→BZZB”?S 0为还回计算过程、1为进行轴线坐标计算大坐标If S=0:Then Goto 0Else Goto 8:IfEndLbl 8“X”?T:“Y”?WIf F>Z:Then Goto C:Else Goto D:IfEndLbl CIf O=1:Then T→Z[8]:-W→Z[11]:Else -T→Z[8]:W→Z[11]:IfEndGoto ELbl DIf O=1:Then -T→Z[8]:W→Z[11]:Else T→Z[8]:-W→Z[11]:IfEndGoto ELbl EZ[2]+Z[11]cos(Z[1])-Z[8]sin(Z[1]) →Z[9]Z[3]+Z[11]sin(Z[1])+Z[8]cos(Z[1]) →Z[10]“N=”:Z[9] ◢计算后X大坐标“E=”:Z[10] ◢计算后Y大坐标Goto 03、竖曲线计算程序：“ZH1”?A 交点1桩号“H1”?B 交点1高程“ZH2”?C 交点2桩号“H2”?D 交点2高程“ZH3”?E 交点3桩号“H3”?F 交点3高程“R”?R 曲线半径(D-B)/(C-A) →Z[1]:(F-D)/( E-C) →Z[2]:Z[2]-Z[1] →W:Abs(RW/2)→T Lbl 0“ZHC”?G:“HC”?H 测量桩号及高程If G≤(C-T):Then Goto 1:Else Goto 2:IfEndLbl 1H-(G-A) Z[1]-B →Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0Lbl 2If G≥(C+T):Then Goto 3:Else Goto 4:IfEnd Lbl 3H-(G-C) Z[2]-D→Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0Lbl 4(G-(C-T))2/(2R) →Z[4](G-A) Z[1]+B →Z[5]If W>0:Then Goto 5:Else Goto 6:IfEndLbl 5H-(Z[5]+Z[4]) →Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0Lbl 6H-(Z[5]-Z[4]) →Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0非完整缓和曲线计算起点和交点方向大坐标Lbl 0“X1”?A 非完整缓和曲线起点X坐标“Y1”?B 非完整缓和曲线起点Y坐标“X2”?C 非完整缓和曲线终点X坐标“Y2”?D 非完整缓和曲线终点Y坐标“A”?E 缓和曲线A值“R”?F 缓和曲线半径“L1”?G 图纸标注缓和曲线长度“L1R2”?R 方向左1右2E2÷F→H 缓和曲线完整计算长度H-G→K 缓和曲线打断长度K-K5÷(40×E4)+K9÷(3456×E8) -K13÷(599040×E12)+K17÷(175472640×E16)-K21÷(78033715200×E20) →LK3÷(6×E2)-K7÷(336×E6)+K11÷(42240×E10)-K15÷(9676800×E14)+K19÷(3530096640×E18)-K23÷(1880240947200×E22) →MH-H5÷(40×E4)+H9÷(3456×E8) -H13÷(599040×E12)+H17÷(175472640×E16)-H21÷(78033715200×E20) →NH3÷(6×E2)-H7÷(336×E6)+H11÷(42240×E10)-H15÷(9676800×E14)+H19÷(3530096640×E18)-H23÷(1880240947200×E22) →OTan-1（（O-M）÷(N-L)）→PPol(A-C,B-D)J+180→QIf R=1Then Q+P→SElse Q-P→SIfEndAbs(Lcos(S)-Msin(S)-A) →TAbs(Lsin(S)-Mcos(S)-B) →UT+100cos(S) →VU+100sin(S) →W“A0”:T◢完整缓和曲线原点X坐标计算值“B0”:U◢完整缓和曲线原点Y坐标计算值“A1”:V◢完整缓和曲线交点方向X坐标计算值“B1”:W◢完整缓和曲线交点方向Y坐标计算值Goto 0。

带有缓和曲线的圆曲线逐桩坐标计算
例题：某山岭区二级公路，已知交点的坐标分别为JD1（40961.914,91066.103 ）、JD2 （40433.528,91250.097 ）、JD3（40547.416,91810.392），JD2里程为
K2+200.000, R=150m缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩坐标。

（《工程测量》第202页36题）
解：（1）转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算
方法一：偏角法（坐标正算）
（2）第一缓和段坐标计算-0=7 3822 5 = 160 48 03
X Y
(4)第二缓和段坐标计算.0 = 7 38 22
方法二：切线支距法（坐标系转换）
（2）第一缓和段坐标计算
：-12 =160 48 03
X j =X Z H+ xcosot12+ y si n%2X=X ZH+ xs in a12 - yco^t12（本题为左转曲线）
(3) 圆曲线段坐标计算
0=73822 p = 0.444m q = 19.988m
12 =160 48 03 ZH( 40576.543 , 91200.296)
X i = X ZH xcos：12 ysin：12 Y =Y ZH xsin：12一ycos：12
:12=78 30 37
X i =X HZ—xcosc(23 +ysin o(23 Y =Y HZ— xsin53 _yco^t23 (本题为左转曲线)。

公路缓和曲线段原理及缓和曲线计算公式一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。

1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。

S=A2/ρ（A：与汽车有关的参数）ρ=C/sC=A2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。

3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。

令：ρ=R，l h=s 则 l h=A2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。

缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。

a1=0,a2=v2/ρ,a s=Δa/t≤0.62）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。

4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。

《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。

5．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。

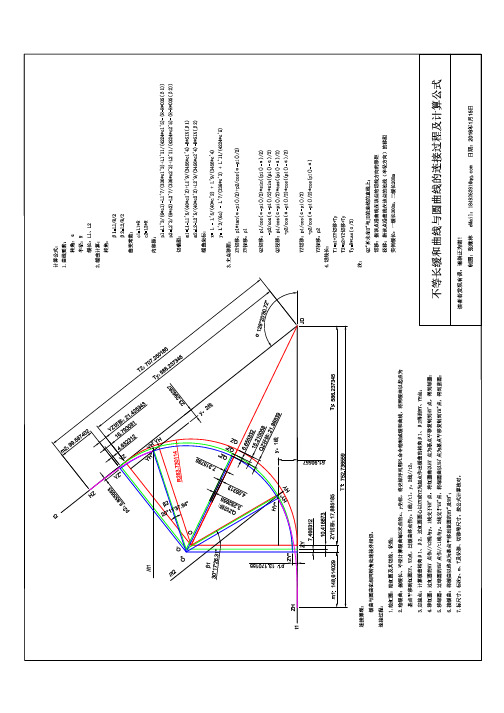
缓和曲线、圆曲线测设计算例题已知曲线半径R=6000，缓和曲线长度l0=280，交点JD27坐标及相邻方位角已在图中给出，ZH点里程为DK2+100。

请计算：1、曲线要素中的切线长T、曲线长L、外矢距E；2、HY、QZ、YH、HZ的里程；3、ZH点坐标及其左边桩3米的坐标；4、DK2+180的坐标及右边桩2米的坐标；5、DK2+660的坐标及右边桩35米的坐标。

永州(DK2+100)HYHZYHQZ08-715-.0α=232-附公式：m为缓和曲线切垂距，m= l0/2- l03/（240R2）p为缓和曲线内移距，P= l02/（24R）- l04/（2688R3）缓和曲线方程式：X=h - h5/（40R2l2）+ h9/（3456 R4l4）Y=h3/（6Rl）- h7/（336 R3l3）+ h11/（__ R5l5）解：1、转向角α=α2-α1=7°18′05.9″切线长T=（R+P）tg（α/2）+m = 522.863曲线长L=（Rαπ）/180+l0= 1044.626外矢距E=（R+P）sec（α/2）-R=12.746式中m为缓和曲线切垂距，m= l0/2- l03/（240R2）=139.9974p为缓和曲线内移距，P= l02/（24R）- l04/（2688R3）=0.54442、HY点里程为DK2+100+280=DK2+380；QZ点里程为DK2+100+1044.626/2=DK2+622.313；HZ点里程为DK2+100+1044.626=DK3+144.626；YH点里程为DK3+144.626-280=DK2+864.6263、JD27到ZH点的方位角αJD27到ZH点的坐标增量为：△x=T×cosα△y =T×sinα于是ZH点坐标为yZH= YJD27+△y =1415.299m Z35-1.922=αJD27(1000.000,1000.000)JD27-ZH=232°35′13.9″-180=52°35′13.9″ JD27-ZH=317.667m JD27-ZH=-415.299m XZH= xJD27+ △x =1317.667mZH点到左边桩3米的方位角α左边桩3米的坐标为：ZH-左边桩= 232°35′13.9″-90=142°35′13.9″X左= xZH+ 3×cosαY左= yZH +3×sinαZH-左边桩= 1315.284m ZH-左边桩=1417.122m4、DK2+180的坐标及右边桩2米的坐标:DK2+180在缓和曲线上，计算过程为：ZH点到JD27的方位角αZH-JD1= =232°35′13.9″DK2+180到ZH点的缓和曲线长度h为180-100=80根据缓和曲线方程式：X=h - h5/（40R2l2）+ h9/（3456 R4l4）=80.000Y=h3/（6Rl）- h7/（336 R3l3）+ h11/（__ R5l5）=0.0508由X和Y可以求出DK5+900与ZH的距离D和它的偏角δ：D=√（X2+ Y2）=80.000δ=arctg（Y/ X）=0°02′11.0″于是DK2+180的坐标（X1，Y1）为：X1= 1317.667+Dcos（232°35′13.9″-δ）=1269.022Y1 = 1415.299+Dsin（232°35′13.9″-δ）=1351.788DK2+300右边桩2米的坐标（X2，Y2）为：X2= 1269.022+2×cos（232°35′13.9″-3δ+90）=1270.608Y2= 1351.788+2×sin（232°35′13.9″-3δ+90）=1350.5705、圆曲线点DK2+660计算过程为：曲中点QZ的里程推算为DK2+622.313, DK2+660到QZ的圆曲线长度为660-622.313=37.687,所对应的圆心角为O′=（180*37.687）/（πR）=0°21′35.6″，JD27到圆心O的方位角αJD27-O=225°17′08.0″-（180-7°18′05.9″）/2=138°56′10.95″圆心O的坐标为：X3 =1000+（E+R）cos（138°56′10.95″）=-3533.494Y3= 1000+（E+R）sin（138°56′10.95″）=4949.753DK2+660的坐标（X4，Y4）为：X4= X3++ R cos（138°56′10.95″+180- O′）=965.544Y4 = Y3+Rsin（138°56′10.95″+180- O′）=980.035DK2+660右边桩35米的坐标（X5，Y5）为：X5= X3++ （R+35）× cos（138°56′10.95″+180- O′）=991.788 Y5= Y3+（R+35）×sin（138°56′10.95″+180- O′）=956.878。