4曲边梯形面积与定积分

4．5定积分与微积分基本定理[读教材·填要点]1．曲边梯形的面积(1)曲边梯形：位于曲线y ＝f (x )(a ≤x ≤b )和x 轴之间的图形，叫作函数y ＝f (x )在区间[a ，b ]上的“曲边梯形”．(2)曲边梯形面积的计算方法：化整为零、以直代曲，即把一个曲边梯形分成多个小曲边梯形，再用矩形代替小曲边梯形．2．计算变力所做的功的方法 化整为零，以直代曲． 3．定积分的概念设f (x )是在区间[a ，b ]上有定义的函数，在a ，b 之间取若干分点a ＝x 0＜x 1＜x 2＜…＜x n ＝b .记小区间[x k －1，x k ]为Δk ，其长度x k －x k －1记作Δx k ，Δx k 中最大的记作d ，再在每个小区间Δk z k ，作和式：∑k ＝1nf (z k )Δx k . ①如果(不论如何取分点x k 和代表点z k )当d 趋于0时和式①以S 为极限，就说函数f (x )在[a ，b ]上可积，并且说S 是f (x )在[a ，b ]上的定积分，记作S ＝⎠⎛a bf (x )d x .4．微积分基本定理如果f (x )是在[a ，b ]上有定义的连续函数，F (x )在[a ，b ]上可导并且F ′(x )＝f (x )， 则⎠⎛a bf (t )d t ＝F (b )－F (a )．[小问题·大思维]1．求曲边梯形面积时，对曲边梯形进行“以直代曲”，怎样才能尽量减小求得的曲边梯形面积的误差？提示：为了减小近似代替的误差，需要先分割再分别对每个小曲边梯形“以直代曲”，而且分割的曲边梯形数目越多，得到的面积的误差越小．2．求曲边梯形的面积与计算变速直线运动的路程有哪些相同点？提示：(1)求曲边梯形的面积与求变速直线运动的路程的共同本质是“以直代曲”“以不变代变”的思想方法．(2)求解的方法步骤相同．3．由定积分的定义可知，⎠⎛a b f (x )d x 是一个常数还是一个变量？⎠⎛a bf (x )d x 的值与哪些量有关？提示：由定义可得定积分⎠⎛a bf (x )d x 是一个常数，它的值仅取决于被积函数与积分上、下限，而与积分变量没有关系，即⎠⎛a bf (x )d x ＝⎠⎛a bf (t )d t ＝⎠⎛a bf (u )d u .4．如图所示，如何用阴影面积S 1，S 2，S 3表示定积分⎠⎛a bf (x )d x 的值？提示：⎠⎛a bf (x )d x ＝S 1－S 2＋S 3.计算下列定积分：(1) ⎠⎛－13(4x －x 2)d x; (2)⎠⎛12(x －1)5 d x ； (3)⎠⎛12(t ＋2)d x; (4)⎠⎛121x (x ＋1)d x . [自主解答] (1)取F (x )＝2x 2－x 33，因为F ′(x )＝4x －x 2，所以⎠⎛－13(4x －x 2)d x ＝F (3)－F (－1)＝⎝⎛⎭⎫2×32－333－⎣⎡⎦⎤2×(－1)2－(－1)33＝203. (2)因为⎣⎡⎦⎤16(x －1)6′＝(x －1)5， 所以⎠⎛12(x －1)5d x ＝F (2)－F (1)＝16×(2－1)6－16×(1－1)6＝16. (3)取F (x )＝(t ＋2)x ，因为F ′(x )＝t ＋2， 所以⎠⎛12(t ＋2)d x ＝F (2)－F (1) ＝2(t ＋2)－(t ＋2)＝t ＋2.(4)f (x )＝1x (x ＋1)＝1x －1x ＋1，取F (x )＝ln x －ln(x ＋1)＝ln x x ＋1， 则F ′(x )＝1x －1x ＋1.所以⎠⎛121x (x ＋1)d x ＝⎠⎛12⎝⎛⎭⎫1x －1x ＋1d x ＝F (2)－F (1)＝ln 43.运用微积分基本定理求定积分时的4个注意点(1)对被积函数要先化简，再求积分；(2)求被积函数为分段函数的定积分，依据定积分“对区间的可加性”，分段积分再求和；(3)对于含有绝对值符号的被积函数，要先去掉绝对值号再求积分； (4)注意用“F ′(x )＝f (x )”检验积分的对错．1．计算下列定积分：(1)⎠⎛－13(3x 2－2x ＋1)d x ； (2) ⎠⎛12⎝⎛⎭⎫x －1x d x ； (3) ⎠⎛0π (sin x －cos x )d x ； (4) ⎠⎛02|1－x |d x . 解：(1)取F (x )＝x 3－x 2＋x ， 则F ′(x )＝3x 2－2x ＋1.∴⎠⎛－13(3x 2－2x ＋1)d x ＝F (3)－F (－1)＝24.(2)取F (x )＝12x 2－ln x ，则F ′(x )＝x －1x .∴⎠⎛12⎝⎛⎭⎫x －1x d x ＝F (2)－F (1)＝32－ln 2. (3)取F (x )＝－cos x －sin x ， 则F ′(x )＝sin x －cos x .∴⎠⎛0π(sin x －cos x )d x ＝F (π)－F (0)＝2.(4)∵|1－x |＝⎩⎪⎨⎪⎧1－x ，0＜x ＜1，x －1，1＜x ＜2，∴取F 1(x )＝x －12x 2,0＜x ＜1，F 2(x )＝12x 2－x,1＜x ＜2，则F 1′(x )＝1－x ，F 2′(x )＝x －1.∴⎠⎛02|1－x |d x ＝F 1(1)－F 1(0)＋F 2(2)－F 2(1)＝1.已知函数f (x )＝ax 2＋c (a ≠0)，若⎠⎛01f (x )d x ＝f (x 0)，0≤x 0≤1，求x 0的值．[自主解答] 因为f (x )＝ax 2＋c (a ≠0)， 取F (x )＝a3x 3＋cx ，则F ′(x )＝ax 2＋c ，所以⎠⎛01f (x )d x ＝⎠⎛01(ax 2＋c )d x ＝F (1)－F (0)＝a 3＋c ＝ax 20＋c . 解得x 0＝33或x 0＝－33(舍去)． 即x 0＝33.利用定积分求参数时，注意方程思想的应用．一般地，首先要弄清楚积分变量和被积函数．当被积函数中含有参数时，必须分清常数和变量，再进行计算；其次要注意积分下限不大于积分上限．2．已知f (x )是一次函数，且⎠⎛01f (x )d x ＝5，⎠⎛01xf (x )d x ＝176，求f (x )的解析式． 解：设f (x )＝ax ＋b (a ≠0)， 取F 1(x )＝12ax 2＋bx ，∴F 1′(x )＝f (x )．则⎠⎛01(ax ＋b )d x ＝F 1(1)－F 1(0)＝12a ＋b ， ⎠⎛01x (ax ＋b )d x ＝⎠⎛01(ax 2＋bx )d x ， 取F 2(x )＝13ax 3＋12bx 2且F 2′(x )＝ax 2＋bx ，则⎠⎛01x (ax ＋b )d x ＝F 2(1)－F 2(0)＝13a ＋12b ，由⎩⎨⎧12a ＋b ＝5，13a ＋12b ＝176.解得a ＝4，b ＝3，故f (x )＝4x ＋3.求由抛物线y ＝x 2－4与直线y ＝－x ＋2所围成图形的面积．[自主解答] 由⎩⎪⎨⎪⎧y ＝x 2－4，y ＝－x ＋2，得⎩⎪⎨⎪⎧ x ＝－3，y ＝5或⎩⎪⎨⎪⎧x ＝2，y ＝0.所以直线y ＝－x ＋2与抛物线 y ＝x 2－4的交点为(－3,5)和(2,0)， 设所求图形面积为S ，根据图形可得S ＝⎠⎛－32[(－x ＋2)－(x 2－4)]d x ＝⎠⎛－32(6－x －x 2)d x ，取F (x )＝6x －12x 2－13x 3，则F ′(x )＝6－x －x 2， ∴S ＝F (2)－F (－3)＝1256.若将本例中“直线y ＝－x ＋2”换为“抛物线y ＝3－34x 2”，如何求解？解：如图所示，设所求图形面积为S ，S ＝⎠⎛－22⎣⎡⎦⎤⎝⎛⎭⎫3－34x 2－()x 2－4d x ＝⎠⎛－22⎝⎛⎭⎫7－74x 2d x ， 取F (x )＝7x －712x 3，则F ′(x )＝7－74x 2，∴S ＝F (2)－F (－2)＝563.利用定积分求由两条曲线围成的平面图形的面积的解题步骤 (1)画出图形．(2)确定图形范围，通过方程组求出交点的横坐标，确定积分上限和积分下限． (3)确定被积函数及积分变量，确定时可以综合考察下列因素：①被积函数的原函数易求；②较少的分割区域；③积分上限和积分下限比较简单． (4)写出平面图形的面积的定积分表达式．(5)运用微积分基本定理计算定积分，求出平面图形的面积．3．求曲线y ＝e x ，y ＝e－x及直线x ＝1所围成的图形的面积．解：由图可知，积分区间为[0,1]，面积S ＝⎠⎛10()e x －e －x d x ，取F (x )＝e x ＋e －x ， 则F ′(x )＝e x －e －x ， ∴S ＝F (1)－F (0)＝e ＋1e－2.变速直线运动的物体的速度为v (t )＝1－t 2，初始位置为x 0＝1，求它在前2秒内所走的路程及2秒末所在的位置．[自主解答] 当0≤t ≤1时，v (t )≥0， 当1≤t ≤2时，v (t )<0. 所以前2秒钟内所走的路程 S ＝⎠⎛01v (t )d t ＋⎠⎛12[－v (t )]d t＝⎠⎛01(1－t 2)d t ＋⎠⎛12(t 2－1)d t取F 1(t )＝t －13t 3，F 2(t )＝13t 3－t ，S ＝F 1(1)－F 1(0)＋F 2(2)－F 2(1)＝2.2秒末所在的位置：x 1＝x 0＋⎠⎛02v (t )d t ＝1＋⎠⎛02(1－t 2)d t ＝13. 即它在前2秒内所走的路程为2,2秒末所在位置为x 1＝13.1．有关路程、位移计算公式路程是位移的绝对值之和，从时刻t ＝a 到时刻t ＝b 所经过的路程s 和位移s 1分别为 (1)若v (t )≥0(a ≤t ≤b )，则s ＝⎠⎛a bv (t )d t ；s 1＝⎠⎛a bv (t )d t . (2)若v (t )≤0(a ≤t ≤b )， 则s ＝－⎠⎛a bv (t )d t ；s 1＝⎠⎛a bv (t )d t .(3)在区间[a ，c ]上，v (t )≥0，在区间[c ，b ]上，v (t )<0， 则s ＝⎠⎛a cv (t )d t －⎠⎛c bv (t )d t ；s 1＝⎠⎛a bv (t )d t . 2．求变力做功的方法步骤(1)要明确变力的函数式F (x )，确定物体在力的方向上的位移． (2)利用变力做功的公式W ＝⎠⎛ab F (x )d x 计算．[注意] 将力与位移的单位换算为牛顿(N)与米(m)，功的单位才为焦耳(J)．4．一物体在变力F (x )＝5－x 2(力单位：N ，位移单位：m)作用下，沿与F (x )成30°角的方向做直线运动，则由x ＝1运动到x ＝2时F (x )做的功为( )A. 3 JB.233 JC.433JD ．2 3 J解析：W ＝⎠⎛12F (x )cos 30°d x ＝⎠⎛1232(5－x 2)d x ＝32⎝⎛⎭⎫5x －13x 3⎪⎪⎪21＝433(J)． 答案：C求抛物线y 2＝2x 与直线y ＝4－x 围成的平面图形的面积．[解] 由方程组⎩⎪⎨⎪⎧y 2＝2x ，y ＝4－x ，解出抛物线和直线的交点为(2,2)及(8，－4)．法一：选x 作为积分变量，由图可看出S ＝A 1＋A 2.在A 1部分：由于抛物线的上半支方程为y ＝2x ，下半支方程为y ＝－2x ，所以S A 1＝⎠⎛02[2x －(－2x )]d x ＝22⎠⎛02x 12d x .取F 1(x )＝23x 32，∴S A 1＝22[F 1(2)－F 1(0)]＝163. S A 2＝⎠⎛28[4－x －(－2x )]d x ， 取F 2(x )＝4x －12x 2＋223x 32.∴S A 2＝F 2(8)－F 2(2)＝383. ∴S ＝163＋383＝18.法二：选y 作积分变量， 将曲线方程写为x ＝y 22及x ＝4－y .S ＝2-4⎰⎣⎡⎦⎤(4－y )－y 22d y . 取F (y )＝4y －y 22－y 36，∴S ＝F (2)－F (－4)＝30－12＝18.1．定积分⎠⎛01(2x ＋e x)d x 的值为( )A ．e ＋2B ．e ＋1C ．eD ．e －1解析：取F (x )＝x 2＋e x，则F ′(x )＝2x ＋e x，⎠⎛01(2x ＋e x )d x ＝F (1)－F (0)＝(1＋e)－(0＋e 0)＝e.答案：C2．从空中自由下落的一物体，在第一秒末恰经过电视塔顶，在第二秒末物体落地，已知自由落体的运动速度为v ＝gt (g 为常数)，则电视塔高为( )A.12g B ．g C.32g D ．2g解析：取F (x )＝12gt 2，则F ′(x )＝gt ，所以电视塔高为⎠⎛12gt d t ＝F (2)－F (1)＝2g －12g ＝32g . 答案：C3．s 1＝⎠⎛01x d x ，s 2＝⎠⎛01x 2d x 的大小关系是( )A ．s 1＝s 2B ．s 21＝s 2C ．s 1>s 2D ．s 1<s 2解析：⎠⎛01x d x 表示由直线x ＝0，x ＝1，y ＝x 及x 轴所围成的图形的面积，而⎠⎛01x 2d x 表示的是由曲线y ＝x 2与直线x ＝0，x ＝1及x 轴所围成的图形的面积，因为在x ∈[0,1]内直线y ＝x 在曲线y ＝x 2的上方，所以s 1>s 2.答案：C4.⎠⎛－12x 4d x ＝________.解析：∵⎝⎛⎭⎫15x 5′＝x 4，取F (x )＝15x 5， ∴⎠⎛－12x 4d x ＝F (2)－F (－1)＝15[25－(－1)5]＝335. 答案：3355．若⎠⎛01(2x ＋k )d x ＝2，则k ＝________. 解析：取F (x )＝x 2＋kx ，则F ′(x )＝2x ＋k ， ∴⎠⎛01(2x ＋k )d x ＝F (1)－F (0)＝1＋k ＝2，∴k ＝1. 答案：16．求由曲线xy ＝1及直线x ＝y ，y ＝3所围成平面图形的面积．解：作出曲线xy ＝1，直线x ＝y ，y ＝3的草图，所求面积为图中阴影部分的面积．求交点坐标：由⎩⎪⎨⎪⎧xy ＝1，y ＝3，得⎩⎪⎨⎪⎧x ＝13，y ＝3，故A ⎝⎛⎭⎫13，3；由⎩⎪⎨⎪⎧ xy ＝1，y ＝x ，得⎩⎪⎨⎪⎧ x ＝1，y ＝1或⎩⎪⎨⎪⎧x ＝－1，y ＝－1(舍去)， 故B (1,1)；由⎩⎪⎨⎪⎧ y ＝x ，y ＝3得⎩⎪⎨⎪⎧x ＝3，y ＝3，故C (3,3)，故所求面积S ＝S 1＋S 2＝⎠⎜⎛131⎝⎛⎭⎫3－1x d x ＋⎠⎛13(3－x )d x ＝4－ln 3.一、选择题1.⎠⎛241x d x 等于( ) A ．－2ln 2 B ．2ln 2 C ．－ln 2D ．ln 2解析：⎠⎛241x d x ＝ln 4－ln 2＝ln 2. 答案：D2．一物体沿直线运动，其速度v (t )＝t ，这个物体在t ＝0到t ＝1这段时间内所走的路程为( )A.13B.12C. 1D.32解析：曲线v (t )＝t 与直线t ＝0，t ＝1，横轴围成的三角形面积S ＝12即为这段时间内物体所走的路程．答案：B3.如图所示，阴影部分的面积是( ) A ．2 3 B ．2－ 3 C.323D.353解析：S ＝⎠⎛－31 (3－x 2－2x )d x ，即F (x )＝3x －13x 3－x 2， 则F (1)＝3－13－1＝53，F (－3)＝－9＋9－9＝－9. ∴S ＝F (1)－F (－3)＝53＋9＝323.答案：C4．定积分⎠⎛－22|x 2－2x |d x ＝( )A ．5B ．6C ．7D ．8解析：|x 2－2x |＝⎩⎪⎨⎪⎧x 2－2x ，－2≤x ＜0，－x 2＋2x ，0≤x ≤2， 取F 1(x )＝13x 3－x 2，F 2(x )＝－13x 3＋x 2， 则F 1′(x )＝x 2－2x ，F 2′(x )＝－x 2＋2x .∴⎠⎛－22|x 2－2x |d x ＝⎠⎛－20 (x 2－2x )d x ＋⎠⎛02(－x 2＋2x )d x ＝F 1(0)－F 1(－2)＋F 2(2)－F 2(0)＝8.答案：D二、填空题5．函数y ＝x －x 2的图象与x 轴所围成的封闭图形的面积等于________．解析：由x －x 2＝0，得x ＝0或x ＝1.因此所围成的封闭图形的面积为⎠⎛01(x －x 2)d x . 取F (x )＝12x 2－13x 3， 则F ′(x )＝x －x 2，∴面积S ＝F (1)－F (0)＝16. 答案：166．设函数f (x )＝(x －1)x (x ＋1)，则满足∫a 0f ′(x )d x ＝0的实数a ＝________.解析：⎠⎛0af ′(x )d x ＝f (a )＝0，得a ＝0或1或－1，又由积分性质知a >0，故a ＝1.答案：17．计算⎠⎛02(2x －e x )d x ＝________. 解析：取F (x )＝x 2－e x ，则F ′(x )＝2x －e x ，所以⎠⎛02(2x －e x )d x ＝F (2)－F (0)＝5－e 2. 答案：5－e 28．曲线y ＝1x ＋2x ＋2e 2x ，直线x ＝1，x ＝e 和x 轴所围成的区域的面积是________．解析：由题意得，所求面积为⎠⎛1e⎝⎛⎭⎫1x ＋2x ＋2e 2x d x . 取F (x )＝ln x ＋x 2＋e 2x ，则F ′(x )＝1x ＋2x ＋2e 2x ，所以⎠⎛1e⎝⎛⎭⎫1x ＋2x ＋2e 2x d x ＝F (e)－F (1)＝e 2e . 答案：e 2e三、解答题9．计算下列定积分．(1)⎠⎛14⎝⎛⎭⎫2x －1x d x ； (2)⎠⎛01x 1＋x 2d x .解：(1)取F (x )＝2xln 2－2x ， 则F ′(x )＝2x －1x . ∴原式＝F (4)－F (1)＝⎝⎛⎭⎫16ln 2－2ln 2－(24－2)＝14ln 2－2. (2)取F (x )＝12ln(1＋x 2)，则F ′(x )＝x 1＋x 2. ∴⎠⎛01x 1＋x 2d x ＝F (1)－F (0)＝12ln 2.10．已知函数f (x )＝x 3－x 2＋x ＋1，求其在点(1,2)处的切线与函数g (x )＝x 2围成的图形的面积．解：f ′(x )＝3x 2－2x ＋1，∵(1,2)为曲线f (x )＝x 3－x 2＋x ＋1上的点，设过点(1,2)处的切线的斜率为k ，则k ＝f ′(1)＝2，∴过点(1,2)处的切线方程为y －2＝2(x －1)，即y ＝2x .y ＝2x 与函数g (x )＝x 2围成的图形如图：由⎩⎪⎨⎪⎧y ＝x 2，y ＝2x 可得交点A (2,4)． ∴y ＝2x 与函数g (x )＝x 2围成的图形的面积S ＝⎠⎛02(2x －x 2)． 取F (x )＝x 2－13x 3，则F ′(x )＝2x －x 2， ∴S ＝F (2)－F (0)＝43.。

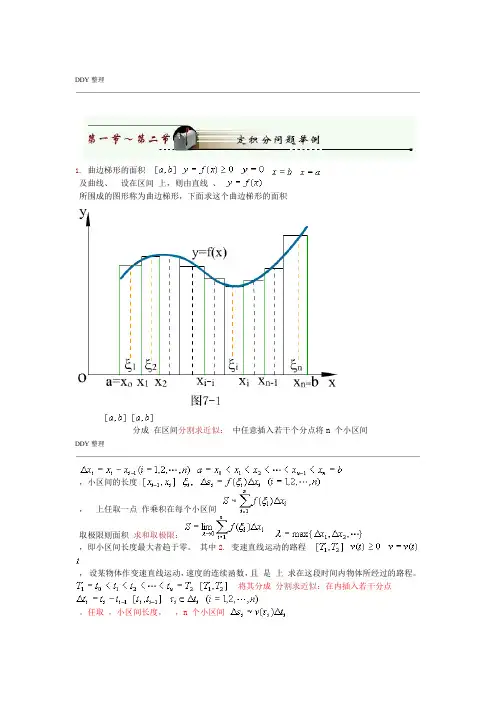
DDY整理1. 曲边梯形的面积及曲线、设在区间上，则由直线、所围成的图形称为曲边梯形，下面求这个曲边梯形的面积分成在区间分割求近似：中任意插入若干个分点将n 个小区间DDY整理，小区间的长度，上任取一点作乘积在每个小区间取极限则面积求和取极限：，即小区间长度最大者趋于零。

其中2.变速直线运动的路程，设某物体作变速直线运动，速度的连续函数，且是上求在这段时间内物体所经过的路程。

将其分成分割求近似：在内插入若干分点。

任取，小区间长度，，n 个小区间做取极限则路程求和取极限：DDY整理中任意插入若干个分点设函数在上有界，在定义，在每个小区间，其长度为n 个小区间将分成，作乘积，并求和，上任取一点上的，如果不论对怎样分法，也不论小区间记总趋于确定的极限，则称这个极限点时，和怎样取法，只要当为函数上的定积分，记作，即在区间，（*）叫积分变量，叫积分下限，叫被积函数，其中叫被积表达式，叫积分和式。

叫积分上限，叫积分区间。

说明：可积，下面两类函数在区间在区间）式右边极限存在，称1.如果（*上连续，则在区可积。

（2在区间（可积，1））在上可积。

在间上有界且只有有限个间断点，则2.由定义可知，定积分的值只与被积函数和积分区间有关，而与积分变量无关，所以DDY整理规定3. ,时两条直线、时 , 表示曲线在上、轴所围成的曲边梯形的面积；与、、两条直线在上时, 表示曲线轴的下方）曲边梯形在轴所围成的曲边梯形的面积（此时，；与DDY整理例1 利用定积分的几何意义写出下列积分值2））（1（半圆面积）（三角形面积）（DDY整理可积设 1性质2性质，有对任何三个不同的数性质3 （定积分对区间的可加性）性质4，则上，性质5 如果在区间推论上的最大在区间M 设及 m 分别是函数（定积分的估值）性质6值及最小值，则（定积分中值定理）性质7上至少有一点，上连续，则在在区间如果函数成立使DDY整理例2 比较下面两个积分的大小与，设解单调增 0，1）内，在（即有当，时，5由性质，的值3例估计积分设，只需求出在区间上的最大值、最小值即可。

《曲边梯形的面积》教学案例八中高中数学组兰北平“曲边梯形的面积”是定积分的内容，定积分在高中的教材里曾经几进几出，原因可能是这部分内容实在是太有用同时又存在不小的难度，就像是一种美味好吃却不易吃，会使人觉得弃之可惜。

新课程把其加进来，采用了不同于高等数学的处理方式，即不介绍不定积分，而直接通过一个几何问题和一个物理问题引入定积分的概念。

这充分体现新课程返璞归真，回归本质的理念。

不过这样无论对学生还是教师，都将是一个不小的挑战。

对于本节课的设计，笔者将重心放在如何使新课引入自然以及如何突破难点上。

一、对本节课的认识“曲边梯形的面积”是“定积分的概念”的第一课时。

定积分的思想方法是高等数学里的重要思想方法，是微积分的重要组成部分，在求解不规则图形的面积，变速运动的路程，变力做功等问题方面有着广泛的应用。

而求解曲边梯形面积的过程与思想恰恰是定积分概念的核心内容，所以本节课在定积分的学习中有着至关重要的地位和作用。

本节课内容较为单一，目标也比较明确，就是用“以直代曲，无限逼近”的思想求曲边梯形的面积。

然而，这种思想方法给学生带来的理解上的难度却不小，因为要真正理解这种方法必须对极限的思想要有比较清晰的认识。

不过，新课程似乎为了避免增加学生的负担，而不要求深入介绍极限的概念，其旨在用最易于让学生接受的手段，使学生获得最有价值的数学知识。

这节课亦是如此。

基于以上原因，备课时认为本节课有两大难点：一是如何使学生获得“无限分割，以直代曲”的思路；二是对“极限”“无限逼近”的理解，即理解为什么将近似值取极限正好是面积的精确值。

二、教学设计I、教学目标1.知识与技能：（1）了解定积分的实际背景；（2）会用分割-近似代替-求和-取极限的四步曲求曲边梯形的面积；2.过程与方法：（1）体会以直代曲的数学思想方法；（2）体会无限逼近的数学思想；3.情感、态度与价值观：通过以直代曲求曲边梯形面积的过程感受数学化归思想化难为易，化不可计算为可以计算的妙处；II、重点、难点1.重点：以直代曲的思想方法；求曲边梯形的四步曲；2.难点：以直代曲的思想方法；III、教学教法讲授与启发相结合，采用几何画板制作课件IV、教学过程（一）引入问题引入：这是浙江省地图，怎样求其面积？意图：用网格法求面积时边缘往往是不规则的图形，引出曲边梯形及求曲边梯形的面积问题. （二）新课问题1：我们会求正方形、三角形、平行四边形、梯形等“直边图形”的面积，现实生活中遇到的大量“曲边图形”，如何求“曲边图形”的面积？回答问题1：通过将曲边梯形分割成等宽的多个小曲边梯形，每个小曲边梯形的面积用高为左端点函数值矩形代替，求和，取极限得到面积.2、板书分割-近似代替-求和-取极限四步曲的详细步骤；3、用几何画板表格展示当n逐渐增大时，矩形面积和的值的变化趋势，验证计所得结果，并且发现面积和会从小于的方向逐渐接近1/3,思考为什么，引出下面探究问题. 探究：如果认为y=f(x)在每个小区间上的函数值近似地等于右端点的函数值，是否也能求出S=1/3?为什么？2、结合表格数据说明取区间右端点函数值得到的是过剩近似值，是从大于的方向趋近1/3；3、进一步说明取区间中的任何一点来近似也是可以的从而得到求面积的一般表达式01111lim ()lim ()3n n i i x n i i S f x f n ξξ∆→→∞===∆==∑∑为引出定积分的概念做铺垫. 练习：求直线x=0,x=2,y=0与曲线y=x(^2)所围成的曲边梯形的面积.38,21111382212→∞→⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⋅⎪⎭⎫ ⎝⎛=∑=n n i n S n n n n n i S意图：用一个与例题相仿，只是区间不同的例子进一步体验“分割—求和—近似—取极限”的方法.（三）小结：这节课我们学到了什么？1.求曲边梯形的面积的方法和步骤是：分割、近似代替、求和、取极限2.以直代曲，无限逼近的思想V 、布置作业作业本B 本P51，1、2、3、4、6、7、10三、教学片断实录及反思片断一：新课的引入师（提出问题）：这是浙江省地图，怎样求其面积？生：思考片刻，有的一脸茫然，有的在迟疑，个别窃窃私语：“用割补法”.师：“怎么割补？能否说得具体点？”生：不敢说或者不知道，不能给出答案.师：有一种近似求不规则图形面积的方法——“网格法”，接着介绍这种方法的具体做法。

定积分求特殊图形的面积几种常见的曲边梯形面积的计算方法： （1）x 型区域：①由一条曲线）其中0≥=)()((x f x f y 与直线)(,b a b x a x <==以及x 轴所围成的曲边梯形的面积：⎰badx x f S )(＝（如图（1））；②由一条曲线）其中0≤=)()((x f x f y 与直线)(,b a b x a x <==以及x 轴所围成的曲边梯形的面积：⎰⎰babadx x f dx x f S )()(＝－＝（如图（2））；③由两条曲线）其中，)()()(()(x g x f x g y x f y ≥==与直线)(,b a b x a x <==所围成的曲边梯形的面积：⎰badx x g x f S |)()(|－＝（如图（3））；（2）y 型区域：①由一条曲线）其中0≥=x x f y )((与直线)(,b a b y a y <==以及y 轴所围成的曲边梯形的面积,可由)(x f y =得)(y h x =，然后利用⎰bady y h S )(＝求出（如图（4））；②由一条曲线）其中0≤=x x f y )((与直线)(,b a b y a y <==以及y 轴所围成的曲边梯形的面积，可由)(x f y =先求出)(y h x =，然后利用⎰⎰babadyy h dy y h S )()(＝－＝求出（如图（5））；③由两条曲线)()(x g y x f y ==，与直线)(,b a b y a y <==所围成的曲边梯形的面积，可由)()(x g y x f y ==，先分别求出)(y h x 1=，)(y h x 2=，然后利用bdy y h y h S |)()(|－＝求出（如图（6））；图（4） 图（5） 图（6）例1．计算由两条抛物线2y x =和2y x =所围成的图形的面积.【分析】两条抛物线所围成的图形的面积，可以由以两条曲线所对应的曲边梯形的面积的差得到。

1.5.1曲边梯形的面积教学过程： 1．创设情景我们学过如何求正方形、长方形、三角形等的面积，这些图形都是由直线段围成的。

那么，如何求曲线围成的平面图形的面积呢？这就是定积分要解决的问题。

定积分在科学研究和实际生活中都有非常广泛的应用。

本节我们将学习定积分的基本概念以及定积分的简单应用，初步体会定积分的思想及其应用价值。

一个概念：如果函数()y f x =在某一区间I 上的图像是一条连续不断的曲线，那么就把函数()y f x =称为区间I 上的连续函数．（不加说明，下面研究的都是连续函数） 2．新课讲授问题：如图，阴影部分类似于一个梯形，但有一边是曲线()y f x =的一段，我们把由直线,(),0x a x b a b y ==≠=和曲线()y f x =所围成的图形称为曲边梯形．如何计算这个曲边梯形的面积？例1：求图中阴影部分是由抛物线2y x =，直线1=x 以及x 轴所围成的平面图形的面积S 。

分析：曲边梯形与“直边图形”的主要区别：曲边梯形有一边是曲线段，“直边图形”的所有边都是直线段．“以直代曲”的思想的应用．0.1把区间[]0,1分成许多个小区间，进而把区边梯形拆为一些小曲边梯形，对每个小曲边梯形“以直代取”，即用矩形的面积近似代替小曲边梯形的面积，得到每个小曲边梯形面积的近似值，对这些近似值求和，就得到曲边梯形面积的近似值．分割越细，面积的近似值就越精确。

当分割无限变细时，这个近似值就无限逼近所求曲边梯形的面积S ．也即：用划归为计算矩形面积和逼近的思想方法求出曲边梯形的面积． 解：（1）．分割 在区间[]0,1上等间隔地插入1n -个点，将区间[]0,1等分成n10,n ⎡⎤⎢⎥⎣⎦，12,n n ⎡⎤⎢⎥⎣⎦，…，1,1n n -⎡⎤⎢⎥⎣⎦记第i 个区间为1,(1,2,,)i i i n n n -⎡⎤=⎢⎥⎣⎦ ，其长度为11i i x n n n-∆=-=分别过上述1n -个分点作x 轴的垂线，从而得到n 个小曲边梯形，他们的面积分别记作：1S ∆，2S ∆，…，n S ∆显然，1nii S S ==∆∑（2）近似代替记()2f x x =，如图所示，当n 很大，即x ∆很小时，在区间1,i i n n -⎡⎤⎢⎥⎣⎦上，可以认为函数()2f x x =的值变化很小，近似的等于一个常数，不妨认为它近似的等于左端点1i n-处的函数值1i f n -⎛⎫⎪⎝⎭，从图形上看，就是用平行于x 轴的直线段近似的代替小曲边梯形的曲边（如图）．这样，在区间1,i i n n -⎡⎤⎢⎥⎣⎦上，用小矩形的面积i S '∆近似的代替i S ∆，即在局部范围内“以直代取”，则有211i i i i S S f x x n n --⎛⎫⎛⎫'∆≈∆=∆=∆ ⎪ ⎪⎝⎭⎝⎭ 211(1,2,,)i i n n n-⎛⎫== ⎪⎝⎭ ①（3）求和由①，上图中阴影部分的面积n S 为2111111nnnn i i i i i i S S f x n n n===--⎛⎫⎛⎫'∆=∆=∆= ⎪ ⎪⎝⎭⎝⎭∑∑∑=22111110n n n n n n -⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ =()22231121n n⎡⎤+++-⎣⎦ =()()312116n n n n --=1111132n n ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭从而得到S 的近似值 1111132n S S n n ⎛⎫⎛⎫≈=-- ⎪⎪⎝⎭⎝⎭4）取极限分别将区间[]0,1等分8，16，20，…等份（如图），可以看到，当n 趋向于无穷大时，即x ∆趋向于0时，1111132n S n n ⎛⎫⎛⎫=-- ⎪⎪⎝⎭⎝⎭趋向于S ，从而有 1111111lim lim lim 11323nn n n n i i S S f n n n n →∞→∞→∞=-⎛⎫⎛⎫⎛⎫===--= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ 从数值上的变化趋势：3．求曲边梯形面积的四个步骤:第一步：分割．在区间[],a b 中任意插入1n -各分点，将它们等分成n 个小区间[]1,i i x x -()1,2,,i n = ，区间[]1,i i x x -的长度1i i i x x x -∆=-，第二步：近似代替，“以直代取”。

(理)1.5定积分的概念1.5.1曲边梯形的面积1.5.2汽车行驶的路程【素养目标】1．理解连续函数的概念，了解定积分的实际背景及“以直代曲”“以不变代变”的思想方法，达成逻辑推理的核心素养。

2．会用分割、近似代替、求和、取极限的方法求曲边梯形的面积和汽车行驶的路程，培养学生的数学运算的核心素养。

【课前·预习案】[问题导学]知识点1.曲边梯形的面积观察图①和图②，其中阴影部分的面积可用梯形的面积公式来求，而图③中阴影部分有一边是曲线段．【思考1】如何求图③中阴影部分的面积呢？【提示】若把区间[a，b]分成许多小区间，进而把阴影部分拆分为一些小曲边梯形，近似地求出这些小曲边梯形的面积，分割的曲边梯形数目越多，所求得的面积越精确．〖梳理〗1、连续函数如果函数y＝f(x)在某个区间I上的图象是一条连续不断的曲线，那么就把它称为区间I上的连续函数．2、曲边梯形的面积1．曲边梯形：由直线x＝a，x＝b(a≠b)，y＝0和曲线y＝f(x)所围成的图形称为曲边梯形(如图①)．2．求曲边梯形面积的方法与步骤：(1)分割：把区间[a，b]分成许多小区间，进而把曲边梯形拆分为一些小曲边梯形 (如图②)；(2)近似代替：对每个小曲边梯形“以直代曲”，即用矩形的面积近似代替小曲边梯形的面积，得到每个小曲边梯形面积的近似值 (如图②)；(3)求和：把以近似代替得到的每个小曲边梯形面积的近似值求和；(4)取极限：当小曲边梯形的个数趋向无穷时，所有小曲边梯形的面积之和趋向一个定值，即为曲边梯形的面积．知识点2.求变速直线运动的路程如果物体做变速直线运动，速度函数为v＝v(t)，那么它在时间t所在的区间[a，b]内的路程(或位移)也可以运用(1)分割；(2)近似代替；(3)求和；(4)取极限的方法求得．[达标自评]1.判断下列说法是否正确，正确的在它后面的括号里打“√”，错误的打“×”：（1）在“近似代替”中，函数f(x)在区间[x i，x i ＋1]上的近似值只能是左端点的函数值f(x i)。