PIDA控制算法及仿真研究

实验三 数字式PID 调节器控制算法仿真一、实验目的1、了解并掌握基本的数字PID 控制算法和常用的PID 控制改进算法。

2、掌握用Matlab 进行仿真的方法。

3、了解PID 参数整定的方法及参数整定在整个系统中的重要性。

二、实验设备PC 机(Matlab 软件)三、实验原理1、基本的PID 控制算法：基本的数字P0控制有三种算法：位置式、增量式和速率式，其中应用最为广泛的是增量式，因为增量式算法只与最近几次采样值有关，不需要累加；计算机输出增量，误差动作时影响小。

因此这里采用增量式PID 算法：)]1()1(2)([)()]1()([)(-+--++--=∆k e k e k e k k e k k e k e k k u d i p其中设)]1()([)(--=k e k e k k u p p)()(k e k k u i i =)]2()1(2)([)(-+--=k e k e k e k k u d d则)()()()(k u k u k u k u d i p ++=∆2、数字PID 调节器参数的整定：为使系统性能满足一定的要求，必须确定算法中各参数的具体值，这就是参数整定。

参数整定是十分重要的，调节系统参数整定的好坏直接影响调节品质。

要想快速、灵活的将参数整定好，首先应透彻理解这些参数对系统性能的影响：增大比例系数，一般将加快系统的响应，这在有静差系统中有利于减小静差，但过大会使系统有较大超调，并产生振荡，使稳定性变坏。

增大积分时间(积分作用减弱)有利于减小超调，减小振荡，使系统更加稳定，但系统静差消除的过程将随之减慢。

增大微分时间(微分作用增强)有利于加快系统响应，使超调减小，稳定性增加，但系统对扰动有较敏感的响应。

四、实验要求1、在Matlab 环境中，按照给定对象，构建仿真PID 控制系统。

2、调整PID 参数，观察各参数对系统响应的影响。

3、采用增量式PID 算法进行控制系统仿真，对各参数进行整定，观察系统响应曲线，直到获得满意的响应曲线。

PID仿真实验报告PID控制是一种经典的控制方法，被广泛应用于工业自动化控制系统中。

本次实验主要针对PID控制器的参数调整方法进行仿真研究。

实验目的：1.研究PID控制器的工作原理；2.了解PID参数调整的方法；3.通过仿真实验比较不同PID参数对系统控制性能的影响。

实验原理：PID控制器由比例（P）、积分（I）、微分（D）三个控制部分组成。

比例控制：输出与误差成比例，用来修正系统集成误差；积分控制：输出与误差的积分关系成比例，用来修正系统持续存在的静态误差；微分控制：输出与误差变化率成比例，用来修正系统的瞬态过程。

PID参数调整方法有很多种，常见的有经验法、Ziegler-Nichols法和优化算法等。

实验中我们使用经验法进行调整，根据系统特性来进行手动参数调整。

实验装置与步骤：实验装置：MATLAB/Simulink软件、PID控制器模型、被控对象模型。

实验步骤：1. 在Simulink中建立PID控制器模型和被控对象模型；2.设定PID控制器的初始参数；3.运行仿真模型，并记录系统的响应曲线；4.根据系统响应曲线，手动调整PID参数；5.重复第3步和第4步，直到系统的响应满足要求。

实验结果与分析：从图中可以看出，系统的响应曲线中存在较大的超调量和震荡，说明初始的PID参数对系统控制性能影响较大。

从图中可以看出，系统的响应曲线较为平稳，没有出现明显的超调和震荡。

说明手动调整后的PID参数能够使系统达到较好的控制效果。

总结与结论：通过本次实验，我们对PID控制器的参数调整方法进行了研究。

通过手动调整PID参数，我们能够改善系统的控制性能，提高系统的响应速度和稳定性。

这为工业自动化控制系统的设计和优化提供了参考。

需要注意的是，PID参数的调整是一个复杂的工作，需要结合具体的控制对象和要求进行综合考虑。

而且，不同的参数调整方法可能适用于不同的控制对象和场景。

因此，在实际应用中，需要根据具体情况选择合适的参数调整方法，并进行实验验证。

17. 如何在仿真环境中测试PID控制？17、如何在仿真环境中测试 PID 控制？一、选择合适的仿真工具首先，需要选择一款适合的仿真工具。

常见的仿真软件包括MATLAB/Simulink、LabVIEW、AMESim 等。

这些工具都提供了强大的功能来构建系统模型和进行控制算法的仿真。

以 MATLAB/Simulink 为例，它具有丰富的模块库，方便用户快速搭建各种系统模型，并且提供了直观的图形界面，易于操作和调试。

二、确定被控制对象的模型在进行 PID 控制测试之前，必须明确被控制对象的数学模型。

被控制对象可以是机械系统、电气系统、热力系统等。

模型的准确性直接影响到测试结果的可靠性。

模型的建立可以基于物理定律和原理，通过推导得到数学表达式。

也可以通过实验数据进行系统辨识，得到近似的模型。

例如，对于一个简单的一阶惯性系统，其传递函数可以表示为：G(s) ＝ 1/（Ts ＋ 1)，其中 T 为时间常数。

三、设计 PID 控制器接下来就是设计 PID 控制器。

PID 控制器有三个参数：比例系数（Kp）、积分系数（Ki）和微分系数（Kd）。

比例系数主要影响系统的响应速度，系数越大，响应速度越快，但可能会导致超调量增大。

积分系数用于消除系统的稳态误差，但过大的积分系数可能会使系统不稳定。

微分系数可以改善系统的动态性能，抑制超调，但对噪声敏感。

通常可以采用经验法、试凑法或者基于一些优化算法来确定这三个参数的值。

四、搭建仿真模型在选定的仿真工具中，搭建被控制对象的模型和 PID 控制器，并将它们连接起来。

在 Simulink 中，可以从模块库中选择相应的模块，如传递函数模块、PID 控制器模块等，通过连线构建整个系统的仿真模型。

五、设置仿真参数设置仿真的时间范围、步长等参数。

时间范围应足够长，以充分观察系统的响应。

步长的选择要根据系统的特性和计算资源来权衡，过小的步长会增加计算时间，过大的步长可能会导致结果不准确。

智能PID整定方法的仿真与实验研究的开题报告一、研究背景与意义PID控制器被广泛应用于各种工业过程中，如化工、电力、机械等领域。

PID控制器具有简单易实现、易于调节等优点。

在实际应用中，PID控制器的控制效果和稳定性取决于PID参数的整定。

为了提高控制效果和稳定性，智能PID整定方法应运而生。

随着计算机技术和数学理论的发展，智能PID整定方法得到了广泛应用。

智能PID整定方法可以使控制系统更加稳定，提高控制精度，减少因温度等因素引起的控制器变化。

二、研究目的本研究旨在开发一种基于仿真和实验研究的智能PID整定方法。

通过模拟不同参数的控制回路并进行实验测试，得出最优的PID参数，以提高控制的效果和稳定性。

三、研究内容与方法1. 分析PID控制器的控制原理和算法。

2. 研究智能PID整定方法的理论和实现过程。

3. 利用MATLAB / Simulink建立PID控制回路的仿真模型，并进行结果分析和验证。

4. 在实验室中利用单片机等控制器搭建PID控制回路，对控制系统进行实验测试。

5. 结合仿真结果和实验结果，得出最优PID参数。

四、预期结果与结论本研究预期通过实验测试和仿真模型的结果分析，获得更优的PID参数，并将其应用到实际工业过程中，从而提高控制效果和稳定性，优化工业过程。

五、研究时间安排阶段|内容|时间节点--|--|--1|文献调研、PID控制原理学习|第1-2周2|智能PID整定方法研究、MATLAB / Simulink模型建立和仿真|第3-6周3|实验搭建、数据采集和分析|第7-10周4|数据分析和结论撰写|第11-12周5|论文写作和规范化|第13-14周六、预期的研究成果1. 提出一种基于仿真和实验的智能PID整定方法。

2. 构建PID控制回路的MATLAB / Simulink模型。

3. 利用单片机等控制器搭建PID控制回路进行实验，得出最优PID参数。

4. 发表学术论文1篇。

PID仿真实验报告PID控制算法是一种重要的控制算法，被广泛应用于工业控制系统中。

本文通过仿真实验的方式，对PID控制算法进行了验证和分析。

一、实验目的1.了解PID控制算法的基本原理和调节方法；2. 掌握MATLAB/Simulink软件的使用，进行PID控制实验仿真；3.验证PID控制算法的稳定性和性能。

二、实验内容本次实验选择一个常见的控制系统模型，以电感驱动的直流电机控制系统为例。

通过PID控制算法对该系统进行控制，观察系统的响应特性。

三、实验步骤1.搭建电感驱动的直流电机控制系统模型，包括电感、直流电机、PID控制器等组成部分；2.设置PID控制器的参数，包括比例增益Kp、积分时间Ti、微分时间Td等；3.进行仿真实验，输入适当的控制信号，观察系统的响应曲线；4.调节PID控制器的参数，尝试不同的调节方法，观察响应曲线的变化，寻找合适的参数。

四、实验结果与分析1.首先，设置PID控制器的参数为Kp=1，Ti=1，Td=0，进行仿真实验。

观察到系统的响应曲线，并记录与分析曲线的特点；2.其次，调整PID控制器的参数，如增大比例增益Kp，观察系统的响应曲线的变化；3.最后，调整积分时间Ti和微分时间Td，观察系统的响应曲线的变化。

通过实验结果与分析，可以得到以下结论：1.PID控制算法能够有效地控制系统，并实现稳定的控制；2.比例增益Kp对系统的超调量有较大的影响，增大Kp可以减小超调量，但也会增加系统的稳定时间；3.积分时间Ti对系统的稳态误差有较大的影响，增大Ti可以减小稳态误差，但也会增加系统的超调量；4.微分时间Td对系统的响应速度有较大的影响，增大Td可以增加系统的响应速度，但可能会引起系统的振荡。

五、实验总结通过本次实验，我深入理解了PID控制算法的原理和调节方法。

同时，通过对实验结果的分析，我也了解了PID控制算法的稳定性和性能。

在实际工程应用中，需要根据具体的控制对象，合理选择PID控制器的参数，并进行调节优化，以获得理想的控制效果。

摘要PID控制是最早发展起来的控制策略之一，由于其算法简单，鲁棒性好和可靠性高，被广泛应用于工业过程控制，尤其用于可简历精确数学模型的确定性控制系统。

而实际生产过程往往具有非线性、时变不确定性，难以建立精确的数学模型，应用常规PID控制器不能达到理想的控制效果。

为了达到使PID 控制能适应复杂的工况和高指标的控制要求，人们对PID控制进行了改进，出现了各种新型PID控制器，对于复杂对象，其控制效果远远超过常规PID控制。

本文主要选取两种先进PID控制算法：专家PID控制算法和模糊自整定PID控制算法，对典型纯迟延二阶系统对象进行控制仿真。

在化工、炼油、冶金、玻璃等一些复杂的工业工程当中，被控对象除了容积迟延外，往往不同程度的存在纯迟延，具有纯迟延的过程被公认为是较难控制的过程，因此，纯迟延系统一直受到人们的关注，成为重要的研究课题之一，对此类问题的研究具有重要的理论和实际意义。

我们选择以纯迟延系统为研究对象，并和常规PID控制进行对比，来得出先进PID控制算法更能适应非线性、时变不确定性的复杂系统的控制要求的结论。

关键词：智能控制；专家PID控制；模糊自整定PID控制；纯迟延二阶系统ABSTRACTThe PID control is a development to get up at the earliest stage of control one of the strategies.Because it's calculate way be simple.Drive extensive application at the industry process control.Particularly used for can mathematics model of the resume precision really settle sex control system.But the actual production line usually hasn't line,the hour change indetermination.Hard establishment the mathematics model of the precision.Application normal regulations PID the controller can't attain ideal of control effect.For attaining to make PID control ability orientation complications of work condition and Gao index sign of control request.People carried on an improvement to the PID control. Appeared various new PID controller.For complications object, it's control effect is far far above the normal regulations PID control.This text the main selection be two kinds of forerunner PID control calculate way:expert PID control calculate way and misty from whole settle PID control calculate way.Pure to typical model delay two rank system the object carry on control to imitate true.At chemical engineering, oil refining, metallurgy, glass...etc. some complications of industry engineering in the middle.Drive control object in addition to capacity delay,usually dissimilarity degree of existence pure delay.The process had pure delay drive generally accepted for is more difficult control of process.Therefore,The pure delay system has been be subjected to people of concern.The research become importance one of the topics,to this kind problem of research have importance of theories with actual meaning.We choice with pure delay system for research bine carry on contrast with normal regulations PID e forerunner PID control calculate way more ability orientation not line,hour become indetermination complications the control of the system request of conclusion.Keywords:Intelligence control; Expert PID control; Misty from whole settle PID control; Pure delay two rank system目录摘要 (I)ABSTRACT .......................................................... I I 第1章绪论 . (1)1.1课题背景与意义 (1)1.2PID概述 (2)1.2.1 PID控制原理 (2)1.2.2 单神经元PID控制器 (3)1.2.3 模糊自适应PID控制器 (4)1.2.4 专家PID控制器 (5)1.3.典型纯迟延二阶对象 (6)第2章专家式智能自整定PID控制 (8)2.1专家智能控制 (8)2.2专家式智能整定PID控制器的典型结构 (9)2.2.1 基于模式识别的专家式智能自整定PID控制器 (9)2.2.2 专家系统智能自整定PID控制器 (11)2.3专家PID控制原理 (13)第3章模糊PID控制 (16)3.1模糊控制 (16)3.1.1 模糊控制的基本原理 (16)3.1.2 模糊控制器 (17)3.1.3 模糊控制对非线性复杂函数的逼近 (20)3.1.4 模糊参数整定的基本思想 (20)3.1.5 模糊参数整定器的设计 (21)3.2模糊控制算法采样时间的选取 (25)第4章先进PID控制的MATLAB仿真及说明 (28)4.1MATLAB简介 (28)4.2仿真模型及条件 (29)4.2.1 应用对象及仿真条件选取 (29)4.2.2 仿真比较及分析 (29)结论 (32)参考文献 (33)附录 (35)致谢 .............................................. 错误!未定义书签。

PID控制算法的简单分析和仿真！PID算法简单剖析如下：1、⾸先我们来看⼀下PID系统的基本组成模块：如图所⽰，图中相关参数的表⽰如下：r(t)：系统实际上需要的输出值，这是⼀个标准值，在我们设定了之后让这个系统去逼近的⼀个值（随时间变化的原因是，我们对系统的需求不同才会改变！）y(t)：系统当前的输出值，这个值应该需要趋近于我们设定的值，当我们没有增加PID控制模块之前，它是由被控对象通过r(t)输⼊直接产⽣的。

e(t)：系统由于某些扰动，导致的系统产⽣的偏差，实际输出的值和想要设定的初始值r(t)的差值。

u(t)：系统通过PID控制器输出的新的输⼊值，实际上他是在r(t)的基础上，针对当前的实际情况做出的改变。

Kp⽐例模块：系统PID⽐例因⼦，Kp能够对于产⽣的偏差e(t)能够迅速的作出反应，减少偏差。

Ki积分模块：系统PID积分因⼦，Ki能够⽤于消除静差，由于前⾯的误差有正有负，所以当前偏差的加⼊能够抵消部分，保持系统的稳定性，让系统有记忆功能。

Kd微分模块：系统微分因⼦，Kd能够体现出当前误差的变化趋势，引⼊有效早期修正信号，从⽽加快系统的动作速度，减少调节时间。

图中所⽰的信号关系公式如下所⽰：信号误差公式：模拟信号的PID控制器公式：离散信号的PID控制器公式：被控对象的信号公式：（简单的线性系统，⽐如电机的PWM调速系统）上述公式参数描述：Kp控制器⽐例系数、Ti控制器积分时间(积分系数）、Td控制器微分时间(微分系数）k采样序列号，k=0,1,2,3...、Uk第k次采样时刻系统输出值、ek第k次采样时刻偏差值、ek-1第k-1次采样时刻偏差值、Ki=Kp*T/Ti、Kd=Kp*Td/T2、离散信号的PID控制器算法仿真：1、位置式PID算法：PID系统产⽣的值，完全作为系统的输⼊参数，即采⽤u(k)代替了r(k)，如果计算机出现故障时，位置式PID控制将导致Uk的剧烈变化，这会引起执⾏机构的⼤幅度变化，造成巨⼤损失。

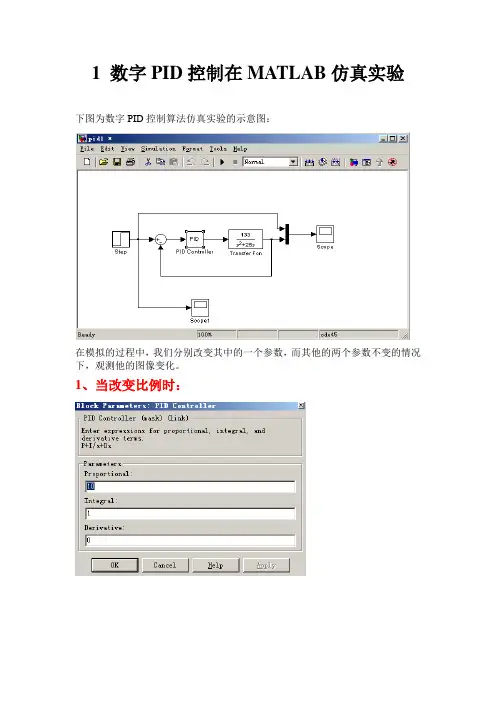
1 数字PID控制在MATLAB仿真实验下图为数字PID控制算法仿真实验的示意图：
在模拟的过程中，我们分别改变其中的一个参数，而其他的两个参数不变的情况下，观测他的图像变化。

1、当改变比例时：
分析结果：当只改变比例，积分和微分都不变的情况下，比例系数越大，调节作用越强，但是存在调节误差。

2、当只改变积分时
分析结果：当系统中只改变积分，而比例和微风都不变时，可以减少或消除误差，但响应慢。

3、当只改变微分时
分析结果：当系统中加入了微分环节时，改善了系统的稳定性能和动态性能，但是，它的响应比较慢。

PID控制系统的设计及仿真首先，我们需要理解PID控制器的工作原理。

PID控制器通过比较目标值与实际值之间的偏差，以及偏差的变化率和积分值来计算输出控制信号，从而实现目标值与实际值之间的闭环控制。

在设计PID控制系统时，我们需要确定三个参数：比例增益（KP）、积分时间常数（TI）和微分时间常数（TD）。

这些参数的选择将直接影响控制系统的稳定性和性能。

首先，我们可以使用频率响应曲线和Bode图等方法来选择合适的KP参数。

频率响应曲线可以帮助我们分析系统的稳定性和相位边界。

选择适当的KP值可以保证系统在稳定状态下能够尽快达到目标值。

接下来，我们可以通过试错法来确定TI和TD参数。

试错法可以根据系统的实际响应来调整这两个参数。

可以从初始调节试验开始，逐步调整参数，直到达到预期的系统性能。

在MATLAB中进行PID控制器的设计和仿真非常方便。

MATLAB提供了丰富的工具箱和函数，可以帮助我们进行系统建模、参数调节和仿真分析。

首先，我们需要使用MATLAB的控制系统工具箱来建立系统模型。

可以使用MATLAB提供的工具来建立连续或离散时间的传递函数模型。

接下来，我们可以使用PID函数来设计PID控制器并将其与系统模型进行连接。

PID函数可以使用我们之前确定的KP、TI和TD参数来创建一个PID对象。

然后，我们可以使用仿真命令来运行系统的仿真，并观察系统的响应。

可以使用step命令来观察系统的阶跃响应，使用impulse命令来观察系统的冲击响应，使用bode命令来观察系统的频率响应等等。

通过分析仿真结果，我们可以评估系统的稳定性、超调量、收敛时间等性能指标，并根据需要对PID参数进行进一步的调整。

总结起来，PID控制系统的设计及仿真可以通过MATLAB来完成。

我们可以使用MATLAB提供的工具箱和函数进行系统建模和参数调节，并通过仿真命令进行系统响应的观察和分析。

通过不断调整参数和分析仿真结果，我们可以设计出满足系统要求的PID控制系统。

PIDA控制及其整定与应用研究的开题报告一、选题背景和意义PIDA控制是指在传统的PID控制基础上增加一个先导项的控制模式。

在控制某些复杂的非线性系统时，传统的PID控制可能会存在一些问题，如超调、稳态误差等。

而PIDA控制则可以通过先导项的引入，有效地解决这些问题，提高控制系统的稳定性能和响应速度。

PIDA控制不仅在工业自动化控制、机械制造、航空航天等领域有广泛应用，还在环境保护、交通运输等领域也有着良好的应用前景。

因此，对于PIDA控制的研究与应用具有重要意义。

二、研究内容和方法本文将围绕PIDA控制的整定和应用展开研究。

具体的研究内容包括：1. PIDA控制器的数学描述和控制原理分析；2. PIDA控制器参数整定方法的研究，包括经验调整法、试探法、优化算法等；3. PIDA控制器在非线性系统控制中的应用研究；4. 采用MATLAB/Simulink进行PIDA控制器模型仿真分析。

研究方法包括文献调研、数学理论分析、仿真实验等。

三、研究进度计划1月份：文献调研，熟悉PIDA控制原理和应用领域。

2月份：对PIDA控制器的参数整定方法进行系统研究。

3月份：探究PIDA控制器在非线性系统控制中的应用。

4月份：进行PIDA控制器模型仿真分析，并对结果进行总结和分析。

5月份：撰写开题报告，并提交指导老师审核。

四、预期成果和创新点本文的预期成果为：1. 展示PIDA控制器的数学模型和控制原理。

2. 探究PIDA控制器的参数整定方法，给出实用性的整定方法。

3. 对PIDA控制器的应用进行研究，探寻其在非线性系统控制中的优势。

4. 通过MATLAB/Simulink仿真验证PIDA控制器的控制效果并进行总结和分析。

本文的创新点在于对PIDA控制器参数整定方法进行系统研究，并对其在非线性系统中的应用进行探究。

同时，本文将利用MATLAB/Simulink开展仿真实验，验证PIDA控制器在实际控制中的性能表现。

基于PID控制算法的温度控制系统的设计与仿真一、介绍温度控制是很多工业自动化系统中常见的任务之一、PID控制算法是目前最常用的控制算法之一，具有简单、稳定和高效的特点。

本文将以基于PID控制算法的温度控制系统为例，介绍其设计与仿真。

二、PID控制算法简介PID控制算法是一种经典的反馈控制算法，它根据当前系统的误差，计算出最佳的控制输出，以使系统的输出稳定在期望值附近。

PID控制算法由三个部分组成：比例（P）、积分（I）和微分（D）。

比例部分根据当前误差的大小调整输出控制量，积分部分通过累积误差来调整输出控制量，微分部分根据误差变化率调整输出控制量。

PID控制算法的输出控制量是由三个部分叠加而成。

1.系统模型的建立在设计温度控制系统之前，首先需要建立系统的数学模型。

以一个加热器控制系统为例，假设该系统的输入为加热功率，输出为温度。

2.控制器的设计根据系统模型，设计PID控制器。

首先调试比例参数P，使得系统的温度能够在误差范围内稳定下来；然后调试积分参数I，以减小系统的稳态误差；最后调试微分参数D，以提高系统的响应速度。

3.仿真实验在仿真软件中进行温度控制系统的仿真实验。

首先输入一个初始温度值，观察系统的响应；然后根据设定的期望温度，实时调整控制器的输出，观察系统的稳定状态。

4.结果分析根据仿真实验的结果，分析系统的稳态误差和响应速度。

根据实际需求和性能要求，调整控制器的参数，使得系统能够更好地满足要求。

四、结论本文以基于PID控制算法的温度控制系统为例，介绍了温度控制系统的设计与仿真过程。

通过调试PID控制器的参数，可以使系统的温度稳定在期望值附近，并且具有较好的稳态误差和响应速度。

PID控制算法在温度控制系统中有广泛的应用前景，但是需要根据具体的系统要求和性能要求进行参数调整和优化。

未来可以进一步研究温度控制系统的自适应PID控制算法，以提高控制系统的性能和鲁棒性。

PID控制算法的MATLAB仿真研究
PID控制算法是一种在自动控制理论中广泛使用的控制算法，它能够控制输出跟设定
的系统参数的偏差极其有效的缩小。

该控制算法的特点是反馈特性强、反应动静平衡等。

因此，比较多的研究学者采用MATLAB这款数字信号处理与计算工具来进行PID控制算法
的仿真研究。

对于PID控制算法的仿真，首先可以测试系统的品性能参数，包括平稳性和抗干扰能
力等。

随后，可以针对系统的特点，分析系统常用的各种控制算法，再选择出最优控制律，确定系统可调量与未知量。

接下来，可以使用MATLAB仿真各种传感器，传变等系统参数
对PID控制算法的性能，以及系统动态过程、稳态状态等参数作出分析与赋值。

最后，使用PID控制算法仿真MATLAB所做出的改进，可以综合考虑系统的控制要求，从理论与实践的角度，实现系统的动态响应特性、稳定性提高等，使系统更加稳定可靠。

通过PID控制算法仿真MATLAB，可以有效改善系统性能，提高系统调节效果、降低系统能耗、改善系统稳定性，提高系统控制精度等。

计算机控制课程设计--PID控制算法的MATLAB仿真研究《计算机控制技术》课程设计题目：PID控制算法的MATLAB仿真研究专业：自动化班级：三班学号：姓名：时间：2012年12月24日--2012年12月29日PID 控制算法的MATLAB 仿真研究一、课程设计目的和要求1.目的1)通过本课程设计进一步巩固PID 算法基本理论以及数字控制器实现的认识和掌握，归纳和总结PID 控制算法在实际运用中的一些特性； 2) 熟悉MATLAB 语言及其在控制系统设计中的应用，提高学生对控制系统程序设计的能力。

2.要求通过查阅资料，了解PID 算法研究现状和研究领域，充分理解设计内容，对PID 算法的基本原理与运用进行归纳和总结，并独立完成设计实验和总结报告。

二、课程设计的基本内容及步骤1. 任务的提出PID 控制算法是实际工业控制中应用最为广泛的控制算法，它具有控制器设计简单，控制效果好等优点。

PID 控制器参数的设置是否合适对其控制效果具有很大的影响，在本课设计中采用带纯滞后的一阶惯性环节作为系统的被控对象模型，传递函数为()1d sf Ke G s T sτ-=+，其中各参数分别为：30K =， 630fT=，60dτ=。

MATLAB 仿真框图如图1所示。

图12.对PID 控制算法的仿真研究从以下4个方面展开：（1）PID 控制器调节参数,,PI DKK K 的整定PID 参数的选定对控制系统能否得到好的控制效果是至关重要的，PID 参数的整定方法有很多种，可采用理论整定法（如ZN 法）或者实验确定法（比如扩充临界比例度法、试凑法等），也可采用如模糊自适应参数整定、遗传算法参数整定等新型的PID 参数整定方法。

在此处选用扩充临界比例度法对PID 进行整定，其过程如下：1Out1Zero-Order HoldTransport Delay30630s+1Transfer FcnStepScope1Kp1Kd1KI(z-1)zDiscrete Zero-Pole1z (z-1)Discrete Zero-PoleAdda) 选择一个足够短的采样周期Ts ，由于被控对象中含有纯滞后，且其滞后时间常数为τd =60，故可选择采样周期T s =1。