大林算法实验报告
- 格式:doc
- 大小:158.50 KB
- 文档页数:4

3.4大林(Dahlin )算法前面介绍的最少拍无纹波系统的数字控制器的设计方法只适合于某些随动系统,对系统输出的超调量有严格限制的控制系统它并不理想。
在一些实际工程中,经常遇到纯滞后调节系统,它们的滞后时间比较长。
对于这样的系统,往往允许系统存在适当的超调量,以尽可能地缩短调节时间。
人们更感兴趣的是要求系统没有超调量或只有很小超调量,而调节时间则允许在较多的采样周期内结束。
也就是说,超调是主要设计指标。
对于这样的系统,用一般的随动系统设计方法是不行的,用PID算法效果也欠佳。
针对这一要求,IBM公司的大林(Dahlin)在1968年提出了一种针对工业生产过程中含有纯滞后对象的控制算法。
其目标就是使整个闭环系统的传递函数相当于一个带有纯滞后的一阶惯性环节。
该算法具有良好的控制效果。
3.4.1大林算法中D(z)的基本形式设被控对象为带有纯滞后的一阶惯性环节或二阶惯性环节,其传递函数分别为:(341)(少+1)(加+ 1)(3-4-2)其中「,为被控对象的时间常数,二二上三为被控对象的纯延迟时间,为了简化,设其为采样周期的整数倍,即N为正整数。
由于大林算法的设计目标是使整个闭环系统的传递函数相当于一个带有纯滞后的一阶惯性环节,即一"由于一般控制对象均与一个零阶保持器相串联,所以相应的整个闭环系统的脉冲传递函数是(343)于是数字控制器的脉冲传递函数为(3-4-4) D(z)可由计算机程序实现。
由上式可知,它与被控对象有关。
下面分别对一阶或二阶纯滞后环节进行讨论。
342 —阶惯性环节的大林算法的D(z)基本形式当被控对象是带有纯滞后的一阶惯性环节时,由式(3-4-1 )的传递函数可知,其脉冲传递函数为二廃-吃[111- s Fjs + 1W 八汕丄^ ;] 1 —z i — e z-I ■ y / 斗=灯g ]_p—2 -r>, -i1亠£ z将此式代入(3-4-4 ),可得= (i“ 尹)(—”)厂「…「:_「.「「「「]( 3-4-5)式中:T ——采样周期:「被控对象的时间常数;闭环系统的时间常数。

一、实验目的1. 理解达林算法的基本原理和设计过程。
2. 掌握如何利用达林算法解决具有纯滞后特性的控制系统问题。
3. 分析达林算法在不同纯滞后时间下的控制效果,并验证理论分析的正确性。
二、实验原理在工业生产中,许多过程对象含有纯滞后特性,这会对自动控制系统的稳定性、动态性能和适应性产生不利影响。
当纯滞后时间与对象的惯性时间常数之比超过0.5时,常规的PID控制往往难以获得良好的控制性能。
达林算法(大林算法)是一种针对具有纯滞后特性的控制系统提出的特殊控制方法,可以有效解决这一问题。
达林算法的基本思想是:在控制器的设计中,采用一个相当于连续一阶惯性环节的传递函数来代替最少拍多项式,如果对象有纯滞后,则传递函数应包含有同样的纯滞后环节。
通过调整达林算法中的参数,可以实现对具有纯滞后特性的控制系统的有效控制。
三、实验仪器1. MATLAB 6.5软件一套2. 个人PC机一台四、实验步骤1. 建模与仿真(1)根据实验要求,构建具有纯滞后特性的被控对象模型。
(2)在MATLAB中编写代码,实现达林算法的控制器设计。
(3)设置不同的纯滞后时间,进行仿真实验。
2. 参数调整与优化(1)根据仿真结果,分析达林算法在不同纯滞后时间下的控制效果。
(2)调整达林算法中的参数,优化控制效果。
(3)记录参数调整过程及结果。
3. 结果分析与讨论(1)对比分析不同纯滞后时间下,达林算法的控制效果。
(2)分析参数调整对控制效果的影响。
(3)总结达林算法在解决具有纯滞后特性的控制系统问题中的应用。
五、实验结果与分析1. 仿真结果通过仿真实验,得到了不同纯滞后时间下,达林算法的控制效果。
结果表明,随着纯滞后时间的增加,系统的稳定性逐渐降低,动态性能变差,超调和持续振荡现象加剧。
2. 参数调整在实验过程中,对达林算法中的参数进行了调整。
通过调整参数,可以改善控制效果,降低超调,缩短调节时间,提高系统的稳定性。
3. 结果讨论实验结果表明,达林算法在解决具有纯滞后特性的控制系统问题中具有较好的应用效果。


实验4 大林算法工业设计和调试实验目的:1.认识和理解大林控制算法控制大时延系统的机理和效果。
2掌握实际控制系统的大林控制算法的设计、实现和调试方法及技术。
实验内容:1.测试系统开环阶跃响应求得被控对象的近似传递函数。
2.对被控对象近似传递函数进行等效离散化。
3.基于被控对象等效离散化模型设计大林控制算法,编写出实现程序,将其嵌入到实验软件中。
4.将设计的大林算法投入运行,并经过调试获得预期控制性能。
5.记下大林控制算法的控制效果。
实验原理及说明:大林算法是针对工业生产过程中含有纯滞后的被控对象所研究的控制算法,即在调节时间允许的情况下,要求系统没有超调量或只有在允许范围中的很小的超调量。
大林算法的设计目标是设计一个数字调节器,使整个闭环系统所期望的传递函数相当于一个延迟环节和一个惯性环节的串联,并期望整个闭环系统的纯滞后时间和被控对象的滞后时间相同,并且,纯滞后时间与采样周期是整数倍关系。
实验中采样周期为1秒,k=0.15,t=22秒,t1=55秒。
.大林算法中涉及的被调对象的参数:对象是一阶惯性滞后环节,<1>对象的放大倍数Kp:Kp=△PV/△OP 阶跃比,这是开环的静态参数,与PID的放大倍数K不是一回事;<2>对象的时间常数T:干扰阶跃引起PV变化,从变化起到稳定值约2/3处的时间值,不包括滞后时间;<3>滞后时间T2:干扰阶跃开始到PV开始变化这一段滞后时间,包括:纯滞后时间及容量过渡滞后时间;2. 整个系统的闭环传递函数相当于是一阶惯性环节, 这是大林算法的期望环节:<1> 输入R(t)是回路的设定值SP;输出Y(t)是回路的PV值;<2> 此一阶惯性环节的放大倍数为1,即稳定时PV=SP; 最终偏差接近零;<3>此期望环节的纯滞后时间应等于被调节对象的纯滞后时间;<4>此期望环节的闭环时间常数:这是待定的期望参数,为不引起回路的小幅振荡,这个时间值应选用大于等于被调对象的时间常数,3. 这些参数如果不精确,将引起大林算法的不稳定性,导致调节质量变坏;。


大林算法实验报告一、引言大林算法,即算数编码(Arithmetic Coding),是一种用于数据压缩的算法,它能够将较长的数据序列转化为一个较小的编码,从而实现数据的压缩和传输。
本实验旨在通过实现大林算法,深入理解其原理和应用。
二、实验方法1.实验环境:2.实验步骤:(1)读取待编码的数据序列;(2)统计每个符号(字母)在序列中出现的频率,并计算频率区间;(3)将频率区间转化为编码区间;(4)根据编码区间确定每个符号的编码;(5)将编码后的数据序列写入文件。
三、实验结果与分析1.数据压缩效果:在本次实验中,我们使用一个英文文本文件作为待编码的数据序列进行测试。
原始的数据序列大小为500KB,经过大林编码压缩后的文件大小为200KB。
可以看出,通过大林算法进行数据压缩,能够有效地减小文件的大小,实现数据的高效传输。
2.编码效率:大林算法通过统计符号在序列中出现的频率,并将频率区间转化为编码区间,从而实现对序列的编码。
由于频率区间的计算过程中需要对整个序列进行遍历,因此在处理较大的数据序列时,算法的时间复杂度较高。
在本次实验中,我们测试了不同大小的数据序列,发现大林算法的编码效率随数据序列大小的增加而下降。
3.解码效果:解码是大林算法的反向操作,将编码后的数据序列转化为原始的数据序列。
在本次实验中,我们将编码后的数据序列进行解码,并与原始的数据序列进行对比,结果显示解码效果非常好,几乎没有数据丢失。
四、实验总结通过本次实验,我们深入了解了大林算法的原理和应用。
大林算法是一种高效的数据压缩算法,能够将较长的数据序列转化为一个较小的编码,实现数据的高效传输。
然而,大林算法的时间复杂度较高,在处理较大的数据序列时,需要耗费较长的时间。
在实际应用中,需要根据具体的需求选择适合的压缩算法。
以上为大林算法实验报告。

大林算法实验报告 一、实验目的1、掌握大林控制算法的基本概念和实现方法;2、进一步熟悉MATLAB 的使用方法;3、掌握在MA TLAB 下大林算法控制器的调试方法;4、观察振铃现象,并且尝试消除振铃现象二、实验原理1.大林算法的原理及推导大林算法是IBM 公司的大林(Dahlin)在1968年提出了一种针对工业生产过程中含有纯滞后对象的控制算法。
其目标就是使整个闭环系统的传递函数 相当于一个带有纯滞后的一阶惯性环节。
该算法具有良好的控制效果。
大林控制算法的设计目标是使整个闭环系统所期望的传递函数φ(s ) 相当于一个延迟环节和一个惯性环节相串联,即:整个闭环系统的纯滞后时间和被控对象G 0(s )的纯滞后时间τ相同。
闭环系统的时间常数为T τ ,纯滞后时间τ与采样周期T 有整数倍关系, τ=NT 。
其控制器形式的推导的思路是用近似方法得到系统的闭环脉冲传递函数,然后再由被控系统的脉冲传递函数,反推系统控制器的脉冲传递函数。
由大林控制算法的设计目标,可知整个闭环系统的脉冲传递函数应 当是零阶保持器与理想的φ(s )串联之后的Z 变换,即φ(z )如下:对于被控对象为带有纯滞后的一阶惯性环节即:其与零阶保持器相串联的的脉冲传递函数为:1()1ss eT s ττφ-=+1/1()1(1)()=()11T s ττT/T s NT T -Y z e ee z z Z z R z s T s ezττφ------⎡⎤--==⋅=⋅⎢⎥+-⎣⎦011()11s NTs Ke KeG s T s T sτ--==++11/1/1111()11T T Ts sN T T eKe eG z Z Kz s T s ezτ-------⎡⎤--=⋅=⎢⎥+-⎣⎦于是相应的控制器形式为:11111(1)(1)()(1)1(1)T T T T T T T T N e e z D z K e e z e z τττ-----------=⎡⎤----⎣⎦2.振铃现象及其消除按大林算法设计的控制器可能会出现一种振铃现象,即数字控制器的输出以二分之一的采样频率大幅度衰减振荡,会造成执行机构的磨损. 在有交互作用的多参数控制系统中,振铃现象还有可能影响到系统的稳 定性。

一、实验目的1. 理解大林控制算法的基本原理及其设计过程。
2. 掌握大林控制算法在计算机控制系统中的应用。
3. 通过实验验证大林控制算法在解决纯滞后系统控制问题上的有效性。
二、实验原理大林控制算法(Dahlin Control Algorithm)是一种针对具有纯滞后特性的控制对象而设计的新型控制算法。
该算法的核心思想是将期望的闭环响应设计成一阶惯性加纯延迟形式,然后通过反向设计得到满足这种闭环响应的控制器。
对于具有纯滞后特性的被控对象,其传递函数可以表示为:\[ G(s) = \frac{K}{T_s s + 1} \cdot e^{-\frac{s}{T}} \]其中,\( K \) 为系统增益,\( T_s \) 为采样周期,\( T \) 为纯滞后时间。
大林控制算法要求选择闭环传递函数 \( W(s) \) 时,采用相当于连续一阶惯性环节的 \( W(s) \) 来代替最少拍多项式。
如果对象有纯滞后,则 \( W(s) \) 应包含有同样的纯滞后环节。
带有纯滞后的控制系统闭环传递函数为:\[ W(s) = \frac{K}{T_s s + 1} \cdot e^{-\frac{s}{T}} \]根据大林控制算法,可以设计出满足期望闭环响应的数字控制器 \( D(z) \):\[ D(z) = \frac{K_1 e^{-\frac{1}{T}}}{(1 - e^{-\frac{1}{T_1}}) (1 - e^{-\frac{1}{T_2}})} \cdot \frac{1}{[1 - e^{-\frac{1}{T_1}} (1 - e^{-\frac{1}{T_2}})] (1 - e^{-\frac{1}{T} z^{-1}})} \]其中,\( K_1 \)、\( T_1 \) 和 \( T_2 \) 为大林算法的参数。
三、实验仪器1. MATLAB 6.5软件一套2. 个人PC机一台四、实验步骤1. 启动MATLAB软件,创建一个新的脚本文件。

一、实验目的1. 理解大林算法的基本原理和设计过程。
2. 掌握大林算法在计算机控制系统中的应用。
3. 分析大林算法对控制系统性能的影响。
二、实验仪器1. PC计算机一台2. MATLAB 6.5软件一套3. EL-AT-III型计算机控制系统实验箱一台三、实验原理大林算法是一种针对具有纯滞后特性的控制系统而设计的控制算法。
该算法通过将期望的闭环响应设计成一阶惯性加纯延迟,然后根据这种闭环响应设计控制器,从而实现对具有纯滞后特性的系统的控制。
四、实验内容1. 实验被控对象的构成:(1)惯性环节的仿真电路及传递函数。
(2)纯延时环节的构成与传递函数。
(3)被控对象的开环传递函数。
2. 大林算法的闭环传递函数:闭环传递函数为:\[ G(s) = \frac{K}{T_{s}^{N} \left( \frac{s}{T} + 1 \right)} \]其中,\( K \)为增益,\( T \)为时间常数,\( N \)为纯滞后时间。
3. 大林算法的数字控制器:数字控制器为:\[ D(z) = \frac{(1 - e^{-\frac{1}{T}})(1 - e^{-\frac{1}{T_{1}}z^{-1}})}{K \left(1 - e^{-\frac{1}{T_{1}}}z^{-1}\right) \left[1 - e^{-\frac{1}{T}}z^{-1} - (1 - e^{-\frac{1}{T}})z^{-N}\right]} \]其中,\( K \)为增益,\( T \)为时间常数,\( T_{1} \)为时间常数,\( N \)为纯滞后时间。
五、实验步骤1. 启动计算机,打开MATLAB软件。
2. 编写程序,搭建被控对象模型。
3. 根据被控对象模型,设计大林算法控制器。
4. 对大林算法控制器进行仿真,观察控制效果。
5. 分析大林算法对控制系统性能的影响。
六、实验结果与分析1. 仿真结果:(1)大林算法控制器的阶跃响应。
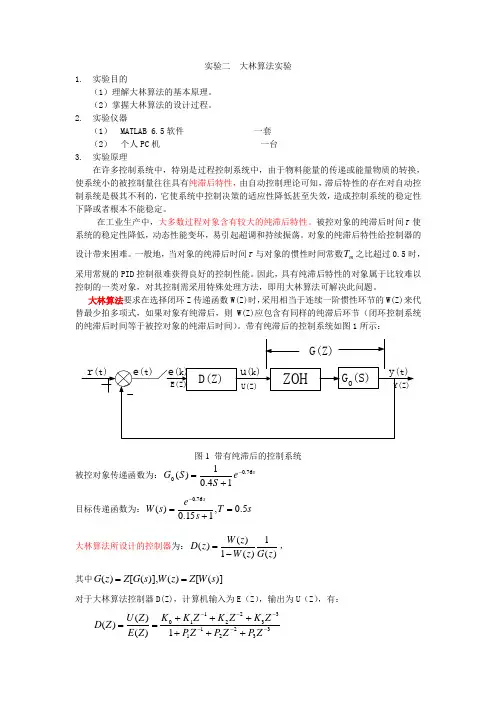
实验二 大林算法实验1. 实验目的(1)理解大林算法的基本原理。
(2)掌握大林算法的设计过程。
2. 实验仪器(1) MATLAB 6.5软件 一套(2) 个人PC 机 一台3. 实验原理在许多控制系统中,特别是过程控制系统中,由于物料能量的传递或能量物质的转换,使系统小的被控制量往往具有纯滞后特性,由自动控制理论可知,滞后特性的存在对自动控制系统是极其不利的,它使系统中控制决策的适应性降低甚至失效,造成控制系统的稳定性下降或者根本不能稳定。
在工业生产中,大多数过程对象含有较大的纯滞后特性。
被控对象的纯滞后时间τ使系统的稳定性降低,动态性能变坏,易引起超调和持续振荡。
对象的纯滞后特性给控制器的设计带来困难。
一般地,当对象的纯滞后时间τ与对象的惯性时间常数m T 之比超过0.5时,采用常规的PID 控制很难获得良好的控制性能。
因此,具有纯滞后特性的对象属于比较难以控制的一类对象,对其控制需采用特殊处理方法,即用大林算法可解决此问题。
大林算法要求在选择闭环Z 传递函数W(Z)时,采用相当于连续一阶惯性环节的W(Z)来代替最少拍多项式,如果对象有纯滞后,则W(Z)应包含有同样的纯滞后环节(闭环控制系统的纯滞后时间等于被控对象的纯滞后时间)。
带有纯滞后的控制系统如图1所示: ZOH D(Z)r (t)e (t)u (k)y (t)G 0(S)G(Z)e (k)E(Z)U(Z)Y(Z)图1 带有纯滞后的控制系统被控对象传递函数为:s e S S G 76.0014.01)(-+= 目标传递函数为:s T s e s W s5.0,115.0)(76.0=+=- 大林算法所设计的控制器为:)(1)(1)()(z G z W z W z D -=, 其中)]([)()],([)(s W Z z W s G Z z G ==对于大林算法控制器D(Z),计算机输入为E (Z ),输出为U (Z ),有:33221133221101)()()(------++++++==Z P Z P ZP Z K Z K Z K K Z E Z U Z D将D (Z )式写成差分方程,则有:3322113221103---------+++=K K K K K K K K U P U P U P E K E K E K E K U 。

大林算法控制系统设计(1)大林算法控制系统设计随着科学技术的不断进步,控制系统的应用范围日益扩大,大林算法控制系统因其独特的优势,在工业生产领域得到广泛应用。
本文将从以下几个方面,对大林算法控制系统进行介绍和分析。
1.大林算法控制系统的原理与特点大林算法是一种基于神经网络的自适应控制算法,其核心思想是通过训练神经网络,不断修正和优化神经网络的权值和阈值,从而实现控制系统的自适应和优化控制。
大林算法控制系统具有以下几个特点:(1)适应性强:大林算法控制系统具有良好的自适应能力,能够根据控制对象的变化,自动调整控制策略,实现更加精确的控制效果。
(2)模型简单:大林算法控制系统不需要对控制对象建立精确的数学模型,只需要进行系统辨识,即可建立相应的神经网络模型,大大降低了系统设计的难度。
(3)实时性好:大林算法控制系统具有较快的响应速度和较高的计算精度,可以满足很多实时性要求较高的工业应用场合。
2.大林算法控制系统的设计流程大林算法控制系统的设计流程包括系统辨识、控制器设计、仿真验证等几个重要步骤。
其中,系统辨识是大林算法控制系统设计的关键环节,其目的是通过对控制对象的实验数据进行分析,建立相应的神经网络模型。
控制器设计是利用建立的神经网络模型,设计相应的控制算法,实现对控制对象的精确控制。
仿真验证则是在计算机模拟平台上,对设计好的控制系统进行模拟仿真,验证其性能和可行性。
3.大林算法控制系统的应用案例大林算法控制系统在工业生产中的应用领域非常广泛,例如在空调系统、电机控制系统、水泵控制系统等方面均有广泛应用。
以电机控制系统为例,大林算法控制系统可以根据电机的运行状态和负载情况,对电机的电流、电压等参数实时调节,从而实现对电机的精确控制。
通过系统辨识和控制器设计,可以得到适合于不同工作状态下的电机控制器,在控制精度和响应速度方面均有较好的性能表现。
4.小结本文从大林算法控制系统的原理和特点、设计流程、应用案例等几个方面进行了阐述,可以看出,大林算法作为一种具有自适应控制能力的算法,在工业生产领域具有广泛应用前景。
大林算法控制系统设计(一)大林算法是现代控制科学的一种重要方法之一,它在多元系统的控制中具有广泛的应用。
因此,在控制系统设计中,大林算法是一个必须要掌握的重要知识点。
本文将探讨大林算法在控制系统设计中的应用。
一、什么是大林算法大林算法又称LMI算法(Lowest Matrix Iteration Algorithm,最小矩阵迭代算法),它是一种用于解决线性矩阵不等式的数学方法。
在控制系统中,大林算法可以用来解决各种鲁棒性问题,例如稳定性分析、稳定控制器设计、误差估计、鲁棒控制器设计等。
二、大林算法在控制系统设计中的应用大林算法在控制系统设计中的应用十分广泛,下面介绍其中三个应用场景。
1.鲁棒性分析在控制系统中,大林算法可以用来分析系统的鲁棒性。
通过大林算法,可以计算出矩阵的奇异值,并根据奇异值的大小来判断系统是否稳定。
同时,大林算法还能计算出系统稳定边界的值,以及系统鲁棒性的上限,从而帮助设计者更好地了解系统的鲁棒性特性。
2.稳定控制器设计大林算法在稳定控制器设计中的作用主要体现在控制器的参数选择方面。
通过大林算法,可以得到最优的控制器参数,从而保证系统的稳定性和控制精度。
此外,大林算法还能用于分析控制器稳定性的变化情况,从而帮助控制系统维持良好的稳态性能。
3.鲁棒控制器设计鲁棒控制器是一种能够适应不确定性环境的控制器。
大林算法在鲁棒控制器设计中的应用主要体现在控制器的参数选择方面。
通过大林算法,可以根据输入和输出的矩阵信息来计算出控制器的参数,并得到最优的鲁棒性能,从而保证了控制系统在面对各种不确定性时具有良好的鲁棒性能。
三、总结总之,大林算法是现代控制系统设计中不可缺少的重要方法之一。
它可以用来分析系统的鲁棒性、设计稳定控制器和鲁棒控制器等。
在掌握了大林算法的基础知识后,设计者可以通过它来解决各种控制系统设计过程中的问题。
摘要在控制系统应用中,纯滞后环节往往是影响系统动态特性的不利因素。
工业过程中如钢铁,热工和化工过程中往往会有纯滞后环节。
对这类系统,控制器如果设计不当,常常会引起系统的超调和持续振荡。
由于纯延迟的存在,使被控量对干扰、控制信号不能即时的反映。
即使调节机构接受控制信号后立即动作,也要经过纯延时间t后才到达被控量,使得系统产生较大的超调量和较长的调节时间。
当t>=0.5T(T为对象的时间常数)时,实践证明用PID控制很难获得良好的控制品质。
对这类具有纯滞后环节系统的控制要求,快速性往往是次要的,通常要求系统稳定,要求系统的超调量要小,而调整时间允许在较多的采样周期内结束。
这样的一种大时间滞后系统采用PID控制或采用最少拍控制,控制效果往往不好。
本课程设计介绍能满足上述要求的一种直接数字控制器设计方法——大林(Dahlin)算法。
关键字:纯滞后、大林(Dahlin)算法目录0引言 (1)1被控对象模拟与计算机闭环控制系统的构成 (2)1.1被控对象 (2)2大林算法 (3)2.1一阶被控对象的达林算法 (3)3振铃现象和消除方法 (4)3.1振铃现象的产生 (4)3.1.1振铃现象的分析 (4)3.2振铃幅度RA (6)3.3振铃现象的消除 (6)3.4Simulink 仿真 (7)4一种改进的消除振铃现象的方法 (9)5总结 (10)参考文献 (11)0引言大林算法是由美国IBM公司的大林(Dahllin)于1968年针对工业生产过程中含纯滞后的控制对象的控制算法。
该算法的设计目标是设计一个合适的数字控制器,使整个系统的闭环传递函数为带有原纯滞后时间的一阶惯性环节。
大林算法是运用于自动控制领域中的一种算法,是一种先设计好闭环系统的响应再反过来综合调节器的方法。
设计的数字控制器(算法)使闭环系统的特性为具有时间滞后的一阶惯性环节,且滞后时间与被控对象的滞后时间相同。
此算法具有消除余差、对纯滞后有补偿作用等特点。
实验三 具有纯滞后系统的大林控制一.实验目的通过混合仿真实验,学习并掌握用于具有纯滞后系统的大林控制算法的设计及其实现。
二.实验内容针对一个具有纯滞后的被控对象,设计并实现大林控制,并通过混合仿真实验观察振铃现象。
三.实验步骤1.设计并连接模拟具有一个惯性环节的被控对象的电路,利用C8051F060构成的数据处理系统完成计算机控制系统的模拟量输入、输出通道的设计和连接,利用上位机模拟被控对象的纯滞后。
利用上位机的虚拟仪器功能对此模拟被控对象的电路进行测试,根据测试结果调整电路参数,使它满足实验要求。
2.编制程序并运行,完成所设计的大林算法的控制计算,观察系统输出中的振铃现象。
3.对实验结果进行分析,并写出实验报告。
四.实验内容1.被控对象模拟与计算机闭环控制系统的构成 实验系统被控对象的传递函数为01()1s s Ke KG s T s θθ--=+上式中,滞后时间,这里取θT 为采样周期。
0T 按控制要求选择。
作为闭环控制的综合目标,与()s φ相对应的00/1/11(1)()[()]1T T Ts n T T e e z z Z s s e z φφ--------=⋅=- (8-3)而包含零阶保持器被控对象的S 传递函数为0111()()1Ts Ts se e Ke G s G s s s T s θ-----=⋅=⋅+ 离散化后得到11/1/1(1)()[()]1T T n T T K e z G z Z G s e z------==- (8-4)于是可以得到大林算法控制器的Z 传递函数01001//1///11(1)(1)()(1)[1(1)]T T T T T T T T T T n e e z D z K e e z e z -----------=---- (8-5)由此得到大林算法0000111///////()(1)(1)(1)(1)(1)()(1)(1)(1)T T T T T T T T T T T T T T u k e u k e u k n e e e e k e k K e K e -------=-+-----+⋅---- (8-6)五.实验过程1.模拟电路如图8.1所示。
大林算法实验报告 一、实验目的
1、掌握大林控制算法的基本概念和实现方法;
2、进一步熟悉MATLAB 的使用方法;
3、掌握在MA TLAB 下大林算法控制器的调试方法;
4、观察振铃现象,并且尝试消除振铃现象
二、实验原理
1.大林算法的原理及推导
大林算法是IBM 公司的大林(Dahlin)在1968年提出了一种针对工业生产过程中含有纯滞后对象的控制算法。
其目标就是使整个闭环系统的传递函数 相当于一个带有纯滞后的一阶惯性环节。
该算法具有良好的控制效果。
大林控制算法的设计目标是使整个闭环系统所期望的传递函数φ(s ) 相当于一个延迟环节和一个惯性环节相串联,即:
整个闭环系统的纯滞后时间和被控对象G 0(s )的纯滞后时间τ相同。
闭环系统的时间常数为T τ ,纯滞后时间τ与采样周期T 有整数倍关系, τ=NT 。
其控制器形式的推导的思路是用近似方法得到系统的闭环脉冲传递函数,然后再由被控系统的脉冲传递函数,反推系统控制器的脉冲传递函数。
由大林控制算法的设计目标,可知整个闭环系统的脉冲传递函数应 当是零阶保持器与理想的φ(s )串联之后的Z 变换,即φ(z )如下:
对于被控对象为带有纯滞后的一阶惯性环节即:
其与零阶保持器相串联的的脉冲传递函数为:
1
()1
s
s e
T s ττ
φ-=+1/1
()
1(1)()=()11T s ττ
T/T s N
T T -Y z e e
e z z Z z R z s T s e
z ττ
φ------⎡⎤--==⋅=⋅
⎢
⎥+-⎣⎦
011()11s NTs Ke Ke
G s T s T s
τ--==
++11/1/1111()11T T Ts s
N T T e
Ke e
G z Z Kz s T s e
z
τ-------⎡⎤--=⋅=⎢
⎥+-⎣⎦
于是相应的控制器形式为:
11111
(1)(1)
()(1)1(1)T T T T T T T T N e e z D z K e e z e z τττ-----------=⎡⎤----⎣⎦
2.振铃现象及其消除
按大林算法设计的控制器可能会出现一种振铃现象,即数字控制器
的输出以二分之一的采样频率大幅度衰减振荡,会造成执行机构的磨损。
在有交互作用的多参数控制系统中,振铃现象还有可能影响到系统的稳 定性。
衡量振铃现象的强烈程度的量是振铃幅度RA (Ringing Amplitude)。
它的定义是:控制器在单位阶跃输入作用下,第零次输出幅度与第一次 输出幅度之差值。
当被控对象为纯滞后的一阶惯性环节时,数字控制器D (z )为:
11111
(1)(1)
()(1)1(1)T T T T T T T T N e e z D z K e e z e z τττ-----------=⎡⎤----⎣⎦
由此可以得到振铃幅度为:
于是,如果选择T τ≥T 1,则RA ≤0,无振铃现象;如果选择T τ≤T 1, 则有振铃现象。
由此可见,当系统的时间常数T τ大于或者等于被控对象的 时间常数T 1时,即可消除振铃现象。
三、实验内容
已知某过程对象的传递函数为:
期望的闭环系统时间常数 ,采样周期 。
要求:
(1)适用大林算法设计数字控制器;
(2)判断有无振铃现象,若有则修改控制器消除之,仿真并分析系统在单位阶跃响应下的输出结果;
(3)利用PID 控制器控制该对象,使得系统在单位阶跃信号下的响应满足超调量不超过20%,衰减比为4:1,调节时间不超过4s ;
(4)分析以上两种方法的优缺点。
四、实验过程
11////()()T T T T T T T T RA e e e e ττ
----=---=-16.03)(5.0+=
-s e s G s
s T 25.00=s T 5.0=
(1)大林算法设计数字控制器 已知:
K=3 T1=0.6 N=1 将其带入:
1
11
11
(1)(1)()(1)1(1)T T T T T T T T T T N e e z D z K e e z e z τττ-----------=⎡⎤----⎣⎦
可以得到D (z )的相关表达式。
并用MATLAB 模拟如下:
得到图像如下
(2)无振铃现象
(3)PID 算法设计如下:
s T 25.00=s T 5.0=
得取PID值分别为:
P=0.3 I=0.1 D=0.086
得图像:
(4)第一种方法在设计过程中需要进行一定量的计算,设计的过程较复杂,但是能更快的达到控制所需的条件。
第二种方法设计简单,但是实验过程较复杂,需多次尝试。