简称为线性定常系统
- 格式:ppt
- 大小:562.00 KB
- 文档页数:10



1、反馈:输出信号被测量环节引回到输入端参与控制的作用。
2、开环控制系统与闭环控制系统的根本区别:有无反馈。
3、线性及非线性系统的定义及根本区别:当系统的数学模型能用线性微分方程描述时,该系统的称为线性系统。
非线性系统:一个系统,如果其输出不与其输入成正比,则它是非线性的。
根本区别:线性系统遵从叠加原理,而非线性系统不然。
4、传递函数的定义及特点:零初始条件下,系统输出量的拉斯变换与输入量的拉斯变换的比值。
用G〔s〕表示。
特点:1〕、传递函数是否有量纲取决于输入与输出的性质,同性质无量纲。
2〕、传递函数分母中S的阶数必n不小于分子中的S的阶数m,既n=>m ,因为系统具有惯性。
3〕、假设输入已给定,则系统的输出完全取决于其传递函数。
4〕、物理量性质不同的系统,环节和元件可以具有相同类型的传递函数。
5〕、传递函数的分母与分子分别反映系统本身与外界无关的固有特性和系统同外界的关系。
5、开环函数的定义:前向通道传递函数G〔s〕与反馈回路传递函数H(s)之积。
6、时间响应的定义和组成:系统在激励信号作用下,输出随时间的变化关系。
按振动来源分为:零状态响应和零输入响应。
按振动性质:自由响应和强迫响应。
7、瞬态性能指标以及反映系统什么特性:性能指标:上升时间tr、峰值时间tp、最大超调量Mp、调整时间ts、振荡次数N。
这些性能指标主要反映系统对输入的响应的快速性。
8、稳态误差的定义及计算公式:系统进入稳态后的误差。
稳态误差反映稳态响应偏离系统希望值的程度。
衡量控制精度的程度。
稳态误差不仅取决于系统自身结构参数,而且与输入信号有关。
系统误差:输入信号与反馈信号之差。
9、减少输入引起稳态误差的措施:增大干扰作用点之前的回路的放大倍数K1,以及增加这一段回路中积分环节的数目。
10、频率响应的概念:线性定常系统对谐波输入的稳态响应称为频率响应。
11、频率特性的组成:幅频特性和相频特性。
12、稳定性的概念:系统在扰动作用下,输出偏离原平衡状态,待扰动消除后,系统能回到原平衡状态〔无静差系统〕或到达新的平衡状态〔有静差系统〕。
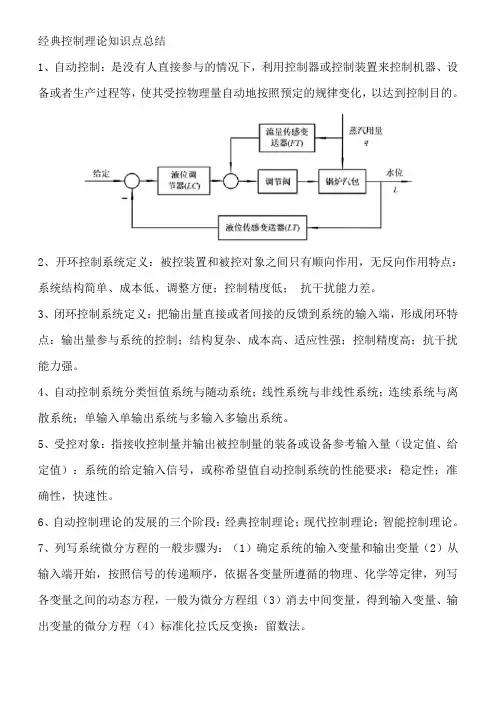
经典控制理论知识点总结1、自动控制:是没有人直接参与的情况下,利用控制器或控制装置来控制机器、设备或者生产过程等,使其受控物理量自动地按照预定的规律变化,以达到控制目的。
2、开环控制系统定义:被控装置和被控对象之间只有顺向作用,无反向作用特点:系统结构简单、成本低、调整方便;控制精度低;抗干扰能力差。
3、闭环控制系统定义:把输出量直接或者间接的反馈到系统的输入端,形成闭环特点:输出量参与系统的控制;结构复杂、成本高、适应性强;控制精度高;抗干扰能力强。
4、自动控制系统分类恒值系统与随动系统;线性系统与非线性系统;连续系统与离散系统;单输入单输出系统与多输入多输出系统。
5、受控对象:指接收控制量并输出被控制量的装备或设备参考输入量(设定值、给定值):系统的给定输入信号,或称希望值自动控制系统的性能要求:稳定性;准确性,快速性。
6、自动控制理论的发展的三个阶段:经典控制理论;现代控制理论;智能控制理论。
7、列写系统微分方程的一般步骤为:(1)确定系统的输入变量和输出变量(2)从输入端开始,按照信号的传递顺序,依据各变量所遵循的物理、化学等定律,列写各变量之间的动态方程,一般为微分方程组(3)消去中间变量,得到输入变量、输出变量的微分方程(4)标准化拉氏反变换:留数法。
8、传递函数的定义:在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比,称为线性定常系统的传递函数微分方程在时间域,传递函数在复数域传递函数的性质传递函数只适用于线性定常系统;传递函数是在零初始条件下定义的;传递函数可以有量纲;传递函数表示系统的端口关系;传递函数描述了系统的固有特性传递函数的表达式有理分式形式(特征多项式型)零、极点形式(首一型)时间常数形式(尾一型)。
9、动态性能的五个指标延迟时间(稳态值50%);上升时间(稳态值10%-90%,非一阶0-稳态值);峰值时间;调节时间;超调量(或最大超调量)。
10、一阶单位阶跃系统的动态性能指标:调节时间t=3T(5%误差带),t=4T(2%误差带)延迟时间t=0.69T上升时间t=2.20T峰值时间,超调量不存欠阻尼二阶系统的动态性能指标(P72)一对靠的很近或相等的零、极点,彼此将相互抵消,其结果使留数等于零,此类零、极点称为偶极子闭环主导极点,它应满足以下两个条件:(1)在s平面上,距离虚轴比较近,且附近没有其他的零点和极点(2)其实部的绝对值比其他极点实部的绝对值小5倍以上。




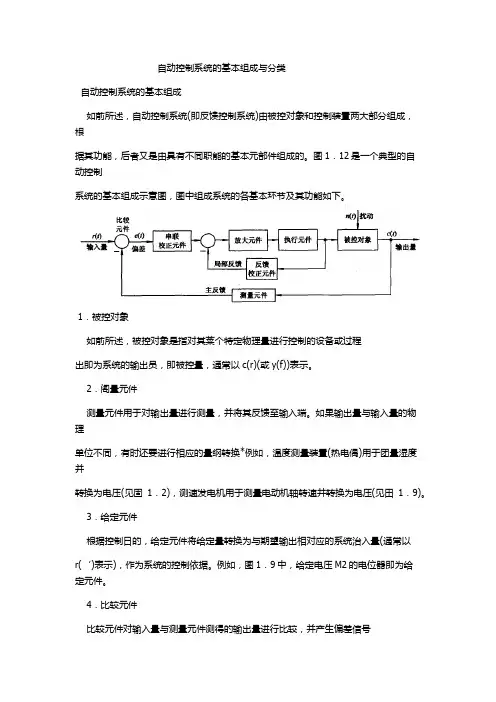
自动控制系统的基本组成与分类自动控制系统的基本组成如前所述,自动控制系统(即反馈控制系统)由被控对象和控制装置两大部分组成,根据其功能,后者又是由具有不同职能的基本元部件组成的。
图1.12是一个典型的自动控制系统的基本组成示意图,图中组成系统的各基本环节及其功能如下。
1.被控对象如前所述,被控对象是指对其莱个特定物理量进行控制的设备或过程出即为系统的输出员,即被控量,通常以c(r)(或y(f))表示。
2.阁量元件测量元件用于对输出量进行测量,并将其反馈至输入端。
如果输出量与输入量的物理单位不同,有时还要进行相应的量纲转换*例如,温度测量装置(热电偶)用于团量湿度并转换为电压(见固1.2),测速发电机用于测量电动机轴转速井转换为电压(见田1.9)。
3.给定元件根据控制日的,给定元件将给定量转换为与期望输出相对应的系统治入量(通常以r(‘)表示),作为系统的控制依据。
例如,图1.9中,给定电压M2的电位器即为给定元件。
4.比较元件比较元件对输入量与测量元件测得的输出量进行比较,并产生偏差信号中的电压比较电路。
通常,比较元件输出的偏差信号以‘(2)表示。
5.放大元件放大元件是特比较元件结出的(檄弱的)偏差信号进行放大(必要时还要进行物理量的转换)。
例如,图1.9中的ATMEL代理放大器和晶闸管整流装置等。
6.执行元件执行元件的功能是,根据放大元件放大后的偏差信号,推动执行元件去控制被控对象,使其被控量按照设定的要求变化。
通常,电动机、液压马达等都可作为执行元件。
7.校正元件校正元件又称补偿元件,用于改善系统的性能,通常以串联或反馈的方式连接在系统中。
在图1.12中,作用信号从输入端沿箭头方向到达输出端的传输通路称为前向通路;系统治出量经测旦元件反馈到输入端的传输通路称为主反馈通路;前向通路和主反馈通路构成的回路称为主反馈回路,简称主回路。
除此之外,还有局部反馈通路以及局部反馈回路等*将只包含一个主反馈通路的系统称为单回路系统,将包含两个或两个以上反馈通路的系统称为多回路系统。
简答线性定常系统的2个重要特性
线性定常系统是在系统响应测量时使用的重要类型,它含有两个重要特性,即线性特性和定常特性。
线性特性指的是,当外部激励增加时,系统的响应也增加,但增加量与激励的增加量可用恒定的微分方程来描述。
它意味着如果将激励量减少一半,系统的响应量将也减少一半。
它的功能可以通过椭圆形的将激励调制到椭圆形的响应曲线来表示。
另一个特性是定常性,即当外部环境噪声或其他激励源变化时,系统响应将保持不变。
这种特性是由系统内部结构和稳定度控制的。
它允许放大器系统根据信号输入的不断变化和信号输出的恒定比例响应。
因此,线性定常系统的特性综合了线性性能和定常性。
线性特性使系统对所有激励有线性响应,而定常特性则使系统可以将输入振幅调制到输出振幅,从而可以实现定常响应。
因此,线性定常系统广泛应用于测量技术中,可以获得较高精度的测量结果。