几何模型——半角模型

专题01 旋转中的三种全等模型（手拉手、半角、对角互补模型）本专题重点分析旋转中的三类全等模型（手拉手、半角、对角互补模型），结合各类模型展示旋转中的变与不变，并结合经典例题和专项训练深度分析基本图形和归纳主要步骤，同时规范了解题步骤，提高数学的综合解题能力。

模型1.手拉手模型【模型解读】将两个三角形（或多边形）绕着公共顶点旋转某一角度后能完全重合，则这两个三角形构成手拉手全等，也叫旋转型全等。

其中：公共顶点A记为“头”，每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”，第二个顶点记为“右手”。

手拉模型解题思路：SAS型全等（核心在于导角，即等角加（减）公共角）。

1）双等边三角形型条件：△ABC和△DCE均为等边三角形，C为公共点；连接BE，AD交于点F。

结论：①△ACD≌△BCE；②BE=AD；③∠AFM=∠BCM=60°；④CF平分∠BFD。

2）双等腰直角三角形型条件：△ABC和△DCE均为等腰直角三角形，C为公共点；连接BE，AD交于点N。

结论：①△ACD≌△BCE；②BE=AD；③∠ANM=∠BCM=90°；④CN平分∠BND。

3）双等腰三角形型条件：△ABC 和△DCE 均为等腰三角形，C 为公共点；连接BE ，AD 交于点F 。

结论：①△ACD ≌△BCE ；②BE =AD ；③∠ACM =∠BFM ；④CF 平分∠AFD 。

4）双正方形形型条件：△ABCFD 和△CEFG 都是正方形，C 为公共点；连接BG ，ED 交于点N 。

结论：①△△BCG ≌△DCE ；②BG =DE ；③∠BCM =∠DNM=90°；④CN 平分∠BNE 。

例1．（2022·黑龙江·中考真题）ABC V 和ADE V 都是等边三角形．(1)将ADE V 绕点A 旋转到图①的位置时，连接BD ，CE 并延长相交于点P （点P 与点A 重合），有PA PB PC +=（或PA PC PB +=）成立；请证明．(2)将ADE V 绕点A 旋转到图②的位置时，连接BD ，CE 相交于点P ，连接PA ，猜想线段PA 、PB 、PC 之间有怎样的数量关系？并加以证明；(3)将ADE V 绕点A 旋转到图③的位置时，连接BD ，CE 相交于点P ，连接PA ，猜想线段PA 、PB 、PC 之间有怎样的数量关系？直接写出结论，不需要证明．【答案】(1)证明见解析 (2)图②结论：PB PA PC =+，证明见解析 (3)图③结论：PA PB PC+=【分析】（1）由△ABC 是等边三角形，得AB =AC ，再因为点P 与点A 重合，所以PB =AB ，PC =AC ，PA =0，即可得出结论；（2）在BP 上截取BF CP =，连接AF ，证明BAD CAE V V ≌（SAS ），得ABD ACE Ð=Ð，再证明CAP BAF ≌△△（SAS ），得CAP BAF Ð=Ð，AF AP =，然后证明AFP V 是等边三角形，得PF AP =，即可得出结论；（3）在CP 上截取CF BP =，连接AF ，证明BAD CAE V V ≌（SAS ），得ABD ACE Ð=Ð，再证明BAP CAF ≌△△（SAS ），得出CAF BAP Ð=Ð，AP AF =，然后证明AFP V 是等边三角形，得PF AP =，即可得出结论：PA PB PF CF PC +=+=．(1)证明：∵△ABC 是等边三角形，∴AB =AC ，∵点P 与点A 重合，∴PB =AB ，PC =AC ，PA =0，∴PA PB PC +=或PA PC PB +=；(2)解：图②结论：PB PA PC=+证明：在BP 上截取BF CP =，连接AF ，∵ABC V 和ADE V 都是等边三角形，∴AB AC =，AD AE =，60BAC DAE Ð=Ð=°∴BAC CAD DAE CAD Ð+Ð=Ð+Ð，∴BAD CAE Ð=Ð，∴BAD CAE V V ≌（SAS ），∴ABD ACE Ð=Ð，∵AC =AB ，CP =BF ， ∴CAP BAF ≌△△（SAS ），∴CAP BAF Ð=Ð，AF AP =，∴CAP CAF BAF CAF Ð+Ð=Ð+Ð，∴60FAP BAC Ð=Ð=°，∴AFP V 是等边三角形，∴PF AP =，∴PA PC PF BF PB +=+=；(3)解：图③结论：PA PB PC +=，理由：在CP 上截取CF BP =，连接AF ，∵ABC V 和ADE V 都是等边三角形，∴AB AC =，AD AE =，60BAC DAE Ð=Ð=°∴BAC BAE DAE BAE Ð+Ð=Ð+Ð，∴BAD CAE Ð=Ð，∴BAD CAE V V ≌（SAS ），∴ABD ACE Ð=Ð，∵AB =AC ，BP =CF ，∴BAP CAF ≌△△（SAS ），∴CAF BAP Ð=Ð，AP AF =，∴BAF BAP BAF CAF Ð+Ð=Ð+Ð，∴60FAP BAC Ð=Ð=°，∴AFP V 是等边三角形，∴PF AP =，∴PA PB PF CF PC +=+=，即PA PB PC +=．【点睛】本题考查等边三角形的判定与性质，全等三角形的判定与性质，熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键．例2．（2023·湖南·长沙市八年级阶段练习）如图1，在Rt △ABC 中，∠B ＝90°，AB ＝BC ＝4，点D ，E 分别为边AB ，BC 上的中点，且BD ＝BE ．(1)如图2，将△BDE 绕点B 逆时针旋转任意角度α，连接AD ，EC ，则线段EC 与AD 的关系是 ；(2)如图3，DE ∥BC ，连接AE ，判断△EAC 的形状，并求出EC 的长；(3)继续旋转△BDE ，当∠AEC ＝90°时，请直接写出EC 的长．例3．（2023·黑龙江·虎林市九年级期末）已知Rt △ABC 中，AC =BC ，∠ACB ＝90°，F 为AB 边的中点，且DF =EF ，∠DFE ＝90°，D 是BC 上一个动点．如图1，当D 与C 重合时，易证：CD 2＋DB 2＝2DF 2；（1）当D 不与C 、B 重合时，如图2，CD 、DB 、DF 有怎样的数量关系，请直接写出你的猜想，不需证明．（2）当D 在BC 的延长线上时，如图3，CD 、DB 、DF 有怎样的数量关系，请写出你的猜想，并加以证明．【答案】（1）CD 2+DB 2=2DF 2 ；（2）CD 2+DB 2=2DF 2，证明见解析【分析】（1）由已知得222DE DF =，连接CF ，BE ，证明CDF BEF D @D 得CD =BE ，再证明BDE D 为直角三角形，由勾股定理可得结论；（2）连接CF ，BE ，证明CDF BEF D @D 得CD =BE ，再证明BDE D 为直角三角形，由勾股定理可得结论．【详解】解：（1）CD 2+DB 2=2DF 2证明：∵DF =EF ，∠DFE ＝90°，∴222DF EF DE += ∴222DE DF = 连接CF ，BE ，如图∵△ABC 是等腰直角三角形，F 为斜边AB 的中点∴CF BF =，CF AB ^，即90CFB Ð=° ∴45FCB FBC Ð=Ð=°，90CFD DFB Ð+Ð=°又90DFB EFB Ð+Ð=° ∴CFD EFB Ð=Ð在CFD D 和BFE D 中CF BF CFD BFE DF EF =ìïÐ=Ðíï=î∴CFD D @BFED ∴CD BE =，45EBF FCB Ð=Ð=° ∴454590DBF EBF Ð+Ð=°+°=° ∴222DB BE DE +=∵CD BE =，222DE DF =∴CD 2+DB 2=2DF 2 ；（2）CD 2+DB 2=2DF 2 证明：连接CF 、BE∵CF =BF ，DF =EF 又∵∠DFC +∠CFE =∠EFB +∠CFB=90°∴∠DFC =∠EFB ∴△DFC ≌△EFB ∴CD =BE ，∠DCF =∠EBF =135°∵∠EBD =∠EBF －∠FBD =135°－45°=90° 在Rt △DBE 中，BE 2+DB 2=DE 2∵ DE 2=2DF 2 ∴ CD 2+DB 2=2DF 2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键，学会添加常用辅助线，构造全等三角形解决问题．例4．（2022·青海·中考真题）两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，则形成一组全等的三角形，把具有这个规律的图形称为“手拉手”图形.(1)问题发现：如图1，若ABC V 和ADE V 是顶角相等的等腰三角形，BC ，DE 分别是底边.求证：BD CE =；(2)解决问题：如图2，若ACB △和DCE V 均为等腰直角三角形，90ACB DCE Ð=Ð=°，点A ，D ，E 在同一条直线上，CM 为DCE V 中DE 边上的高，连接BE ，请判断∠AEB 的度数及线段CM ，AE ，BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE Ð=°；2AE AD DE BE CM=+=+【分析】（1）先判断出∠BAD =∠CAE ，进而利用SAS 判断出△BAD ≌△CAE ，即可得出结论；（2）同（1）的方法判断出△BAD ≌△CAE ，得出AD =BE ，∠ADC =∠BEC ，最后用角的差，即可得出结论．【解析】(1)证明：∵ABC V 和ADE V 是顶角相等的等腰三角形，∴AB AC =，AD AE =，BAC DAE Ð=Ð，∴BAC CAD DAE CAD Ð-Ð=Ð-Ð，∴BAD CAE Ð=Ð．在BAD V 和CAE V 中，AB AC BAD CAE AD AE =ìïÐ=Ðíï=î，∴()BAD CAE SAS ≌△△，∴BD CE =．(2)解：90AEB =°∠，2AE BE CM =+，理由如下：由（1）的方法得，≌ACD BCE V V ，∴AD BE =，ADC BEC ÐÐ=，∵CDE △是等腰直角三角形，∴45CDE CED Ð=Ð=°，∴180135ADC CDE Ð=°-Ð=°，∴135BEC ADC Ð=Ð=°，∴1354590AEB BEC CED Ð=Ð-Ð=°-°=°．∵CD CE =，CM DE ^，∴DM ME =．∵90DCE Ð=°，∴DM ME CM ==，∴2DE CM =．∴2AE AD DE BE CM =+=+．【点睛】此题是三角形综合题，主要考查了全等三角形的判定和性质，等腰三角形，等边三角形，等腰直角三角形的性质，判断出△ACD ≌△BCE 是解本题的关键．3）15°模型2.半角模型【模型解读】半角模型概念：过多边形一个顶点作两条射线，使这两条射线夹角等于该顶角一半思想方法：通过旋转构造全等三角形，实现线段的转化1）正方形半角模型条件：四边形ABCD是正方形，∠ECF=45°；结论：①△BCE≌△DCG；②△CEF≌△CGF；③EF＝BE＋DF；④D AEF的周长=2AB；⑤CE、CF分别平分∠BEF和∠EFD。

半角模型十五个结论及证明《探索半角模型的十五个结论及证明》嗨，大家好！今天我要和大家一起探索一个超有趣的数学知识——半角模型的十五个结论及证明。

这就像是一场奇妙的数学冒险，跟我来呀！一、什么是半角模型呢？半角模型呀，就像是一个神秘的数学宝藏，藏在各种几何图形里。

想象一下，我们有一个正方形或者等腰直角三角形，然后在这个图形里出现了一个角，这个角是另外一个大角的一半，这就形成了半角模型。

比如说，在正方形里，一个角是45度，它就是直角90度的一半呢。

这时候啊，就会有好多神奇的结论冒出来。

二、结论一：线段相等我给大家举个例子哈。

在正方形ABCD中，∠EAF = 45度（E、F分别在BC、CD 上）。

我们能发现BE + DF = EF。

这是为啥呢？我们可以把△ADF绕着点A顺时针旋转90度，这样AD就和AB重合了。

旋转后的点F变成了F'。

那这个时候呀，我们就会发现△AEF和△AEF'是全等的。

为啥呢？因为AF = AF'，∠EAF = ∠EAF' = 45度，AE是公共边啊。

就像两个一模一样的小积木，那EF就等于EF'了，而EF'就是BE + DF呀。

你们说神奇不神奇？这就好比是把分散的力量集中起来了，原本分开的BE和DF，通过旋转这个魔法，就变成了和EF相等的线段。

三、结论二：三角形面积关系还有一个有趣的结论呢。

三角形AEF的面积等于三角形ABE的面积加上三角形ADF的面积。

这又怎么理解呢？我们刚刚把△ADF旋转到了△ABF'的位置。

那三角形AEF的面积就等于三角形AEF'的面积啦。

而三角形AEF'的面积就是三角形ABE的面积加上三角形ABF'（也就是原来的三角形ADF）的面积。

这就好像是把两个小地块合并起来就等于一个大地块的面积一样。

四、结论三：角平分线如果我们延长CB到G，使得BG = DF，连接AG。

我们会发现AG是∠EAG的角平分线呢。

专题07正方形基本型——半角模型【模型解读】知一推四：如图，ABCD 为正方形，E,F 分别是BC,DC 边上的点，母题：如图，ABCD 为正方形，E,F 分别是BC,DC 边上的点，∠EAF=45°，AG ⊥EF （2）DN ²+BM ²=MN ²（3）∠MGN=90°AA E 平分∠BEF BE +DF =EF∠EAF =45°作AH ⊥EF ，AH=AB AF 平分∠DFE⑤④③②①①DE+BF=EF ②BG 2+HD 2=GH 2③△AGD ∽△HGA ∽△HAB ：2子母型，1共享型 ④S ABCD =BH·DG⑤AH=HF ，AH ⊥HF ；AG=GE ，AG ⊥GE ⑥△AGH ∽△AEF （用全等导角） ⑦22==FC HD EF GH（4）证：①²•AM MN MD =；②²•AN NM NB =（5）证：△AMN 与△AFE 相似，并求出相似比（6）若BE=2,DF=3，①求AG ，②求MN 的值（7）①证明：AN=EN,②证明：AM ⊥MFFFF（8）证明BN•DM=S ABCD（9）证明NDEC（10）求BMFCFFFF【模型实例】1．如图，正方形ABCD 边长为6，E 是BC 的中点，连接AE ，以AE 为边在正方形内部作45EAF ∠=︒，边AF 交CD 于F ，连接EF ．则下列说法正确的有( ) ①30EAB ∠=︒；②BE DF EF +=；③tan 3AFE ∠=；④6CEF S ∆=．A ．①②③B ．②④C ．①④D ．②③④2．如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，AE AF =，AC 与EF 相交于点G ．下列结论：①AC 垂直平分EF ；②BE DF EF +=；③当15DAF ∠=︒时，AEF ∆为等边三角形；④当60EAF ∠=︒时，AEB AEF ∠=∠．其中正确的结论是( )A ．①③B ．②④C ．①③④D ．②③④3．如图，正方形ABCD 中，点E 、F 分别是BC 、CD 上的动点（不与点B ，C ，D 重合），且45EAF ∠=︒，AE 、AF 与对角线BD 分别相交于点G 、H ，连接EH 、EF ，则下列结论：①ABH GAH ∆∆∽；②ABG HEG ∆∆∽；③AE =；④EH AF ⊥；⑤EF BE DF =+ 其中正确的有( )A ．2B ．3C ．4D ．54．如图，正方形ABCD 的对角线相交于点O ，点M ，N 分别是边BC ，CD 上的动点（不与点B ，C ，D 重合），AM ，AN 分别交BD 于E ，F 两点，且45MAN ∠=︒，则下列结论：①MN BM DN =+；②AEF BEM ∆∆∽；③AF AM =；④FMC ∆是等腰三角形．其中正确的是 ．（填写正确序号）5．如图，点M 、N 分别是正方形ABCD 的边BC 、CD 上的两个动点，在运动过程中保持45MAN ∠=︒，AM 、AN 分别与对角线BD 交于点E 、F ，连接EN 、FM 相交于点O ，以下结论：①MN BM DN =+；②222BE DF EF +=；③2BC BF DE =⋅；④OM =，一定成立的是( )A ．①②③B ．①②④C ．②③④D ．①②③④6．如图，正方形ABCD 的对角线相交于点O ，点M ，N 分别是边BC ，CD 上的动点（不与点B ，C ，D 重合），AM ，AN 分别交BD 于E ，F 两点，且45MAN ∠=︒，则下列结论：①MN BM DN =+；②AEF BEM ∆∆∽；③2AF AM =；④FMC ∆是等腰三角形．其中正确的有( )A ．1个B ．2个C ．3个D ．4个专题04正方形基本型【模型解读】①DE+BF=EF②BG2+HD2=GH2③△AGD∽△HGA∽△HAB：2子母型，1共享型④S ABCD=BH·DG⑤AH=HF，AH⊥HF；AG=GE，AG⊥GE⑥△AGH∽△AEF（用全等导角）⑦22==FCHDEFGH知一推四：如图，ABCD 为正方形，E,F 分别是BC,DC 边上的点，BADFA E 平分∠BEF BE +DF =EF∠EAF =45°作AH ⊥EF ，AH=AB AF 平分∠DFE⑤④③②①母题：如图，ABCD 为正方形，E,F 分别是BC,DC 边上的点，∠EAF=45°，AG ⊥EF （2）DN ²+BM ²=MN ²【简证】旋转△AND ，可得'BN DN =且∠N’BM=90°，由勾股定理可知222''N M N B BM =+易证△绿≌△蓝，可知'N MMN =,从而得证ADADADFF（3）∠MGN=90°【简证】两组全等可得2个45°，从而得证（4）证：①²•AM MN MD =；②²•AN NM NB =FFFF【①简证】子母型相似【②简证】子母型相似（5）证：△AMN 与△AFE 相似，并求出相似比【简证】导角得相似，对应边上的高之比等于相似比FFFF（6）若BE=2,DF=3，①求AG ，②求MN 的值【① 简证】如图，设EC x =，则有22²154x x x +-=⇒=（），∴AG=AB=6【②简证】MN AH AMN AFE MN EF AG⇒==⇒==△∽△F x-13F相似比：AH AG AH AB ∠1=∠2=∠3（7）①证明：AN=EN,②证明：AM ⊥MF【① 简证】两次相似：△AMN ∽△BME ⇒△BMA ∽△EMN ；或者四点共圆【② 简证】同上3FFFF（8）证明BN •DM=S ABCD【简证】∠1=45°+∠2=∠BAN ⇒△BAN ∽△DMA ⇒BN •DM=AB •AD（9）证明ND EC（10）求BMFC【（9）简证】旋转相似FFFFF∣【（10）简证】旋转相似∣【模型实例】1．如图，正方形ABCD 边长为6，E 是BC 的中点，连接AE ，以AE 为边在正方形内部作45EAF ∠=︒，边AF 交CD 于F ，连接EF ．则下列说法正确的有( )①30EAB ∠=︒；②BE DF EF +=；③tan 3AFE ∠=；④6CEF S ∆=．A ．①②③B ．②④C ．①④D ．②③④【解答】解：延长CB 到G ，使BG DF =，连接AG ．如图所示： 四边形ABCD 是正方形，AB AD ∴=，90ABE D ∠=∠=︒，90ABG D ∴∠=︒=∠，在ABG ∆和ADF ∆中，FFFFAB AD ABG D BG DF =⎧⎪∠=∠⎨⎪=⎩， ()ABG ADF SAS ∴∆≅∆， AG AF ∴=，12∠=∠，又45EAF ∠=︒，90DAB ∠=︒， 2345∴∠+∠=︒， 1345∴∠+∠=︒， 45GAE EAF ∴∠=∠=︒．在AEG ∆和AEF ∆中， AG AF GAE EAF AE AE =⎧⎪∠=∠⎨⎪=⎩， ()AEG AEF SAS ∴∆≅∆， GE EF ∴=，GE BG BE =+，DF BG =，EF DF BE ∴=+，故②正确，3BE EC ==，6AB =， 1tan 32BE AB ∴∠==， 330∴∠≠︒，故①错误，设DF x =，则3EF x =+，在Rt EFC ∆中，222EF CF EC =+，222(3)3(6)x x ∴+=+-， 2x ∴=， 2DF BG ∴==，tan tan 3ABAFE G BG∴∠===，故③正确， 1134622CEF S CE CF ∆∴=⋅⋅=⨯⨯=，故④正确． 故选：D ．2．如图，在正方形ABCD中，点E，F分别在BC，CD上，AE AF=，AC与EF相交于点G．下列结论：①AC垂直平分EF；②BE DF EF∆为+=；③当15DAF∠=︒时，AEF等边三角形；④当60∠=∠．其中正确的结论是()∠=︒时，AEB AEFEAFA．①③B．②④C．①③④D．②③④【解答】解：四边形ABCD是正方形，∠=∠=︒，ACD ACB∠=∠=︒，45AB AD BC CD∴===，90B D=，AE AFAB AD=，∴∆≅∆，Rt ABE Rt ADF(HL)∴=，BE DF∴=，CE CF又45∠=∠=︒，ACD ACBAC∴垂直平分EF，故①正确；BCD∠=︒，AC垂直平分EF，=，90CE CF∴=，EG GF当AE平分BAC+=，故②错误；=，即BE DF EF∠时，BE EG∆≅∆，Rt ABE Rt ADF∴∠=∠=︒，DAF BAE15∴∠=︒，60EAF又AE AF=，∴∆是等边三角形，故③正确；AEF=，60AE AF∠=︒，EAF∴∆是等边三角形，AEFAEF∴∠=︒，60∠=︒，∠=︒，30CAEBAC45∴∠=︒，15BAE75AEB AEF ∴∠=︒≠∠，故④错误；故选：A ．3．如图，正方形ABCD 中，点E 、F 分别是BC 、CD 上的动点（不与点B ，C ，D 重合），且45EAF ∠=︒，AE 、AF 与对角线BD 分别相交于点G 、H ，连接EH 、EF ，则下列结论：①ABH GAH ∆∆∽；②ABG HEG ∆∆∽；③AE =；④EH AF ⊥；⑤EF BE DF =+ 其中正确的有( )A ．2B ．3C ．4D ．5【解答】解：在正方形ABCD 中， 45ABG ∴∠=︒，45AGH ABG BAG BAG ∴∠=∠+∠=︒+∠，45EAF ∠=︒， 45BAH BAG ∴∠=∠+︒， BAH AGH ∴∠=∠， AHG BHA ∠=∠，ABH GAH ∴∆∆∽，故①正确； 45EAF DBC ∠=∠=︒，A ∴，B ，E ，H 四点共圆，ABG GEH ∴∠=∠，BAG EHG ∠=∠， ABG HEG ∴∆∆∽；故②正确； 45AEH EAH ∠=∠=︒，AEH ∴∆是等腰直角三角形，90AHE ∴∠=︒，AE ，EH AF ∴⊥；故③④正确；将ADF ∆绕点A 顺时针旋转90︒得到ABM ∆，此时AB 与AD 重合，由旋转可得AB AD =，BM DF =，12∠=∠，90ABM D ∠=∠=︒，AM AF =，9090180ABM ABE ∴∠+∠=︒+︒=︒，因此，点M ，B ，E 在同一条直线上． 45EAF ∠=︒，23904545BAD EAE ∴∠+∠=∠-∠=︒-︒=︒．12∠=∠，1345∴∠+∠=︒．即MAE FAE ∠=∠．在AME ∆与AFE ∆中AM AF MAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩，AME AFE ∴∆≅∆． ME EF ∴=，故EF BE DF =+，故⑤正确， 故选：D ．4．如图，正方形ABCD 的对角线相交于点O ，点M ，N 分别是边BC ，CD 上的动点（不与点B ，C ，D 重合），AM ，AN 分别交BD 于E ，F 两点，且45MAN ∠=︒，则下列结论：①MN BM DN =+；②AEF BEM ∆∆∽；③AF AM ；④FMC ∆是等腰三角形．其中正确的是 ①②③④ ．（填写正确序号）【解答】解：将ABM ∆绕点A 逆时针旋转90︒至ADM ∆'，45M AN DAN MAB ∠'=∠+∠=︒，AM AM '=，BM DM ='，45M AN MAN ∠'=∠=︒，AN AN =， AMN ∴∆≅△()AM N SAS ''， MN NM ∴='，M N M D DN BM DN ∴'='+=+， MN BM DN ∴=+；故①正确； 135FDM ∠'=︒，45M AN ∠'=︒， 180M AFD ∴∠'+∠=︒， 180AFE AFD ∠+∠=︒，AFE M ∴∠=∠'， AMB M ∠=∠'， AMB AFE ∴∠=∠，45EAF EBM ∠=∠=︒，AEF BEM ∴∆∆∽，故②正确；∴AE EF BE EM =，即AE BEEF EM=， AEB MEF ∠=∠， AEB FEM ∴∆∆∽，45EMF ABE ∴∠=∠=︒，AFM ∴∆是等腰直角三角形，∴AF AM =；故③正确； 在ADF ∆与CDF ∆中， 45AD DC ADF CDF DF DF =⎧⎪∠=∠=︒⎨⎪=⎩， ()ADF CDF SAS ∴∆≅∆， AF CF ∴=，AF MF =，FM FC ∴=，FMC ∴∆是等腰三角形，故④正确；故答案为：①②③④．5．如图，点M 、N 分别是正方形ABCD 的边BC 、CD 上的两个动点，在运动过程中保持45MAN ∠=︒，AM 、AN 分别与对角线BD 交于点E 、F ，连接EN 、FM 相交于点O ，以下结论：①MN BM DN =+；②222BE DF EF +=；③2BC BF DE =⋅；④OM =，一定成立的是( )A ．①②③B ．①②④C ．②③④D ．①②③④【解答】解：将ABM ∆绕点A 逆时针旋转90︒，得到ADM ∆'，将ADF ∆绕点A 顺时针旋转90︒，得到ABD '∆，AM AM '∴=，BM DM '=，BAM DAM '∠=∠，90MAM '∠=︒，90ABM ADM '∠=∠=︒， 180ADM ADC '∴∠+∠=︒，∴点M '在直线CD 上，45MAN ∠=︒，45DAN MAB DAN DAM M AN ''∴∠+∠=︒=∠+∠=∠， 45M AN MAN ∴∠'=∠=︒，又AN AN =，AM AM '=，AMN ∴∆≅△()AM N SAS '， MN NM ∴='，M N M D DN BM DN ∴'='+=+， MN BM DN ∴=+；故①正确；将ADF ∆绕点A 顺时针旋转90︒，得到ABD '∆，AF AD '∴=，DF D B '=，45ADF ABD '∠=∠=︒，DAF BAD '∠=∠，90D BE '∴∠=︒， 45MAN ∠=︒，45BAE DAF BAD BAE D AE ''∴∠+∠=︒=∠+∠=∠，45D AE EAF '∴∠=∠=︒，又AE AE =，AF AD '=，()AEF AED SAS '∴∆≅∆，EF D E '∴=，222D E BE D B ''=+，222BE DF EF ∴+=；故②正确；45BAF BAE EAF BAE ∠=∠+∠=∠+︒，45AEF BAE ABE BAE ∠=∠+∠=︒+∠， BAF AEF ∴∠=∠，又45ABF ADE ∠=∠=︒，DAE BFA ∴∆∆∽， ∴DE AD AB BF=， 又AB AD BC ==， 2BC DE DF ∴=⋅，故③正确；45FBM FAM ∠=∠=︒，∴点A ，点B ，点M ，点F 四点共圆，90ABM AFM ∴∠=∠=︒，45AMF ABF ∠=∠=︒，BAM BFM ∠=∠， 同理可求90AEN ∠=︒，DAN DEN ∠=∠，45EOM EMO ∴∠=︒=∠，EO EM ∴=，MO ∴=，BAM DAN ∠≠∠，BFM DEN ∴∠≠∠，EO FO ∴≠，OM ∴≠，故④错误，故选：A ．6．如图，正方形ABCD 的对角线相交于点O ，点M ，N 分别是边BC ，CD 上的动点（不与点B ，C ，D 重合），AM ，AN 分别交BD 于E ，F 两点，且45MAN ∠=︒，则下列结论：①MN BM DN =+；②AEF BEM ∆∆∽；③AF AM ；④FMC ∆是等腰三角形．其中正确的有( )A ．1个B ．2个C ．3个D ．4个【解答】解：将ABM ∆绕点A 逆时针旋转90︒至ADM ∆'，45M AN DAN MAB ∠'=∠+∠=︒，AM AM '=，BM DM ='，45M AN MAN ∠'=∠=︒，AN AN =，AMN ∴∆≅△()AM N SAS ''，MN NM ∴='，M N M D DN BM DN ∴'='+=+，MN BM DN ∴=+；故①正确；135FDM ∠'=︒，45M AN ∠'=︒，180M AFD ∴∠'+∠=︒，180AFE AFD ∠+∠=︒，AFE M ∴∠=∠'，AMB M ∠=∠'，AMB AFE ∴∠=∠，45EAF EBM ∠=∠=︒，AEF BEM ∴∆∆∽，故②正确； ∴AE EFBE EM =，即AEBEEF EM =，AEB MEF ∠=∠，AEB FEM ∴∆∆∽，45EMF ABE ∴∠=∠=︒，AFM ∴∆是等腰直角三角形，∴AF AM =；故③正确；在ADF ∆与CDF ∆中，45AD CDADF CDF DF DF=⎧⎪∠=∠=︒⎨⎪=⎩，()ADF CDF SAS ∴∆≅∆，AF CF ∴=，=，AF MF∴=，FM FC∴∆是等腰三角形，故④正确；FMC故选：D．。

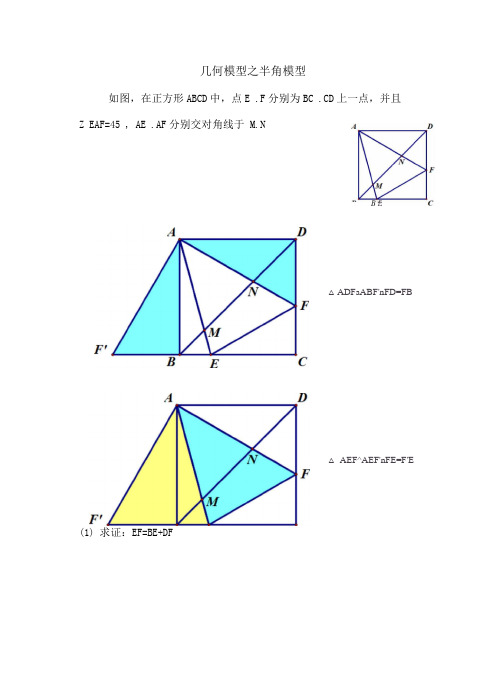
几何模型之半角模型如图，在正方形ABCD中，点E .F分别为BC .CD上一点，并且Z EAF=45 , AE .AF分别交对角线于M.N(1) 求证：EF=BE+DFB E△ADFaABF'nFD=FB △ AEF^AEF'nFE=F'E2—2一 2MN 2 = BM DN 2A ADN 三△ ABN'nDN=BN‘ZDSA = 45,00，匕MN —45.00”=NMBN'=90。

BMgNFM ^BM^DN^MN 2⑵求证:AAMN-AAMN(3)求证：Z AEBW AEFW ANMZAFDW AEFW AMNA ADF^ABF' n ZAFD=ZAF r B△AEF^AEF nZEAE2DBZANM=ZDNF=>ZAMN=ZAFD同理ZANM=AEB(4)2AM 2 = BM 2 DM 22AN2 = BN2 DN2M f△ABM^ADXTnBM=DM'A AMM，是等腰RTAA MAM 是RT A =>MD2 -Mb=MM t2得证：2AM?-BM2 +DM;同理二………E fA ABE三△ ADE %AE=AE E fAE=AE r ZEAE^90°ZEAN=ZNAE r-45°得证:「……△ADF^ABF'nAF二AF B C.... :买割 -HN=Na^NHa^*3NVV 朋辑风(S)由副」ci + ve = IAICI 寸 勺日+va=NS # (Z )应ff■3v=mg .aovv^aav v3 Sa 、、匠■ M△ADF^ABF'nDF=AF'借用(5)的结论AAMF =A MDF =>MD=MF f得证: .....B C(8) CE =、、2DN,CF =、.2BMA AXE-A ANE=>AE,=V2N,E=BEF△ATFSAQMnAQ 峪TF=DF(9) EF = ,2MN结论(6)AAEF-A ANM=>EF=V2MN(10)作GE_ BC,N是DG中点AABE 三AEB'E—BE，=BEBC'=B'E‘A ADN-A GNE'nDN=GN(11)作FH ± DB ,BM=MHA ADF=4 ABF'nA 是等腰RTAA MHF 三△(12)作 Pd BD NP=1/2BDA DF AEGB 是等®RTA PE1B nBP=PG1nPN= 一 BD2在（10）的结论上A ADN 三 A GNE'nDN=GN(13)FQ ± BD MQ=1/2BD在(11)的结论上A MHFMBF'nHM=MB△HFD是等腰RTA QF_LBD=HQ=QD1=>QM- —BD(13)4AMN-AAEFAF=^2AM。

半角模型课程名称授课教师年级日期学科时段数学1掌握半角模型的模型特点，学会辨认半角模型2学会使用半角模型的方法进行解题教学目标3学会找出隐藏的半角模型，并能够正确解答课首沟通上次课的内容是什么？现在的学校进度到哪里了？学校最近有测验吗？知识导图课首小测书面测试1. 如图，在正方形ABCD的外侧，作等边△ABE，则∠BED为多少度？2.如图，已知正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°求证：EF＝BE+DF知识梳理模型概述：定义：我们习惯把过等腰三角形顶角的顶点引两条射线，使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。

常见的图形为正方形，正三角形，等腰直角三角形等，解题思路一般是将半角两边的三角形通过旋转到一边合并形成新的三角形，从而进行等量代换，然后证明与半角形成的三角形全等，再通过全等的性质得出线段之间的数量关系，从而解决问题。

导学一正方形内含半角知识点讲解 1 正方形内含半角思想方法：通过旋转变换构造全等三角形，实现线段的转化。

例题1.如图，在正方形ABCD钟，E,F分别是BC，CD边上的点，∠EAF=45°，证明以下结论：(1)EF=BE+DF(2)△CEF的周长是正方形边长的2倍。

(3)FA平分∠DFE,EA平分∠BEF；(4)S△AEF=S△AEB+S△AFD2.如图，在正方形ABCD 中，AB ＝1，点E ，F 分别在边BC 和CD 上，AE ＝AF ，∠EAF ＝60°，则CF 的长是________.3. 如图，在正方形ABCD 中，AB ＝1，E ，F 分别是边BC ，CD 上的点，连接EF 、AE 、AF ，过A 作AH ⊥EF 于点H ．若EF ＝BE+DF ，那么下列结论：①AE 平分∠BEF ；②FH ＝FD ；③∠EAF ＝45°；④S＝S +S△EAF △ABE △ADF ；⑤△CEF 的周长为2． 其中正确结论的序号是__________ 我爱展示我爱展示题1.如图，在正方形ABCD 中，E 、F 分别是边BC 、CD 上的点，∠EAF ＝45°，正方形ABCD 的边长为3，则△ECF 的周长为 ．2. 如图，正方形ABCD中，AB＝1，点E、F分别是边BC、CD上的两点，∠EAF＝45°，AG⊥EF于点G，连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH．以下结论正确的是__________ ．2 2 2 2 2 2①AG＝1；②△CEF的周长是定值，定值是2；③DF +BE ＝EF ；④DN +BM ＝MN ．3. 如图，正方形ABCD的边长为4，点E是CD的中点，AF平分∠BAE交BC于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为_____ ．导学二等腰三角形内含半角例题1. （1）如图1，已知△ABC，∠ACB＝90°，AC＝BC，点E、F在直线AB上，∠ECF＝∠B，①△ACF与△BEC的关系为．②设△ABC的面积为S，求证：AF•BE＝2S．（2）如图2，将（1）中的∠ACB＝90°改为∠ACB＝α°，求证：（3）如图3，在（2）中的条件不变的情况下，（2）中的结论是否成立？（直接写出结论，不用说明理由）2. （1）如图1，点E、F分别是正方形ABCD的边BC、CD上的点，∠EAF＝45°，连接EF，2 2 2则EF、BE、FD之间的数量关系是：EF＝BE+FD．连结BD，交AE、AF于点M、N，且MN、BM、DN满足MN ＝BM +DN ，请证明这个等量关系；（2）在△ABC中，AB＝AC，点D、E分别为BC边上的两点．①如图2，当∠BAC＝60°，∠DAE＝30°时，BD、DE、EC应满足的等量关系是_____________ ；②如图3，当∠BAC＝α，（0°＜α＜90°），∠DAE＝时，BD、DE、EC应满足的等量关系是___________ ．2 2[参考：sin α+cos α＝1】3. D为等边△ABC外一点，且BD＝CD，∠BDC＝120°，点M，N分别在AB，AC上，若BM+CN＝MN，求证：（1）∠MDN＝60°；（2）作出△DMN的高DH，并证明DH＝BD．我爱展示我爱展示题1. 【发现证明】（1）如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，试判断BE、EF、FD之间的数量关系．小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF＝BE+FD，请你利用图1证明上述结论．【类比引申】（2）如图2，点E、F分别在正方形ABCD的边CB、CD的延长线上，∠EAF＝45°，连接EF，请直接写出EF、BE、DF之间的数量关系，不需证明；【联想拓展】（3）如图3，如图，∠BAC＝90°，AB＝AC，点E、F在边BC上，且∠EAF＝45°，若BE＝1，CF＝2，求EF的长．2. 在等边△ABC的两边AB、AC所在直线上分别有两点M、N，D为△ABC外一点，且∠MDN＝60°，∠BDC＝120°，BD＝DC．探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系．（1）如图1，当点M、N边AB、AC上，且DM＝DN时，BM、NC、MN之间的数量关系是__________ ；此时＝__________ ；（2）如图2，点M、N在边AB、AC上，且当DM≠DN时，猜想（ I）问的两个结论还成立吗？若成立请直接写出你的结论；若不成立请说明理由．（3）如图3，当M、N分别在边AB、CA的延长线上时，探索BM、NC、MN之间的数量关系如何？并给出证明．导学三半角模型综合题例题1. 如图，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于M、N，连接EN、EF，有以下结论：正确的序号是________.2. 探究：（1）如图1，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，试判断BE、DF与EF三条线段之间的数量关系，直接写出判断结果：_______ ；（2）如图2，若把（1）问中的条件变为“在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD”，则（1）问中的结论是否仍然成立？若成立，请给出证明，若不成立，请说明理由；（3）在（2）问中，若将△AEF绕点A逆时针旋转，当点分别E、F运动到BC、CD延长线上时，如图3所示，其它条件不变，则（1）问中的结论是否发生变化？若变化，请给出结论并予以证明．我爱展示我爱展示题1.如图，边长为的正方形ABCD的对角线AC与BD交于点O，将正方形ABCD沿直线DF折叠，点C落在对角线BD上的点E处，折痕DF交AC于点M，则OM＝_________.2. （1）如图1，在正方形ABCD中，E、F分别是边BC、CD上的点，且∠EAF＝45°，把△ADF绕着点A顺时针旋转90°得到△ABG，请直接写出图中所有的全等三角形；（2）在四边形ABCD中，AB＝AD，∠B＝∠D＝90°．①如图2，若E、F分别是边BC、CD上的点，且2∠EAF＝∠BAD，求证：EF＝BE+DF；②若E、F分别是边BC、CD延长线上的点，且2∠EAF＝∠BAD，①中的结论是否仍然成立？请说明理由．限时考场模拟1.正方形ABCD中，E，F分别是边BC，CD上的点，且∠EAF＝45°，将△ABE绕点A逆时针旋转90°，得到△ADG．求证：EF＝BE+DF．2.如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD∥AB，∠ABC的平分线BD交AC于点E，DE＝．3. 如图，在△ABC中，AC：BC：AB＝5：12：13，⊙O在△ABC内自由移动，若⊙O的半径为1，且圆心O在△ABC内所能到达的区域的面积为，则△ABC的周长为．自主学习1.已知，如图，在RT△ABC中，∠ACB=90°，AC=BC,点D,E在斜边AB上，且∠DCE=45°，求证：线段DE,AD,BE中能构成一个直角三角形。

半角模型应用比较广泛：理解半角模型的定义，掌握正方形背景中半角模型的模型的应用，掌握等腰直角三角形背景中半角模型的应用尤为重要。

知识精讲：过等腰三角形顶点两条射线，使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。

常见的图形为正方形，正三角形，等腰直角三角形等，解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形，从而进行等量代换，然后证明与半角形成的三角形全等，再通过全等的性质得到线段之间的数量关系。

解题技巧：在图1中，△AEB由△AND旋转所得，可得△AEM≌△AMN，∴BM+DN=MN∠AMB=∠AMNAB=AH△CMN的周长等于正方形周长的一半在图2中将△ABC旋转至△BEF，易得△BED≌△BCD同理得到边角之间的关系；总之：半角模型（题中出现角度之间的半角关系）利用旋转——证全等——得到相关结论.题型讲解：1、正方形ABCD中，E是CD边上一点.将△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，如图1所示，观察可知：与DE相等的线段是______,∠AFB=_______.如图2，正方形ABCD中，P、Q分别是BC、CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ.2、如图，已知△ABC中，∠BAC=90°，AB=AC,D,E是BC边上的点，将△ABD绕点A旋转，得到△ACD′，当∠DAE=45°时，求证：DE=D′E；在（1）的条件下，猜想：BD2，DE2，CE2有怎样的数量关系？请写出，并说明理由.3、如图，E、F是正方形ABCD的边AD、CD上的点，连BE、EF、BF，BF平分∠EBC。

求证：BE=AE+CF4、正方形ABCD中，E,F分别是边BC,CD上的点，且∠EAF=45°，将△ABE绕点A逆时针旋转90°，得到△ADG，求证：EF=BE+DF.5、在等边△ABC的两边AB，AC所在直线上分别有两点M、N，D为△ABC外一点，且∠MDN=60°，∠BDC=120°，BD=DC.探究：当M、N分别在直线AB,AC上移动时，BM, NC,MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系，如图1，△ABC是周长为9的等边三角形，则△AMN的周长Q=_______如图2，当点M,N边AB,AC上，且DM=DN时，BM,NC,MN之间的数量关系是______;Q=_______L点M,N在边AB,AC上，且当DM≠DN时，猜想（2）问的两个结论还成立吗？写出你的猜想并加以证明.专项练习：如图，△ABC是正三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°的角，角的两边分别交于AB于M，交AC于N,连接MN,求证：MN=BM+CN.【解析】半角模型，先证旋转全等△DCN≌△DBQ，再证对称全等△DNM≌△DQM7、已知四边形ABCD中，AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°，∠MBN=60°，∠MBN 绕点B旋转，它的两边分别交AD,DC（或它们的延长线）于E,F当∠MBN绕B点旋转到AE=CF时，求证：△ABE≌△CBF当∠MBN绕点B旋转到AE≠CF时，如图2，猜想线段AE,CF,EF有怎样的数量关系，并证明你的猜想当∠MBN绕点B旋转到图三这种情况下，猜想线段AE,CF,EF有怎样的数量关系，并证明你的猜想.【解析】半角模型（1）SAS证全等即可（2）作∠EBQ=120°，或延长FC至点Q使得CQ=AE，证旋转和对称全等得到AE+CF=EF（3）在AM上取一点H使得AH=CF，证△BAH≌△BCF，△BFE≌△BHE可得AE=FC+EF8、如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.求证：CE=CF若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？【解析】（1）半角模型，证△CBE≌△CDF即可（2）成立，证完旋转全等（△CBE≌△CDF）再证对称全等（△CEG≌△CFG）即可9、E,F分别是正方形ABCD的边BC,CD上的点，且∠EAF=45°，AH⊥EF,H为垂足，求证：AH=AB.【解析】半角模型，延长EB至点M使得BM=DF，证△ADF≌ABM（旋转全等），再证△AFE≌△AME（对称全等）得AE平分∠FEM即可10、已知两个全等的等腰直角△ABC,△DEF，其中∠∠ACB=∠DFE=90°，E为AB中点，△DEF可绕顶点E旋转，线段DE，EF分别交线段CA,CB（或它们所在直线）于M,N如图1，当线段EF经过△ABC的顶点C时，点N与点C重合，线段DE交AC于M,求证：AM=MC如图2，当线段EF与线段BC边交于点N，线段DE与线段AC交于M点，连MN,EC,请探究AM,MN,CN之间的等量关系，并说明理由.如图3，当线段EF与BC延长线交于点N点，线段DE与线段AC交于M点，连MN,EC，请猜想AM,MN,CN之间的等量关系，不必说明理由.【解析】（1）CE是中垂线，∠FED=45°，所以EM是中垂线，则AM=MC（2）AM-CN=MN；过E作EG⊥EN交AC于点G，可证△AGE≌△CEN（AAS），再证△EGM≌△ENM（SAS）【半角模型，先证旋转全等，再证对称全等】（3）AM+CN=MN；过E作EH⊥EN交AC的延长线于点H，可证△AHE≌△CNE （AAS），再证△EHM≌△ENM（SAS）【半角模型，先证旋转全等，再证对称全等】答案：1、解析：∵△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF,∵DE=BF,∠AFB=∠AED.将△ADQ绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABE，如图2，则∠D=∠ABE=90°即点E,BP共线，∠EAQ=∠BAD=90°，AE=AQ,BE=DQ∵∠PAQ=45°∠PAE=45°∴∠PAQ=∠PAE在△APE和△APQ中AE=AQ∠PAE=∠PAQAP=AP△APE≌△APQ(SAS)∴PE=PQ而PE=PB+BE=PB+DQ∴DQ+BP=PQABD2、解析：因为△ABD绕点A旋转，得到△ACD′∴AD=AD′，∠DAD’=∠BAC=90°∵∠DAE=45°∴∠EAD’=∠DAD’-∠DAE=45°∴在△AED和△AED′中AE=AE∠EAD=∠AED’AD=AD’∴△AED≌△AED’∴DE=D’E由（1）得△AED≌△AED’，ED=ED’在△ABC中，AB=AC,∠BAC=90°∴∠B=∠ACB=45°∵△ABD绕点A旋转，得到△ACD’∴BD=CD’,∠B=∠ACD’=45°∴∠BCD’=∠ACB+∠ACD’=45°+45°=90°3、解析：将△CBF逆时针旋转90°得到△ABG,由旋转的性质可得AG=CF,∠G=∠BFC,∠ABG=∠CBF∵BF平分∠EBC,∴∠EBG=∠ABF=∠BFC∴∠G=∠EBG∴EG=EB∴BE=AE+CF.4、解析：如图，由题意得：△ABE≌△ADG∴∠BAE=∠DAG,AE=AG,BE=DG∴FG=BE+DF∴∠BAE+∠FAD=∠FAD+∠DAG∵∠EAF=45°，∠BAD=90°∴∠BAE+∠FAD=90°-45°，∴∠FAG=45°，∠EAF=∠FAG 在△EAF和△GAF中，AE=AG∠EAF=∠GAFAF=AF∴△EAF≌△GAF（SAS）∴EF=FG,而FG=BE+DF∴EF=BE+DF5、解析：（1）如图2，延长AC至E，使CE=BM,连接DE可得△MBD≌△ECD(SAS)∴DM=DE,∠BDM=∠CDE∴∠EDM=∠BDC-∠MDN=60°同理可得△MDN≌△EDN(SAS)∴MN=NE=NC+BM∵△AMN的周长Q=AM+AN+MN=AM+AN+(NV+BM)=(AM+BM)+(AN+NC)=AB+AC=2AB等边△ABC的周长L=3AB=9，AB=3，则Q=6（2）如图，BM,NC,MN之间的数量关系BM+NC=MN.此时QL =23（3）（2）中的结论仍然成立，证明参考（1）专项练习：1、【解析】半角模型，先证旋转全等△DCN≌△DBQ，再证对称全等△DNM≌△DQM2、【解析】半角模型（1）SAS证全等即可（2）作∠EBQ=120°，或延长FC至点Q使得CQ=AE，证旋转和对称全等得到AE+CF=EF（3）在AM上取一点H使得AH=CF，证△BAH≌△BCF，△BFE≌△BHE可得AE=FC+EF3、【解析】（1）半角模型，证△CBE≌△CDF即可（2）成立，证完旋转全等（△CBE≌△CDF）再证对称全等（△CEG≌△CFG）即可4、【解析】半角模型，延长EB至点M使得BM=DF，证△ADF≌ABM（旋转全等），再证△AFE≌△AME（对称全等）得AE平分∠FEM即可5、【解析】（1）CE是中垂线，∠FED=45°，所以EM是中垂线，则AM=MC（2）AM-CN=MN；过E作EG⊥EN交AC于点G，可证△AGE≌△CEN（AAS），再证△EGM≌△ENM（SAS）【半角模型，先证旋转全等，再证对称全等】（3）AM+CN=MN；过E作EH⊥EN交AC的延长线于点H，可证△AHE≌△CNE（AAS），再证△EHM≌△ENM（SAS）【半角模型，先证旋转全等，再证对称全等】。

并非把结论写全。

小结：（1）正方形与矩形，菱形，平行四边形的关系如上图（2）正方形的性质：①正方形对边平行。

②正方形四边相等。

③正方形四个角都是直角。

④正方形对角线相等，互相垂直平分，每条对角线平分一组对角。

典型例题精讲例1．如图，折叠正方形纸片ABCD，先折出折痕BD，再折叠使AD边与对角线BD重合，得折痕DG，使2AD ，求AG．【解析】：作GM⊥BD，垂足为M．由题意可知∠ADG=GDM ， 则△ADG ≌△MDG ． ∴DM=DA=2． AC=GM 又易知：GM=BM ．而BM=BD-DM=22-2=2（2-1）， ∴AG=BM=2（2-1）．例 2 ．如图，P 为正方形ABCD 内一点，10PA PB ==，并且P 点到CD 边的距离也等于10，求正方形ABCD 的面积【解析】：过P 作EF AB ⊥于F 交DC 于E ． 设PF x =，则10EF x =+，1(10)2BF x =+． 由222PB PF BF =+． 可得：222110(10)4x x =++． 故6x =．216256ABCD S ==．例 3. 如图，E、F分别为正方形ABCD的边BC、CD上的一点，AM EF⊥，•垂足为M，AM AB=+，为什么=，则有EF BE DF【解析】：要说明EF=BE+DF，只需说明BE=EM，DF=FM即可，而连结AE、AF．只要能说明△ABE≌△AME，△ADF≌△AMF即可．理由：连结AE、AF．由AB=AM，AB⊥BC，AM⊥EF，AE公用，∴△ABE≌△AME．∴BE=ME．同理可得，△ADF≌△AMF．∴DF=MF．∴EF=ME+MF=BE+DF．例4．如下图E、F分别在正方形ABCD的边BC、CD上，且45∠=，试说EAF︒明EF BE DF=+。

【解析】：将△ADF旋转到△ABC，则△ADF≌△ABG ∴AF=AG，∠ADF=∠BAG，DF=BG∵∠EAF=45°且四边形是正方形，∴∠ADF﹢∠BAE=45°∴∠GAB﹢∠BAE=45°即∠GAE=45°∴△AEF≌△AEG（SAS）∴EF=EG=EB﹢BG=EB﹢DF例5. 如图，在正方形ABCD的BC、CD边上取E、F两点，使45∠=，AG EFEAF=⊥于G. 求证：AG AB【解析】：欲证 AG=AB，就图形直观来看，应证Rt△ABE与Rt△AGE全等，但条件不够.∠EAF=45°怎么用呢显然∠1＋∠2=45°，若把它们拼在一起，问题就解决了.【证明】：把 △AFD 绕A 点旋转90°至△AHB.∵∠EAF=45°，∴∠1＋∠2=45°. ∵∠2=∠3，∴∠1＋∠3=45°. 又由旋转所得 AH=AF ，AE=AE. ∴ △AEF ≌△AEH.例6.(1) 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,90AOF ︒∠=.求证：BE CF =.(2) 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,90FOH ︒∠=,4EF =.求GH 的长.1.已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上，EF ,GH 交于点O ,90FOH ︒∠=,4EF =. 直接写出下列两题的答案：①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长；②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n 的代数式表示).【解析】(1) 证明：如图1，∵ 四边形ABCD 为正方形，∴ AB =BC ,∠ABC =∠BCD =90°， ∴ ∠EAB +∠AEB =90°. ∵ ∠EOB =∠AOF ＝90°,∴ ∠FBC +∠AEB =90°，∴ ∠EAB =∠FBC ， ∴ △ABE ≌△BCF ， ∴ BE =CF ．(2) 解：如图2,过点A作AM如图6，点A在线段BG上，四边形ABCD与DEFG 都是正方形，•其边长分别为3cm和5cm，则CDEcm．∆的面积为________2(6) (7)2．你可以依次剪6张正方形纸片，拼成如图7所示图形．•如果你所拼得的图形中正方形①的面积为1，且正方形⑥与正方形③的面积相等，•那么正方形⑤的面积为________．3.如图9，已知正方形ABCD的面积为35平方厘米，E、F分别为边AB、BC 上的点．AF、CE相交于G，并且ABF∆的面积∆的面积为14平方厘米，BCE为5平方厘米，•那么四边形BEGF的面积是________．4.如图，A、B、C三点在同一条直线上，2=。

专题04全等模型-半角模型全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就半角模型进行梳理及对应试题分析，方便掌握。

半角模型概念：过多边形一个顶点作两条射线，使这两条射线夹角等于该顶角一半。

思想方法：通过旋转（或截长补短）构造全等三角形，实现线段的转化。

解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形，从而进行等量代换，然后证明与半角形成的三角形全等，再通过全等的性质得到线段之间的数量关系。

半角模型（题中出现角度之间的半角关系）利用旋转——证全等——得到相关结论.模型1.半角模型（90°-45°型）【模型展示】1）正方形半角模型条件：四边形ABCD是正方形，∠ECF=45°；结论：①△BCE≌△DCG；②△CEF≌△CGF；③EF＝BE＋DF；④∆AEF的周长=2AB；⑤CE、CF分别平分∠BEF和∠EFD。

2）等腰直角三角形半角模型条件：∆ABC是等腰直角三角形，∠DAE=45°；结论：①△BAD≌△CAG；②△DAE≌△GAE；③∠ECG==90°；④DE2＝BD2＋EC2；例1．（2022·福建·龙岩九年级期中）（1）【发现证明】如图1，在正方形ABCD 中，点E ，F 分别是BC ，CD 边上的动点，且45EAF ∠=︒，求证：EF DF BE =+．小明发现，当把ABE △绕点A 顺时针旋转90°至ADG ，使AB 与AD 重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形ABCD 中，如果点E ，F 分别是CB ，DC 延长线上的动点，且45EAF ∠=︒，则（1）中的结论还成立吗？若不成立，请写出EF ，BE ，DF 之间的数量关系______（不要求证明）②如图3，如果点E ，F 分别是BC ，CD 延长线上的动点，且45EAF ∠=︒，则EF ，BE ，DF 之间的数量关系是_____（不要求证明）.（3）【联想拓展】如图1，若正方形ABCD 的边长为6，AE =AF 的长．例2．（2022·江苏·八年级专题练习）如图，△ABC ，△DEP 是两个全等的等腰直角三角形，∠BAC ＝∠PDE ＝90°．使△DEP 的顶点P 与△ABC 的顶点A 重合，PD ，PE 分别与BC 相交于点F 、G ，若BF ＝6，CG ＝4，则FG ＝_____．例3．（2022春·山东烟台·八年级校考期中）如图，正方形ABCD的边长为6，点E，F分别在边AB，BC上，若F是BC的中点，且∠EDF＝45°，则DE的长为_____．△绕点（分析：我们把ADF于是易证得：ADF≅直接应用：正方形ABCD(2)【变式练习】已知：如图、、之间的数量关系，并说明理由．写出BD DE CE模型2.半角模型（60°-30°型或120°-60°型）1）等边三角形半角模型（120°-60°型）条件：∆ABC是等边三角形，∆BDC是等腰三角形，且BD=CD，∠BDC=120°，∠EDF=60°；结论：①△BDE≌△CDG；②△EDF≌△GDF；③EF＝BE＋FC；④∆AEF的周长=2AB；⑤DE、DF分别平分∠BEF和∠EFC。

初中数学半角模型
在初中数学中，半角模型是一个非常重要的概念。

它是指一个角度的度数为45度，也就是说，这个角度是一个直角的一半。

半角模型在初中数学中的应用非常广泛，可以用来解决各种几何问题。

半角模型可以用来求解直角三角形的边长。

在一个直角三角形中，如果已知一个角度为45度，那么可以利用半角模型求出另外两个角度的度数，从而求出三角形的边长。

例如，如果已知一个直角三角形的一个角度为45度，另一个角度为30度，那么可以利用半角模型求出第三个角度的度数为90度，从而求出三角形的边长。

半角模型还可以用来求解正方形的对角线长度。

在一个正方形中，对角线的长度可以用勾股定理求解，但是如果已知一个角度为45度，那么可以利用半角模型求出正方形的对角线长度。

例如，如果已知一个正方形的一个角度为45度，那么可以利用半角模型求出正方形的对角线长度为边长的根号2倍。

半角模型还可以用来求解其他几何问题。

例如，在一个等腰直角三角形中，如果已知一个角度为45度，那么可以利用半角模型求出另一个角度的度数为45度，从而求出三角形的边长。

同样地，在一个菱形中，如果已知一个角度为45度，那么可以利用半角模型求出菱形的对角线长度为边长的根号2倍。

半角模型是初中数学中一个非常重要的概念，它可以用来解决各种
几何问题。

在学习初中数学时，我们应该认真掌握半角模型的概念和应用，以便更好地理解和应用数学知识。

几何图形之半角模型主题半角模型教学内容教学目标1.掌握正方形的定义，弄清正方形与平行四边形、菱形、矩形的关系。

2.掌握正方形的性质定理1和性质定理2。

3.正确运用正方形的性质解题。

4.通过四边形的从属关系渗透集合思想。

5.通过理解四种四边形内在联系，培养学生辩证观点。

知识结构正方形的性质因为正方形是特殊的平行四边形，还是特殊的矩形，特殊的菱形，所以它具有这些图形性质的综合，因此正方形有以下性质（由学生和老师一起总结）。

正方形性质定理1：正方形的四个角都是直角，四条边相等。

正方形性质定理2：正方形的两条对角线相等并且互相垂直平分，每一条对角线平分一组对角。

说明：定理2包括了平行四边形，矩形，菱形对角线的性质，一个题设同时有四个结论，这是该定理的特点，在应用时需要哪个结论就用哪个结论，并非把结论写全。

小结：（1）正方形与矩形，菱形，平行四边形的关系如上图（2）正方形的性质：①正方形对边平行。

②正方形四边相等。

③正方形四个角都是直角。

④正方形对角线相等，互相垂直平分，每条对角线平分一组对角。

典型例题精讲例1．如图，折叠正方形纸片ABCD ，先折出折痕BD ，再折叠使AD 边与对角线BD 重合，得折痕DG ，使2AD =，求AG ．【解析】：作GM ⊥BD ，垂足为M ． 由题意可知∠ADG=GDM ， 则△ADG ≌△MDG ． ∴DM=DA=2． AC=GM 又易知：GM=BM ．而BM=BD-DM=22-2=2（2-1）， ∴AG=BM=2（2-1）．例2 ．如图，P 为正方形ABCD 内一点，10PA PB ==，并且P 点到CD 边的距离也等于10，求正方形ABCD 的面积【解析】：过P 作EF AB ⊥于F 交DC 于E ．设PF x =，则10EF x =+，1(10)2BF x =+．由222PB PF BF =+． 可得：222110(10)4x x =++． 故6x =．216256ABCD S ==．例 3. 如图，E 、F 分别为正方形ABCD 的边BC 、CD 上的一点，AM EF ⊥，•垂足为M ，AM AB =，则有EF BE DF =+，为什么【解析】：要说明EF=BE+DF ，只需说明BE=EM ，DF=FM 即可，而连结AE 、AF ．只要能说明△ABE ≌△AME ，△ADF ≌△AMF 即可． 理由：连结AE 、AF ．由AB=AM ，AB ⊥BC ，AM ⊥EF ，AE 公用， ∴△ABE ≌△AME ． ∴BE=ME ．同理可得，△ADF ≌△AMF ．∴DF=MF ．∴EF=ME+MF=BE+DF ．例4．如下图E 、F 分别在正方形ABCD 的边BC 、CD 上，且45EAF ︒∠=，试说明EF BE DF =+。