受弯构件计算简化

第三章钢筋混凝土受弯构件正截面承载力计算受弯构件（bendingmember）是指截面上通常有弯矩和剪力共同作用而轴力可以忽视不计的构件。

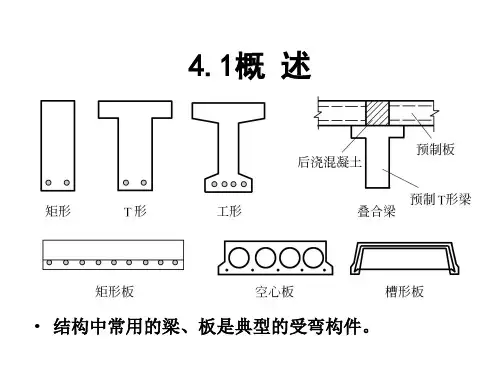
钢筋混凝土受弯构件的主要形式是板（Slab）和梁（beam）,它们是组成工程结构的基本构件，在桥梁工程中应用很广。

在荷载作用下，受弯构件的截面将承受弯矩M和V的作用。

因此设计受弯构件时，一般应满意下列两方面的要求：（1）由于弯矩M的作用，构件可能沿弯矩最大的截面发生破坏，当受弯构件沿弯矩最大的截面发生破坏时，破坏截面与构件轴线垂直，称为正截面破坏。

故需进行正截面承载力计算。

（2）由于弯矩M和剪力V的共同作用，构件可能沿剪力最大或弯矩和努力都较大的截面破坏，破坏截面与构件的轴线斜交，称为沿斜截面破坏，故需进行斜截面承载力计算。

为了保证梁正截面具有足够的承载力，在设计时除了适当的选用材料和截面尺寸外，必需在梁的受拉区配置足够数量的纵向钢筋，以承受因弯矩作用而产生的拉力；为了防止梁的斜截面破坏，必需在梁中设置肯定数量的箍筋和弯起钢筋，以承受由于剪力作用而产生的拉力。

第一节受弯构件的截面形式与构造一、钢筋混凝土板的构造板是在两个方向上（长、宽）尺度很大，而在另一方向上（厚度）尺寸相对较小的构件。

钢筋混凝土板可分为整体现浇板和预制板。

在施工场地现场搭支架、立模板、配置钢筋，然后就地浇筑混凝土的板称为整体现浇板。

通常这种板的截面宽度较大，在计算中常取单位宽度的矩形截面进行计算。

预制板是在预制厂和施工场地现场预先制好的板，板宽度一般掌握在Inl左右，由于施工条件好，预制板不仅能采纳矩形实心板，还能采纳矩形空心板，以减轻板的自重。

板的厚度h由截面上的最大弯矩和板的刚度要求打算，但是为了保证施工质量及耐久性的要求，《大路桥规》规定了各种板的最小厚度；行车道板厚度不小于IOOmm人行道板厚度，就地浇注的混凝土板不宜小于80mm,预制不宜小于60mm。

空心板桥的顶板和底板厚度，均不宜小于80mm。

一、受弯构件（一）在主平面内受弯的实腹式构件抗弯强度应符合下列规定1、翼缘板弯曲正应力满足下列要求：双向受弯的实腹式构件：f d ≥γ0(M y W y,eff +M z W z,eff )式中：γ0——结构重要性系数；M y 、M z ——计算截面的弯矩设计值；W y,eff 、W z,eff ——有效截面相对于y 轴和z 轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。

2、腹板剪应力应满足下列要求。

闭口截面腹板剪应力应按剪力流理论计算。

γ0τ≤f vd式中：γ0——结构重要性系数；τ——剪应力；f vd ——钢材的抗剪强度设计值。

3、平面内受弯实腹式构件腹板在正应力 σx 和剪应力 τ 共同作用时，应满足下列要求。

γ0√(σx f d )2+(τf vd)2≤1 式中：σx ——x 方向正应力；f d ——钢材的抗拉、抗压和抗弯强度设计值。

（二）受弯构件的整体稳定性应符合下列规定1、等截面实腹式受弯构件，应按下列规定验算整体稳定。

γ0(βm,yM y χLT,y M Rd,y +M z M Rd,z )≤1 γ0(M y M Rd,y +βm,z M z χLT,z M Rd,z)≤1 M Rd,y =W y,eff f dM Rd,z =W z,eff f dλLT,y =√W y,eff f y M cr,y ，λLT,z =√W z,eff f y M cr,z式中： M y 、M z ——构件最大弯矩；βm,y、βm,z——等效弯矩系数；χLT,y、χLT,z——M y和M z作用平面内的弯矩单独作用下，构件弯扭失稳模态的整体稳定折减系数；λ̅̅̅LT,y、λLT,z——弯扭相对长细比；W y,eff、W z,eff——有效截面相对于y轴和z轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。

M cr,y、M cr,z——M y和M z作用平面内的弯矩单独作用下，考虑约束影响的构件弯扭失稳模态的整体弯扭弹性屈曲弯矩，可采用有限元方法计算。

受弯构件挠度什么是受弯构件？受弯构件是一种力学结构，在受到外力作用下，会发生弯曲变形。

受弯构件的常见形式包括梁、悬臂梁、梁柱等。

在实际工程中，受弯构件被广泛应用于桥梁、建筑物的梁柱结构、机械设备等领域。

挠度的定义挠度是指受弯构件在受到外力作用下产生的弯曲变形的程度。

挠度可以用来描述受弯构件的柔度和稳定性。

通常情况下，挠度是指受弯构件中某一点相对于构件的中性轴的偏移距离。

在弹性阶段，受弯构件的挠度与外力大小呈线性关系；在超弹性阶段，挠度与外力之间的关系就变得复杂了。

有时挠度还可以作为受弯构件的设计指标之一，根据挠度的限制来确定构件的截面尺寸和材料。

受弯构件的挠度计算是结构力学中的一个重要问题。

在实际工程中，为了保证构件的安全和稳定，在设计和施工过程中需要进行挠度计算。

挠度的计算需要考虑受弯构件的材料性能、几何形状和外力作用等因素。

常见的挠度计算方法包括梁的直接分析法、基于力方法的挠度计算、基于位移法的挠度计算等。

其中，梁的直接分析法是最常用的挠度计算方法之一。

该方法通过对梁的受力进行平衡和力学分析，得到梁的弯矩方程，再通过积分求解得到梁的挠度分布。

这种方法计算简单，适用于遍及各种载荷和边界条件的梁的挠度计算。

对于不规则形状的受弯构件，基于力方法的挠度计算可以考虑构件的刚度分布，将构件分解为若干小段进行分析，再通过叠加原理得到构件的总挠度。

这种方法适用于复杂结构的挠度计算，并且可以考虑非线性材料的特性。

基于位移法的挠度计算是一种常见的数值计算方法。

该方法通过建立构件的位移方程，利用数值求解的方法得到构件的挠度分布。

这种方法适用于复杂结构和非线性问题，但是计算复杂度较高。

受弯构件的挠度受到多种因素的影响。

以下是一些常见的影响因素：1. 外力大小和作用形式外力的大小和作用形式对受弯构件的挠度有很大影响。

通常情况下，外力作用越大，受弯构件的挠度也就越大。

而外力的作用形式对挠度分布起到决定性作用，不同形式的外力会引起构件不同位置的最大挠度。

受弯构件斜截面受剪承载力计算一、有腹筋梁受剪承载力计算基本公式1．矩形、T形和Ⅰ形截面的一般受弯构件，斜截面受剪承载力计算公式为：VVc0.7ftbh01.25fyvAvh0(5-6)式中ft一混凝土抗拉强度设计值；b一构件的截面宽度，T形和Ⅰ形截面取腹板宽度；h0一截面的有效高度；fyv一箍筋的抗拉强度设计值；Av一配置在同一截面内箍筋各肢的全部截面面积，AvnAv1；n一在同一截面内箍筋的肢数；Av1一单肢箍筋的截面面积；一箍筋的间距。

2．集中荷载作用下的独立梁（包括作用多种荷载，且其中集中荷载对支座截面或节点边缘所产生的剪力值占总剪力值的75%以上的情况），斜截面受剪承载力按下式计算：VVcA1.75ftbh0fyvvh01.0(5-7)式中一剪跨比，可取a/h0，a为计算截面至支座截面或节点边缘的距离，计算截面取集中荷载作用点处的截面。

当小于1.5时，取1.5；当大于3.0时，取3.0。

独立梁是指不与楼板整浇的梁。

构件中箍筋的数量可以用箍筋配箍率v表示:vAvb(5-8)3．当梁内还配置弯起钢筋时，公式(5-4)中Vb0.8fyAbin式中(5-9)fy一纵筋抗拉强度设计值；Ab一同一弯起平面内弯起钢筋的截面面积；一斜截面上弯起钢筋的切线与构件纵向轴线的夹角，一般取45o，当梁较高时，可取60。

剪压破坏时，与斜裂缝相交的箍筋和弯起钢筋的拉应力一般都能达到屈服强度，但是拉应力可能不均匀。

为此，在弯起钢筋中考虑了应力不均匀系数，取为0.8。

另外，虽然纵筋的销栓作用对斜截面受剪承载力有一定的影响，但其在抵抗受剪破坏中所起的作用较小，所以斜截面受剪承载力计算中没有考虑纵筋的作用。

二、混凝土的受剪承载力可以抵抗斜截面的破坏，可不进行斜截面承载力计算，仅需按构造要求配置箍筋的条件oV0.7ftbh0或(5-10)V1.75ftbh01.0(5-11)三、计算公式的适用范围（上限和下限）l．截面限制条件当配箍特征值过大时，箍筋的抗拉强度不能发挥，梁的斜截面破坏将由剪压破坏转为斜压破坏，此时，梁沿斜截面的抗剪能力主要由混凝土的截面尺寸及混凝土的强度等级决定，而与配筋率无关。